基于線段模型的高速公路安全與流量關系研究

劉力瑋，馬博淵，王章宇，鄒睿航

（1.北京工商大學經濟學院，北京100048；2.北京工商大學計算機與信息工程學院，北京100048；3.北京工商大學材料與機械工程學院，北京100048）

1 模型理論

1.1 現實生活中的超車情形

現實中左駕右行的駕駛模式會受到多方面因素的影響，例如司機的駕駛習慣，汽車性能，道路性能。理想中，若所有車輛以相同速度行駛，則汽車行駛中不會發生超車，也不會被超車。但實際情況是每輛車的行駛速度并不相同，超車的發生次數也隨車流量密度的變化而不斷變化。

汽車是有空間和質量的物體，在行駛中會因駕駛不當發生碰撞。超車過程會受到多種因素的影響，如前后車間距，被超車輛對超車車輛的視線遮擋角度，超車車輛左側并道后在超車車輛后方是否存在也正在超越其他個體的車輛等。若單獨從微觀角度分析超車過程中的影響因素，諸多因素并不相互獨立，難以考慮所有影響因素來建立模型；若從某單一因素對超車過程的影響入手建立模型，又不能完整地體現超車過程中復雜的因素影響。所以在本文的左駕右行模型中，將車視為沒有質量，沒有空間的點。

超車的過程分為三個階段，第一階段，向左并道準備超車；第二階段，直線行駛，直到與被超車輛之間的距離符合行駛安全距離；第三階段，向右并道，回歸初始狀態。可以得出，超車過程是一個在時間與空間上都有變化的過程量。在模型中，車輛行駛都遵守不超車時在右側行駛的規則，只有在超車的時候才會往左邊移動一條車道完成超車。所以，模型將高速公路視為兩車道。

真實情況車道上的車輛有轎車、貨車、巴士等多種車輛。每種車在計算車流量時的數量不同，例如7 坐及以下轎車為1veh/h，拖掛貨車為3veh/h。模型中將所有的車輛都視為7 坐以下的轎車，即所有的個體車輛所占的車流量都為1veh/h。

1.2 模型整體思想

在模型中，不考慮超車過程中的變道時間，忽略變道過程中向左前行駛與右前行駛造成的相較于直線行駛距離的增加。將所有點放在一條線段上運動，每個點的運動速度恒定，總體的速度呈正態分布。當點之間發生一次重疊的時候，記為一次超車。點與點之間的重疊是瞬時的，當某一點與前一點重合之后，這兩個點的運動狀態不發生任何變化，保持兩個點原來的運動狀態繼續運動，然后計算當點的運行狀態處于穩定狀態下的重疊的次數。也就是說當高速公路上的車輛成均勻分布，車輛的速度程正態分布。

參考NS 模型與上文中提到的模型，發現左駕右行模型涉及正常行車、超車、自由通行狀態、無法自由通行狀態（堵車）。影響因素包含車流量、道路中車輛密度和行車速度，這些因素并不獨立。在一個模型中將這些并不相互獨立的變量同時考慮需要龐大的計算量，而且不能保證準確性。

通過何種建模方式，保證模型準確性，同時使各個因素之間的相關性影響減小到最小，是模型開發的理想結果。在此需要理解車輛遵守左駕右行模型時的超車模型，將車看做質點之后，這些點之間的超越不存在換道，只要有一次重疊就是發生一次超車。

2 普通超車模型實例

在模型建立初期，為了簡化模型，排除了一些變量因素。例如司機的駕駛習慣、車流量對汽車行駛速度的影響、汽車速度對車間距的影響、車間距與超車概率的關系。這些影響因素會在之后加入，完善模型，進而得到和現實情況比較接近，且為兩車道的一條高速公路的數據，并將這個數據帶入模型之中。

根據沈大高速公路的車流流量數據，在2004 年之前，沈大高速公路的最大承載能力為55 000veh/24h，最低承載能力22 000veh/24h。此處的承載能力是雙向行駛的承載能力，因此應該除以2，得到單向行駛的最高承載能力與最低承載能力。設計限速為50～120km/h。根據沈大高速公路的最大與最小承載能力，可以得到車輛放行的頻率0.01～0.32veh/s。

模型將所有車輛看成單位為1veh 的點，并且所有點在一條線段上運行。查閱資料后，未能找到其他與本模型相同假設的模型。

因此，在本文模型中采用仿真試驗的方法模擬一條高速公路中超車發生的次數。通過對照試驗的方法研究：

（1）高速公路限速上下限對汽車行駛實際情況造成的影響；

（2）高速公路平均行駛速度對汽車行駛實際情況造成的影響。

在設計“高速公路限速上下限對汽車行駛實際情況造成的影響”時，考慮到高速公路中所有車輛的行駛速度應該服從正態分布，根據期望速度與速度標準差可以憑借方差為界確定汽車速度的上下限。

2.1 同一正態分布下的車流量與超車次數的關系

通過對沈大高速公路車輛數量和行駛速度分析得出，二者之間服從以23.68m/s 為期望，以4.83m/s為標準差的正態分布，及X～N(23.68，4.832)。沈大高速公路不同車速及其數量關系如圖1所示。

根據上述的模型介紹，在線段起始端依照一定的流量拋出隨機速度的點，最后計量在一定時間內拋出的點在線段上碰撞次數，并以發生的碰撞次數來代替超車次數，最后進一步說明車流量與安全的權衡。

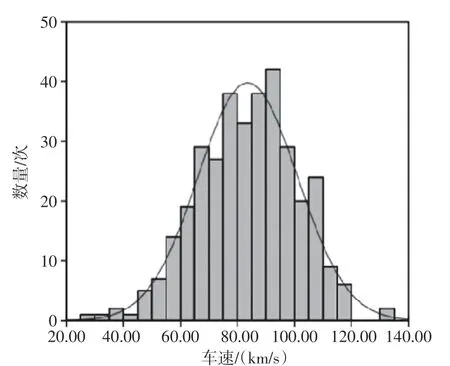
圖1 沈大高速公路不同車速及其數量直方圖

2.1.1 模型假設

本文模型采用以下假設：（1）把車輛視為質點；（2）沈大高速公路為一條直線，其全長為270km；（3）車輛在行駛過程中只有在超車時才會發生危險，即超車次數越多，發生危險的概率也就越大；（4）車輛放行速度是以在沈大高速公路測得的不同車速及其數量的數據擬合出的正態分布X～N(23.68，4.832)，同時是隨機拋出的。

2.1.2 模型方法

在線段的的起始點向線段中拋出一定流量的點（點單位為veh，流量單位為veh/h），待點在270 000m 的線段上均勻布滿后，開始計算在一定時間內的質點碰撞次數，且為了排除偶然因素，只計量均勻狀態下1h 的碰撞次數；在其他條件（線段長度、點拋出的正態分布、點均勻布滿時間及記錄時間）不變的情況下，改變拋出的車流量，以0.01作為車流量變動的最小單位；引入C++語言對上述過程進行編程計算，并根據得出的統計量使用MATLAB 擬合、修勻并給出相應表達式。通過引入C++語言對上述過程進行編程計算，得出的數據如表1和圖2所示。

表1 車流量與超車次數的關系

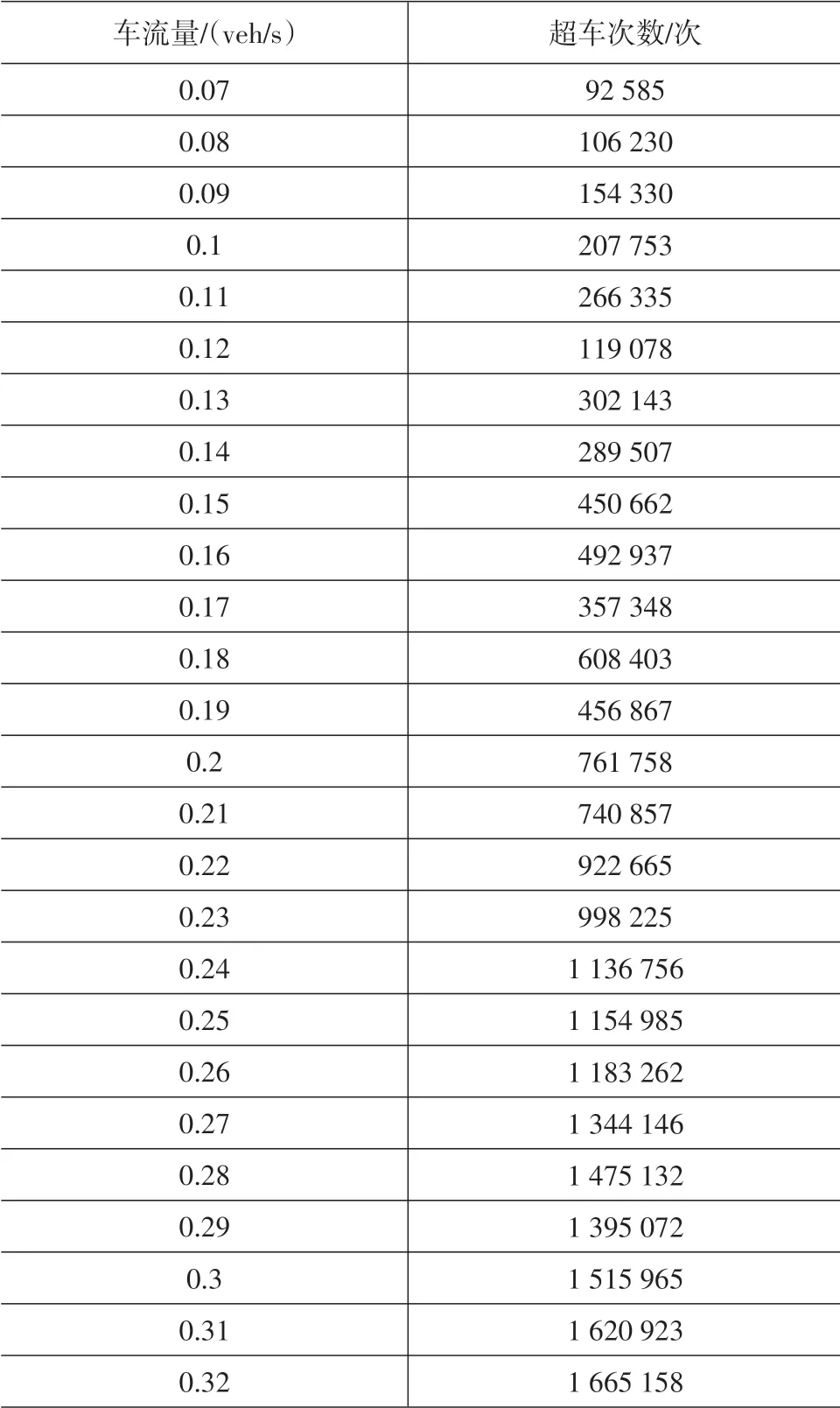
表1（續）

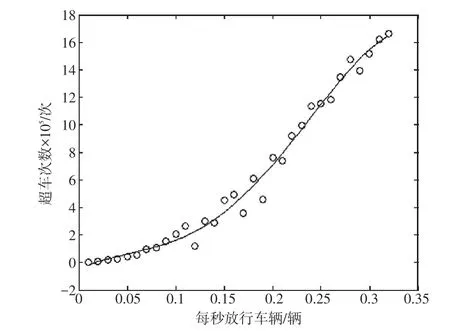
圖2 車流量與超車次數的關系

根據得出的統計量使用MATLAB 擬合、修勻，相應表達式為：

2.1.3 模型分析

在定量分析中，通過1h 的計量，可以清晰地看到隨著車流量的增加，超車次數在逐漸變大，但當車流量達到0.40veh/h 以后，超車次數變得穩定，也就是說在車流量達到0.40veh/h 后，曲線一改前一階段的變化規律，趨于穩定。此點過后，模擬的曲線性質發生了極大變化。

模型函數的二階導函數圖像如圖3所示。

圖3 車流量與超車次數函數的二階導數

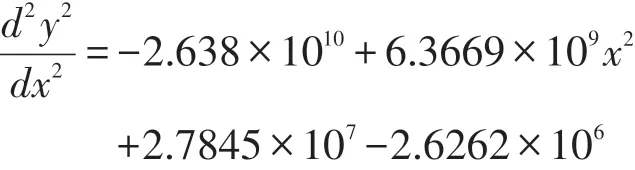
在二階導數中，如果x∈[ ]a,b,且時，在此區域函數為凹函數，如果x∈[b ,c],并且時，在此區域函數為凸函數，此時x=b 時為凹凸函數的臨界點，此二階導數的臨界點為：x1=0.02，x2=0.2403。在當車流量臨界點，原函數的凹凸性瞬間發生變化，就可以依據這兩個點確定最佳的車流量，即0.05veh/s和0.24veh/s（對原數據向下取證），但是車流量為0.02veh/h，道路的車流量極少相對0.24veh/s 時更加浪費資源，最后確定最佳車流量應確定為0.24veh/s。

現考慮車流量對超車率的影響，認為超車率越高潛在風險就越大。根據已有文獻，可知車流量達到500veh/h，即0.14veh/s時超車率最大，同時也是潛在風險最大的點的車流量，隨著車流量的邊緣化，超車率逐漸變小，同時潛在風險也在變小。當車流量為0.24veh/s 時，超車率為約為5%，潛在風險為最高時的5%/0.13%=38.46%，這樣認為是相對安全的。實際放行車輛與超車率的關系如圖4所示。

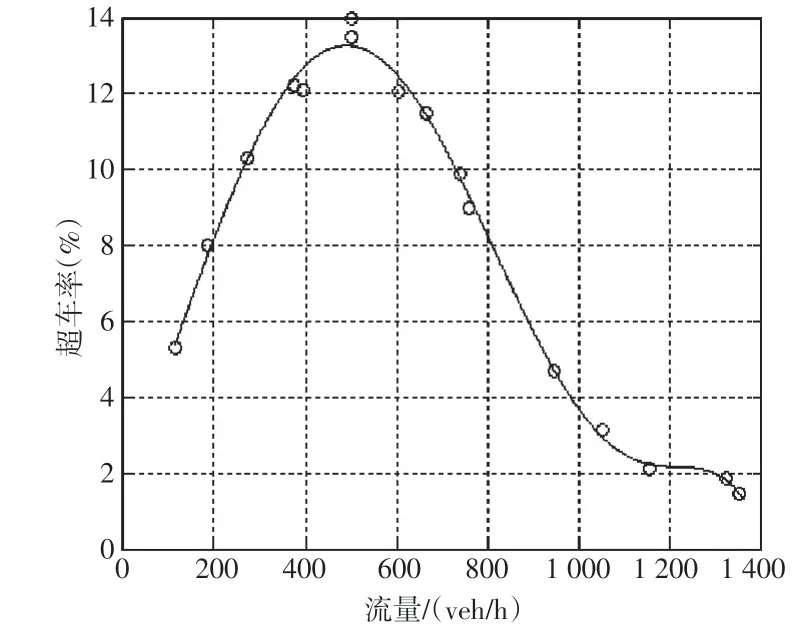
圖4 實際放行車輛與超車率的關系

2.1.4 模型結論

在安全和流量同時權衡時，可以車流量為0.24veh/s為基礎進行調整，調整量為0.01veh/s，即控制流量在0.23～0.25veh/s 時交通更有效率且有相對安全。

2.2 不同正態分布下的車流量與超車次數的關系

2.2.1 模型方法

為了研究速度上下限的控制對整個系統最佳放行量的影響，在上述模型的基礎上增加一個變量，即改變速度的期望值來實現改變所拋出質點速度的正態分布形式，依次為X～N(33.3,4.822)、X～N(27.6,4.822)、X～N(23.68,4.822)、X～N(19.4,[4.822)]和X～N(16.6，4.822) 。

同理，使用C++進行模擬，并根據得出的統計量使用MATLAB 擬合、修勻，不同正態分布下的放行車輛與超車次數的關系如圖5所示。

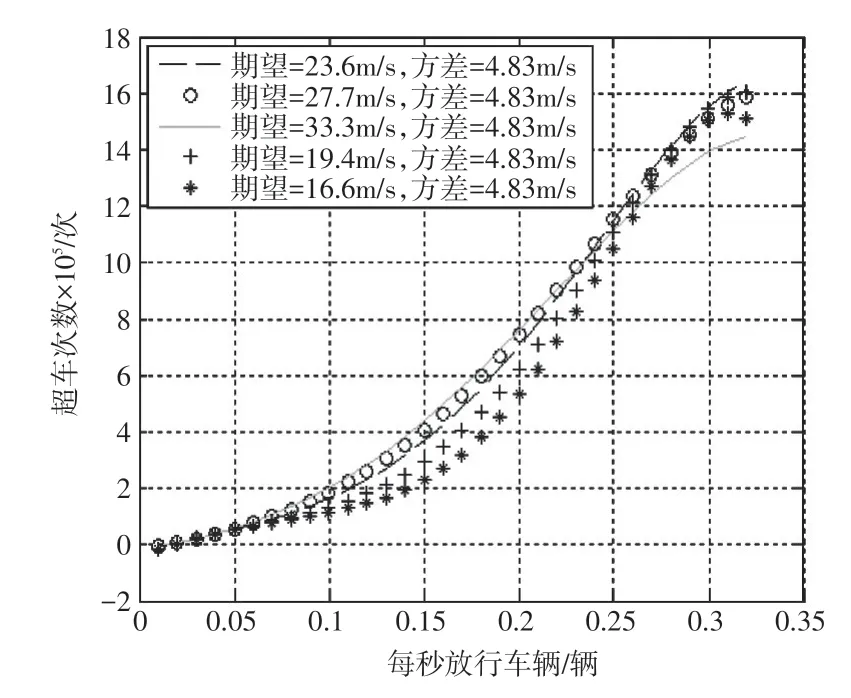
圖5 不同正態分布下的放行車輛與超車次數的關系

2.2.2 模型分析

不同的車速控制下，曲線的形狀并未發生巨大變化，依舊是先隨著車流量的增大，超車次數緩慢增大；再經歷一段快速走高的態勢；最后，均在0.4veh/s后達到平穩。

模型函數的二階導函數圖像如圖6所示。

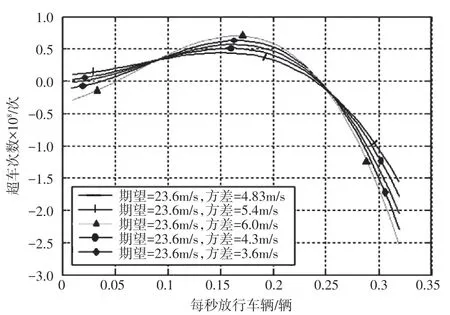
圖6 不同正態分布下的放行量與超車次數函數的二階導數

基于上述最佳通行量的選擇方法，X～N(33.3,4.832)、X～N(27.6,4.832)、X～N(23.68,4.832)、X～N(19.4,4.832)和X～N(16.6,4.832)的最佳通行流量依次為0.22veh/s、0.24veh/s、0.24veh/s、0.25veh/s 和0.25veh/s，所以行車速度的管制并沒有太多的改變超車次數，這樣就認為速度管制不會影響車流量。

考慮車流量和與超車率的關系：根據上述的文獻資料可以知道車流量為860veh/h，即0.24veh/s時安全性越高，所以取0.24veh/s為相對較安全的車流量，這樣就認為速度管制不會影響相對安全車流量。

2.2.3 模型結論

在安全和流量同時權衡時，可以以車流量為0.24veh/s為基礎進行調整，調整量為0.01veh/s。所以控制流量在0.23～0.25veh/s 時交通更有效率且有相對安全。這樣就得出：速度管制并沒有有效提高車流量和安全度。

3 智能交通的超車模型實例

在實際道路中，超車與否不僅僅取決于車速，還取決跟車距離，以及個人的駕駛超車意愿等因素，而整個道路系統中，若其中某一輛車以上某一因素改變，必會導致后面車輛產生連鎖反應，故不能簡單地靜態分析整個車道系統，同時由于動態分析會導致問題的連鎖反應，也不宜采用此方法。在此，試圖嘗試從微觀的角度考慮兩輛車之間的超車行為，進而引進單輛汽車的智能駕駛，以構建整個智能的駕駛系統。

假設微觀系統中，僅含兩輛汽車，分別為前面的汽車A和后面的汽車B，且均服從右側駕駛規則。首先由汽車B上的距離傳感器檢測出車A和車B 之間的距離，記為L，當L到達一個臨界超車距離Lo時，開始考慮前后車速，這時前后車的車速由速度傳感器測定，記前車車速為va，后車車速為vb，當va≥vb時，不考慮超車；但va＜vb時，才考慮從左側超車。此時的系統開始進一步計算超車加速度這個過程中設定汽車有一個最大加速度amax，當a＜amax時，開始超車。當然，這個過程中還需檢測A車的加速度aa，當aa＞0時，即前車處于加速階段，給B車系統一個反饋信號，不允許B車超車，這也符合的法律規定；當aa≤0 時，開始考慮從左側超車。這樣微觀智能汽車系統已經建成。對整體道路系統而言，系統是由很多無序的微觀系統構成，當微觀系統穩定時，智能道路系統也是穩定的，即此時道路系統可以正常運行。

4 結語

基于前兩個模型的分析可知，在保證安全的前提下要使效率達到最高，可以以車流量為0.24veh/s為基礎進行調整，調整量為0.01veh/s，即控制流量在0.23～0.25veh/s 時既可以使交通更有效率且有相對安全，同時速度管制并沒有有效提高車流量和安全度。綜上所述，在高速公路的匝道口日放行量每晝夜為39744～43200時既保證安全，又確保效率。

[1] 譚滿春，徐建閩.車輛換道控制策略及其靈敏度分析[J].系統工程學報，2006（2）：206-210.

[2] 姚世華，譚滿春.車輛換道與交通流多目標優化控制模型及算法[D].廣州：暨南大學，2008.

[3] 榮建. 超車模型在雙車道公路仿真系統中的應用研究[J].公路交通科技，2007（11）：136-139.

[4] 丁春雷.高速公路交通流數學模型與分析[D].天津：天津大學，2003.

[5] 閻瑩，王曉飛.高速公路斷面運行車速分布特征研究[J].中國安全科學學報，2008（7）：171-176.