基于空間約束的快速魯棒特征匹配優化

趙 燁蔣建國 洪日昌

(合肥工業大學計算機與信息學院 合肥 230009)

1 引言

基于特征的配準方法以其計算量較少、速度快等特點廣泛應用于機器視覺、圖像拼接、目標識別、3維重建、圖片旅游、視頻摘要等諸多領域[14]-。尤其以基于 Lowe[5,6]提出的尺度不變特征轉換 (Scale Invariant Feature Transform, SIFT)算法應用較為廣泛。SIFT算法將尺度不變特征子與梯度方向描述子相結合，具有圖像縮放、旋轉、光照和仿射不變性等優點。然而由于 SIFT描述子的維度較高導致計算過于復雜，難以滿足在對速度要求高的場景。為了降低計算復雜度，縮短匹配時間，隨后有很多研究人員提出了各種基于 SIFT 的改進算法。文獻[7]提出了采用主成分分析(Principal Component Analysis, PCA)的方法對 SIFT描述子進行降維的PCA-SIFT算法，其算法中PCA-SIFT描述子的維度可以降低到 20維，但是該描述子的通用性不如SIFT描述子，需要通過有代表性的圖像計算投影矩陣，并且在執行快速匹配時的精度也不如SIFT，不太滿足實際應用[8]。文獻[9]提出梯度位置方向直方圖 (Gradient Location Orientation Histogram,GLOH)算法，把SIFT中棋盤格狀的塊狀分區變成同心圓形的放射狀分區，再使用PCA降低維度。該算子的獨特性比 SIFT要好，但是計算更復雜。文獻[10]提出的快速魯棒特征(Speeded Up Robust Features, SURF)算法是一種快速的特征檢測和描述算法。該算法在特征點檢測和向量描述中巧妙地利用快速積分和箱式濾波，在繼承 SIFT算法對圖像縮放與亮度變化不敏感、抗干擾以及魯棒性強的同時，大幅加快了特征的提取速度，基于SURF特征配準已成為模式識別領域中的一個新的研究熱點。

但是SURF的匹配精度還不夠優良，得到的特征匹配點還存在一定數量的誤匹配。而SURF主要應用在圖像處理的前端，其配準精度直接影響到整個系統性能。為了進一步提高SURF匹配精度，文獻[11]提出了結合顏色和全局特征的 SURF特征算法，文獻[12]通過加權的方式把 SURF特征與局部顏色直方圖結合起來。鑒于視覺詞之間的幾何關系在圖像識別中起到重要作用，近來文獻[13]采用最佳尺度空間的選擇來提高匹配性能，雖然以上的改進算法在一定程度上提高了匹配精度，但由于計算過于復雜，時間消耗非常大。因此，在保證計算復雜度基本不變的要求下，如何提高SURF匹配精度仍然是尚待解決的問題。

在以往算法中，特征點之間的空間關系往往被忽略，這使得計算成本高昂。特征點間的空間關系很容易獲得，而且計算簡便易行，為此本文提出一種基于空間約束的 SURF特征匹配優化算法(SC-SURF)，通過選擇最優匹配點計算投影矩陣，同時利用最優匹配點構造參考坐標系產生空間信息表，二者結合起來對按匹配度加權的匹配點進行幾何核查，以提高匹配的高效性和有效性。

2 SURF特征點匹配

SURF算法利用最近鄰比率方法判斷匹配度，最近鄰比率算法就是使用最近鄰距離與次近鄰距離的比值作為兩幅圖像的相似性判定度量，當該比值在一定的閾值范圍內時則認定該特征點是匹配特征點。

距離比閾值是特征點之間建立匹配關系的紐帶。Lowe的實驗給出了距離比與概率密度分布曲線，如圖1所示。閾值越小，匹配點的正確概率越大，然而匹配點數越少；閾值越大，匹配點數越多，但匹配準確率越小。Lowe將距離比閾值設為0.8。本文在SURF特征點匹配中按照最近鄰比率對匹配點進行優先隊列實現。

通過上面方法對SURF特征點進行匹配，得到的匹配點仍然存在一定數量的誤匹配，為了提高匹配精度，需要對特征點進行二次匹配。

3 SURF特征點的二次匹配

3.1 幾何校驗方法

為了進一步提純和濾除誤匹配，一般采用幾何校驗來實現SURF特征點的二次匹配。應用最廣泛的幾何校驗方法是隨機抽樣一致性(RANSAC)算法[14]。它是一種在一組觀測數據集中估計模型參數的迭代方法，可以從數據樣本中準確擬合數學模型，然后采用隨機抽樣驗證去除噪聲點。但該方法的性能在外點較多的情況下將受到很大影響，而且計算復雜度高，得到的結果并不理想。所以SURF的幾何校驗策略需要一種更簡便有效的方法。為此本文提出利用簡化的 RANSAC算法結合空間約束策略來實現幾何校驗。

3.2 二次匹配優化策略

特征點間的空間關系很容易獲得，而且計算簡便易行，本文從SURF特征點之間的相對空間關系出發，以最優匹配點構造參考坐標生成空間約束矩陣，可以大大地簡化計算復雜度。同時選擇最優匹配點做為初始數據集進而簡化 RANSAC算法，最后二者結合起來通過正誤率分析實現幾何校驗。

3.2.1空間約束矩陣 SURF匹配點之間的空間位置信息可以用一個矩陣表示[15]，對于任意N個匹配點，第i個和第j個匹配點滿足關系，從而使得空間信息表M中元素取值如式(1)，式(2)所示。

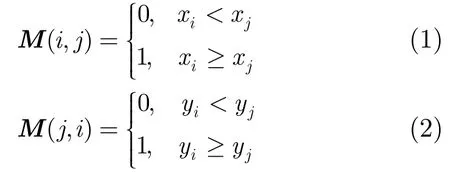
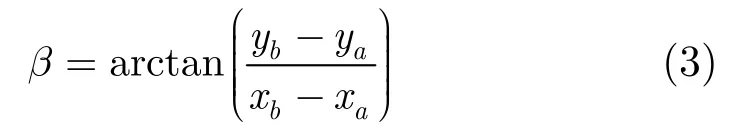
匹配點在新坐標系下的坐標為

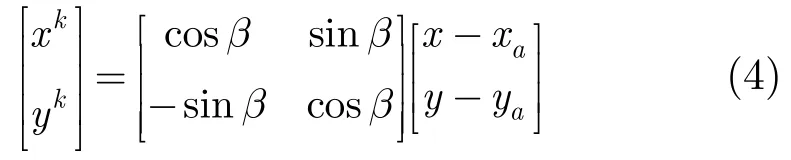
那么形成了3維空間約束矩陣M：

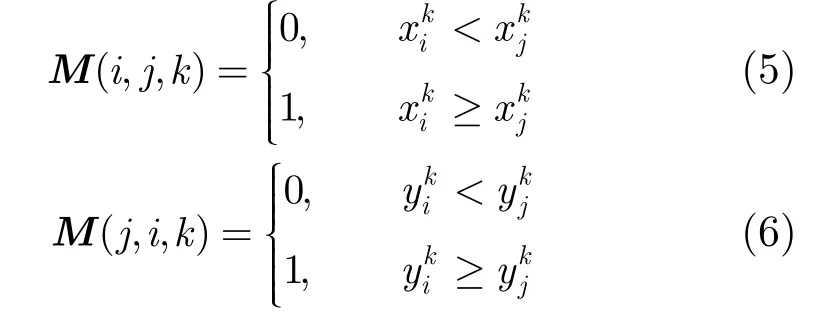
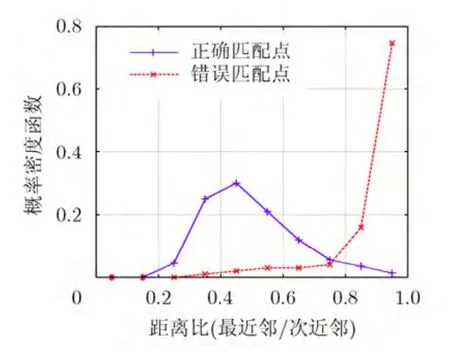
圖1 Lowe實驗的概率密度分布曲線

3.2.2簡化的RANSAC算法 RANSAC算法模型的參數估計是不斷通過內外點進行迭代計算和反復測試來完成的，初始模型參數是由隨機抽取樣本數據計算得到的，所以具有很大的不確定性，而初始參數的優劣直接決定著迭代次數和計算成本。本文簡化 RANSAC的方法是選擇少數最優匹配點作為初始樣本數據，這樣得到初始模型參數很接近真實值，可以通過設置盡量少的迭代次數來得到盡量真實的單應性矩陣參數，提高了計算效率。

本文選擇投影變換矩陣作為圖像變換模型，變換關系為

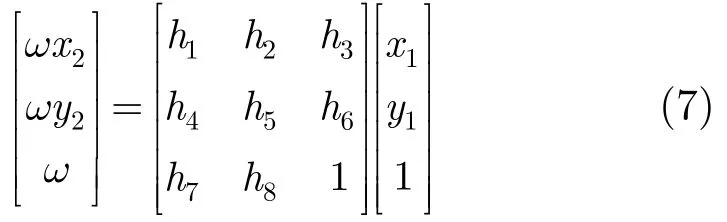
這是8個參數的投影變換，至少需要4個匹配對來生成，利用最小二乘法求解這8個參數。

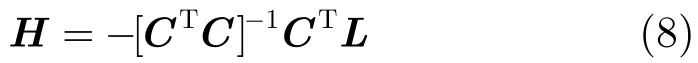
初始樣本數據數目n可按照式(9)確定：

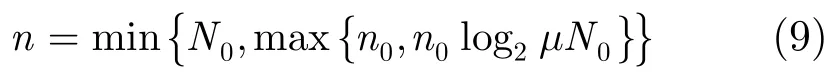
這里0N是一次匹配的匹配點數目，并且為樣本數目步長, μ為比例因數。

3.2.3空間幾何校驗 待配準的兩幅圖像根據相應的匹配對分別產生空間約束矩陣和，對和矩陣中的異值點進行統計，生成異值矩陣W：

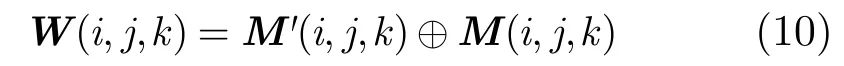
為了確保匹配精度，K值選擇應大于 2，但考慮到運算速度，K取值又不能過大，一般選擇K=3。最后得到特征點在空間約束矩陣下的錯誤率為id。

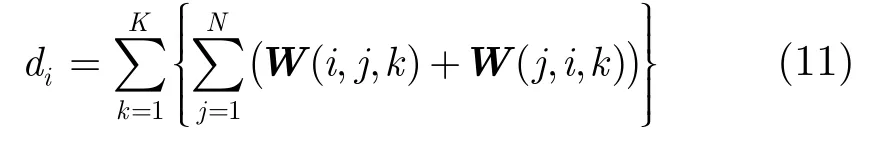
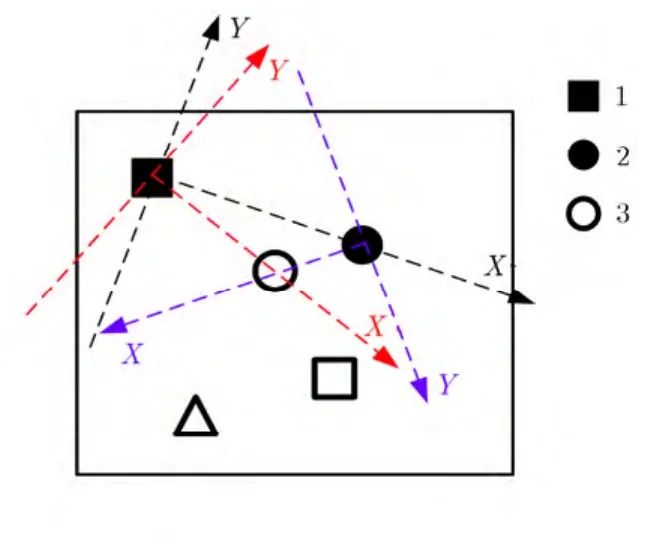
圖2 最優匹配點構成參考坐標系

設模型參數變換得到匹配點坐標值與實際坐標的距離值為jd，匹配點判別按照式(12)進行，由于透視變換矩陣僅為少數數據得出，不能保證求得最精確的結果，所以采用兩個約束條件相互補充。

式中α為比例因子, γ均為距離閾值。

4 實驗結果與分析

實驗的運行環境為 Genuine Intel(R) T2400(CPU), 1.83 GHz主頻，2 G內存的PC機。采用牛津大學的局部仿射變換數據集[16]，分別對SC-SURF算法與SIFT算法、SURF算法和帶有RANSAC校驗的SURF算法進行了對比實驗，匹配性能主要從匹配準確率(Precision)-召回率(Recall)和匹配速度兩個方面進行分析。鑒于準確率與召回率往往是矛盾的，因此本文又采用一個綜合指標加權調和平均(F-Measure)來幫助分析，加權調和平均是準確率和召回率加權調和平均：

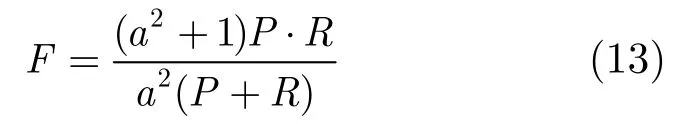
4.1 匹配性能測試實驗

對測試圖像在旋轉和尺度變化、視角變化、模糊變化、光照變化和JPEG壓縮等典型變換下進行了匹配實驗。其中SIFT的對比度閾值為0.02, S為3, O為7, SURF的描述子為64維，SC-SURF中的比例因子α根據多次測試實驗效果最佳時的取值為0.1，距離閾值。利用已知的單向性矩陣判斷匹配效果，最后將大量的實驗數據平均后，得到各種典型變換下各算法的查準率-召回率曲線和加權調和平均曲線，如圖 3～圖 7所示。在旋轉和尺度變換情況下，測試圖像角度旋轉3045°°～，尺度因子變化1～4倍。視角變化的測試圖片不僅有60°的旋轉視角，還有尺度和照度上的變化。從圖3，圖4的曲線中可以看出SC-SURF算法不論在尺度、旋轉變化還是視角變化下的匹配效果均好于其他算法。這是因為加入了空間約束和旋轉坐標，所以 SC-SURF具有更好的旋轉不變性和尺度不變性。

JPEG序列是利用標準的xv圖像瀏覽器通過改變圖像質量參數從40\%到2\%產生的，在抗JPEG壓縮方面，如圖7所示，SURF算法與RANSACSURF和 SC-SURF效果差異不大，都能很有效地抗壓縮變化。在以上各種圖像變換的情況下，SIFT的準確率指標較好，但其召回率較差，所以綜合指標加權調和平均性能較低，然而 DoG檢測子比Hessian檢測子可以提取更多的特征點數，一般SIFT檢測到的特征點數目是SURF檢測到的2～5倍。因此在對匹配速度要求不高的情況下，SIFT算法還是比SURF得到更廣泛的應用。

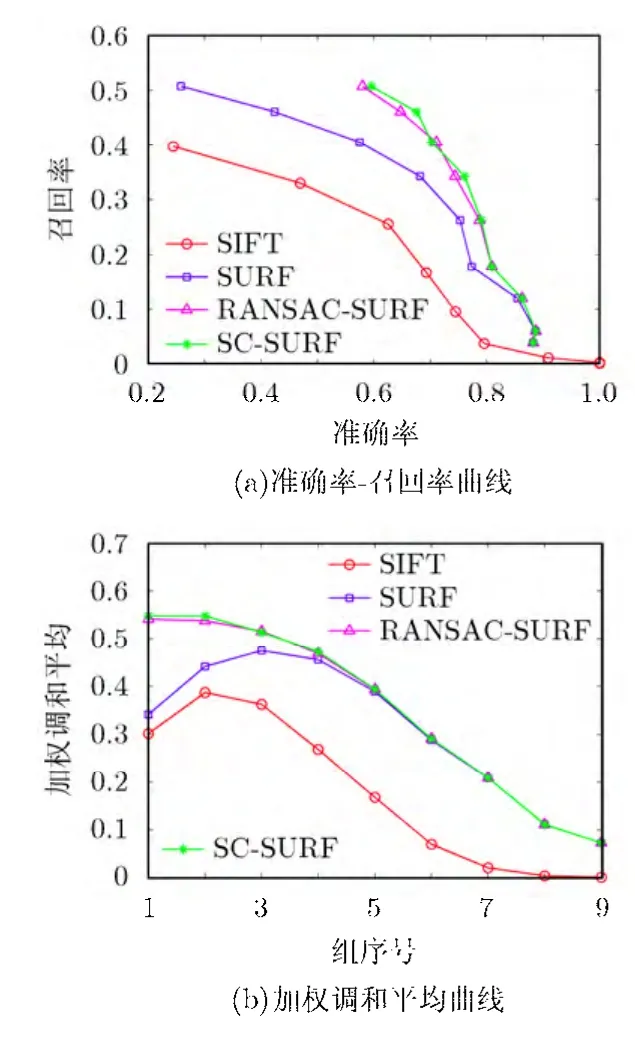
圖3 視角變化時各算法的性能比較

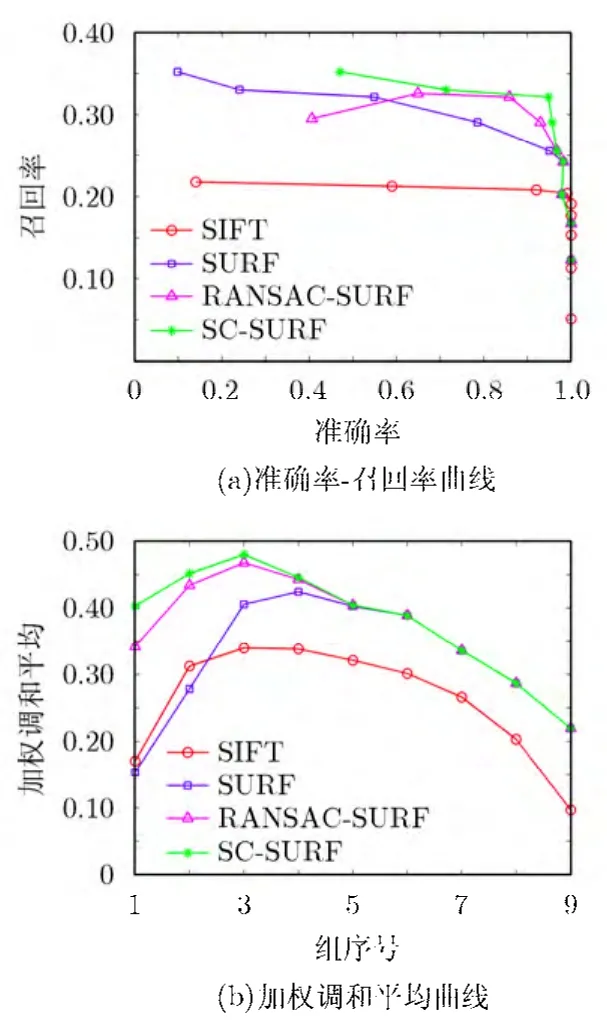
圖4 縮放旋轉變化時各算法的性能比較

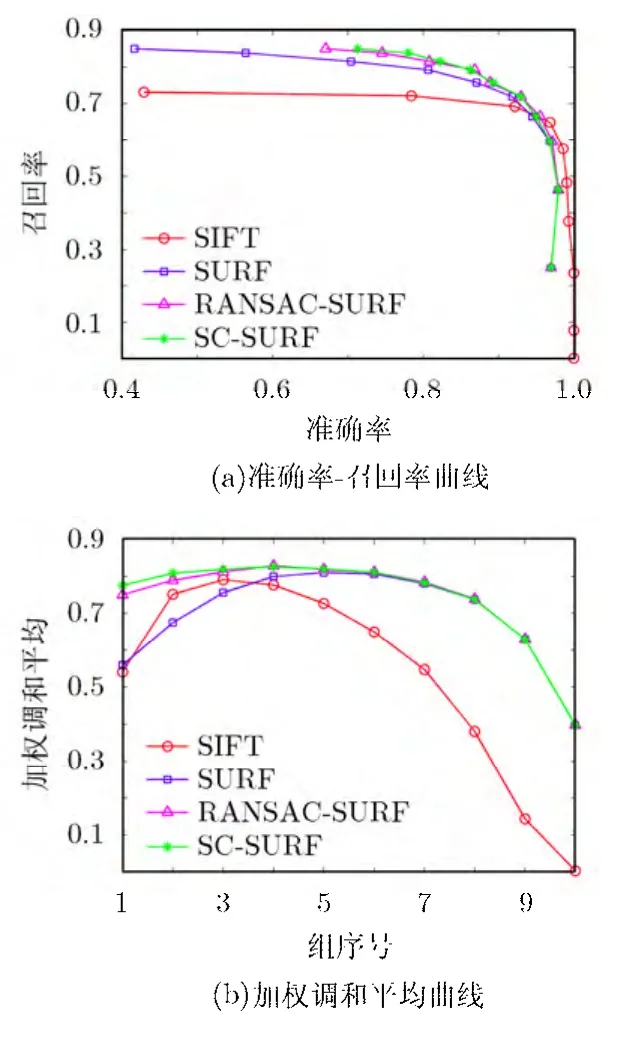
圖5 光照變化時各算法的性能比較

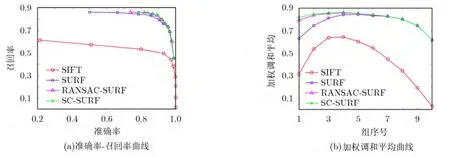
圖6 圖像模糊時各算法的性能比較

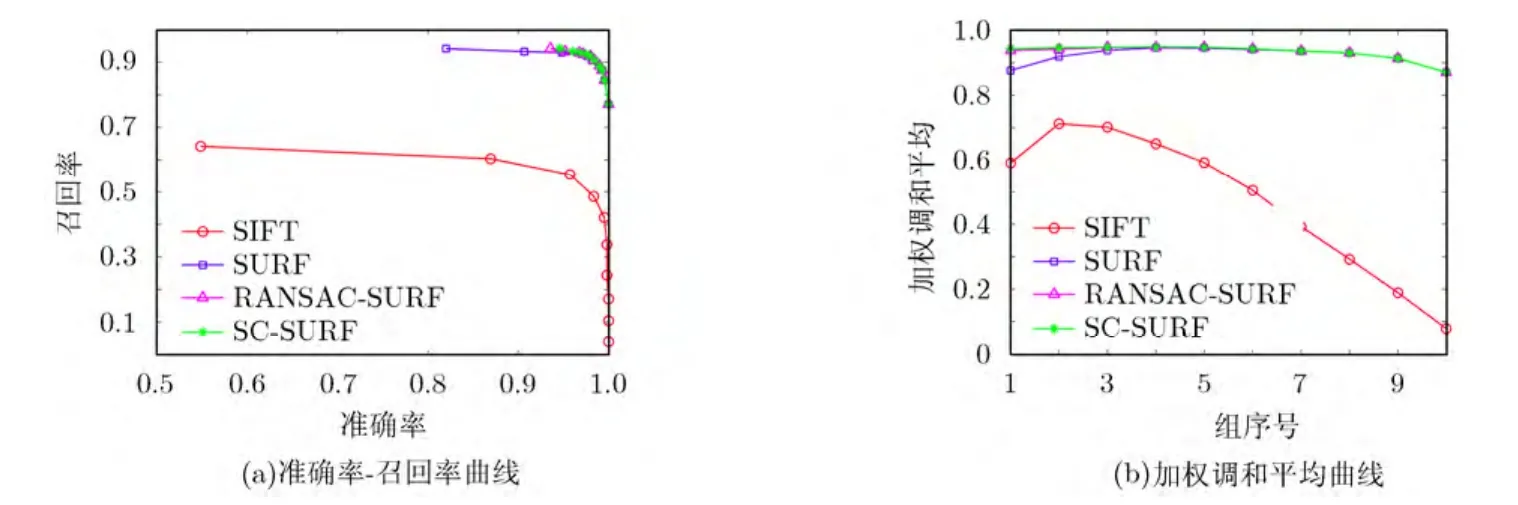
圖7 JPEG壓縮時各算法的性能比較

圖8給出了在視角變化下的匹配示例。測試圖像為Graf中img1與img2，距離比閾值為0.7，匹配結果為：SIFT的匹配點對是1230對，其中正確匹配對是1179對，配準率為0.95854。SURF的匹配點對是734對，其中正確匹配對是611對，配準率為0.8324。RANSAC-SURF的匹配點對是695對，其中正確匹配對是 611對，配準率為 0.8791。SCSURF的匹配點對是691對，其中正確匹配對是611對，配準率為 0.8842。綠色空心圓為正確匹配點，紅色十字形表示錯誤匹配點，可見 SIFT的配準率是最高的。

圖9所示是4種算法在近重復圖像下的匹配示例。

綜合上面的實驗結果，SC-SURF的匹配性能明顯優于其他算法，在匹配的有效性上相比于原始SURF有很大的改進。

4.2 匹配速度測試實驗

為了評估SC-SURF算法的計算復雜度，對這4種算法進行匹配速度測試。為了統一參數，SC-SURF算法與其余3種算法的距離比閾值均設為0.7，其余參數設置與上面實驗相同。在前面所述的運行環境下，樣本數目取100對，圖10給出了SIFT和SURF匹配時間的比較，圖11比較了RANSACSURF和SC-SURF的二次匹配時間。

由以上圖表可知，RANSAC-SURF在個別情況下的計算復雜度很高，這是由于樣本點中的外點過多，而 RANSAC要擬合的仿射矩陣總是受污點感染而達不到最優矩陣造成的。SIFT和 SURF的運行時間主要取決于檢測到特征點的數目。SIFT的運行時間遠遠大于SURF，大約是SURF的10～30倍。同時 SC-SURF的二次匹配運行速度相對RANSAC-SURF快3～100倍，在個別情況時能高達幾千倍，它的運行時間大約是SURF的2%左右，所以本文算法相對于原始SURF運行時間基本保持一致，但匹配精度大大提高。本文算法相對于RANSAC-SURF運行速度大幅度提高，同時匹配精度也比后者略好。

5 結束語

本文以SURF作為圖像的局部特征，構建了一種基于空間約束的 SURF特征點匹配的優化算法SC-SURF。為提高算法對各類變化圖像的適應性，在 BBF匹配搜索中按照最近鄰比率進行優先級排序，把匹配點間的空間約束關系和簡化的RANSAC算法結合起來進行幾何校驗，從而提高匹配精度和速度。通過對在圖像縮放和旋轉、光照、視角、模糊和壓縮等圖像典型變化下的實驗數據進行分析，SC-SURF算法在匹配準確率上明顯超過 SURF和SIFT算法，在匹配時間上控制在毫秒級，在保持與SURF運行時間幾乎不變情況下，大幅提高了匹配精度。同時在比 RANSAC-SURF的匹配精度略好的情況下，減少了計算復雜度。該算法在實際應用中仍存在很多待改進之處，由于對最優匹配點依賴性較強，因此如何進一步完善最優匹配的選擇條件，是下一步待研究的問題。

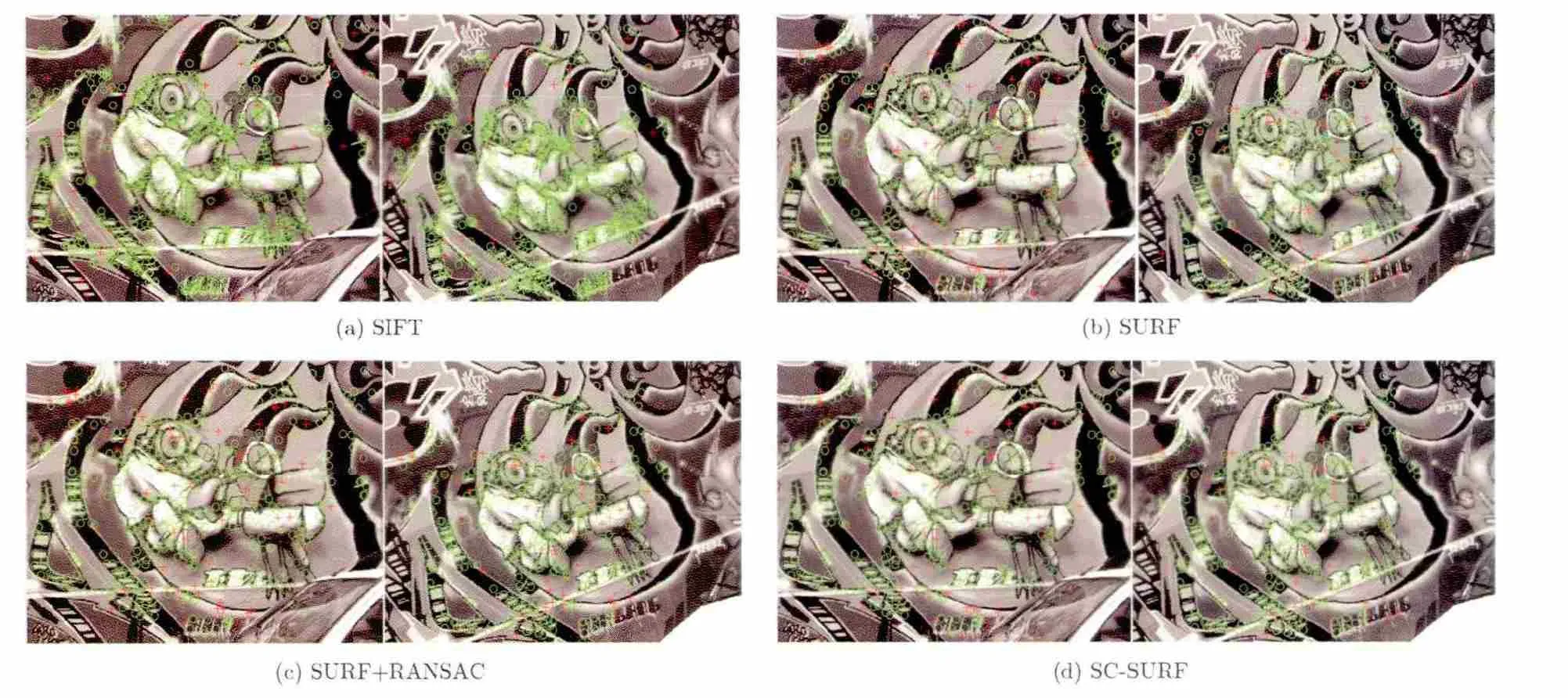
圖8 視角變化的匹配結果(綠色圓形符號表示正確匹配點，紅色十字形符號表示錯誤匹配點)

圖9 匹配實例(由上到下依次是SIFT, SURF, RANSAC-SURF和SC-SURF)

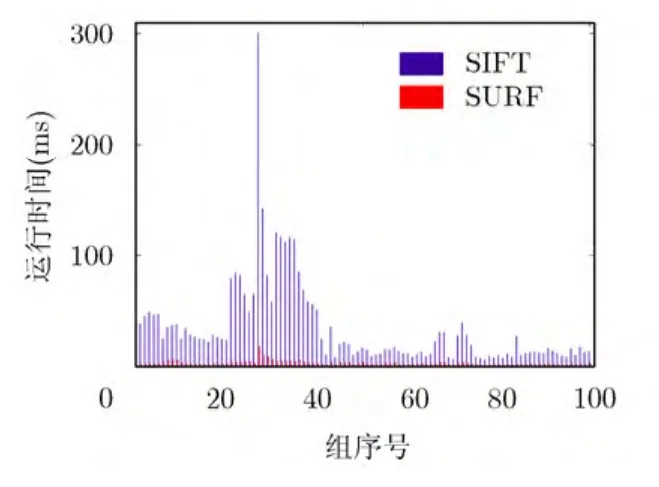
圖10 SURF與SIFT運行時間對比

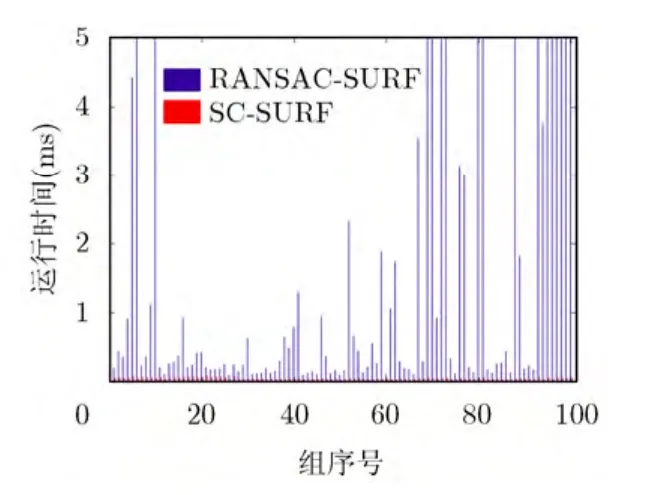
圖11 SC-SURF與RANSAC-SURF二次匹配運行時間對比

[1] Rudinac S, Larson M, and Hanjalic A. Learning crowdsourced user preferences for visual summarization of image collections[J]. IEEE Transactions on Multimedia, 2013,15(6): 1231-1243.

[2] Wang M, Ni B, Hua X, et al.. Assistive tagging: a survey of multimedia tagging with human-computer joint exploration[J]. ACM Computing Surveys, 2012, 44(4): 1-25.Conference on Computer Vision, Los Alamitos, 1999:1150-1157.

[6] Lowe D. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004,60(2): 91-110

[7] Ke Y and Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors[C]. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington D. C., 2004: 506-513.

[8] Juan L and Gwun O. A comparison of SIFT, PCA-SIFT and SURF [J]. International Journal of Image Processing, 2009,3(4): 143-152.

[9] Mikolajczyk K and Schmid C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630.

[10] Bay H, Ess A, Tuytelaars T, et al.. Speeded-Up Robust Features (SURF)[J]. International Journal on Computer Vision and Image Understanding, 2008, 110(3): 346-359.

[11] Yoon H, Chung H, and Hahn H. SURF Algorithm with color and global characteristics[C]. Proceedings of ICCAS-SICE International Joint Conference, Fukuoka, 2009: 183-187.

[12] Fan P, Men A, Chen M, et al.. Color-SURF: a SURF descriptor with local kernel color histograms [C]. Proceedings of IEEE International Conference on Network Infrastructure and Digit Content Proceedings, Beijing, 2009: 726-730.

[13] Ehsan S, Kanwal N, Clark A, et al.. An algorithm for the contextual adaption of SURF octave selection with good matching performance: best octaves [J]. IEEE Transactions on Image Processing, 2012, 21(1): 297-304.

[14] Fischler M and Bolles R. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the Association for Computing Machinery, 1981, 24(6):381-395.

[15] Zhou W, Lu Y, Li H, et al.. Spatial coding for large scale partial-duplicate web image search[C]. Proceedings of the 18th ACM the International Conference on Multimedia, New York, 2010: 25-29.

[16] The Oxford University: Affine Covariant Features Database of Oxford University[OL]. http://www.robots.ox.ac.uk,2012.4.