手臂延伸與抓取運(yùn)動(dòng)時(shí)間協(xié)調(diào)小腦控制模型設(shè)計(jì)
張少白張 政
(南京郵電大學(xué)計(jì)算機(jī)學(xué)院 南京 210033)
1 引言
構(gòu)建手臂運(yùn)動(dòng)平衡控制模型,是機(jī)器人學(xué)及控制科學(xué)所研究的一個(gè)重要的課題。 英國諾丁漢大學(xué)人工智能研究小組的教授Barbara Webb曾經(jīng)說[1]:“傳統(tǒng)的控制技術(shù)需要依賴精確的傳感和驅(qū)動(dòng)以及復(fù)雜的信息處理,這種技術(shù)已經(jīng)不再適合具有類似感覺運(yùn)動(dòng)系統(tǒng)的機(jī)器人。”基于這種認(rèn)識,模擬小腦神經(jīng)系統(tǒng)的結(jié)構(gòu)特征或功能特征,建立各種人工小腦或小腦模型,并將其應(yīng)用于機(jī)器人的運(yùn)動(dòng)控制,正逐漸成為控制科學(xué)、機(jī)器人學(xué)以及人工智能等學(xué)科的重要研究領(lǐng)域。
正因?yàn)榇耍疚脑谖墨I(xiàn)[2]中曾經(jīng)為手臂的定向運(yùn)動(dòng)構(gòu)建了一個(gè)小腦控制模型,用以解釋和控制手臂運(yùn)動(dòng)形式與手的預(yù)成型之間有關(guān)時(shí)間協(xié)調(diào)的問題。文獻(xiàn)中假定,運(yùn)動(dòng)規(guī)劃是在運(yùn)動(dòng)前區(qū)皮層(premotor cortex)中產(chǎn)生的;手臂運(yùn)動(dòng)軌跡以一種前饋的方式產(chǎn)生,除了初始階段,不需要考慮手臂的實(shí)際位置;其延伸軌跡與典型鐘形切向速度的分布一樣,都是平滑的,并以某種反饋的形式在手和目標(biāo)位置一直被監(jiān)測的過程中產(chǎn)生。
但是,手臂控制本身不過是一種利用手臂在各種任務(wù)中抓取目標(biāo)的手段,并不是一種目的。本文感興趣的是,在延伸和抓取過程中,手臂運(yùn)動(dòng)形式與手的預(yù)成型(preshape)之間的時(shí)間協(xié)調(diào)問題。針對這樣的問題,文獻(xiàn)[3]曾經(jīng)構(gòu)建了一種基于最小加加速度最優(yōu)標(biāo)準(zhǔn)的經(jīng)典控制模型。該模型能很好地解釋各種條件下手臂移動(dòng)以及手部預(yù)成型過程的運(yùn)動(dòng)學(xué)原理,包括目標(biāo)位置和角度大小的細(xì)微變化,其關(guān)鍵部分是狀態(tài)預(yù)測,并能對系統(tǒng)傳入與傳出時(shí)產(chǎn)生的延時(shí)進(jìn)行補(bǔ)償。
鑒于小腦在運(yùn)動(dòng)系統(tǒng)中獨(dú)特的結(jié)構(gòu)和連通性以及小腦內(nèi)模和逆模所起的作用,對于超前狀態(tài)學(xué)習(xí)和剩余時(shí)間預(yù)測這樣的問題來說,應(yīng)用小腦控制模型進(jìn)行類似的學(xué)習(xí)和控制是非常合適的。基于這樣的考慮,文獻(xiàn)[2]對文獻(xiàn)[3]Hoff -Arbib控制模型進(jìn)行了修改,并在1維空間范圍內(nèi),對小腦如何學(xué)習(xí)被嵌入系統(tǒng)的前向模型的問題進(jìn)行了深入探討。此外結(jié)合時(shí)延問題,文獻(xiàn)[2]還對小腦如何應(yīng)用對運(yùn)動(dòng)命令的解釋來預(yù)測手和手臂運(yùn)動(dòng)前區(qū)(premotor)的未來狀態(tài),因而獲得精確平滑的運(yùn)動(dòng)軌跡的過程做出了說明。
本文是文獻(xiàn)[2]的續(xù)篇,主要目的是探討2維空間中時(shí)間協(xié)調(diào)的相關(guān)問題。為了實(shí)現(xiàn)這個(gè)目的,本文對適用于2維空間的控制機(jī)制及小腦模型做了適當(dāng)調(diào)整和修改,并對軌跡規(guī)劃延遲狀態(tài)信息在最終目標(biāo)位置附近的過沖以及震蕩過程中的表現(xiàn)行為等問題進(jìn)行了充分討論。仿真結(jié)果表明,由文獻(xiàn)[3]的Hoff-Arbib模型所獲得的有關(guān)延伸與抓取運(yùn)動(dòng)的動(dòng)力學(xué)的一些關(guān)鍵特征,小腦控制模型也能實(shí)現(xiàn),有些性能甚至更好。通過訓(xùn)練和學(xué)習(xí),改進(jìn)后的模型在2維空間中能獲得更為精確平滑的運(yùn)動(dòng)軌跡。
2 Hoff -Arbib模型
如圖1(a)所示,在Hoff-Arbib 模型中,手和手臂單獨(dú)被控制。延伸和抓取之間的協(xié)調(diào)是通過確定抓取角度(aperture)的形成以及手臂延伸到目標(biāo)這兩項(xiàng)所需的時(shí)間,然后將兩者之間的最大值作為持續(xù)輸入信號來完成的。控制器由比例微分(Proportional-Derivative, PD)控制器構(gòu)成,如圖1(b)所示。
手臂控制規(guī)則為
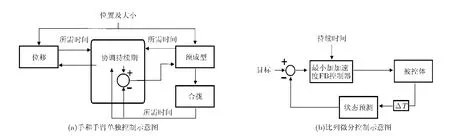
圖1 Hoff-Arbib模型示意圖

3 模型構(gòu)建
新的控制模型在 Hoff-Arbib模型的基礎(chǔ)上構(gòu)建,主要加入了用以學(xué)習(xí)被控體前向模型的小腦模塊以及剩余時(shí)間(Time-To-Go, TTG)預(yù)測部分,如圖2所示。將Hoff-Arbib模型復(fù)雜化的主要原因,是考慮到生物系統(tǒng)本身存在傳入和傳出延時(shí)問題。Hoff-Arbib模型中,這個(gè)問題是通過應(yīng)用系統(tǒng)解析前向模型來解決的。本文的任務(wù)就是要證明,小腦模塊通過訓(xùn)練也能獲得同樣的效果,甚至更好。依據(jù)文獻(xiàn)[4]所討論的結(jié)果,這個(gè)任務(wù)可以被很好地完成。
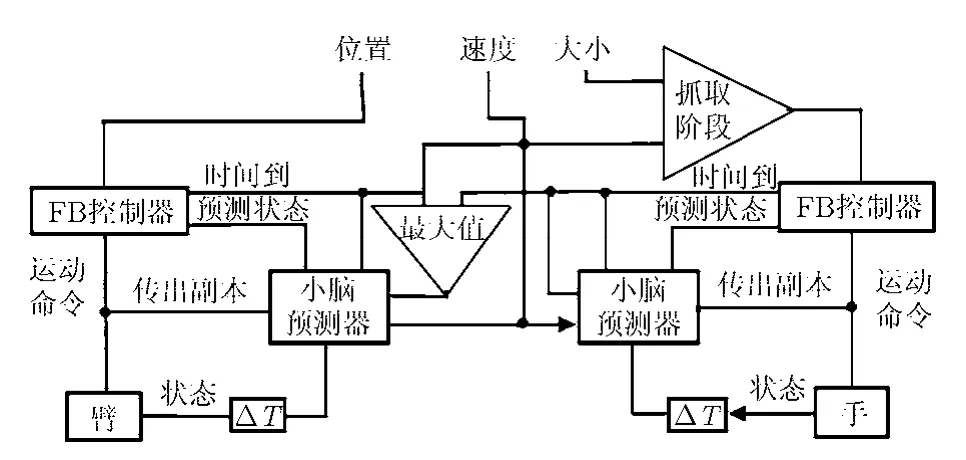
圖2 延伸和抓取時(shí)間協(xié)調(diào)模型示意圖
本文將系統(tǒng)對模型的訓(xùn)練分為了兩種形式。第1種(簡稱模型1)是用距離和角度兩個(gè)標(biāo)量來表示手臂延伸和抓取角度的變化;而第2種(模型2)則是對第1種形式的擴(kuò)展,方法是應(yīng)用雙關(guān)節(jié)平面手臂取代模型1中的位置標(biāo)量,也就是將1維距離訓(xùn)練變換為笛卡爾空間中的多維運(yùn)動(dòng)(方向和距離)訓(xùn)練,從而增加了對系統(tǒng)復(fù)雜性和實(shí)用性的評價(jià)標(biāo)準(zhǔn)。
3.1 小腦模塊的構(gòu)建
根據(jù)對各種小腦模型的抽象,本文在文獻(xiàn)[5]中構(gòu)建了一種通用小腦模型。本文嘗試將此通用小腦模型應(yīng)用于上述系統(tǒng)模型的兩種形式之中。具體來說,對模型1而言,子系統(tǒng)包括抓取和移動(dòng)距離(位置)兩個(gè)部分;對模型2,移動(dòng)距離子系統(tǒng)又被分解為單獨(dú)的肩和肘兩個(gè)部分。并且,這些子系統(tǒng)都有兩個(gè)輸出,每一個(gè)輸出都用來預(yù)測系統(tǒng)當(dāng)前狀態(tài)的位置和速度。
對本文模型來說,當(dāng)軌跡在笛卡爾空間中孕育時(shí),其輸出就是對關(guān)節(jié)間手臂狀態(tài)(與到達(dá)下橄欖細(xì)胞(Inferior Olivary, IO)的輸入信號一致)的評估值,這與文獻(xiàn)[6]的敘述是一致的。依據(jù)現(xiàn)代生物學(xué)的觀點(diǎn),頂骨皮質(zhì)(parietal cortex)與視覺有關(guān),手部動(dòng)作是靠頂骨皮質(zhì)有關(guān)視覺的組織來引導(dǎo)的,尤其在與目標(biāo)空間特性相匹配的動(dòng)作過程中更是如此[7]。大腦皮質(zhì)區(qū)域的信息通過腦橋核(pontine nucleus)映射到小腦皮質(zhì)。小腦皮質(zhì)則通過楔小腦束(cuneocerebellar tract)接收肢體當(dāng)前狀態(tài)的相關(guān)信息。
依據(jù)此觀點(diǎn),本文借鑒文獻(xiàn)[8]論述的方法,在具體連接時(shí),模型利用小腦模塊接收作為苔蘚纖維(Mossy Fiber, MF)傳入信號的5組群碼(population coding)輸入,這些信號分別來自不同的子系統(tǒng)。其中,3個(gè)與代表脊髓傳入信號的延時(shí)狀態(tài)(位置,速度,加速度)相對應(yīng),一個(gè)表示目標(biāo)值與當(dāng)前位置之間的位置差,還有一個(gè)則表示當(dāng)前運(yùn)動(dòng)命令的傳出副本。模塊結(jié)構(gòu)參見圖3,具體構(gòu)建方法參見文獻(xiàn)[9]。
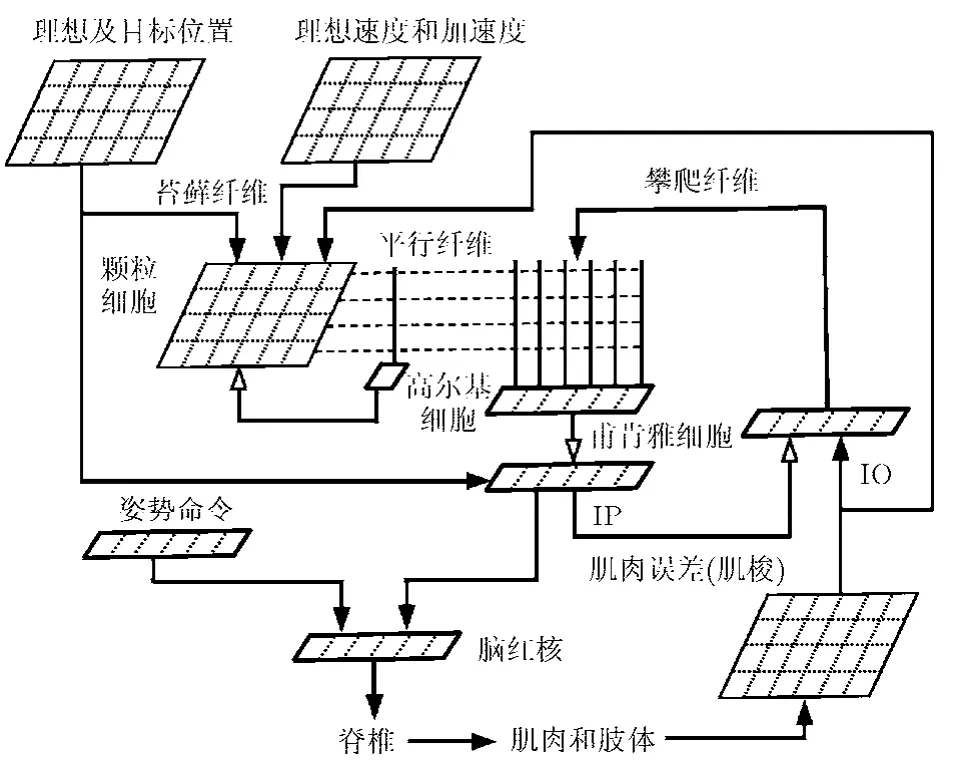
圖3 具有輸入輸出連接的小腦神經(jīng)系統(tǒng)
除此之外,模塊還接收先前產(chǎn)生的 TTG預(yù)測信息,抓取和手臂移動(dòng)子系統(tǒng)各有一個(gè),并且將MF作為一個(gè) 17×5的陣列來模擬。其中,每一行向量對特定的輸入變量進(jìn)行編碼。向量中的每個(gè)元素針對該變量都被調(diào)整到某個(gè)不同的值,以便形成群編碼。
行向量中元素i的活度(activation)iY可以定義為
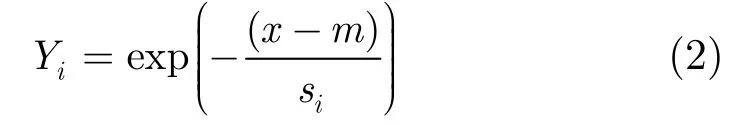
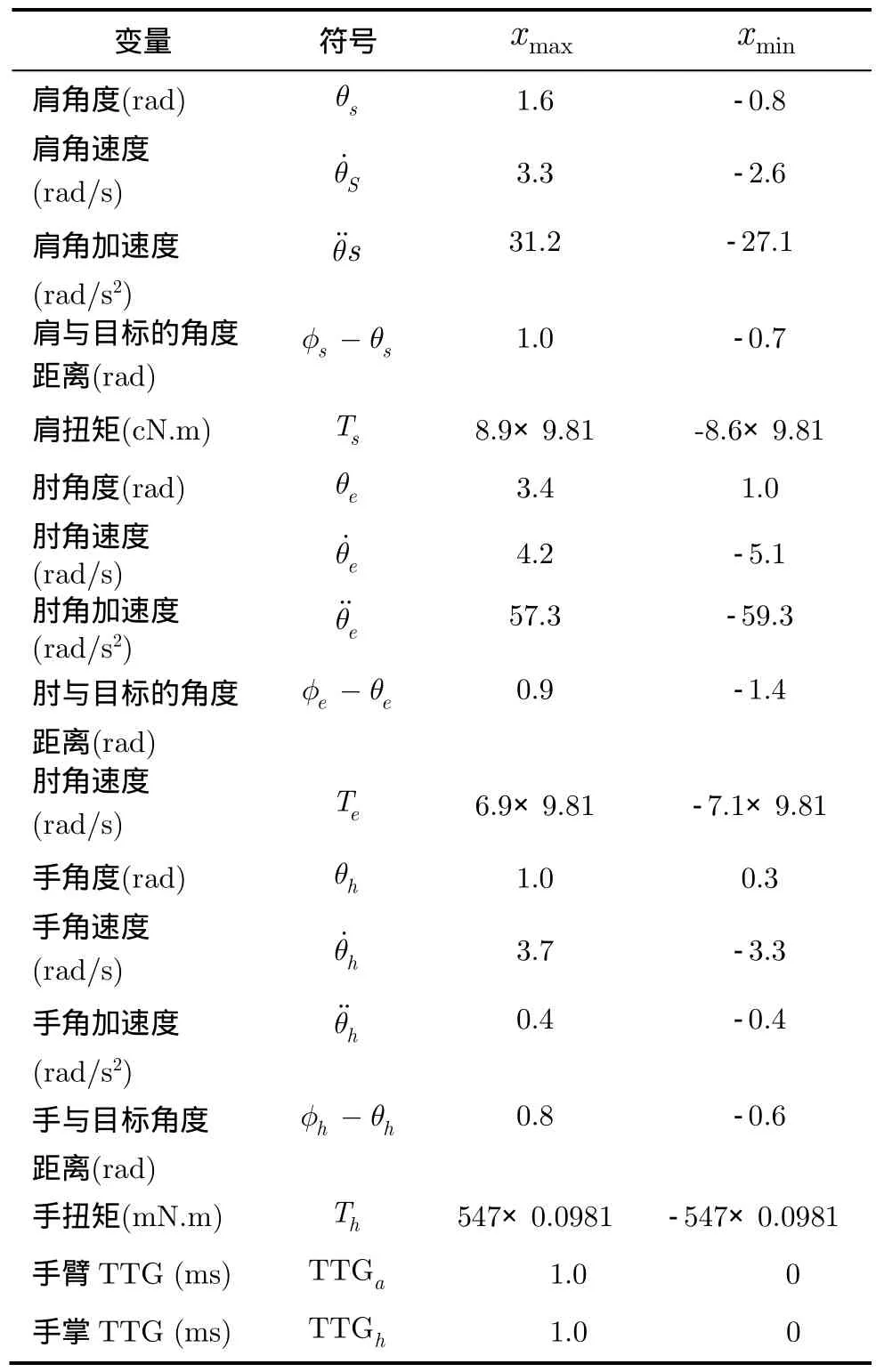
表1 用于群編碼方案的苔蘚纖維輸入?yún)?shù)表
另外如文獻(xiàn)[5]所述,隨機(jī)選擇的苔蘚纖維(MF)以及高爾基細(xì)胞(GolgI cell, GI)與顆粒細(xì)胞(Granule Cells, GC)的突觸一起,伴隨實(shí)時(shí)輸出,作為漏積分被建模。并且,這些實(shí)時(shí)輸出是作為膜電位的 sigmoidal 函數(shù)來計(jì)算的,用以表示細(xì)胞的瞬時(shí)激發(fā)率。
小腦模塊的構(gòu)建是本文的核心,但鑒于本文已經(jīng)在文獻(xiàn)[2,5,9]中對小腦模塊的構(gòu)建方法有過詳細(xì)敘述,在此只是對適用于本控制模型2維空間的特殊問題和方法進(jìn)行介紹,其它不再贅述。
3.2 學(xué)習(xí)規(guī)則
仿真過程中,下橄欖(IO)負(fù)責(zé)驅(qū)動(dòng)手部調(diào)節(jié)信號,每個(gè)IO細(xì)胞接收來自核細(xì)胞NUC抑制信息的輸入信號。因?yàn)楹思?xì)胞的興奮抑制與浦肯雅細(xì)胞(Purkinje Cell, PC)有關(guān),所以映射的效果可以通過修正pfw 即平行纖維-浦肯雅細(xì)胞(PF-PC)突觸的權(quán)值來實(shí)現(xiàn)。模型應(yīng)用文獻(xiàn)[5]中所述的學(xué)習(xí)規(guī)則更新PF-PC突觸的權(quán)值。
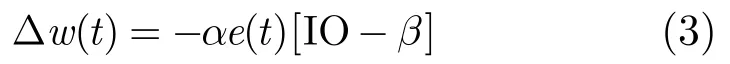
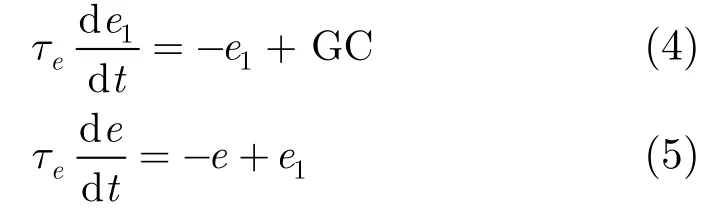
式中,GC(Granular Cell)為顆粒細(xì)胞活度,。微分方程的動(dòng)態(tài)特性使得顆粒細(xì)胞(GC)的輸入變得平滑,且不必與延遲信號精確匹配,其收斂性文獻(xiàn)[6]中已有證明。
3.3 控制系統(tǒng)
為了適用于2維空間的應(yīng)用,模型的控制系統(tǒng)較文獻(xiàn)[2]做了一些調(diào)整,設(shè)計(jì)為靜態(tài)逆與動(dòng)態(tài)逆相結(jié)合的方式(圖4),概念上類似于Kawato的并行分層控制方案[10]。其控制原則是,靜態(tài)逆模塊ISM(Inverse Static Module)的學(xué)習(xí)取決于手臂姿勢的動(dòng)態(tài)逆(如引力項(xiàng)),而動(dòng)態(tài)逆模塊 IDM(Inverse Dynamic Module)的學(xué)習(xí)則取決于關(guān)節(jié)的角速度。
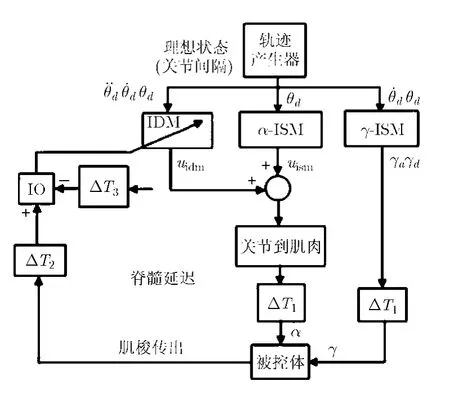
圖4 控制系統(tǒng)簡化示意圖
仿真過程中,ISM(其輸出為簡單函數(shù))以脫機(jī)查找表的形式被執(zhí)行。IDM則作為神經(jīng)系統(tǒng)的小腦模塊被實(shí)現(xiàn),具有生物學(xué)意義上的實(shí)時(shí)學(xué)習(xí)功能。
4 2維空間訓(xùn)練和學(xué)習(xí)相關(guān)問題的確定
4.1 手部抓取模塊
Hoff-Arbib 模型中,將與物體S尺寸有關(guān)的最大角度(maximum aperture)定義為+0.4,其形成時(shí)間與移動(dòng)相位的大小相一致,并使物體最終被握住的時(shí)間大約是200 ms的常數(shù)值。基于這樣的數(shù)據(jù),模型抓取過程處理模塊是作為單獨(dú)的判定框來執(zhí)行的。此判定框?qū)⑤斎胱鳛槲灰瓶刂频腡TG評估值,如果輸入大于200 ms,手部控制器的目標(biāo)值將被設(shè)置為maxa 。以此協(xié)調(diào)手臂運(yùn)動(dòng)與手預(yù)成型(preshape)之間的時(shí)間,以便臨近終點(diǎn)時(shí),形成與目標(biāo)形狀相匹配的封閉狀態(tài)。
4.2 2維空間訓(xùn)練過程
訓(xùn)練過程大致如下:首先,基于2 維視覺信息確定目標(biāo)對象的形狀、方向位置、距離和大小;其次,將相關(guān)信息提供給模型中的分布式執(zhí)行機(jī)構(gòu),分別確定手臂移動(dòng)的大致時(shí)間以及手部預(yù)成形時(shí)間;最后,在移動(dòng)及抓握過程中,需要對手臂延伸和手部抓取運(yùn)動(dòng)予以協(xié)調(diào)。這項(xiàng)工作可以通過比較抓握角度的形成時(shí)間以及手臂延伸到目標(biāo)所需的時(shí)間,從而將兩項(xiàng)時(shí)間中的最大值作為持續(xù)輸入信號來完成。
4.3 訓(xùn)練和學(xué)習(xí)方法
本文應(yīng)用文獻(xiàn)[9]所描述的雙關(guān)節(jié)平面手臂作為本文新控制模型仿真中的位置標(biāo)量。在手臂延伸至抓取過程中,抓取對象的距離、大小和方向非預(yù)期性變化,在擾動(dòng)實(shí)驗(yàn)中,將實(shí)驗(yàn)輸出數(shù)據(jù)與Hoff-Arbib模型的人手實(shí)驗(yàn)數(shù)據(jù)加以對比,從而可以獲得期望結(jié)果。
模型訓(xùn)練期間,總共要做2000次正常的手臂移動(dòng)延伸和抓取動(dòng)作,目標(biāo)直徑大小、對象距離以及持續(xù)時(shí)間分別在2~8 cm, 15~30 cm以及200~400 ms之間隨機(jī)選擇。特別需要加以關(guān)注的是TTG信號,如果沒有這個(gè)信號,手臂延伸和手部預(yù)成型的控制就沒有統(tǒng)一的終止信息,也就無法保證二者的統(tǒng)一狀態(tài),從而無法獲得預(yù)期效果。
5 仿真
5.1 不同速度的仿真
圖5是關(guān)于速度的訓(xùn)練仿真。圖中的每個(gè)分圖表示了3種不同速度下手腕速度(圖5 (a))、抓握角度(圖5 (b))、手腕加速度(圖5 (c))和抓握角速度(圖5 (d))的變化情況。
圖中的GO標(biāo)志(術(shù)語“GO Signal”中GO表示啟動(dòng)的意思。這里的GO是一種習(xí)慣性定義,沒有特殊意義)是一個(gè)關(guān)于運(yùn)動(dòng)速度的比例因子,涉及3種不同運(yùn)動(dòng)速度下有關(guān)精確抓握任務(wù)中統(tǒng)計(jì)得來的相關(guān)數(shù)據(jù)。仿真中,本文將速度初步分為3個(gè)等級,即GO=15表示低速運(yùn)動(dòng)所對應(yīng)的軌跡,GO=25對應(yīng)于高速運(yùn)動(dòng),而GO=20則是對應(yīng)上述兩者之間的軌跡。隨著仿真復(fù)雜度的增加,GO標(biāo)志可以劃分的更為細(xì)致一些。
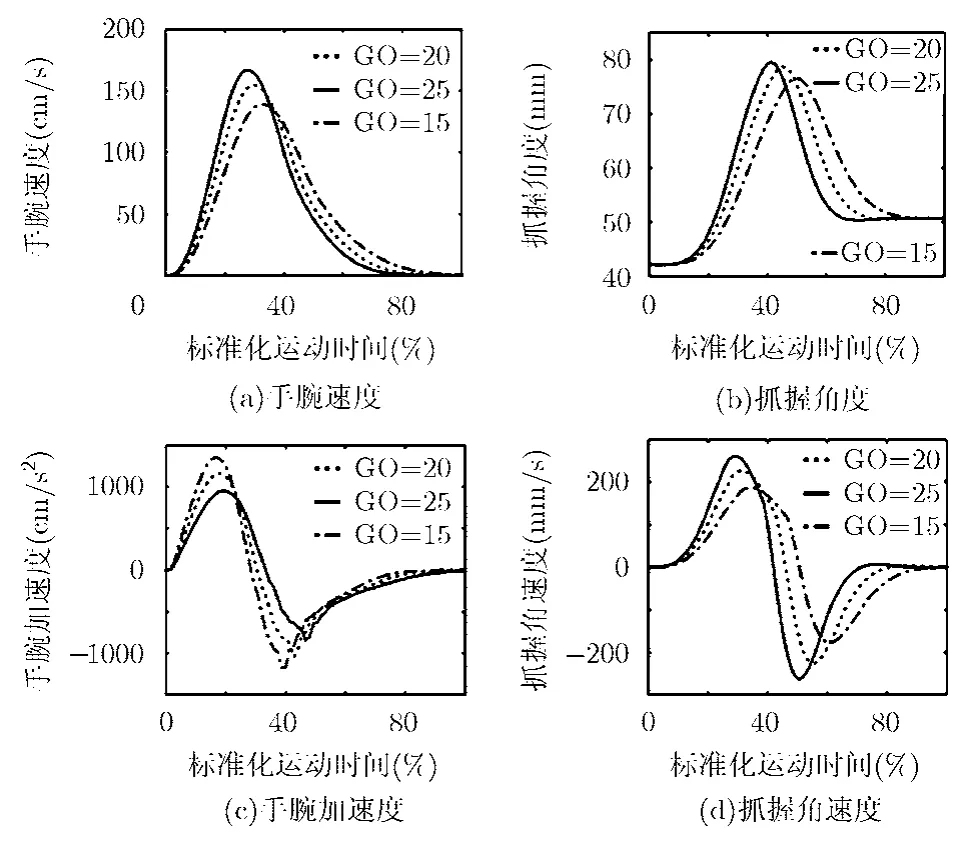
圖5 3種速度下移動(dòng)和抓握運(yùn)動(dòng)的動(dòng)力學(xué)軌跡示意
由結(jié)果可見,隨著手臂移動(dòng)速度的增加,最大抓握角度也會(huì)隨之增加。因此,由延伸和抓握運(yùn)動(dòng)所共享的GO標(biāo)志信號(即人手動(dòng)力學(xué)特征),模型不需要在兩種運(yùn)動(dòng)之間傳遞任何明確信息就可以獲得,這是本文構(gòu)建的小腦控制模型所具有的一個(gè)重要特征。
5.2 正常和變異抓握仿真
第5.1節(jié)討論了不同移動(dòng)速度會(huì)對最大抓握角度產(chǎn)生影響,那么影響手的張合度的因素又有哪些呢?文獻(xiàn)[11]應(yīng)用Hoff-Arbib 控制模型曾做過一個(gè)實(shí)驗(yàn),在實(shí)驗(yàn)中使用了兩種不同的抓握方法,即正常抓握(normal grasp)和變異抓握(altered grasp)。正常抓握開始時(shí)手指是放松的,抓握角度近似為零,而變異抓握開始時(shí)手指最大限度地張開。實(shí)驗(yàn)結(jié)果表明,對于變異抓握,初始角度還原之后,手指會(huì)有一個(gè)相對較小的重新張開的過程,有時(shí)甚至還會(huì)暫時(shí)停頓(速度軌跡為零),但最終都會(huì)處于封閉狀態(tài)。這表明在延伸-抓握過程中,手的形狀會(huì)有一個(gè)自然趨向封閉的過程,都會(huì)對手的張合度產(chǎn)生影響。仿此,本文應(yīng)用小腦控制模型也做了一個(gè)類似的實(shí)驗(yàn),結(jié)果如圖6所示。
圖6中,(a), (c), (e), (g)為Saling 實(shí)驗(yàn)數(shù)據(jù),(b), (d),(f), (h)為實(shí)驗(yàn)仿真。實(shí)線代表正常抓握(初始時(shí)拇指與食指基本閉合),虛線表示變異抓握(初始時(shí)手指最大限度張開)。抓握目標(biāo)分別為直徑2.2 cm(小物體)和6.7 cm(大物體)的物體。
5.3 目標(biāo)方向擾動(dòng)實(shí)驗(yàn)
圖7是方向變化時(shí)切向腕速度與抓握角度動(dòng)力學(xué)軌跡示意圖。圖7中,(a), (c), (e), (g)是Hoff-Arbib報(bào)告資料,(b), (d), (f), (h)是實(shí)驗(yàn)仿真。用作實(shí)驗(yàn)的物體被假定是一個(gè)直徑為1.5 cm的圓柱體。當(dāng)該物體被移動(dòng)偏離中線20°~ 30°時(shí),切向腕速度和抓握角度的運(yùn)動(dòng)學(xué)軌跡會(huì)有不同。第1行圖分別表示未受干擾的切向腕速度和抓握角度;第2行則分別表示受擾動(dòng)影響后的切向腕速度和抓握角度。
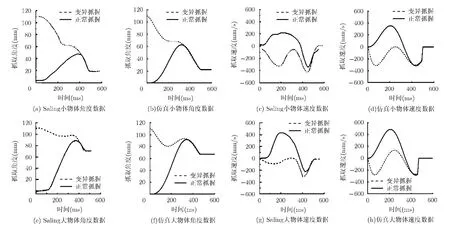
圖 6 正常抓握和變異抓握角度動(dòng)力學(xué)示意圖
從圖7中可以看到,目標(biāo)方向的變化使得手臂移動(dòng)和抓握角度兩者都受到影響,并且引起軌跡校正過程的暫時(shí)停止。擾動(dòng)時(shí)間越長,軌跡校正過程的暫停時(shí)間也越長。Hoff-Arbib 報(bào)告資料表明,在腕關(guān)節(jié)軌跡完成校正之前,大約會(huì)產(chǎn)生250~290 ms的延時(shí),并且整個(gè)運(yùn)動(dòng)時(shí)間平均要多出100 ms,這些圖中都有明確表示。為了適應(yīng)新的目標(biāo)位置,方向擾動(dòng)會(huì)引起運(yùn)動(dòng)校正過程的暫時(shí)停止這個(gè)結(jié)論也與Hoff-Arbib 報(bào)告完全一致。
5.4 目標(biāo)大小擾動(dòng)實(shí)驗(yàn)
圖8為目標(biāo)大小變化時(shí)抓握速度及角度動(dòng)力學(xué)軌跡示意圖。圖中,(a), (c), (e), (g)是Hoff -Arbib 報(bào)告資料,(b), (d), (f), (h)是實(shí)驗(yàn)仿真。圖中顯示了運(yùn)動(dòng)開始時(shí)目標(biāo)大小變化對抓握速度和角度的影響。用作實(shí)驗(yàn)的物體被假定是兩個(gè)直徑分別為 1.5 cm和 6 cm 的圓柱體。擾動(dòng)實(shí)驗(yàn)中,物體先是從小到大(S-L)變化,然后反過來從大到小(L-S)。第1行表示沒有擾動(dòng)時(shí)小物體的抓握運(yùn)動(dòng),第2行則表示有擾動(dòng)時(shí)物體從小到大變化的抓握運(yùn)動(dòng),第3行表示沒有擾動(dòng)時(shí)大物體的抓握運(yùn)動(dòng),第4行表示物體從大到小變化時(shí)的抓握運(yùn)動(dòng)。
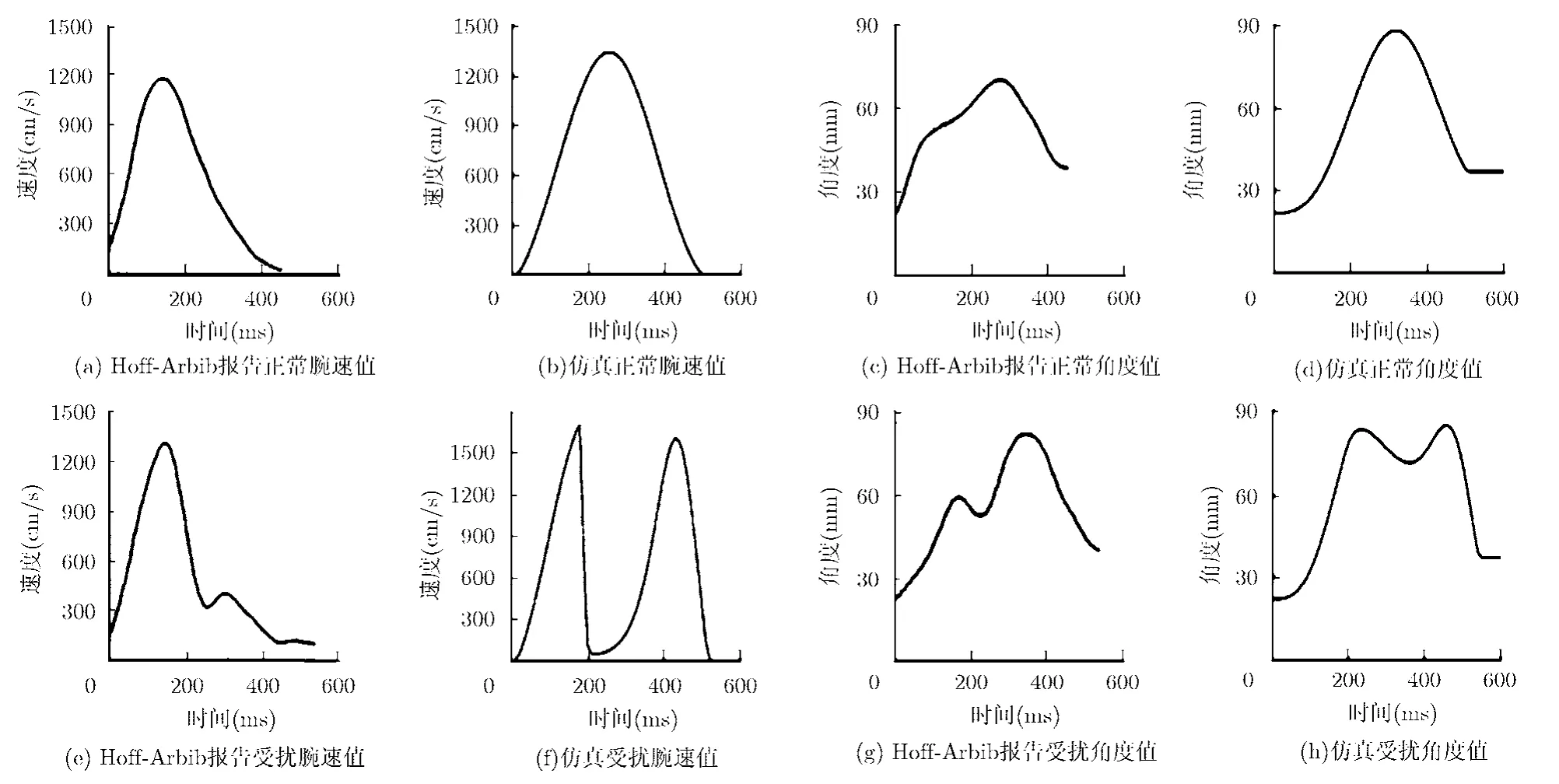
圖7 方向變化時(shí)切向位移和抓握角度動(dòng)力學(xué)軌跡示意圖
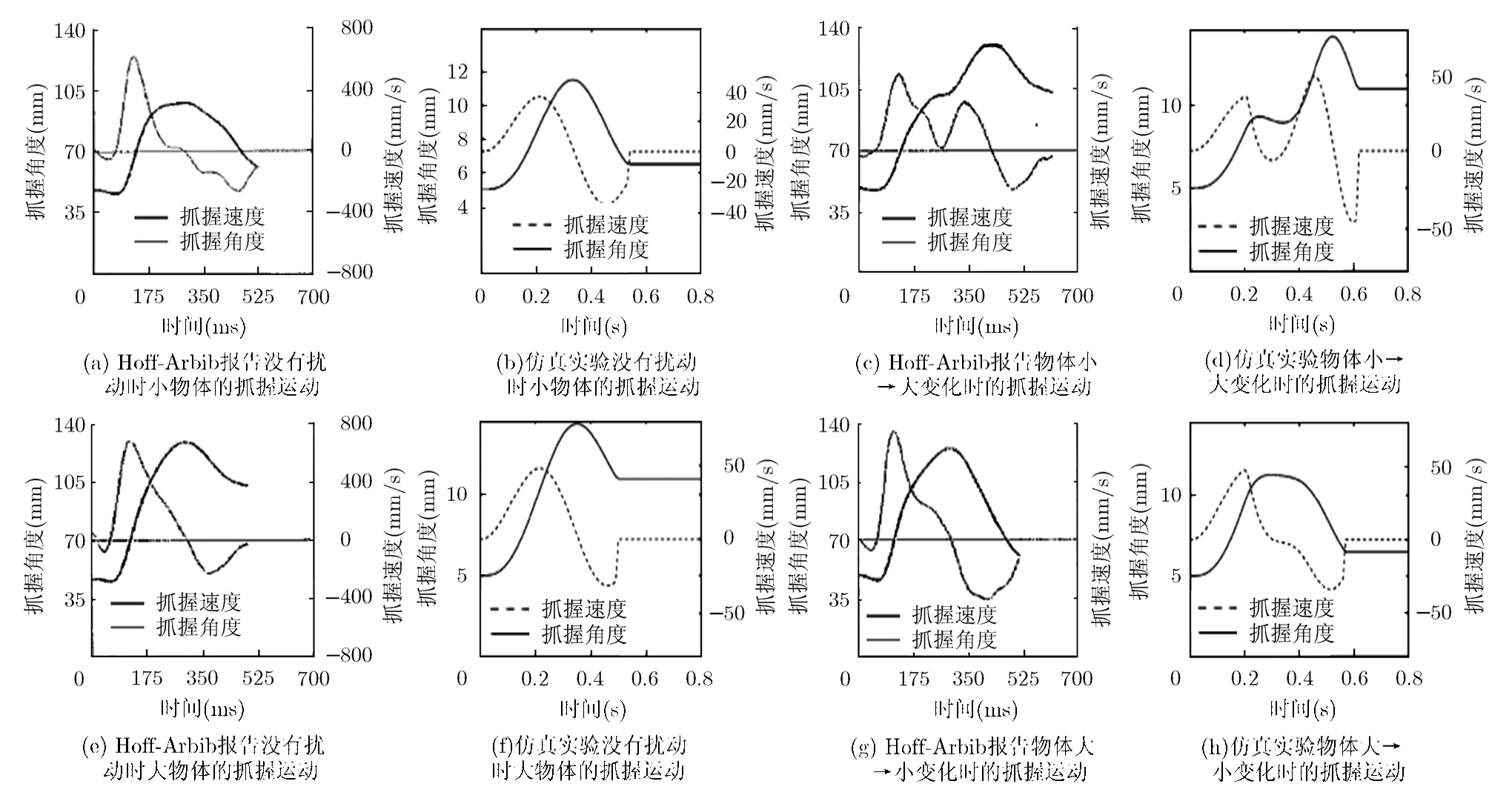
圖8 大小變化時(shí)抓握速度及角度動(dòng)力學(xué)軌跡示意圖
從圖8中可以看到,在小到大(S-L)擾動(dòng)實(shí)驗(yàn)中,抓握角度先是增加到與小目標(biāo)一致的峰值,然后又增加到與大目標(biāo)一致的最大角度,最后逼近大目標(biāo)。為了適應(yīng)新目標(biāo)變化尺寸,在抓握-延伸運(yùn)動(dòng)過程中,目標(biāo)大小的擾動(dòng)會(huì)引起校正過程的暫停,圖 8中清晰地表明了這一點(diǎn)。
6 結(jié)束語
針對手臂延伸與抓取的時(shí)間協(xié)調(diào)問題,本文提出一種具有小腦控制結(jié)構(gòu)且適用于2維空間的控制模型。該模型能夠?qū)崿F(xiàn)Hoff-Arbib模型所能實(shí)現(xiàn)的有關(guān)延伸與抓取運(yùn)動(dòng)動(dòng)力學(xué)的所有關(guān)鍵特征,有些性能甚至更好。在仿真方面,本文主要對模型進(jìn)行了 2維空間(方向和距離)的訓(xùn)練和學(xué)習(xí),相對于 1維空間訓(xùn)練,主要添加了抓取目標(biāo)所在方向的擾動(dòng)訓(xùn)練,明顯增強(qiáng)了模型控制系統(tǒng)的實(shí)用性和可拓展性。然而,對于該模型也有需要進(jìn)一步研究的問題。例如,在仿真訓(xùn)練過程中,本文分別介紹了目標(biāo)的大小變化以及目標(biāo)所在方向變化的抓握情況,下一步可關(guān)注更為綜合性的問題,即:如果在訓(xùn)練中同時(shí)改變目標(biāo)大小和方向位置會(huì)產(chǎn)生怎樣的效果;小腦控制模型能否適用于3維空間,等等。
[1] Webb B. Can robots make good models of biological behavior?[J]. Behavioral and Brain Sciences, 2001, 24(6):1033-1050.
[2] Zhang Shao-bai, Cheng Wei-qing, and Cheng Xie-feng. An application of cerebellar control model for prehension movements[J]. Neural Computing & Application, 2014, 24(5):1059-1066.
[3] Hoff B and Arbib M A. Models of trajectory formation and temporal interaction of reach and grasp[J]. Journal of Motor Behavior, 1993, 25(3): 175-192.
[4] Kawato M, Kuroda S, and Schweighofer N. Cerebellar internal models:implications for dexterous use of tools[J]. The Cerebellum, 2012, 11(2): 325-335.
[5] 張少白, 周寧寧. 用于機(jī)器人運(yùn)動(dòng)控制的通用小腦認(rèn)知模塊的構(gòu)建[J]. 南京郵電大學(xué)學(xué)報(bào)(自然科學(xué)版), 2012, 32(3):69-74.Zhang Shao-bai and Zhou Ning-ning . Development of general cerebellar cognitive module used for robot motor control[J].Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2012, 32(3): 69-74.
[6] Jaeger D. Cerebellar Nuclei and Cerebellar Learning[M]. New York: USA, Handbook of the Cerebellum and Cerebellar Disorders, 2013, 4: 1111-1130.
[7] Townsend B R and Subasi E. Grasp movement decoding from premotor and parietal cortex[J]. The Journal of Neuroscience,2011, 31(40): 14386-14398.
[8] Bruno B and Peter E. Neural correlations, population coding and computation[J]. Nature Reviews Neuroscience , 2006, 7:358-366.
[9] 張少白, 阮曉鋼. 仿生機(jī)械臂的小腦控制模型和仿真[J]. 電子學(xué)報(bào), 2007, 35(5): 991-995.Zhang Shao-bai and Ruan Xiao-gang. A cerebellar control model and simulation of biomimetic manipulator[J]. Acta Electronica Sinica, 2007, 35(5): 991-995.
[10] Kawato M, Masa-aki Sato, Taku Yoshioka. Hierarchical Bayesian estimation for MEG inverse problem[J].NeuroImage, 2004, 23(3): 806-826.
[11] Saling M, Mescheriakov S, Molokanova E, et al.. Grip reorganization during wrist transport: the influence of analtered aperture[J]. Experimental Brain Research, 1996,108(3): 493-500.

