一種改進的極化敏感陣列解相干算法

李會勇 劉 芳謝菊蘭 樊 勇

(電子科技大學電子工程學院 成都 611731)

1 引言

極化敏感陣列能夠獲取入射信號完備的電場分量和磁場分量，因而具有比傳統標量陣列更優越的系統性能[13]-。極化敏感陣列信號處理大多假定信號源之間是互不相干的，但是在實際環境中空間多徑傳播、敵方轉發干擾等因素都將導致信號源之間存在相干性。當信號源之間相干時，信號自相關矩陣的秩不再是滿秩矩陣，這時基于子空間的參數估計和波束形成算法都將有嚴重的性能下降甚至失效[4,5]，因此必須在自適應陣列處理算法之前，對接收信號進行解相干處理。

常用的極化敏感陣列解相干算法大致有兩類[6]：一是空間平滑算法，它以降低陣列的有效孔徑為代價恢復信號相關矩陣的秩，但它需要一個規則的陣列結構，當信號到達角相近時，其解相干性能下降甚至失效[7,8]；另一類是極化平滑算法，它是利用陣列各陣元不同類型的極化分量進行均勻平滑，沒有降低陣列的有效孔徑，對陣列的空間幾何結構也沒有限制，即使信號到達角度相近時也能很好地完成解相干[9]。因此，極化平滑算法具有比空間平滑算法更多的優勢，但是極化平滑算法并不能對任意相干信號實現完全解相干，陣列的解相干性能還有待進一步提高。文獻[10,11]中對極化平滑算法進行了改進，通過對子陣的自相關矩陣進行非均勻加權處理，在空間非均勻噪聲環境下具有比極化平滑更好的性能，但是解相干之后信源之間仍然具有相關性。文獻[12]中提出了另一種加權極化平滑算法，它對接收陣列協方差矩陣的36個子矩陣做加權滑動平均，并對平滑之后的等效信號協方差矩陣施加對角化約束其計算量較大，并且文獻[12]的方法需要預先進行去噪處理和獲得大致的入射信號參數包括波達角度和極化參數，這無疑大大增加了算法處理的復雜度，不利于工程實現。文獻[13]利用線性電磁矢量陣列采用傳播算子的方法，完成了相干信號的多參數聯合估計，該文把極化平滑和空間平滑同時用于解相干，這在一定程度上降低了陣列的自由度。本文在極化平滑算法的基礎上，通過對各子相關矩陣選擇非均勻的加權系數，使平滑之后的相關矩陣具有Toeplitz的形式，進而最大可能地消除了信號之間的相干性，具有實現簡單、計算量少且不會降低陣列自由度的優勢。通過計算機仿真把非均勻平滑之后的相關矩陣應用到參數估計和波束形成算法[14,15]中，完成了相干信號的波達方向估計和自適應波束形成，仿真結果表明本文方法具有比常規極化平滑方法更優越的性能。

2 信號模型

完備的電磁矢量傳感器由相互正交的3個電偶極子和3個磁偶極子構成，它們在空間同點放置，能同時接收空間中完備的電場分量和磁場分量。對于完全極化波，陣元接收信號的極化導向矢量[3]表示為

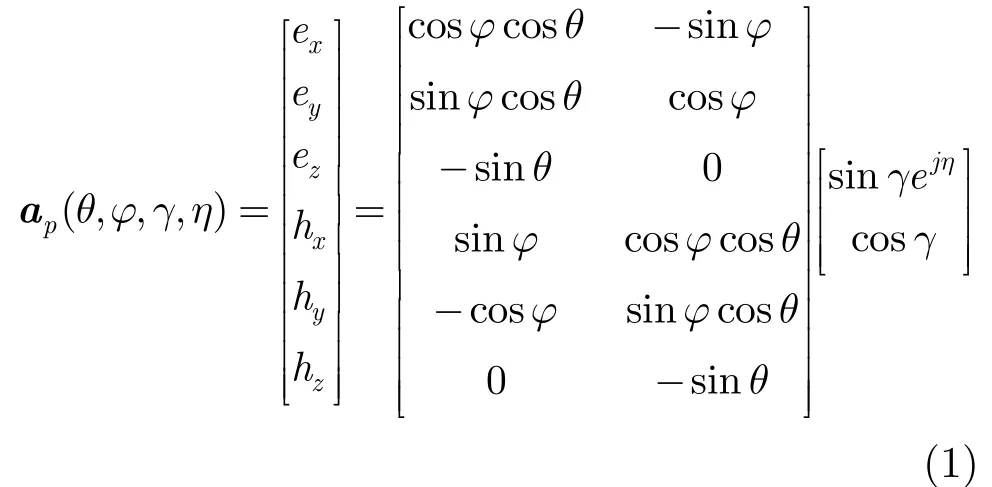
假設有M個陣元構成極化敏感陣列，每個陣元由L個電磁分量構成，對于空間入射的K個相干窄帶信號，接收信號模型可以表示為

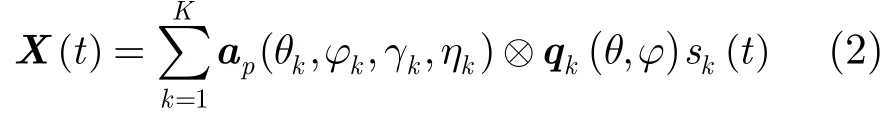
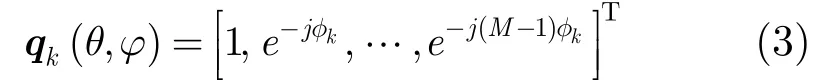
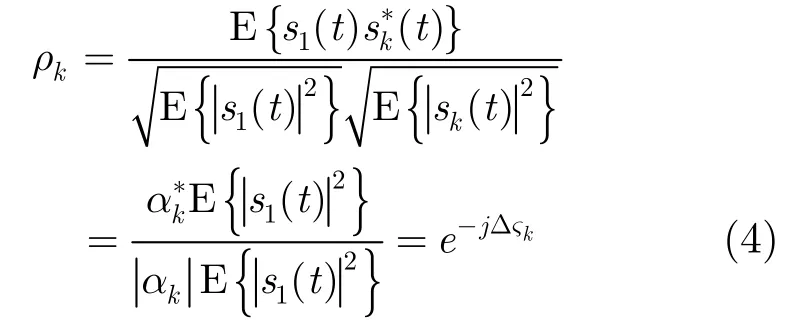
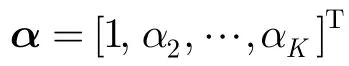
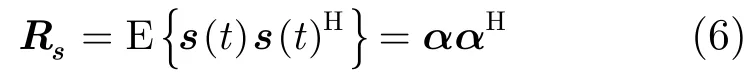
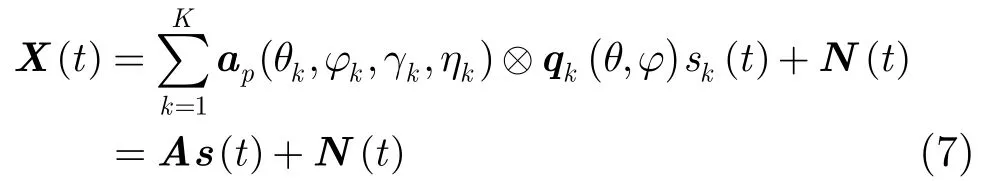
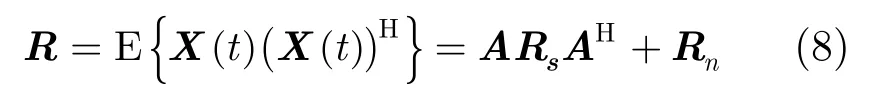
可見，自相關矩陣R的秩受限于sR 的秩，所以在自適應陣列處理算法之前，必須得先對接收信號進行解相干處理。下面將介紹極化平滑解相干算法。

3 解相干算法描述

3.1 極化平滑

各陣元由L個分量構成，現在僅考慮陣列相同類型的極化分量第l分量[4]的輸出：

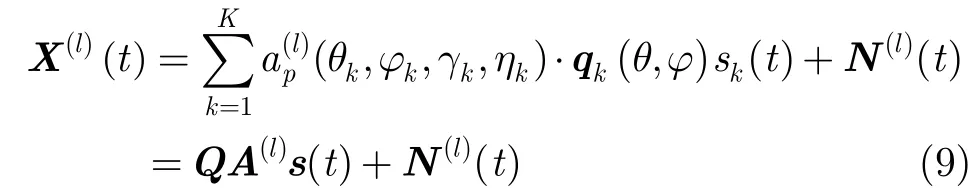
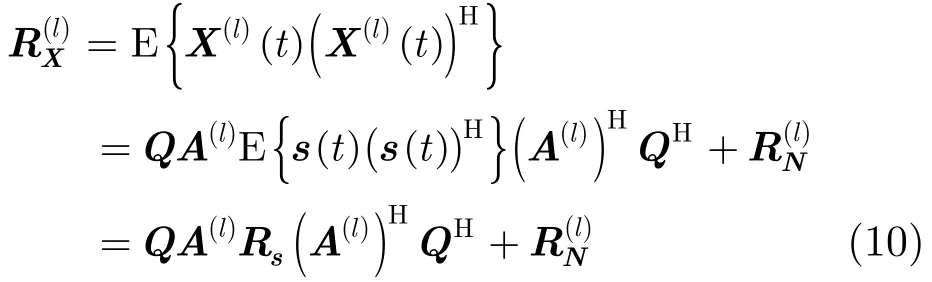
常規的極化平滑算法就是把各子陣的相關矩陣進行均勻加權求和，以降低信號之間的相關性[4]。均勻極化平滑之后的相關矩陣為

其中

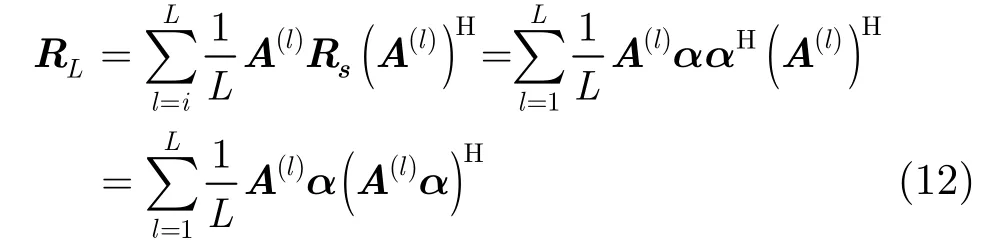
3.2 非均勻加權極化平滑

若入射信號為互不相干的平穩隨機過程，則陣列接收信號的相關矩陣R為Toeplitz矩陣，即對角線上的元素相等[5]。當信號相干時會導致平滑之后的相關矩陣偏離 Toeplitz的形式，因此可以選擇適當的加權系數，使加權平滑之后的相關矩陣仍為Toeplitz矩陣，這樣就實現了對相干信號的解相干，有

為了衡量加權平滑之后的相關矩陣偏離Toeplitz矩陣的程度，將XR 中各元素與其所在對角線上元素均值的方差和作為代價函數：

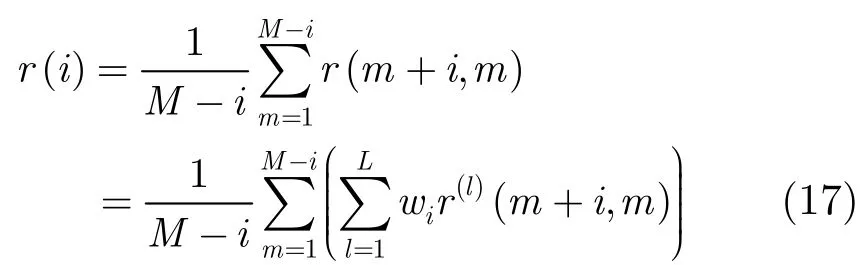
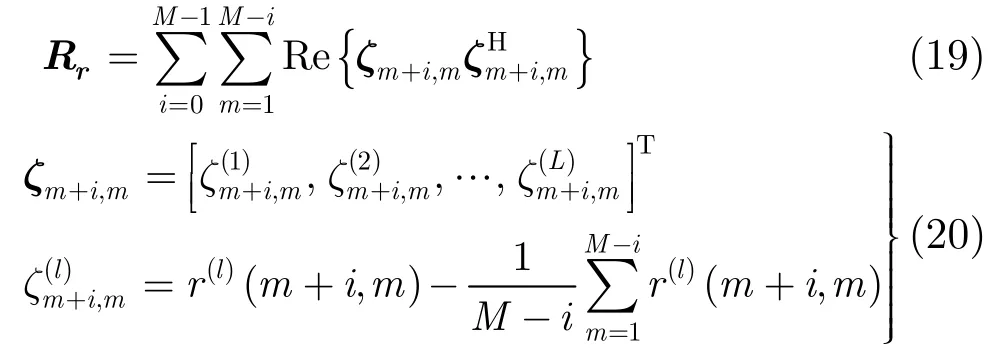
將最優加權系數代入到式(15)中，就可求得非均勻加權極化平滑之后的最接近Toeplitz形式的信號相關矩陣，完成了對相干信號最大程度的解相干。

由M個陣元構成的極化敏感陣列共含有ML個傳感器單元，從上面的分析可得極化平滑算法是對L個維的相關矩陣進行滑動平均，一般我們用N次采樣快拍得到的接收數據來估計，即

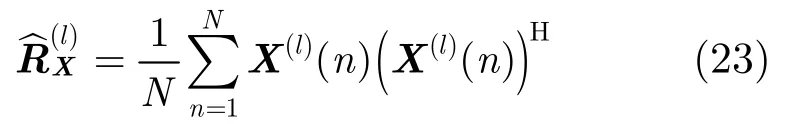
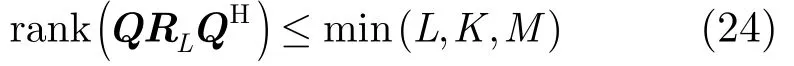
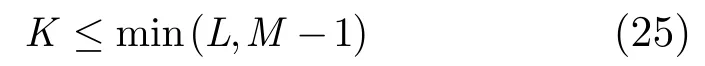
即當入射相干信號個數滿足上述要求時可以用本文方法實現解相干。

4 仿真分析

仿真條件1 5陣元均勻線陣，每個陣元由6個分量構成，陣元間距，入射信號為一個期望信號和與之相干的干擾信號。實驗中入射信號均為遠場窄帶信號，仿真中只考慮其包絡，考慮期望信號的復包絡，其中1A為期望信號的幅度，由信噪比決定，表示噪聲功率，歸一化頻率是在上服從均勻分布的隨機相位，相干干擾信號，其中，表示干擾信號相對期望信號的幅度衰落和相位差。期望信號到達角，極化相角，極化相位差。干擾信號參量。噪聲為均值為 0，方差的高斯白噪聲。圖1給出了不同的平滑算法對 MVDR波束形成方向圖的影響(圖中PS和WS分別代表常規的極化平滑算法和本文算法)。從仿真結果可以看出兩種方法都將波束主瓣對準了期望信號方向，同時本文方法比常規極化平滑方法在干擾方向形成了更深更精確的零陷，而普通的MVDR算法在干擾來波方向并沒有零陷。

仿真條件2 4陣元均勻線陣，每個陣元由6個分量構成，入射信號為4個相干的窄帶信號，期望信號與仿真條件1相同，干擾信號。信噪比、干噪比及噪聲設置同仿真條件1。期望信號到達角，極化參數。3個干擾信號的俯仰角分別為，方位角都為，干擾信號的極化參量分別為,。圖2給出了不同的平滑算法對 MVDR波束形成方向圖的影響。從仿真結果可以看出，本文算法當入射信號個數與陣元數相同時，即時也能很好地完成解相干。

仿真條件3 入射信號參量同仿真條件1，當輸入信號信噪比變化時圖 3給出了均勻平滑(PSMUSIC)算法和文獻[11]中的 modified PAS in element-space算法和本文算法對Root-Music參數估計均方根誤差的影響，并對比分析了相干信號和部分相關(仿真中設置情況下的性能對比。從仿真結果可以看出3種算法在平滑處理之后都能很好地完成信號的解相干，且本文算法具有更低的均方根誤差，且在入射信號部分相關的情況下也具有較好的解相干性能。

仿真條件4 基本仿真條件同仿真條件1。由于極化敏感陣列各陣元在空間共點放置，使得各共點通道之間接收噪聲存在一定的相干性，考慮各通道接收噪聲為相干的高斯白噪聲，且噪聲與入射信號不相關。圖4給出了通道相干噪聲對不同算法解相干性能的影響。從仿真結果可以看出，在相干噪聲的情況下本文算法和文獻[11]中的算法都具有較好的解相干性能，且本文算法具有更低的均方根誤差，與圖 3對比可以看出常規的極化平滑算法性能下降。

仿真條件5 基本仿真條件同仿真條件1。考慮非均勻噪聲對本文算法的影響，噪聲與入射信號不相關。圖5給出了通道非均勻噪聲對不同算法解相干性能的影響，非均勻噪聲的協方差矩陣設置同文獻[16]中的式(2)，且主對角元素是在區間(0,5]上均勻分布的隨機變量。從仿真結果可以看出，在非均勻噪聲的情況下本文算法和文獻[11]中的算法都具有較好的解相干性能，且文獻[11]中的算法具有更低的均方根誤差，但從算法的推導可知文獻[11]中的算法同時利用了子陣的自相關和互相關信息，具有更大的算法計算量。與圖3對比可以看出常規的極化平滑算法在非均勻噪聲情況下性能下降。

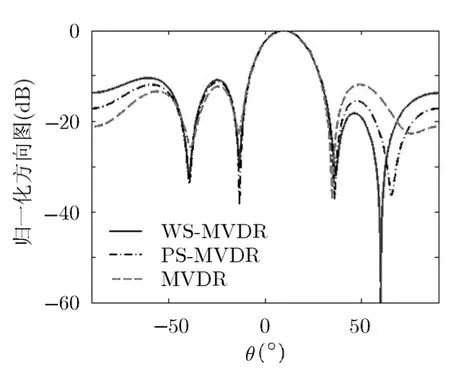
圖1 不同平滑算法對陣列方向圖的影響

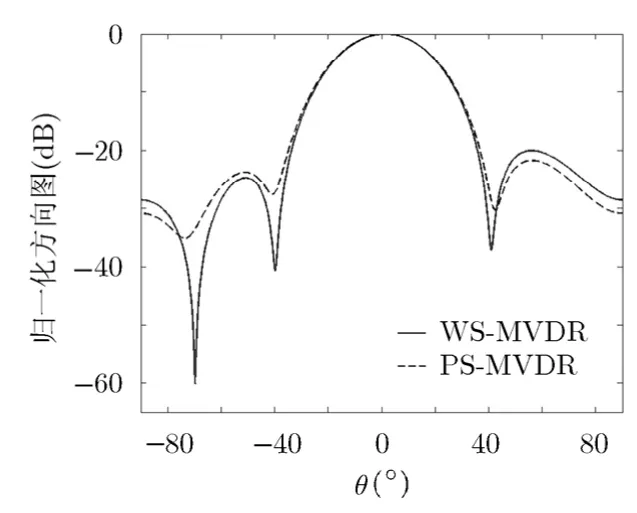
圖2 多個相干信號對波束圖的影響

圖3 不同平滑算法參數估計均方根誤差對比

圖4 相干噪聲對算法性能的影響

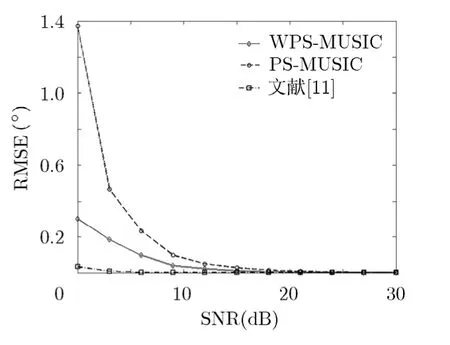
圖5 非均勻噪聲對算法性能的影響

5 結束語

本文在常規極化平滑算法的基礎上，通過對各子陣相關矩陣進行非均勻加權實現了對任意相干信號的解相干。計算機仿真結果表明本文方法無論是應用于參數估計還是波束形成都比常規極化平滑算法具有更優的性能，且在相干噪聲或非均勻噪聲的背景下也具有很好的算法適應性。

[1] Nehorai A and Paldi E. Vector-sensor array processing for electromagnetic source localization[J]. IEEE Transactions on Signal Processing, 1994, 42(2): 376-398.

[2] Wong K T and Yuan X. “Vector cross-product directionfinding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles or loops[J]. IEEE Transactions on Signal Processing, 2011, 59(1):160-171.

[3] 莊釗文, 徐振海, 肖順平, 等. 極化敏感陣列信號處理[M]. 北京: 國防工業出版社, 2005: 16-34.

[4] Nikolic M M, Nehorai Arye, and Djordjevic A R. Estimation of direction of arrival using multipath on array platforms[J].IEEE Transactions on Antennas and Propagation, 2012,60(7): 3444-3454.

[5] 何子述, 夏威, 等. 現代數字信號處理及其應用[M]. 北京: 清華大學出版社, 2010: 301-320.

[6] 林智勇, 陶建武. 基于矢量平滑的相關源MVDR波束成形[J].通信學報, 2013, 34(1): 96-103.Lin Zhi-yong and Tao Jian-wu. MVDR beamforming for correlated signal with vector smoothing[J]. Journal on Communications, 2013, 34(1): 96-103.

[7] Thakre A and Haardt M, and Giridhar K. Single snapshot spatial smoothing with improved effective array aperture[J].IEEE Signal Processing Letters, 2009, 16(6): 505-508.

[8] 王偉偉, 梁廣真. 基于均分陣元的空域平滑技術研究[J]. 現代電子技術, 2013, 36(9): 82-83.Wang Wei-wei and Liang Guang-zhen. Research of spatial smoothing technique based on split array element[J]. Modern Electronics Technique, 2013, 36(9): 82-83.

[9] Rahamim D, Tabrikian J, and Shavit R. Source localization using vector sensor array in a multipath environment[J].IEEE Transactions on Signal Processing, 2004, 52(11):3096-3013.

[10] He Jin, Jiang Sheng-li, Wang Ju-ting, et al.. Polarization difference smoothing for direction finding of coherent signals[J]. IEEE Transactions on Aerospace and Electronic Systems,2010, 46(1): 469-480.

[11] Xu Y and Liu Z. Polarimetric angular smoothing algorithm for an electromagnetic vector-sensor array[J]. IET Radar,Sonar ＆amp; Navigation, 2007, 1(3): 230-240.

[12] 鄭桂妹, 陳伯孝, 楊明磊, 等. 基于電磁矢量陣列的加權極化平滑解相干算法[J]. 系統工程與電子技術, 2012, 34(4):637-643.Zheng Gui-mei, Chen Bai-xiao, Yang Ming-lei, et al..Weighted polarization smoothing algorithm for electromagnetic vector-sensor array[J]. Systems Engineering and Electronics, 2012, 34(4): 637-643.

[13] 劉兆霆, 何勁, 劉中. 線性電磁矢量陣列的空時極化平滑算法及相干源多參數估計[J]. 電子與信息學報, 2010, 32(12):3032-3036.Liu Zhao-ting, He Jin, and Liu Zhong. Spatial-temporal polarization smoothing for joint frequency, 2-D DOA, and polarization estimation of coherent sources with linear electromagnetic vector sensor array[J]. Journal of Electronics＆amp; Information Technology, 2010, 32(12): 3032-3036.

[14] Wong K T, Li Lin-shan, and Zoltowski M D. Root-Musicbased direction-finding and polarization estimation using diversely-polarized possibly-collocated antennas[J]. IEEE Antennas and Wireless Propagation Letters, 2004, 3(1):129-132.

[15] 田靜, 廖桂生, 楊志偉. 極化敏感陣列斜投影濾波性能分析[J].雷達學報, 2013, 2(3): 284-291.Tian Jing, Liao Gui-sheng, and Yang Zhi-wei. Performance analysis of oblique projection filtering based on polarization sensitive array[J]. Journal of Radars, 2013, 2(3): 284-291.

[16] 劉國紅, 孫曉穎, 王波. 非均勻噪聲下頻率及二維到達角的聯合估計[J]. 電子學報, 2011, 39(10): 2427-2430.Liu Guo-hong, Sun Xiao-ying, and Wang bo. Joint estimation for frequency and 2-D DOA in nonuniform noise[J]. Acta Electronica Sinica, 2011, 39(10): 2427-2430.