一種新的基于不變矩的步態特征身份識別算法

汪西原，閆 輝

(寧夏大學物理電氣信息學院，寧夏銀川750021)

1 算法簡介

由于人體步態特征具有難以偽裝，正常情況下不易修改，識別時具有遠距離非接觸，對系統分辨率要求低的特點而逐漸成為模式識別研究領域的一個重點。步態識別算法可分為基于模型(橢圓模型［1］、鐘擺模型［2］、三維模型［3］等)和基于特征兩種。由于運動過程中步態特征的復雜性，基于模型的方法描述步態運動具有一定的局限性。基于特征的方法如陳實等人［4］采用極直方圖的方法描述步態輪廓;Rahati等人［5］采用小波變換;馬勤勇等人［6］利用一幅步態輪廓圖提取三段步態輪廓線;楊旗等人［7］提出的動靜態信息融合及動態貝葉斯網絡的步態識別算法等。但是，當人體目標與攝像機在相對運動過程中出現幾何變化(位置、尺度和方向)時，上述基于特征的方法無法獲得準確的步態特征信息，因此識別的正確率會降低，而利用不變矩提取的特征對發生幾何變化的圖像也有很好的不變性，尤其可以很好地描述視頻序列中單幀人體形狀的步態特征，如林敏等人［8］提出了一種基于統一Hu矩和支持向量機的步態識別算法;張前進等人［9］提出了基于Radon變換特征提取的步態識別;Xiao等人［10］提出了基于Zernike矩和BP神經網絡的步態識別算法;Lu［11］利用偽Zernike矩聯合付立葉描述子和小波描述子并采用決策級融合的方法進行步態特征識別。但是，這些基于不變矩的步態識別算法需要對視頻序列中檢測到的灰度目標圖像進行二值化和歸一化處理，之后再進行不變性特征的提取，而二值化過程會造成很多細節與有用信息丟失，歸一化過程則會引入重采樣與重量化誤差，這必然導致算法識別率的降低。

為了克服上述不足，本文將基于Radon變換和解析Fourier－Mellin變換［12］的不變性特征提取算法應用于步態識別。由于直接對灰度圖像進行特征提取，沒有二值化和歸一化，因此得到的特征具有更多的細節信息，對原圖像有更好的描述能力。圖1和圖2為兩種算法實現框圖。

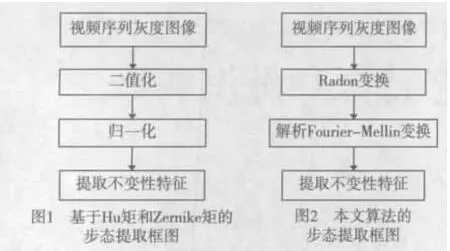
2 相關工作

該算法首先對目標灰度圖像利用Radon變換(見圖2)將原圖像的旋轉變化轉化到沿H方向平移的投影空間(見圖3)，尺度變化轉換為在r軸的尺度與幅度變化，然后對Radon投影空間利用解析Fourier－Mellin變換進一步變換，由此即可實現將Radon投影空間H方向的平移和r軸的尺度變化與幅度變化分別轉化為相位因子和幅度變化，最后即可通過定義一些具有旋轉與尺度不變性的函數提取步態特征，應用分類算法實現分類識別。

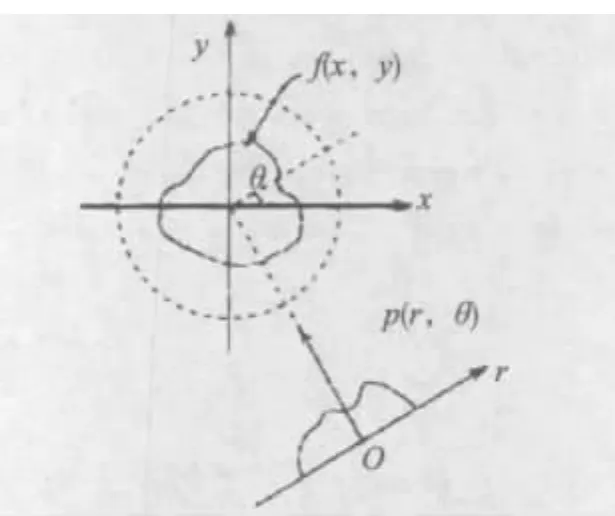
圖3 f(x，y)的Radon變換

2.1 Radon變換及其性質

對于一個二維函數f(x，y)，它的Radon變換就是該函數沿平面內不同的直線的線積分，如圖3所示。其定義如下

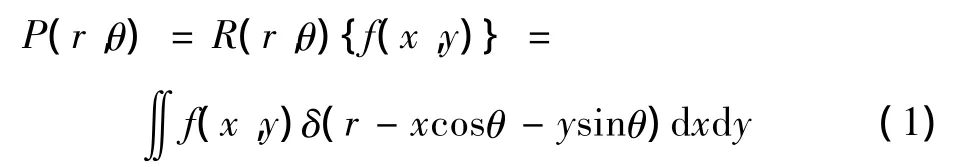
對于圖像的幾何變換，Radon變換有以下性質:

1)平移性質

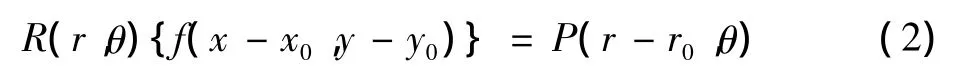
2)旋轉性質

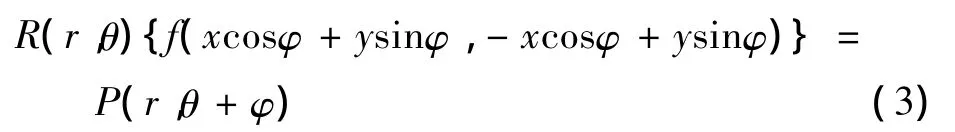
3)尺度變換性質

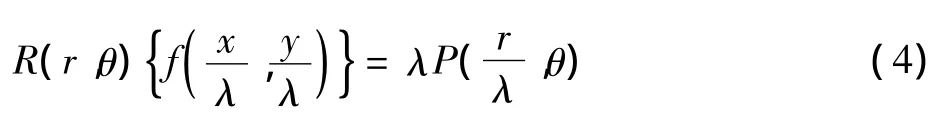
2.2 解析 Fourier－Mellin 變換

用極坐標表示的情況下，二維函數g(r，θ)的解析Fourier－Mellin變換的定義式為

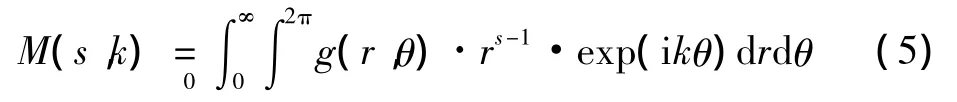
式中:s=σ－iu，u為實數變量，σ為大于0的實常數，一般取值為0.5。因此式(5)可以寫為

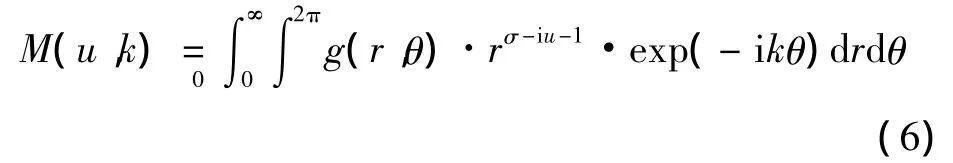
3 本文算法描述

本文對于步態的識別過程主要分為兩個步驟，首先是對視頻序列中檢測到的人體運動目標進行步態周期的檢測并得到一個步態周期的關鍵幀，其次是利用不變性特征函數對得到的關鍵幀提取不變性特征并用K近鄰分類算法對特征進行分類識別。

3.1 步態周期檢測

根據人體寬度變化分析步態周期是一種相對簡單的方法，人體下肢的寬度變化一般不會受到其他因素的影響，因此本文根據人體下肢區域寬度來分析步態周期。此處的下肢區域的高度指的是膝蓋到腳底的距離，這個距離既不會受到上肢的影響，也可以很好地反映步態周期的變化。需要說明的是，根據醫學對人體研究表明，膝蓋到腳底的高度約為人體高度的0.260倍，如圖4所示［13］。

在正常的行走狀態下，步態具有重復性，也就是說具有準周期性。根據醫學上對步態周期的定義，如圖5所示，以右腳跟著地為起始點，當左腳跟著地時為半個周期，當右腳跟再次著地時即為一個步態循環。因此，根據人體下肢的寬度變化就可以得到人體運動的周期。

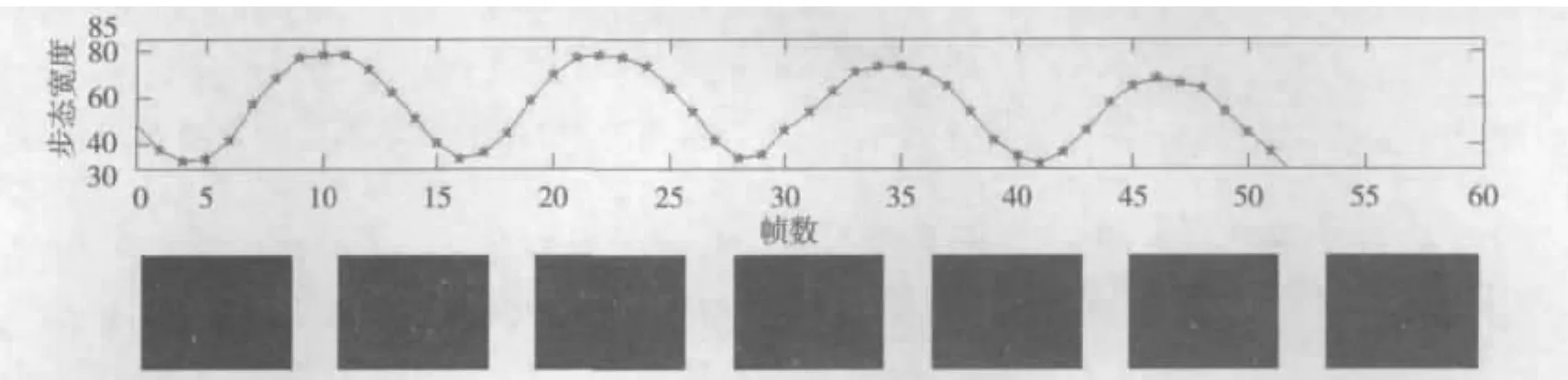
圖5 人體步態周期分析

由于已采用上述方法檢測到了一個運動周期內步態寬度的最大值和最小值，可以將這些極值幀作為關鍵幀，如果想得到更多的關鍵幀，可以在極值幀之間選取得到。

3.2 步態特征提取及識別

設圖像f(x，y)經過尺度因子λ與角度旋轉φ變換后獲得的圖像為(x，y)表示，則由式(2)～式(4)可得(x，y)的Radon變換為

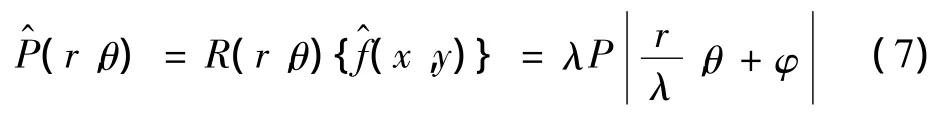
式中:P(r，θ)是函數f(x，y)的 Radon 變換。對P^(r，θ)進行Fourier－Mellin變換后有

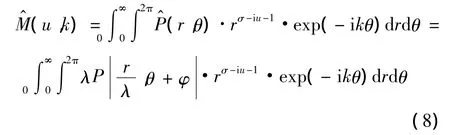
dr=λdτ ，dθ=dβ ，式(8)可變為

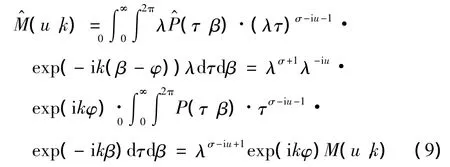
式中:M(u，k)為函數P(r，θ)的 Fourier－Mellin 變換。

由式(9)可以看出原圖像f(x，y)的旋轉和尺度變換經過Radon變換和Fourier－Mellin變換后轉化為相位和幅度因子，由此可以定義函數

由式(9)和式(10)可得

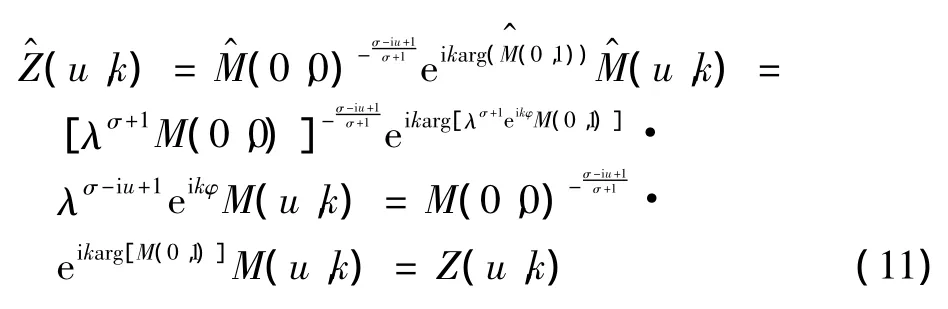
由式(11)可知，函數Z(u，k)與原圖像的旋轉和尺度變換無關，因此基于不變函數Z(u，k)提取旋轉和尺度變換后圖像的不變性特征如下

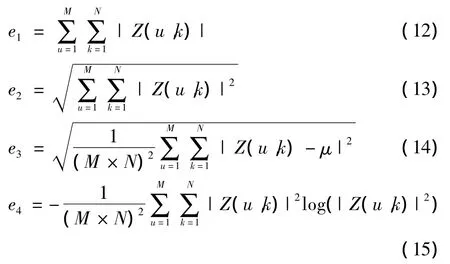
4 仿真實驗結果

算法采用MATLAB2008編程進行實驗仿真。所采用的數據庫(CASIA步態數據庫)是由中科院自動化所提供，本實驗從中分別選取了10個人和20個人，每個人有2個步態的視頻序列。每個人的一個步態視頻作為訓練樣本，另一個作為測試樣本，分別采用Hu矩、Zernike矩和本文的不變矩進行步態特征的提取和識別。此處本實驗選取了1個步態周期內的8幅關鍵幀圖像(如圖6所示)進行步態特征的提取，其圖像和對應的不變矩特征如表1～表3所示。

圖6 1個步態周期的關鍵幀圖像

表中F1，F2，…，F8表示圖6中從左至右每一個關鍵幀圖像，e，H，Z分別代表不同算法得到的矩特征。

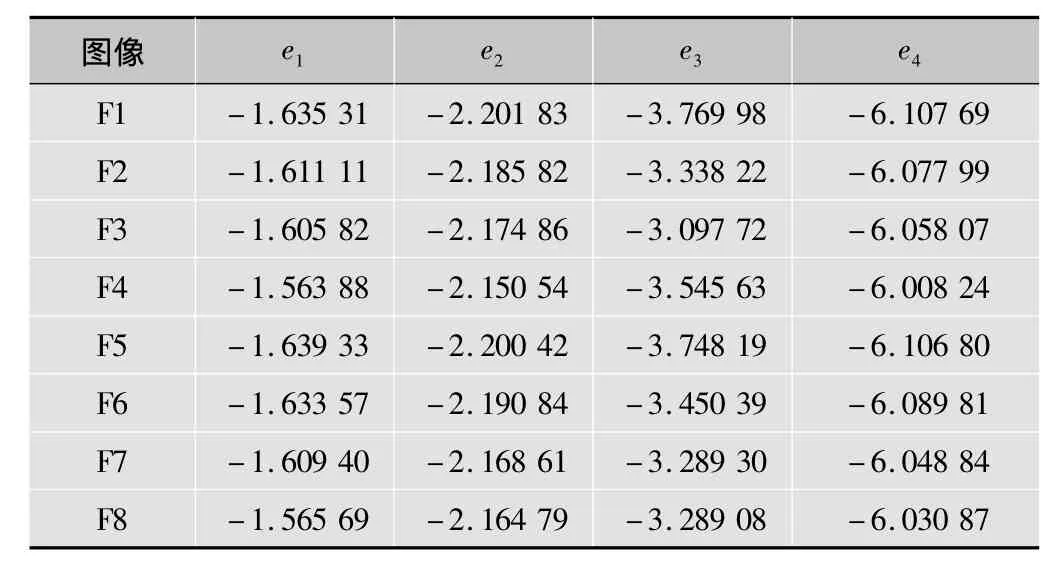
表1 本文不變矩提取不變性特征得到的特征值

采用K近鄰算法分類得到的識別正確率如表4所示。由表4可以看出，在均采用K近鄰分類算法時，本文提出的步態特征提取算法的分類能力較好，有效解決了目前基于不變矩的步態特征提取算法需要對灰度圖像進行二值化和歸一化的問題，克服了目前方法僅能對二值圖像提取步態特征的不足，同時，采用本文算法提取的步態特征的分類正確率遠高于目前采用Hu矩和Zernike矩的方法，說明本文算法應用于步態識別是可行且更有效的。

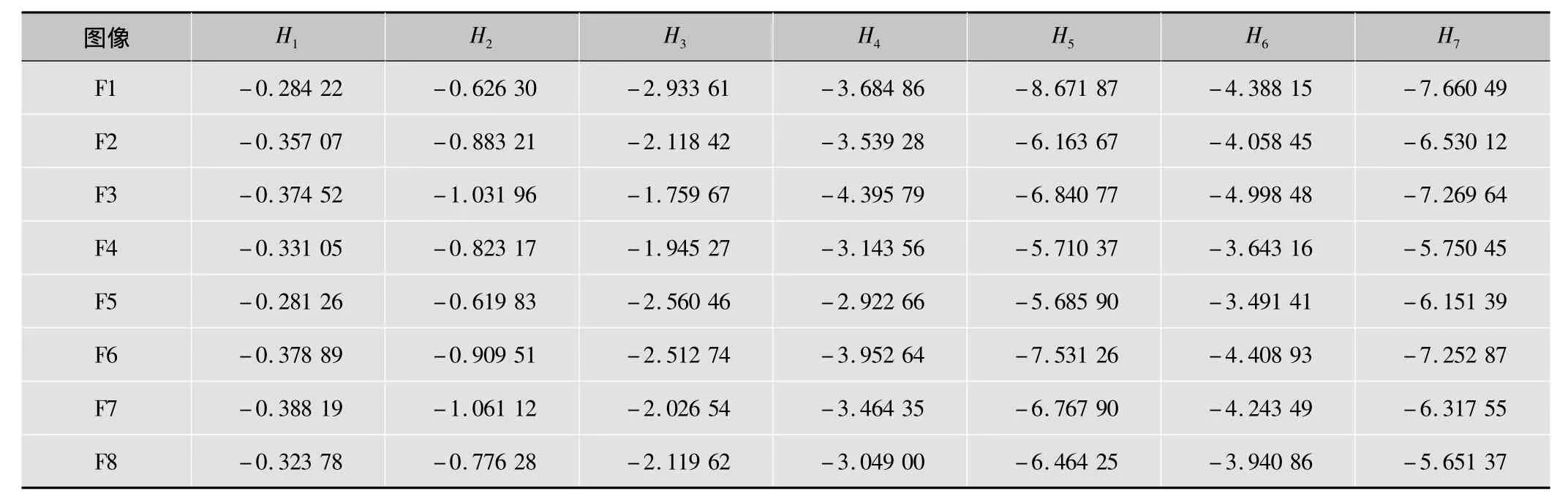
表2 Hu不變矩不變性特征得到的特征值

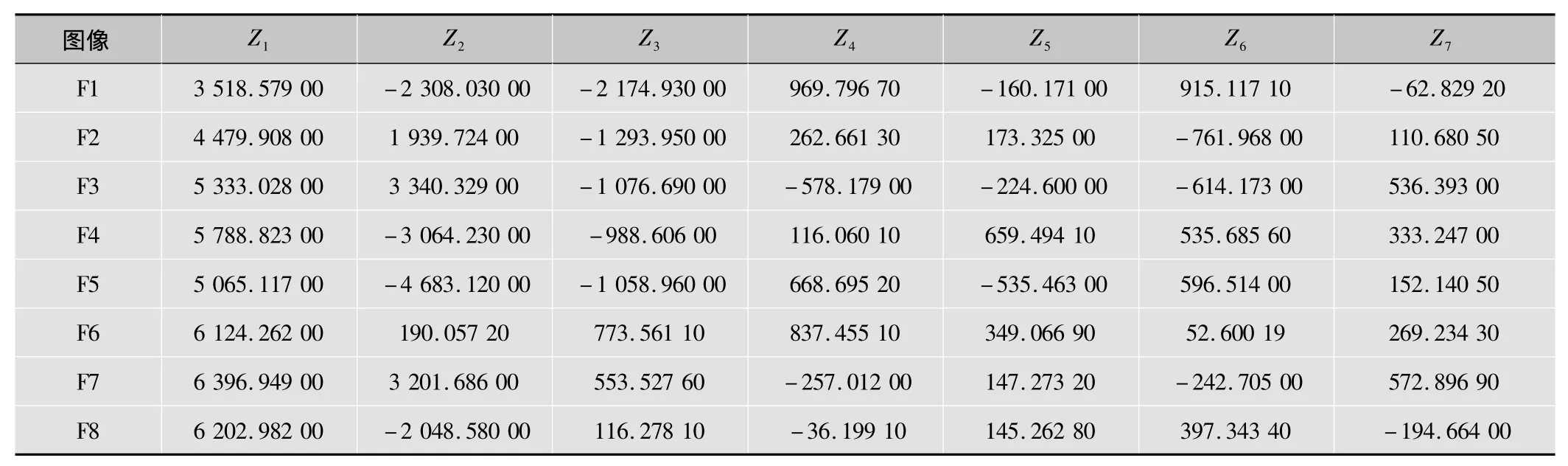
表3 Zernike不變矩不變性特征得到的特征值

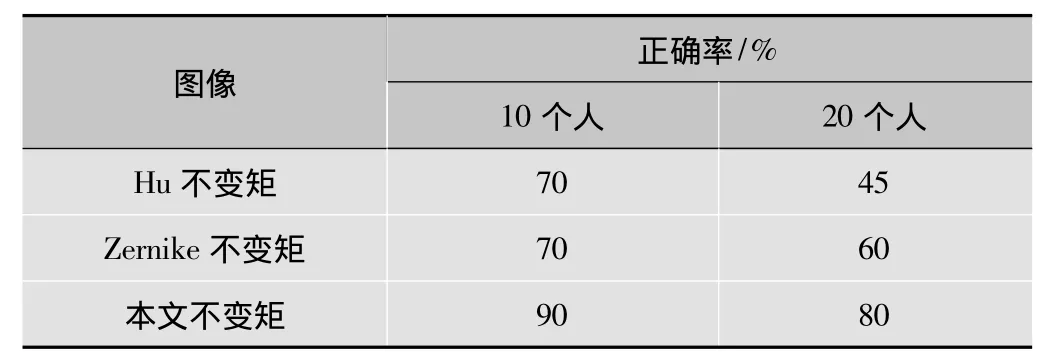
表4 3種算法的分類正確率

5 結論

本文提出了一種基于Radon變換和解析Fourier－Mellin變換的步態識別算法，該算法首先對灰度圖像進行Radon變換，之后再進一步進行Fourier－Mellin變換，這樣就避免了目前基于不變矩的方法對灰度圖像二值化和歸一化時所造成的量化誤差和細節信息的丟失，因此，采用本文算法提取的特征更準確地描述了步態信息，進行步態識別有更高的識別率。但是，與目前成熟的指紋、虹膜等識別方法相比，本文算法的識別率還有待于進一步提高，尤其是當樣本數據增大時，識別率也明顯下降，下一步工作的研究重點是將本文算法提取的特征與顏色、紋理、人耳或人臉等一種或多種特征融合以提高算法識別率，同時考慮采用快速Fourier變換來提高算法執行效率，使本文算法最終達到實際應用的目的。

［1］ XU JH，WANGC，LIJ，etal.Gait recognition based on key frame and ellipticalmodel［C］//Proc.2010 IEEE International Conference on Information and Automation(ICIA).Harbin，China:IEEE Press，2010:2483－2487.

［2］ HEW H，LIP.Gait recognition using the temporal information of leg angles［C］//Proc.2010 3rd IEEE International Conference on Computer Science and Information Technology.Chengdu，China:IEEE Press，2010:78－83.

［3］ JEGOON R，KAMATA S.Front view gait recognition using spherical spacemodelwith human point clouds［C］//Proc.2011 18th IEEE International Conference on Image Processing.Brussels，Belgium:IEEE Press，2011:3209－3212.

［4］ CHEN S，GAO Y X.An invariant appearance model for gait recognition［C］//Proc.2007 IEEE International Conference on Multimedia and Expo.Beijing，China:IEEE Press，2007:1375－1378.

［5］ RAHATI S，MORAVEJIAN R，KAXEMI F M.Gait recognition using wavelet transform［C］//Proc.the Fifth InternationalConferenceon Information Technology:New Generations.Las Vegas，USA:［s.n.］，2008:932－936.

［6］馬勤勇，聶棟棟，王申康.基于主運動輪廓線的步態表示與識別［J］.自動化學報，2009，35(5):519－525.

［7］楊旗，薛定宇.動靜態信息融合及動態貝葉斯網絡的步態識別［J］.中國圖象圖形學報，2012，17(7):783－790.

［8］林敏，吳清江.基于統一Hu和支持向量機的步態識別［J］.微計算機信息，2010，26(13):197－199.

［9］張前進，徐素莉，孫炎增.基于Radon變換特征提取的步態識別［J］.數據采集與處理，2010，25(2):268－272.

［10］ LU JW，ZHANG E H.Gait recognition for human identification based on ICA and fuzzy SVM throughmultiple views fusion［J］.Pattern Recognition Letters，2007，28(16):2401－2411.

［11］ XIAO D G，YANG L.Gait recognition using zernike moments and BP neural network［C］//Proc.2008 IEEE International Conference on Networking，Sensing and Control.Sanya， China:IEEE Press，2008:418－423.

［12］ WANG X，XIAOB，MA JF，etal.Scaling and rotation invariantanalysis approach to object recognition based on radon and Fourier－Mellin transforms［J］.Pattern Recognition，2007，40(12):3503－3508.

［13］蘇開娜，劉玉棟，馬麗.身份識別中步態特征的提取［J］.北京工業大學學報，2005，31(4):388－393.