前體渦誘導機翼搖滾擾動控制高速風洞試驗研究

陶 洋，趙忠良，王紅彪，楊海泳，郭秋亭

(1. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，四川 綿陽 621000； 2. 中國空氣動力研究與發展中心 高速空氣動力研究所，四川 綿陽 621000)

0 引 言

大迎角下翼身組合體將會出現繞體軸搖滾的非線性運動現象，人們稱之為機翼搖滾( Wing rock) 。該現象的出現不僅限制了以翼身組合體為基本氣動布局的現代飛行器的飛行包線，而且嚴重影響其大迎角飛行的機動操縱性能。因此機翼搖滾特性研究成為眾多空氣動力學研究學者的興趣之一。多年以來研究結果表明［1-3］：引起翼身組合體搖滾重要的原因之一是前體非對稱渦的誘導作用； Ericsson［3］認為翼身組合體機翼搖滾本質上是由前體非對稱渦和翼面的相互作用產生的，機翼只是簡單地提供了產生驅動搖滾運動的滾轉力矩所需力的作用面。這種作用在亞臨界雷諾數區尤為明顯。最近，鄧學鎣、馬寶峰對低速亞臨界雷諾數條件下前體渦誘導機翼搖滾運動的確定性進行了研究，發現模型頭部設置人工擾動對前體非對稱渦誘導的機翼搖滾特性影響起主控作用；同時發現當人工擾動位于φ=90°/270°附近時，模型搖滾呈現雙極限環搖滾運動狀態，通過流態顯示研究發現這種運動形態的發生主要由于在這兩個位置的頭尖部擾動能夠明顯促成左右渦系的隨機切換所引起。

在臨界雷諾數下，翼身組合體前體渦是否是誘導機翼搖滾的主要因素? 通過模型頭部設置人工擾動能否對前體非對稱渦誘導的機翼搖滾進行控制? 針對這一問題開展了前體渦誘導極限環搖滾流動的控制研究。采用翼身組合體模型大迎角下的搖滾特性進行了自由滾轉試驗，主要針對不同位置、不同顆粒大小、不同馬赫數下頭尖擾動對搖滾的控制效果開展研究。

1 試驗設備和模型

1.1 風洞

本次試驗是在氣動中心高速所的FL-23 風洞中完成的。FL-23 風洞是試驗段橫截面為0.6m ×0.6m的直流暫沖式亞、跨、超聲速風洞。試驗馬赫數范圍為0.3 ～4.5，馬赫數控制精度為±0.005。迎角范圍為-10° ～50°，試驗段上下壁面為開孔率4.2%的60°斜孔壁，兩側為實壁［4］。

1.2 模型

試驗模型為翼身組合體模型。模型直徑50mm，模型全長504mm，模型展長281.4mm，采用鋼質材料加工。模型迎角為0°時在風洞中的堵塞度約為0.6%，模型迎角為30°時在風洞中的堵塞度約為3.2%。

模型示意圖以及其在風洞中安裝情況見圖1。

圖1 試驗模型Fig.1 Models of test

1.3 其它設備

自由搖滾裝置采用精密機械球軸承支撐，通過聯接裝置與單支臂大迎角機構相連，通過12 位絕對式軸角編碼器來測量模型的角位移，測量精度可達0.088°，支撐裝置中的微型電磁離合器用于控制模型的鎖定及釋放，實驗數據的采集由PXI-4472B 動態信號采集模塊完成，最高采樣頻率為100K。

數據處理公式如下： 以平均滾轉角、滾轉角均方根、搖滾頻率來表征自由搖滾運動的3 個量，其具體處理公式如下，

平均滾轉角：

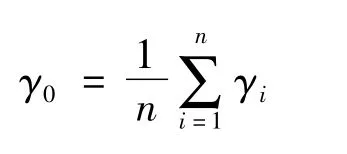
滾轉角均方根：

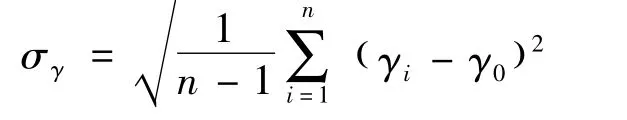
搖滾頻率： f

2 試驗結果與討論

試驗中得到了包括不同的頭尖部擾動位置、不同迎角、不同擾動顆粒大小的翼身組合體模型滾轉控制特性。試驗馬赫數范圍為0.3 ～0.6，迎角范圍為20°～45°，相應雷諾數范圍為3.25 ×105～6.25 ×105，處于臨界雷諾數區域。

圖2 中給出了馬赫數0.4 時無控翼身組合體在不同迎角下的搖滾特性，從圖中所示可見，搖滾主要發生在α=30°和α =35°兩個位置，α =30°時搖滾運動的滾轉角均方根較大，可以達到28°左右，搖滾頻率約4.5Hz，α =35°時搖滾運動的滾轉角均方根為20°左右，搖滾頻率約5.8Hz，在其余迎角條件下受風洞氣流湍流度等不確定條件的影響存在小幅振蕩。

2.1 頭尖擾動控制對翼身組合體搖滾特性的影響

尖拱旋成體前體渦對翼體搖滾的形成具有重要的影響，所以我們考慮通過對前體渦的控制來抑制翼體搖滾的發生，為保證前體渦及機翼搖滾運動形態的確定性［10］，在頭部粘貼陶瓷小球作為人工擾動。其在翼身組合體頭尖部黏貼方式以及周向角定義如圖3 所示( 前視) 。

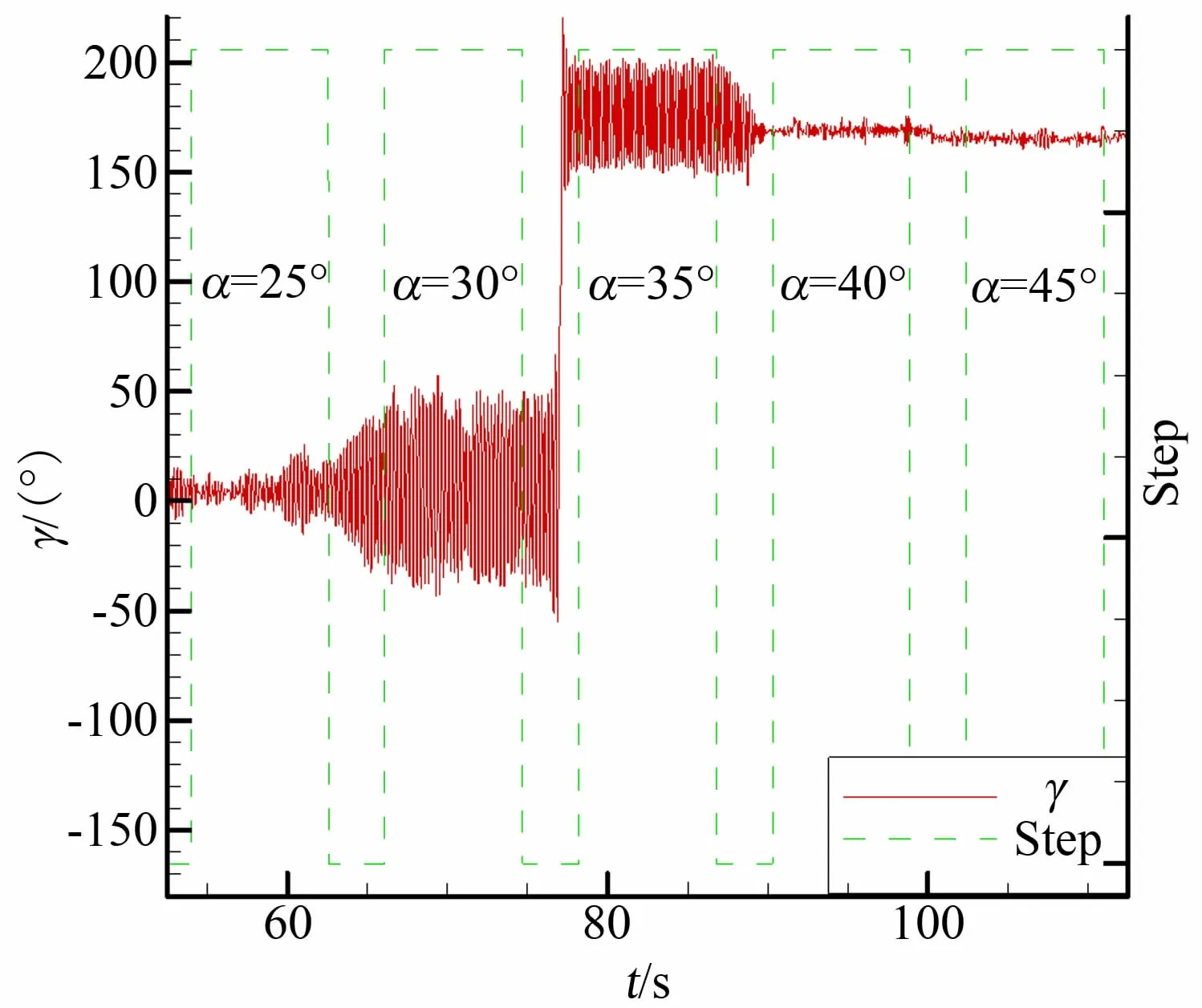
圖2 無控試驗結果Fig.2 Test data without control

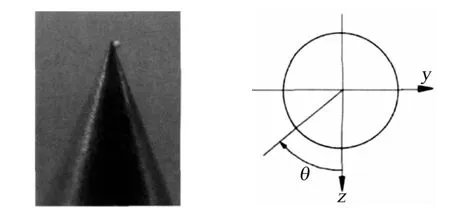
圖3 頭部擾動及其相對機身的周向角定義Fig.3 Tip perturbation and the azimuth angle relative to body axis

研究發現通過在頭尖部添加擾動以控制前體渦非對稱性的方式可以有效控制翼體搖滾的發生，但是添加擾動的周向位置對控制效果有明顯的影響。圖4 給出了不同頭尖擾動周向控制位置對搖滾振幅控制效果，圖5 給出了3 個典型的擾動位置有控自由搖滾時間歷程。從圖4 可見，正上和正下方的擾動基本對搖滾控制不起作用，在兩側正側方的擾動對搖滾抑制作用最強，基本可以完全抑制搖滾的發生，這一點從圖5( b) 有直觀的顯示，而斜上方和斜下方的控制有一定的效果但是沒有達到完全抑制搖滾的作用，斜下方的擾動控制效果要比斜上方控制效果稍好，α =30°時的控制效果要比α=35°時的控制效果好。

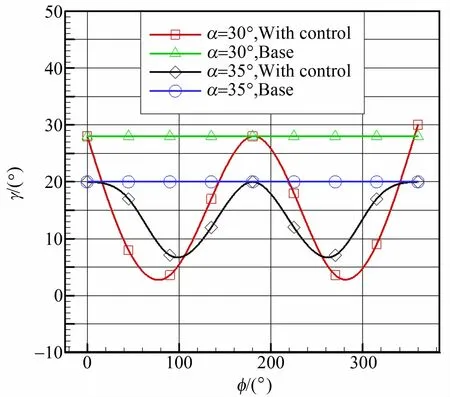
圖4 不同頭尖擾動周向控制位置對搖滾振幅控制效果Fig.4 Control effect of wing rock amplitude with tip perturbation control at different azimuth angles

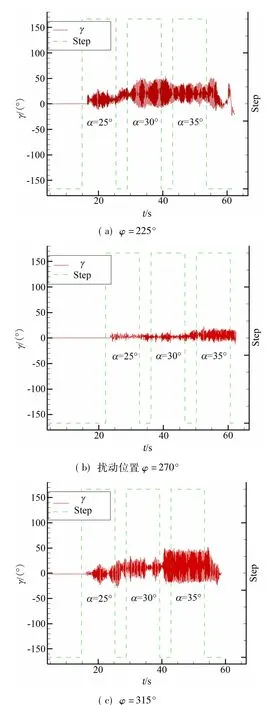
圖5 有控自由搖滾時間歷程Fig.5 Hisotry of free to roll with control

表1 和表2 分別給出了α=30°和α=35°不同周向位置搖滾控制效果，具體包括對平衡滾轉角、振幅滾轉角均方根以及搖滾頻率的影響，由于篇幅的限制給出了前視靠右側的控制結果，左側結果與右側控制效果類似，從表中可見右側的擾動使平均滾轉角有一個向右側的偏轉，量值大約在8° ～15°之間，這說明擾動的添加會使這一側的前體渦減弱或者抬升，從而降低了這一側機翼背風面的負壓絕對值，所以這一側的機翼有一個向下的滾轉趨勢。從搖滾頻率上來看只在兩側的擾動對頻率有較明顯的影響，使搖滾頻率增加了大約1Hz 左右，主要是由于左右兩側對搖振幅具有明顯的抑制作用所致。

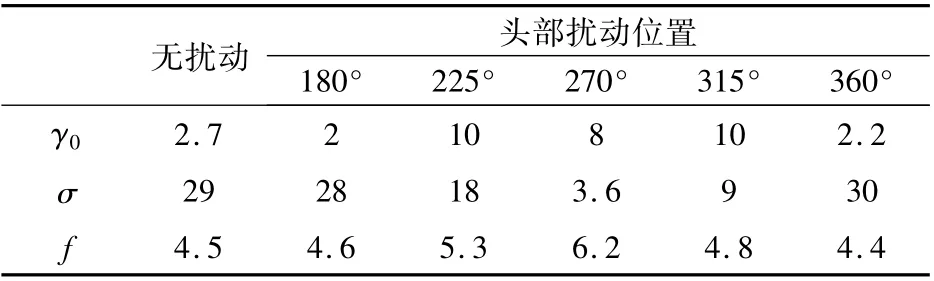
表1 不同周向位置頭尖擾動控制效果(α=30°)Table 1 Control effect with tip perturbation at different azimuth angles (α=30°)

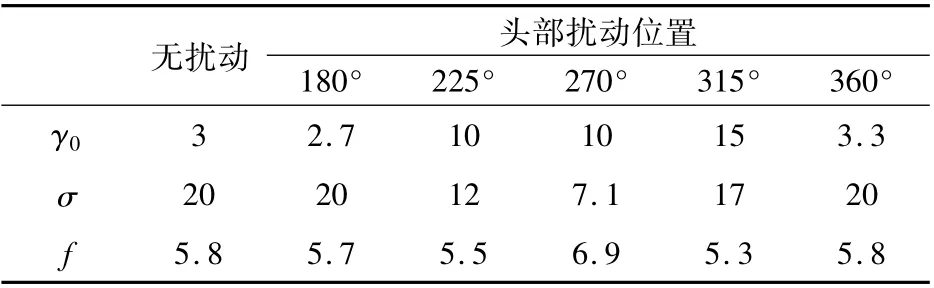
表2 不同周向位置頭尖擾動控制效果(α=35°)Table 2 Control effect with tip perturbation at different azimuth angles (α=35°)

從上面的研究可以知道單側的擾動會帶來平均滾轉角的偏移，所以嘗試了兩側擾動的方式來控制搖滾，結果顯示這種控制方法不僅能夠有效地控制搖滾的發生而且對平均滾轉角的偏移也有較好的控制效果。這也驗證了頭尖部的擾動控制機翼背風面的旋渦結構和強度有較大的影響。

在φ =270°位置嘗試了3 種不同直徑的陶瓷顆粒作為頭尖部擾動，分別為D = 1. 58mm，1mm，0.6mm，結果發現不同直徑的擾動源均能夠對搖滾起到明顯的抑制作用，擾動顆粒需要盡量往頭尖部靠近，最好與尖拱體相切，位置向后移控制效果減弱，如后移超過3mm 對模型搖滾特性基本沒有控制作用。

進一步開展了M =0.3、0.5、0.6 狀態下的搖滾控制試驗。研究結果表明： 在這些馬赫數下，通過頭尖擾動依然可以有效抑制前體渦誘導的翼身組合體搖滾。M=0.6 時控制效果對比如圖6 所示。

2.2 翼體搖滾控制機理分析

圖7 給出了翼身組合體一個典型翼體搖滾過程中力矩的遲滯曲線，呈現典型的雙“8”字形狀，由圖可見：翼體搖滾形成需要的兩個條件為回復機制( 主要存在于大滾轉角條件) 與偏離機制( 主要存在于滾轉平衡角附近) ，偏離機制主要由于流動相對于運動的滯后有關，在宏觀上表現為滾轉阻尼為負，而頭部擾動的加入主要是破壞了前體渦的結構，從而進一步消除了隨模型轉動引起的流動滯后效應，從而達到了抑制搖滾的效果。

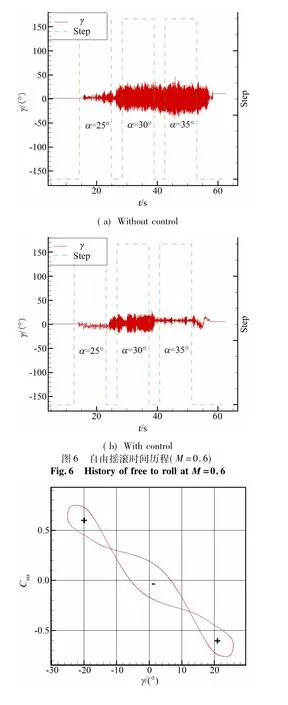
圖7 翼體搖滾滾轉力矩遲滯曲線( M=0.4，α=35°)Fig.7 Surface pressure and space flow at M=0.4，α=35°

圖8 給出了瞬時的物面壓力系數及空間流態，由圖可見模型頭尖部在大迎角狀態下明顯存在一組前體渦，翼身組合體搖滾由前體渦的不對稱性所觸發，由前體渦與機翼渦互相耦合形成的復雜渦系發展，由不同滾轉位置正負相間變化的滾轉阻尼維持。機翼迎風面在整個搖滾運動中均起抑制作用，前體渦與機翼渦組成的復雜渦系的位置、強度的滯后對機翼搖滾起促進作用。

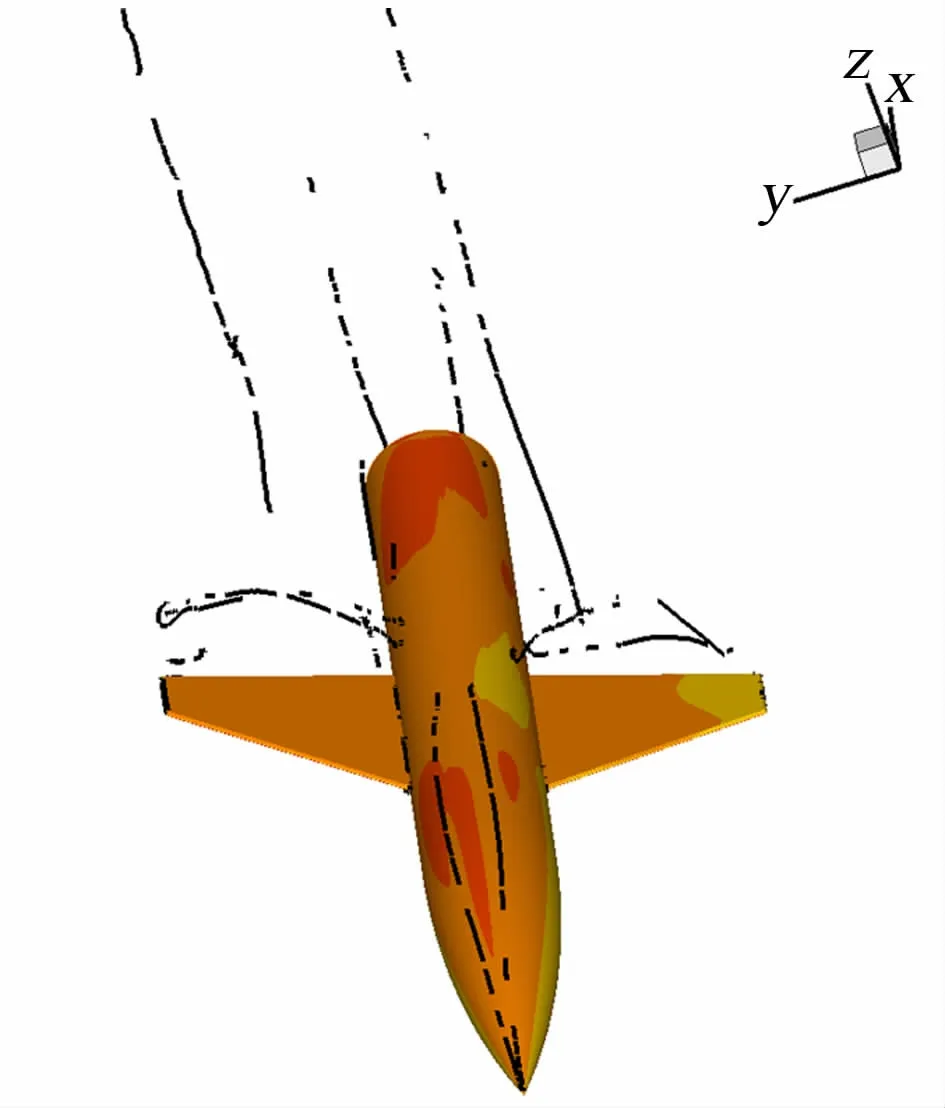
圖8 物面壓力機空間流態( M=0.4，γ=20°，α=35°)Fig.8 Surface pressure and space flow at M=0.4，γ=20°，α=35°

3 結 論

通過前體渦誘導機翼搖滾的擾動控制試驗研究可以得出以下結論：

(1) 通過頭尖部的小擾動可以影響前體渦從而進一步控制機翼搖滾特性；

(2) 側向位控制效果最好，斜側位的控制效果稍差，上下位基本沒有控制效果；

(3) 在頭尖部位置，擾動源的大小對搖滾控制效果沒有明顯的差異；

(4) 在試驗馬赫數范圍內，前體渦的控制均對搖滾起到抑制作用。

［1］ Katz Joseph. Wing/vortex interactions and wing rock［J］.Progress in Aerospace Sciences，1999，35： 727-750.

［2］ Nelson Robert C，Pell Etier Alain. The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers［J］. Progress in Aerospace Sciences，2003，39： 185-248 .

［3］ Ericsson L E. Wing rock generated by forebody vortices［R］. AIAA Paper 87-0268.

［4］ Alain Pelletier. Dynamic behavior of an 80/65 double-delta wing in roll［R］. AIAA-98-4353.

［5］ 伍開元. 面向先進飛行器設計的非定?？諝鈩恿W［J］. 流體力學實驗與測量，1997，11(2) ： 14-18.

［6］ 樊開導. 0.6m×0.6m 跨超聲速風洞性能與使用［R］.CARDC-2，1990.

［7］ Trickey C M，Edwards J A，Shaw S. Experimental and computational assessment of the dynamic stability of a supersonic square section missile［R］. AIAA 2004-5454.

［8］ 袁先旭. 非定常流動數值模擬及飛行器動態特性分析研究［D］. 中國空氣動力研究與發展中心，2002.

［9］ 劉偉，張涵信. 細長機翼搖滾的數值模擬及物理特性分析［J］. 力學學報，2005，37(4) ： 385-392.

［10］馬寶峰. 前體渦誘導機翼搖滾的實驗研究［R］. 博士后研究工作報告，北京航空航天大學，2007.