基于分形理論的宜興市蜀山古南街空間形態研究
郭雯雯,李早
(合肥工業大學建筑與藝術學院,安徽 合肥 230009)
1 分形理論的概述
1.1 分形理論的定義
1975年,美籍法國數學家曼德爾布羅特(B.B.Mandelbrot)出版了《分形對象——形、機遇和維數》(Fractal:Form,Chance,and Dimension,1975),開創了分形幾何學的先河。在其著作中闡述了“分形”的基本內容:形(From),即對象的形態;機遇(Chance),是隨機性或者說偶然性;維數(Dimension),則是用來描述對象不平整度、復雜度和卷積度的特征量,直接反映了對象的生成機制和構造方法。所謂“分形”,即是一些部分與整體以某種方式相似的形體,而描述分形的集合,即被稱為分形幾何。
1.2 分形維數
維數英文為“Dimension”,“幾何學上指空間獨立而互相正交的方位數通常的空間有三維,平面或曲面有二維,直線或曲線只有一維”(見《高級漢語大詞典》)。而分維又被稱為分形維或分數維,是作為分形的定量表征和基本參數而存在的。
在歐式幾何的概念里,點、線、面、體分別對應的維數是零、一維、二維、三維,愛因斯坦在相對論中引入時間維,則又形成了四維時空。然而,當面對著的對象是自然界里的客觀事物,則很難用具體的整維數來對其進行描述。

圖1 蜀山古南街總平面圖分形維數計算
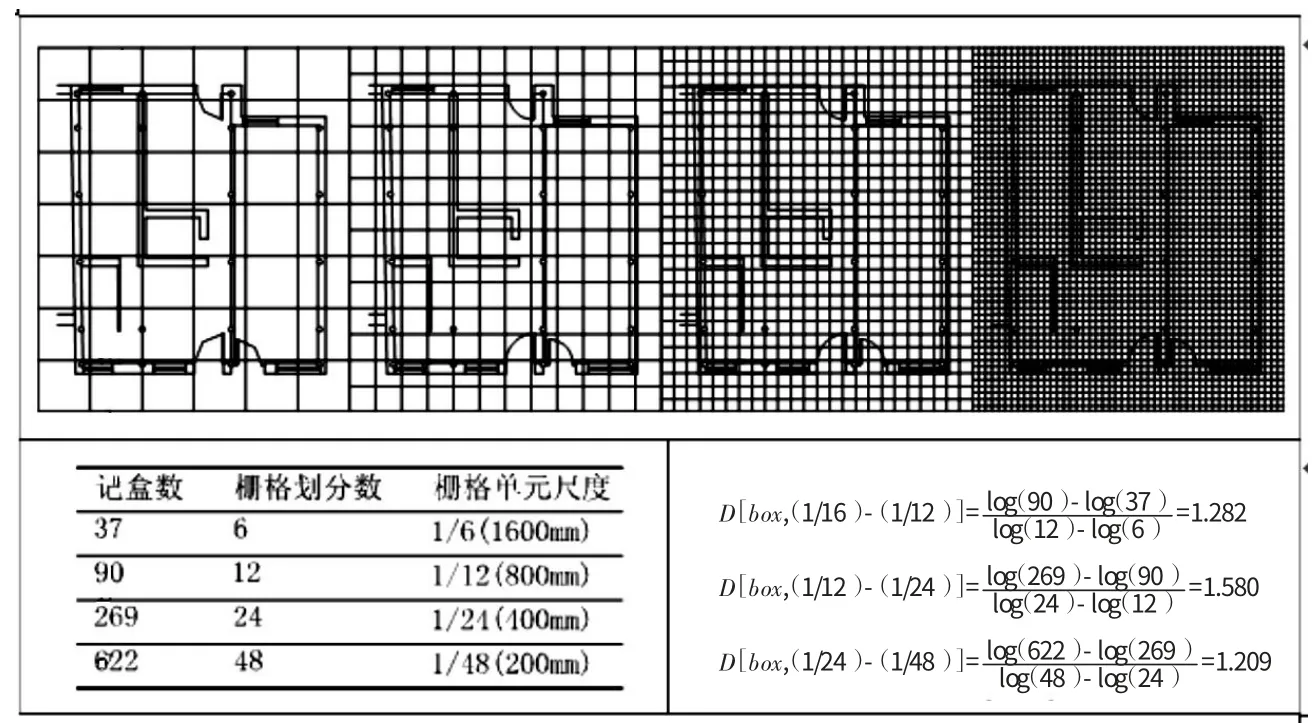
圖2 蜀山古南街167 號民居平面分形維數計算

圖3 蜀山古南街128 號民居立面分形維數計算
但是自然界事物中的自相似性也是不容忽略的,就好比一棵大樹主要是由樹枝和樹葉組成,若取下一根樹枝與整體樹干相對比,在構成形式上仍然是由分叉出來的細枝條與樹葉組成,仍然具有大樹的構成特點。雖然這種相似性并不能無限的擴展下去,但在一定尺度上來看,樹枝與樹枝之間,樹葉與樹葉之間,甚至細微到樹葉的葉脈,都具有這種明顯的自相似性。
由此可見,自然界中的分形,其實是在統計意義下的自相似性,并不是十分嚴格。凡是滿足統計自相似性的分形稱之為無規分形,另外,還有按一定的數學法則呈現,具有嚴格的自相似性的所謂有規分形。
1.3 計盒維數
在分形幾何中,計盒維數是一種測量距離空間中分形維數的計算方法,又稱為盒維數。要計算分形S的維數,可以想象一下把這個分形放在一個均勻分割的盒狀網格上,數一數這個分形所占的網格數。通過對網格的逐步精化,查看所覆蓋數目的變化,從而計算出計盒維數。
假設當劃分所形成的網格的邊長是ε 時,總共把空間分成N個網格,那么計盒維數就是:
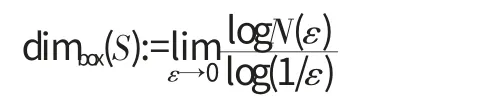
因此,本文將采用計盒維數的計算方法,通過對大尺度界面的擠壓,對宜興市蜀山古南街傳統古建聚落的空間形態及民居建筑的平立面形式進行科學定量化的研究。
2 分形理論用于蜀山古南街傳統古建聚落分析
2.1 古南街整體空間形態研究
蜀山區域現有的古南街是宜興現存最為完整的明清古街道,而對于分形特征的分析,筆者同樣是以計盒維數的方法對其總平面進行分形維數的計算。
根據宜興市蜀山古南街傳統古建聚落的規模,分別選用的柵格單元尺度為50m、25m、12.5m、6.25m。當柵格尺度為6.25時,所圍成的單個格子面積在40㎡左右,相當于一個小型民居建筑的基底面積,因此,可較為準確和有效的反映出古南街古建聚落各層級間的自相似程度見圖1。
如圖1所示,計算所得宜興市蜀山古南街總平面的分形計盒維數分別為1.263、1.634、1.732。由此可以看出,蜀山古南街古建聚落的整體空間形態,在不同柵格劃分層級上的分形維數也存在有較大的差異,各個分形層級在復雜程度上連續性較差,沒有明顯的分形特征。
蜀山古南街歷史文化街區總長達千余米,面積約4.6hm2,目前古建筑保存較為完好的地段長逾370m。這一街區在明清時期是陶都宜興最繁華的街區之一,這里近半的居民從事紫砂生產和經營,其住宅后屋為制陶作坊,臨街前屋則擺起貨架設店營銷,主街有多條支巷通向蠡河岸邊,而臨蠡河一面則由于水道的四通八達因此成為運輸船只停泊交易之所,形成了特色鮮明的陶都紫砂街。
但由于上世紀60年代開始,陸上交通的不便,導致商業慢慢冷淡下來,宜興市蜀山古南街傳統古建聚落日漸衰落。80年代后至今,多數居民的離開,民居人遷屋毀,蜀山古南街日益蕭條,便漸漸蛻變成安寧老舊的生活街區。
因此,宜興市蜀山古南街古建聚落的總平面圖的分形維數在數據上,則表現為大尺度柵格下分形維數較低和小尺度分形維數較高。
2.2 古南街民居建筑分形特征
2.2.1 建筑平面分形特征
宜興市蜀山古南街的建筑單體平面總體呈現出規整的矩形,其較短的一面經常面對街巷或者河道。依據建筑單體占地面積的多少,可將其分為小型建筑、中型建筑及大型建筑。
在此,筆者選取了蜀山古南街167號民居(經東南大學項目組測繪),同樣是以計盒維數的方法來分析建筑單體的平面形態。由于167號民居在尺度大小上,屬于中小型建筑,因此,選取的柵格單元尺度分別為1.6m、0.8m、0.4m、0.2m。柵格單元的尺度與民居內部空間的尺度相適應,也增加了理論分析的準確性見圖2。
如圖2所示,計算所得的分形計盒維數分別為1.282、1.580、1.209,由此可見,蜀山古南街167號民居的平面形態,在不同柵格劃分層級上的分形維數有所差異。從數據結果中,看出167號民居在一定程度上延續了古南街空間形態的分形特征,小尺度和大尺度的分形維數與整體空間的分形維數較為接近,中間尺度的分形維數較高。出現這樣的結果,則表明了建筑在單體空間的形態上略顯單一,建筑構成過于簡單,復雜程度略顯不足,因此并沒有像整體空間形態般呈現出明顯的分形特征。
2.2.2 建筑立面分形特征
傳統古建聚落有其特質性的美,在各平面、立面的構成元素中,都蘊含著形式與尺度的層次性與和諧性。
在對宜興市蜀山古南街單體建筑的立面研究中,筆者以128號民居為例,做建筑立面的分形分析,從三維立體的角度解析古建聚落不同的特質性空間。結合之前單體建筑平面的分析結果,選取2m為柵格單元尺度,依次劃分為2m、1m、0.5m、0.25m(見圖3)。
如圖3所示,計算所得的分形計盒維數分別為1.737、1.548、1.711,這表明了宜興市蜀山古南街128號民居的立面在各個柵格劃分的層級上總體都有較高的分形特征,層級復雜程度的連續性較好。大尺度和小尺度的分形維數基本接近而中間尺度卻略低,則說明了各層級之間的相似性高,但建筑立面尺度層級仍存在缺失。
3 結 語
通過分形理論的研究與運用,可以發現在宜興市蜀山古南街傳統古建聚落的空間形態和整體布局上有著較明顯的自相似性,這也是建筑群所顯著的分型特征。雖然古代建筑講究師法自然,但建筑畢竟不是大自然中的花草樹木,并不是自然形成的,因而它所表現出來的這種自相似特征受到社會以及人們行為的影響。
這種建筑自身所呈現出來的自相似性,也是一種自然屬性,也說明了在經年累月的發展和變化中,古建聚落基本上是在以一種自然而不被束縛的軌跡前進,延續著自身所固有的文化和脈絡。
[1] 陳颙,陳凌.分形幾何學[M].北京:地震出版社,1998.
[2] 冒亞龍,何鏡堂.分形建筑審美[J].華南理工大學學報(社會科學版),2010(4).
[3] 祁崢.宜興蜀山古南街柔性節點空間淺析[J].山西建筑,2010(30).
[4] 冒亞龍,雷春濃.生之有理、成之有道——分形的建筑設計與評價[J].華中建筑,2005(2).
[5] 陸志鋼.江南水鄉歷史城鎮保護與發展[M].南京:東南大學出版社,2001.
[6] 江蘇省宜興市丁蜀鎮志編委會.江蘇省宜興市丁蜀鎮志[M].北京:中國書籍出版社,1991.
[7] 趙遠鵬.分形幾何在建筑中的應用[D].大連:大連理工大學,2003.
[8] 孫博玲.分形維數(Fractal dimension)及其測量方法[J].東北林業大學學報,2004(3).
[9] 張云飛.宜興蜀山古南街民居的模糊空間研究[D].無錫:江南大學,2009.

