煉廠自備碼頭港口吞吐量預測分析

中國石油大連分公司 李玉猛

一、自備碼頭港口吞吐量

港口吞吐量是港口最基本的生產指標，是組織港口生產、編制港口發展規劃和進行港口建設的依據。同時港口吞吐量的大小可以反映港口所在城市及其腹地范圍內的經濟狀態和發展水平，吞吐量的貨物分類可以反映港口所在城市及其腹地范圍內的產業結構和經濟結構，吞吐量的進出口流向可以反映港口之間、城市之間、地區之間、外貿港口的國家之間等的經濟和貿易關系。港口吞吐量發展是受到諸多客觀因素影響和制約的,其預測成果的準確度、可靠性受人為主觀因素的影響也是明顯和直接的。

煉廠自備碼頭作為貨主碼頭的一種形式，其港口吞吐量是所在城市港區吞吐量的重要組成部分。煉廠自備碼頭港口吞吐量的發展變化很大程度上取決于煉廠的原油加工能力以及煉廠實際原油加工量的發展變化，集中反映煉廠的運營狀態，在一定程度上也反映了所在地區的經濟運行狀態。同時，隨著煉廠本身不斷增加從海上進口原油的加工量，港口吞吐量的發展又影響著煉廠的原油加工量。因此，一般的預測方法很難科學合理的對煉廠自備碼頭港口吞吐量的未來發展趨勢進行預測分析，必須同時考慮到煉廠原油加工量和港口吞吐量的相互影響和制約才能做出準確預測。

為了能夠準確把握煉廠自備碼頭港口吞吐量的發展趨勢，并為進一步對碼頭通貨能力與煉廠原油加工能力的匹配性進行評價提供基礎數據，本文分別運用灰色理論GM(1,1)模型和MGM（1，n）模型對某北方煉廠自備碼頭的港口吞吐量進行預測，進行比較分析。

二、GM(1,1)模型和MGM（1，n）模型

(一)GM(1,1)模型簡介

灰色系統理論是我國學者鄧聚龍教授的首創，GM(1,1)模型是最常用的一種灰色系統模型，通過單變量的一階微分方程模型揭示其內在發展規律，用于單一時間序列的建模和預測。

其解的離散描述形式為：

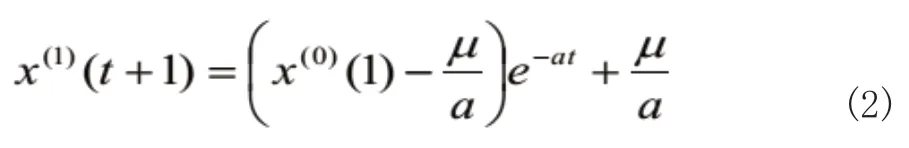
確定了參數a 和μ后，按照此模型類推即可得到預測的累加數列。通過驗證后，再累減還原得到預測值。

預測步驟如下：

1.由原始數列x(0)按照下式計算累加生成數列x(1)：

2.采用最小二乘法，按下式確定模型參數

式中：

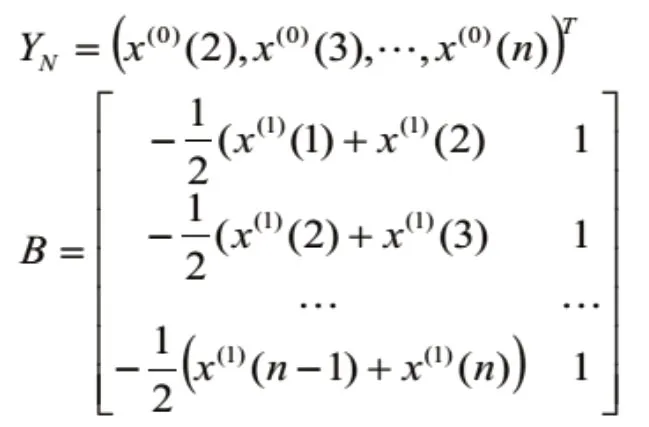
3.建立預測模型，利用(2)式求出累加數列。

4.采用殘差分析法進行模型檢驗，或用計算后驗差C和小誤差概率P 的辦法檢驗。

模型的精度分四級如表1 所示：

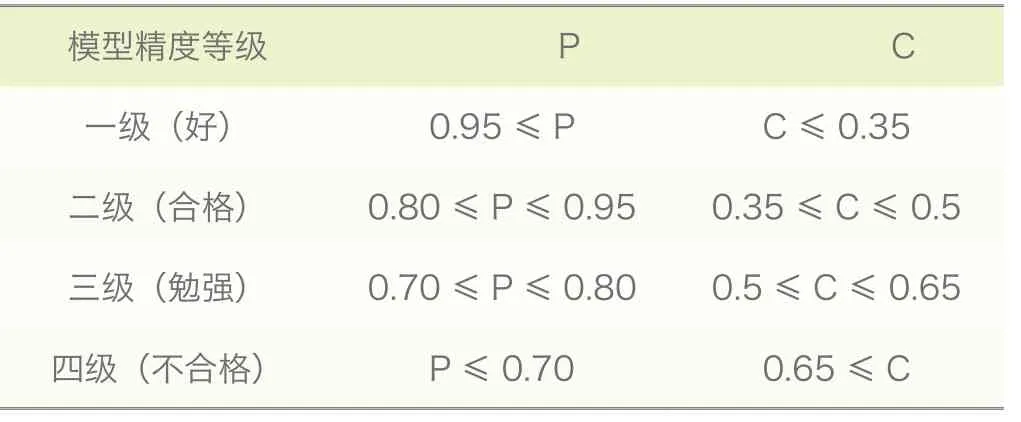
表1 灰色預測精度等級表

表中，

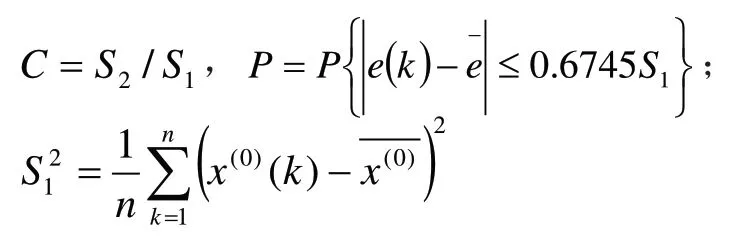
其中:

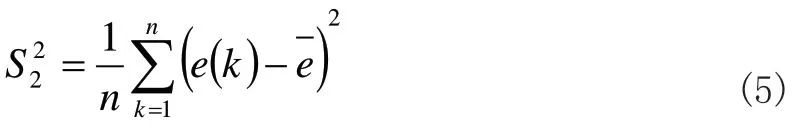
(二)MGM（1，n）模型

GM(1,1)模型是最常用的一種灰色系統模型，它通過單變量的一階微分方程模型揭示其內在發展規律，用于單一時間序列的建模和預測。然而實際社會、經濟系統中往往包括多個變量，各變量相互關聯、共同發展。這時，每一個變量的發展變化都不是孤立的，一個變量要受到其他變量的影響，同時也影響著其他變量。為此，本文采用多變量灰色模型——MGM（1，n）模型，旨在從系統的角度對各變量進行統一描述。MGM（1，n）模型的形式是n元一階常微分方程組，它是GM(1,1)模型在n元變量的情況下的自然推廣，不是GM(1,1)模型的簡單組合，也不同于GM(1,n)模型。具體原理如下：

其中，k=1, 2,…,m。

MGM（1，n）模型為n元一階常微分方程組：

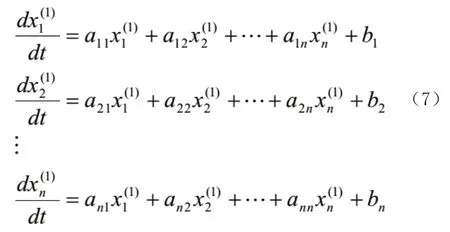
即：

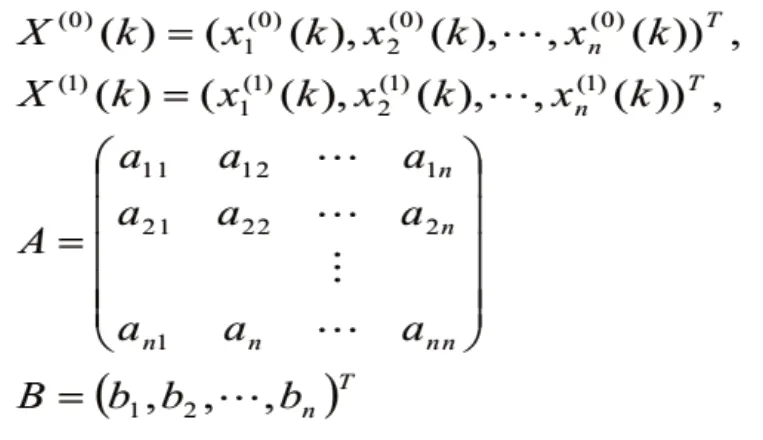
則（7）式可記為：

上式的連續時間響應為：

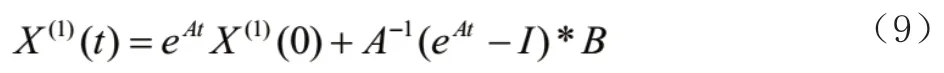
其中：

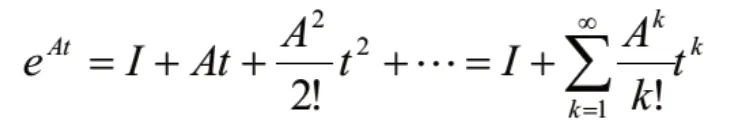
為了辨識參數A 和B，將（7）式離散化得到：

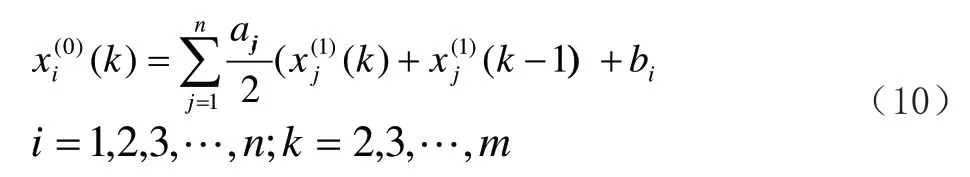
記ai=(ai1,ai2,…,ain,bi)T,i=1,2,…,n.。則由最小二乘法得到ai的辨識值。

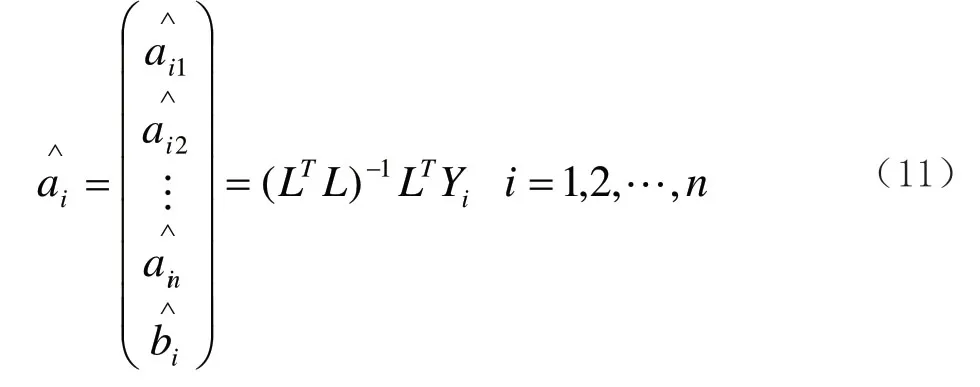
其中：

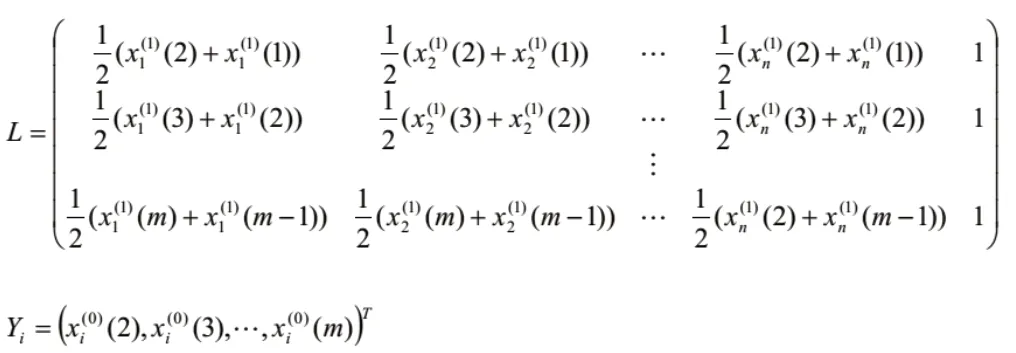
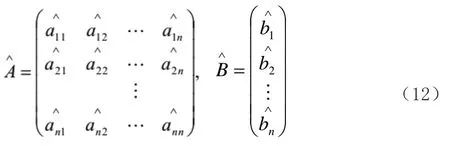
MGM（1，n）模型的計算值為：

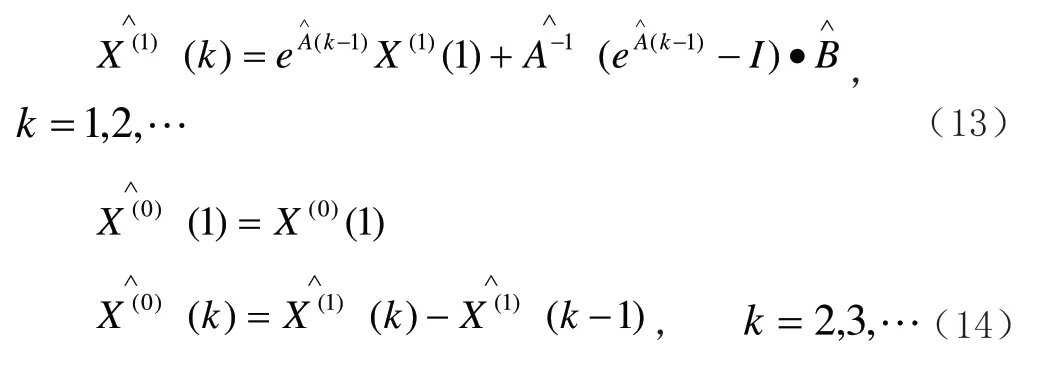
當n=1時，MGM（1，n）模型就退化為GM（1，1）模型；當B=0時，MGM（1，n）模型就是n個GM（1，n）模型的組合。由公式（9），（13）和（14）可知MGM（1，n）模型不僅可以建模還可以進行預測。

三、模型應用和比較

(一)煉廠自備碼頭的特點

某北方臨海煉廠作為國內規模最大的煉油基地之一，不僅具備優越的地理位置和區位優勢，而且具備完善的物流體系，如公路、鐵路、管道和港口等，其中港口作為物流手段之一卻承擔著該煉廠絕大部分的物流任務，該煉廠擁有5000 噸級至10 萬噸級的碼頭泊位15個，一直以來，20%以上的原油上岸和80%以上的產成品下海都是通過碼頭實現的。

某北方臨海煉廠2007—2013年的原油加工量和碼頭吞吐量如表2所示。

通過以上統計數據，實際分析煉廠自備碼頭的的吞吐量和加工量的發展變化有如下特點：

1.煉廠自備碼頭港口吞吐量的實現是以煉廠原油加工量的實現為必要條件，也就是說煉廠煉油越多，碼頭吞吐量越大。然而，煉廠原油加工能力在某一個階段內是一定的，是有上限的，原油加工量的發展變化不是永遠呈遞增趨勢，最終原油實際加工量將穩定在煉廠最大煉油能力極限值附近浮動，此時煉廠自備碼頭港口吞吐量最終也將趨于某一定值。因此，煉廠自備碼頭的發展、建設和未來規劃應當與煉廠煉能的擴能相匹配，共同發展。

2.煉廠自備碼頭港口吞吐量中原油進口量的增加在一定程度上不僅促進了煉廠煉量的增加，而且大大提高了港口自身的吞吐量，這一趨勢將隨著煉廠陸上原油供應量的逐年減少和海上原油供給量的逐漸增加而變得更加明顯。比如，2009—2010年度煉廠原油加工量和吞吐量的逆行變化就是因為當年原油通過海上進口量幾乎為零所造成的。

(二)模型計算和精度比較

利用MGM（1，n）模型得出的兩序列的MGM（1，2）模型狀態方程組為：

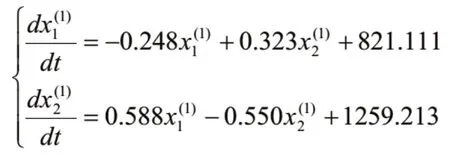
如對上述兩個數列分別建立GM（1，1）模型，則可以分別得出原油加工量和港口吞吐量的灰色狀態方程。

原油加工量的GM（1，1）模型為：

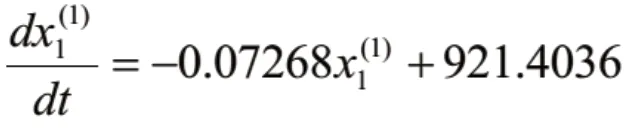
碼頭吞吐量的GM（1，1）模型為：

利用Malab 軟件龍格庫塔法求微分方程組，得出原油加工量和碼頭吞吐量兩個數列的累加數列，然后還原成原始數列就是每個年度原油加工量和碼頭吞吐量的MGM（1，n）模型預測值。同樣對于GM（1，1）模型，分別求解各自微分方程，得出原油加工量和碼頭吞吐量GM（1，1）模型預測值，比較如表3所示。

MGM（1，2）模型預測擬合圖如圖1所示：

GM（1，1）模型預測擬合圖分別如圖2，圖3 所示：

表2 某煉廠2007—2013年的原油加工量和碼頭吞吐量 萬噸

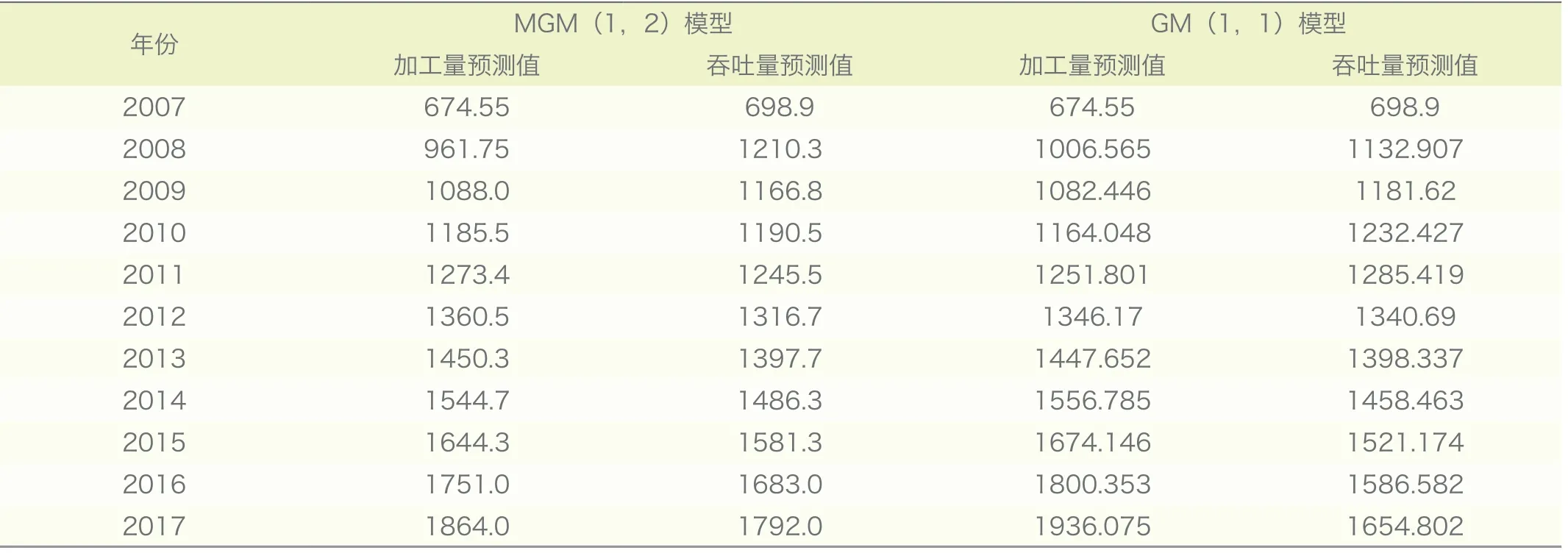
表3 GM（1，1）模型和MGM（1，2）模型預測值比較 萬噸

通過用計算后驗差C 的辦法檢驗，分別求得C 值參考

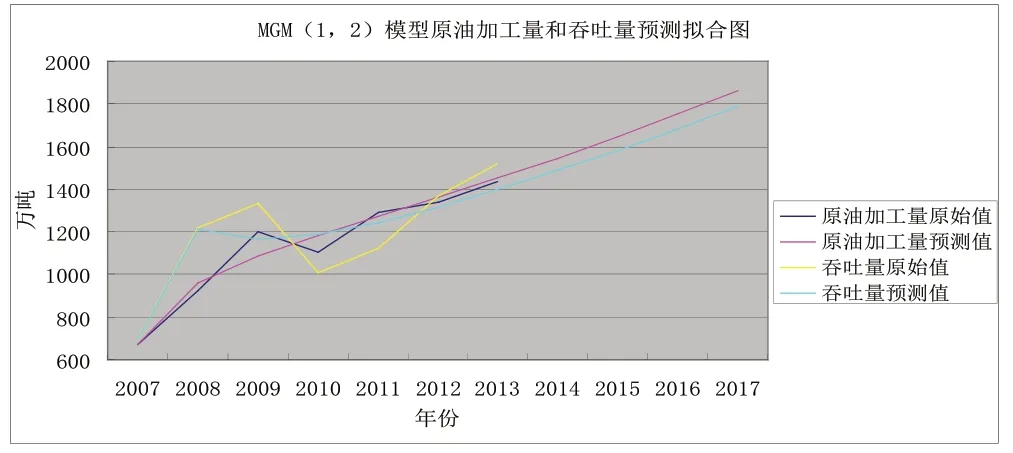
圖1 MGM（1，2）模型原油加工量以及港口吞吐量預測擬合圖

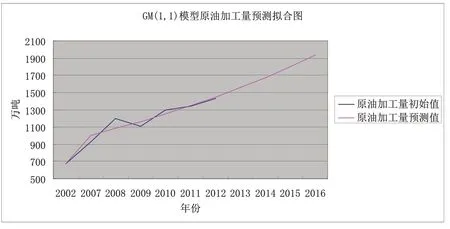
圖2 GM（1，1）模型原油加工量預測擬合圖

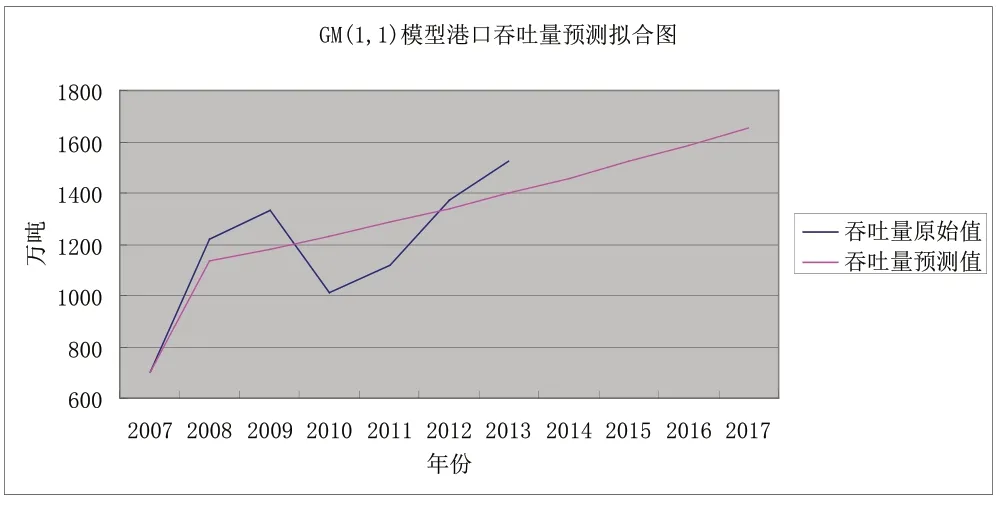
圖3 GM（1，1）模型港口吞吐量預測擬合圖

灰色預測精度表中的指標來判定原油加工量和碼頭吞吐量的預測精度，其中，MGM（1，2）模型原油加工量的C 值等于0.225，為一級精度；MGM（1，2）模型碼頭吞吐量的C 值等于0.459，為二級精度，均符合灰色模型關于預測精度的要求。

GM（1，1）模型原油加工量的驗差C 值等于0.247，為一級精度，符合灰色模型關于預測精度的要求，而 GM（1，1）模型碼頭吞吐量的C 值等于0.527，為三級精度，屬于勉強級別，如用于預測誤差較大，很難提供參考價值。

另外，從兩個模型的擬合圖比較來看，MGM（1，2）模型更優。

四、結語

從系統的觀點來看，MGM（1，n）模型是一種狀態模型，它是單變量GM（1，1）模型在多變量的情況下的自然推廣，旨在反映各變量之間相互制約、相互促進的關系。MGM（1，n）模型不能代替GM（1，1）模型，而是GM（1，1）模型的擴展和補充。同時，MGM（1，n）模型不同于GM（1，n）模型，是一種預測模型。

通過某北方臨海煉廠的實例，對該煉廠的原油加工量和港口吞吐量兩個變量建立MGM（1，2）模型，不僅預測煉廠在未來中長期原油加工量和港口吞吐量的發展變化趨勢，而且揭示了煉廠自備碼頭港口吞吐量和原油加工量的內在聯系。鑒于原油能源的稀缺性和不可再生性，世界上大多具有遠見的發達國家都不再開采煉制本國的原油資源，我國也深刻認識到這一點，年進口原油過億噸，并且進口依存度已經超過50%。因此，未來不僅沿海煉廠，甚至內陸煉廠都將可能全面煉制海外原油，那么具有自備碼頭的沿海煉廠只有在吞吐能力在達到煉油能力2 倍的條件下，方能滿足煉廠產能的實現以及原油上岸和產成品下海的雙重物流需求，屆時甚至會出現煉廠向碼頭要煉量的局面。基于這一點，煉廠自備碼頭在規劃建設過程中，未雨綢繆地預留一定的通貨潛能以待挖掘是合理的。

[1]劉思峰,郭天榜,黨耀國.灰色系統理論及其應用[M].北京：科學技術出版社,1999.

[2]鄧聚龍.灰色預測與決策[M].武漢：華中工學院出版社,1986.

[3]歐軼.預測港口吞吐量方法的探討[J].水運工程,2003（1）：22-25.

[4]馮英浚,翟軍,盛建明．MGM(1,n)灰色模型及應用[J].系統工程理論及實踐,1997（5）：109-113.

[5]顧光炎.對港口吞吐量統計制度改革的思考[J].港口裝卸.1995（4）:34-35.