基于不等間隔接收機鐘差組合預報模型的輔助定位方法

占建偉 ，吳鵬，龔航，彭競，歐鋼

(1. 國防科技大學 電子科學與工程學院，湖南 長沙，410073；2. 第二炮兵工程大學 四系，陜西 西安，710025)

在衛星信號受遮擋嚴重地區，例如城市高樓、停車場、隧道、室內，可能出現部分信號中斷或全部信號中斷情況。定義可見衛星僅有3顆的情況為“3-D不完備條件”，可見衛星數大于 4顆的情況為“完備條件”[1]。統計表明，“3-D不完備條件”以大于10%的概率頻繁出現，每次出現平均持續約為50 s[2]，這導致接收機首次定位時間和失鎖重捕時間大大增加，采用完備條件下的定位方法可能無法給出定位結果或者定位精度很差，嚴重影響BDS，GPS和Galileo等各類接收機的定位可用性和可靠性，使其應用范圍受到了極大限制。針對這一問題，往往通過集成傳感器引入外部測量信息輔助的方法降低對可見衛星數的依賴，以實現三維定位，如氣壓高度表、RFID，偽衛星、INS或者電子地圖匹配等方法[3?6]。但是，以上方法需借助外部設備，往往成本較大，作用范圍具有一定的局限性。不借助任何外部信息、完全利用接收機在非輔助條件下解算得到鐘差解算值，通過建立鐘差預測模型，預測未來所需某時刻的鐘差用于輔助定位的方法，實現簡單、靈活、性價比高。目前，已有若干文獻對接收機鐘差輔助建模及輔助定位算法進行了一定的研究[7?10]，但不夠成熟和全面。歸納起來，上述文獻所提出的方法主要有以下幾個特點：(1) 以往的研究往往集中于廉價原子鐘、恒溫晶振，缺少對廉價溫補晶體振蕩器(TCXO)的相關分析，而后者在許多接收機里很普及，盡管其長穩不如原子鐘理想，但是其50 s以內的短期穩定度一般可以達到10?9以上[1]；(2) 鐘差模型的建立采用的是等間隔的觀測數據，而城市典型環境下的信號中斷往往呈現間歇性的特點，用戶定位的連續性得不到保證，解算得到的鐘差解算值序列往往是不等間隔的；(3) 單一的鐘差預測模型有其自身的特點和適用范圍，對于不同的環境，單一模型的可靠性得不到保證，在實用上存在一定的局限性和缺陷。為了解決上述問題，本文作者利用非等間距接收機鐘差解算值序列，基于傳統的多項式模型和灰色模型，分別提出廣義延拓逼近法的改進多項式模型和改進非等間距灰色模型；并在此基礎上提出了一種動態加權組合預測模型及其相應的輔助定位算法。

1 鐘差預報模型建模

1.1 改進的多項式鐘差模型

設在城市遮擋環境中得到預處理后的不等間隔健康鐘差序列為x(t1)，x(t2)，…，x(tm)，其中ti?ti-1≠常數。根據鐘差的物理意義，一般采用多項式模型對接收機鐘差進行建模[11]。

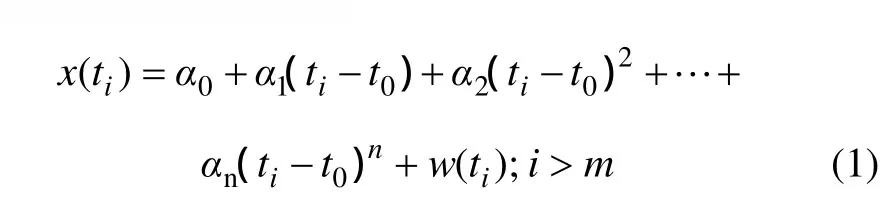
其中，α0，α1，α2，…，αn為待定的多項式模型參數，分別表示鐘偏、鐘速、頻率漂移等；n為模型的階數，可通過殘差確定，針對大多數接收機晶振，n=2時可滿足模型精度要求；t0為參考時刻，一般進行歸一化處理，即令t0=0；w(ti)由多種噪聲組成，主要包括相位噪聲和測量噪聲。

考慮到原點tn及附近的鐘差解算值對預測值影響最大，因此選擇約束在原點誤差最小的條件下，通過使殘差平方和達到最小值來確定α中各參數α0，α1，α2，…，αn，具體如式(2)所示。

其中：Hn為H矩陣的第n行構成的行向量。

式(2)可以采用拉格朗日乘子法進行解算[12]。

1.2 改進的不等間隔灰色模型

灰色 GM(1,1)模型廣泛應用于少數據、貧信息、不確定性問題的預測，在衛星鐘差的長期預報中具有一定的實用性[13]。而接收機鐘差與衛星鐘差一樣，受多種噪聲的影響，有些噪聲特性已經明確，有些噪聲特性未知或者不確定，符合灰色系統的特點，因此，本文嘗試將接收機鐘差序列視為灰色系統。

傳統的 GM(1,1)模型都是基于等間隔觀測數據建立的，并不能直接應用于非等間隔鐘差數據的預報，必須進行適當改進。相似問題在其他領域已經有一定研究，考慮到典型城市3-D不完備條件下接收機觀測數據少，線性化的特點，本文采用文獻[13]。中提出的改進模型AMUGM(1,1)。該模型的特點是通過優化背景值，擴大了模型的實用性，使其同時適用于具有線性變化和指數變化規律的數據序列預測，其鐘差預測值的表達式為

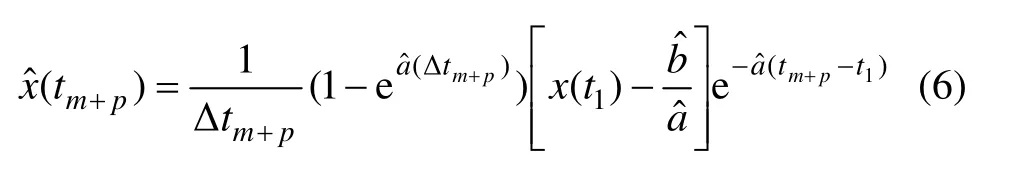
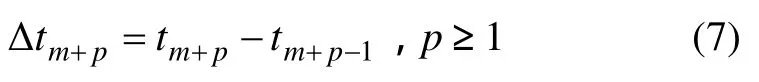
當m＞4時，利用最小二乘原理，可求得參數估計值為：

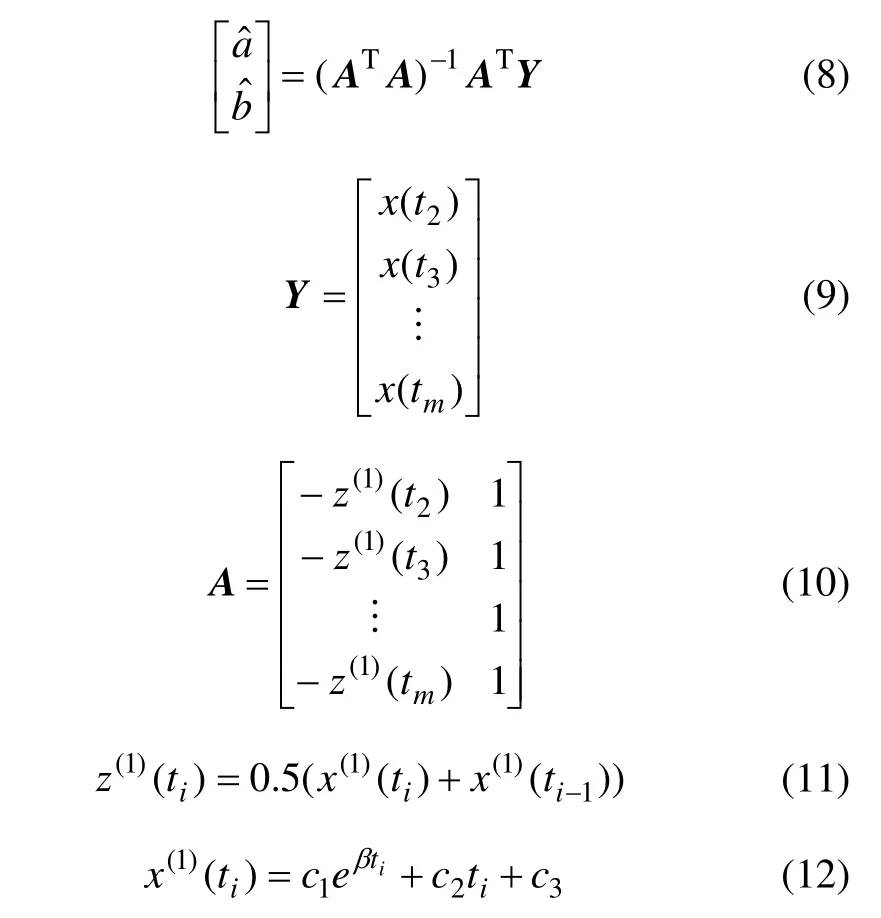
式中，x(1)(ti) 表示原始序列與時間間隔相乘后的一次累加序列，其累加關系如(13)所示；β，c1，c2，c3依據平均值和最小二乘原理求取。待確定各參數后，可以依據式(6)預測鐘差值。

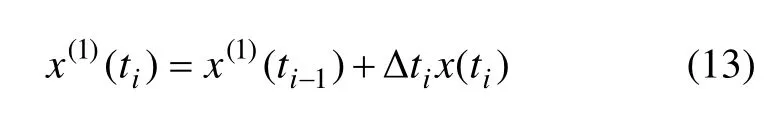
1.3 動態加權組合模型

任何單一的預報模型都有自身的特點和適用性。如多項式模型物理意義明確，短期預報效果好，而灰色模型在只有少量觀測數據情況下，長期預報也能保證預報的精度[11]。因此，應用組合方式是實現2種模型優勢互補的一種有效途徑。在各種組合模型中，加權線性組合模型被廣泛應用，該模型具有優化目標函數和優化準則建立及求解簡單、計算量小的優點。

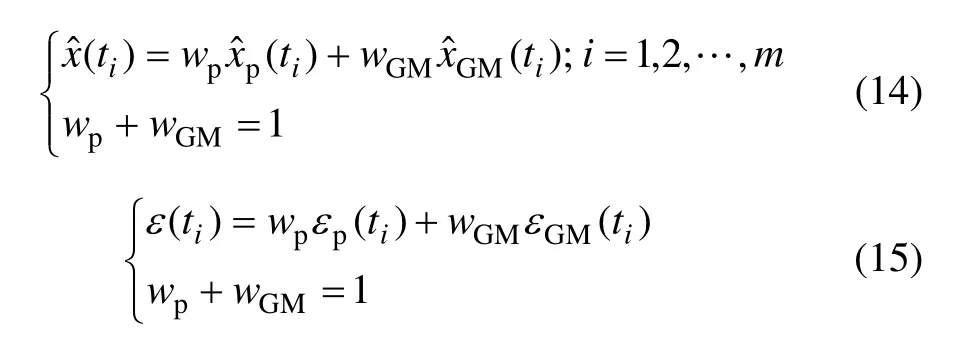
權值wp和wGM通過求解組合模擬誤差平方和最小值來確定，對應的優化目標函數如式(16)所示。同時定義ε，εp和εGM分別為對應觀測值組成的列向量，如式(17)～(19)所示。

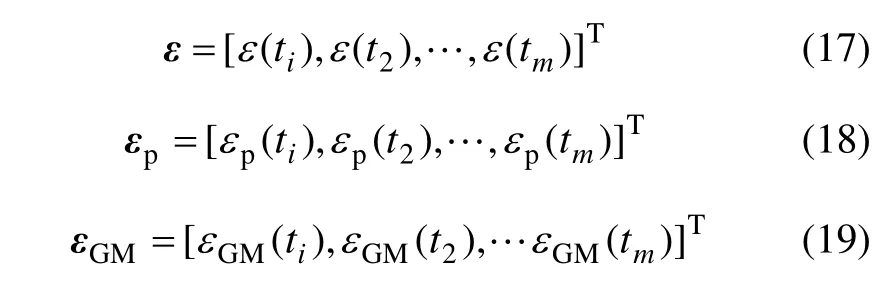
利用消元法和并將I對w求微分，易得到最優權值為wp。如式(20)所示。而wGM可依據式(14)的約束方程解算得到。

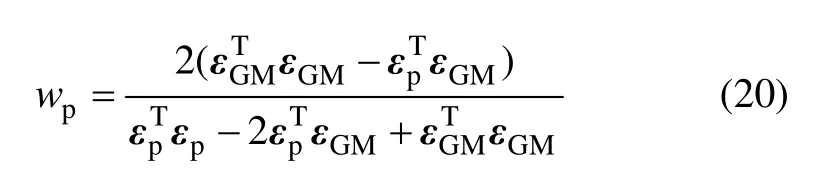
以上建立的模型可以用來預測短時內的鐘差，但是由于參數固定，其預測誤差會隨著時間增長而逐漸積累。因此，提出采用“滑動窗”來鎖定最新的鐘差解算值，同時剔除“最舊鐘差解算值”，然后重新估計模型參數。這樣，每次計算就只需要固定長度的最新觀測值，大大減小了存儲量，提高了運算速度。

1.4 模型短期預測能力評價標

建立組合模型后，選用的預測性能評價標準主要包括殘差平方s和平均相對誤差Δ，計算公式如下：

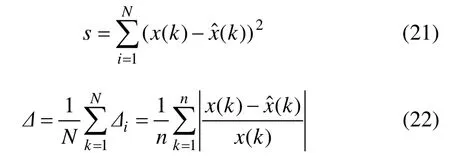
2 鐘差輔助定位算法

2.1 鐘差輔助的原理

依據鐘差組合預測模型外推預測得到接收機鐘差預報值，可建立如下約束方程用于輔助定位：

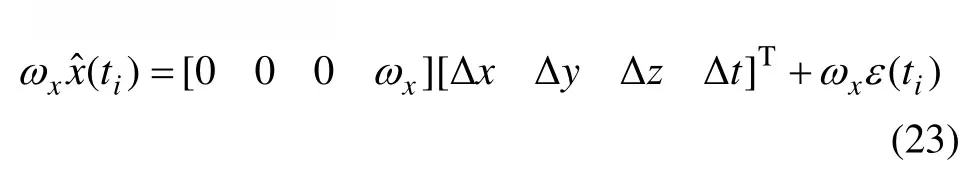
其中，ωx為偽距測量誤差標準差和鐘差誤差標準差的歸一化參數，用于調整約束方程(23)的誤差分量，使得調整后的誤差分量具有相同的方差。

將式(23)并入無任何輔助的基本定位方程組(25)，從而可完成3-D不完備條件下的輔助定位。

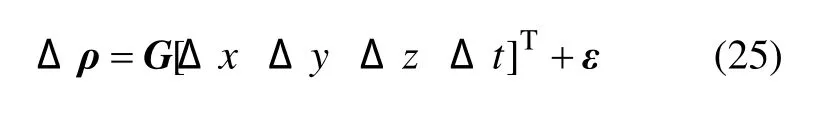
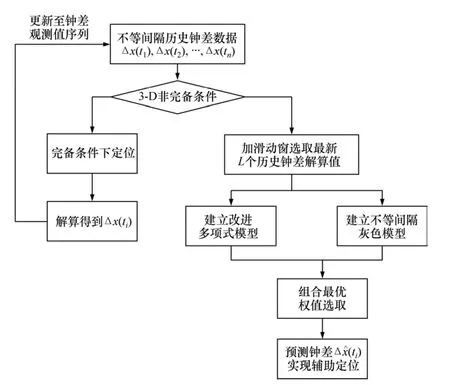
圖1 短時預報鐘差輔助定位算法Fig. 1 Flow of clock-aided positioning algorithm for short-term prediction

其中：Δρ為測量偽距值與偽距估計值之間的偏差；ε為偽距測量誤差矢量；G為n×4的觀測矩陣；n為可視有效衛星數。可以看出，基于鐘差輔助的定位算法實際上相當于增加了1顆觀測衛星，是解決3-D不完備條件下定位連續性和可用性的有效方法之一。

值得注意的是：針對短時預報得到鐘差預測值，在滑動過程中，不宜作為新息引入模型。原因是與正常解算鐘差值相比，鐘差預測值多了1項預測誤差。由式(26)可知，該預測誤差將引起額外的定位誤差。

2.2 接收機鐘差輔助的定位精度

在鐘差輔助定位中，鐘差預測模型的精度將直接影響最終的三維定位精度，其影響可采用式(26)進行評估[10]。而式(27)進一步表明，當鐘差預測值和實際鐘差之間的誤差σb大于時間精度因子(DTDOP)和衛星基準偽距測量均方差σs的乘積時，鐘差輔助定位的誤差比完備定位條件下的定位誤差大。

其中，H3為3×3的幾何觀測矩陣。

而在鐘差輔助定位中，σb應由2部分組成，模型預測值與實際鐘差解算值間誤差σp，以及實際鐘差解算值與真實鐘差間誤差σc。當預測模型為改進二次多項式模型時[8]，三者的關系可以表示為

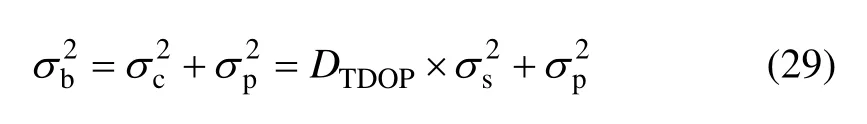
根據式(29)可知，σp作為鐘差σb的主要組成部分，將是影響輔助定位精度的主要誤差因素。因此，高精度的鐘差預報模型有利于提高定位精度。

3 試驗結果及討論

3.1 鐘差預報性能評估

3.1.1 鐘差數據合理性驗證

為了驗證鐘差預測模型輔助接收機定位解算的性能，于 2013?03?20在長沙某固定點采用北斗接收機進行靜態數據采集，采樣頻率為1 Hz，接收機記錄了各可視衛星的坐標、偽距、精度因子和接收機鐘差等觀測數據，時間起點對應的周內時間為265 151 s。其中，定位解算時采用的衛星偽距均方根誤差分別為：σGEO=6.5 m，σIGSO=4.5 m，σs=σGEO。

晶振的頻率穩定度在一定的程度上反映了鐘差的可預測性[1]。利用上述連續的鐘差解算值計算得到頻率穩定度，如圖2所示。 由圖2可見：實驗所得北斗接收機TCVCXO(CFPT-XXX)晶振50 s的頻率穩定度約為2.5×10?9，鐘差預測可以達到納秒級。

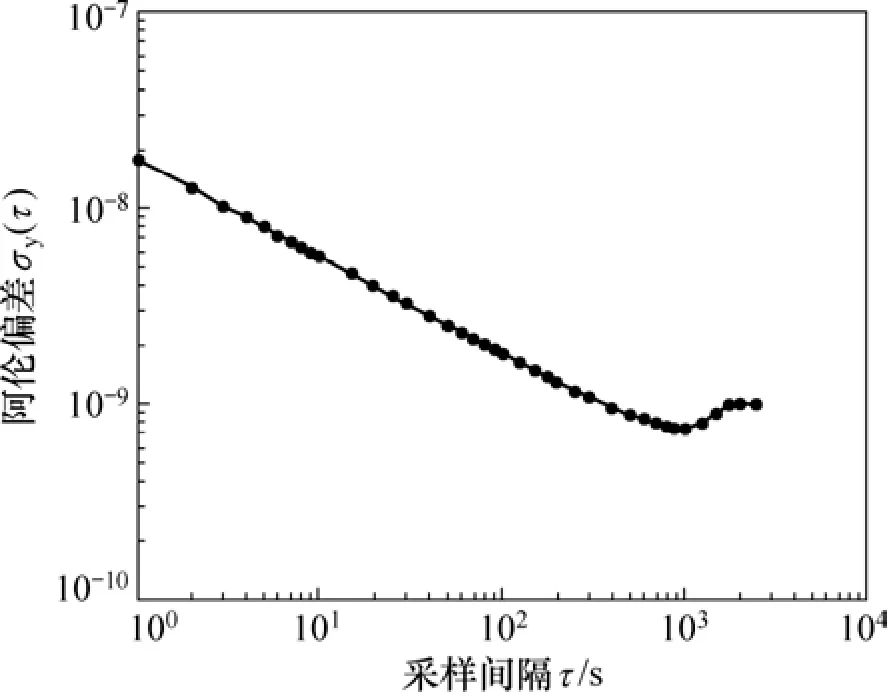
圖2 實驗所用北斗接收機晶振的頻率穩定度Fig. 2 Frequency stability of BDS receiver’oscillator

3.1.2 3-D不完備條件下不連續定位場景

實際測試統計表明，在城市、峽谷等信號遮擋嚴重的區域，3-D不完備條件的平均維持時間約為50 s。因此，從上述連續的歷史觀測數據中分段選擇連續的鐘差解算值，對典型的城市定位場景進行建模，如圖3所示。由圖3可見：整個觀測時段內接收機經歷了3次3-D不完備條件，分別為圖中A，B，C段，其余為完備時段，可以得到鐘差解算值。定義ΔtA，ΔtB和ΔtC的信號中斷時長分別為：ΔtA=54 s，ΔtB=14 s，ΔtC=14 s。

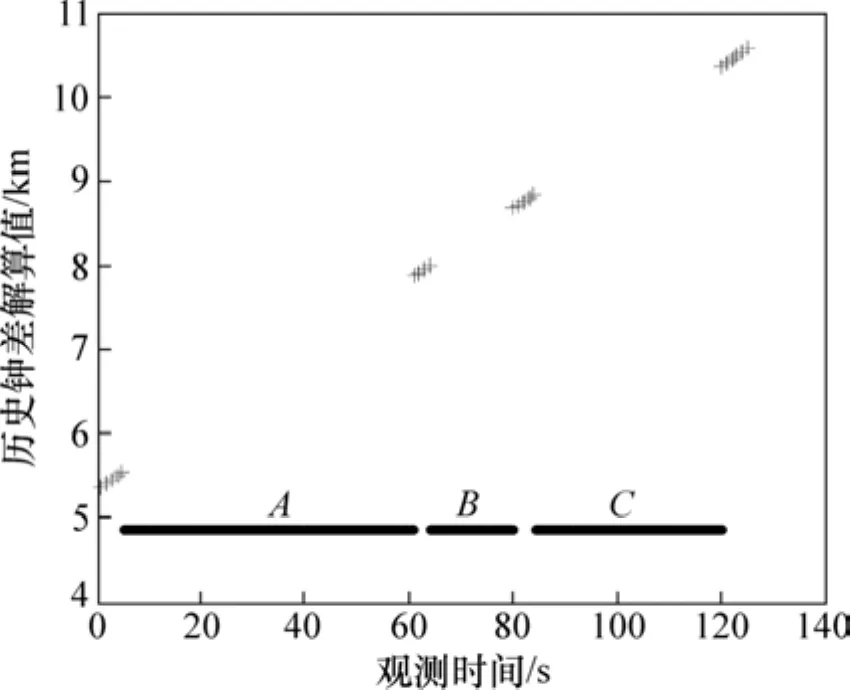
圖3 典型城市環境下的輔助定位場景Fig. 3 Experimental scenario in typical urban environment

3.1.3 3-D不完備條件下組合預測模型性能

(1) 組合預測模型與一般多項式模型比較。2種模型利用上述不等間隔鐘差解算值數據連續外推 155 ～205 s，結果如圖4所示。從圖4可見：隨著預測時間的延長，2種模型的預測誤差都逐漸積累；當預測時為55 s時，組合預測模型的預測誤差達到?0.279 m，一般二次多項式模型達到?0.343 m；當預測時長達到80 s時，組合預測模型的預測誤差達到?1.096 m，一般二次多項式模型達到?1.187 m。而從變化趨勢來講，2種模型是一致的，差異僅表現在預測起點。這是組合預測模型采用加權和廣義延拓逼近優化的結果。總體來看，與一般二次多項式模型相比，組合預測模型預測精度提高1.764 m, 但都能滿足3-D不完備條件下信號中斷時長最大50 s時的精度要求。

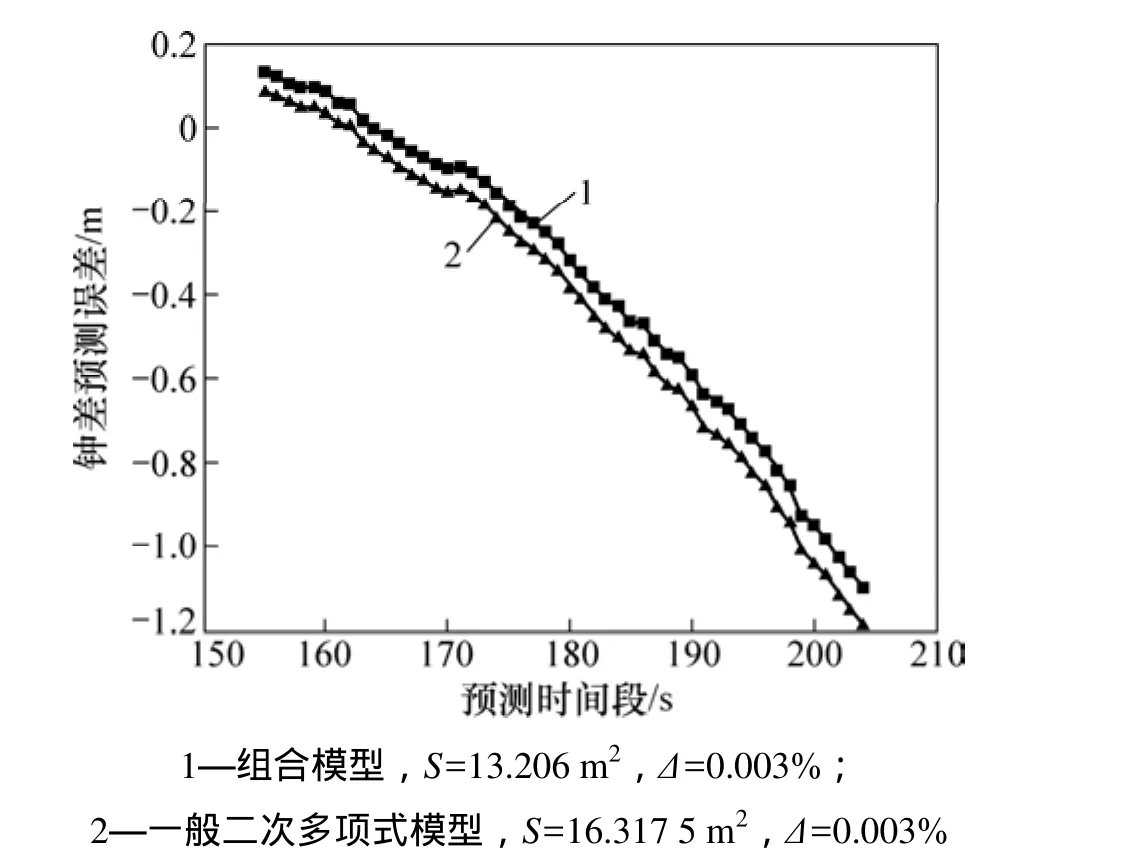
圖4 典型城市環境下組合模型與傳統二次模型鐘差預測結果對比(Δt=30 s)Fig. 4 Comparison of RCB predictions using combination and second-order polynomial model in typical urban environment

(2) 信號遮擋時長對組合預測模型精度的影響。圖5所示為信號受遮擋時長ΔtA，ΔtB，ΔtC不同取值對預測精度的影響。考慮到典型城市環境的特點，各參數的取值范圍滿足式(30)。從圖 5可見：從總的趨勢上講，鐘差預測誤差隨著 Δti的延長而積累，導致定位精度降低。經計算，當ΔtA=23 s時，鐘差預測誤差達到最大值，emax=?2.010 m。

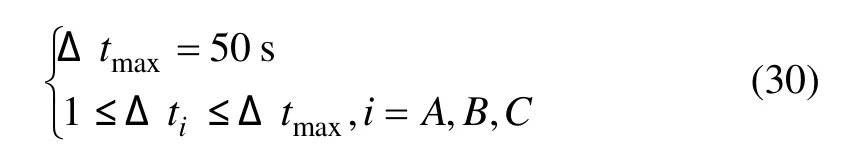
(3) 新息對組合預測模型精度的影響。為了驗證“滑動窗”對預測精度的影響，針對不同的新息類型和滑動方式，采用表1所示的4種方式進行預測精度對比分析，其仿真結果如圖6和圖7所示。

從圖4、圖6、圖7和表1可見：(1) 將鐘差預測值引入模型觀測值序列動態更新模型參數后，將導致模型精度下降；(2) 組合預測模型 2的精度略低于非滑動模型 1。這與滑動窗選取的觀測值長度有關，在觀測數據充足的情況下，可以避免此影響。

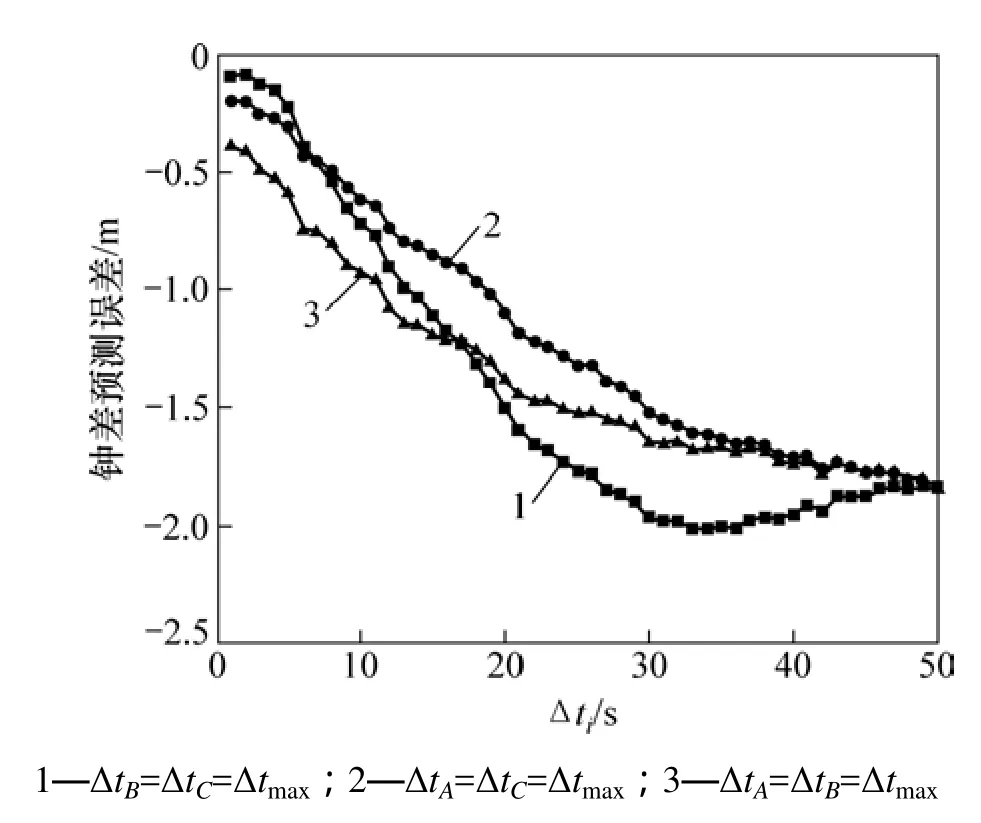
圖5 信號遮擋時長對模型預測精度的影響(i=A，B，C)Fig. 5 Duration of signal blockage effect on prediction accuracy

表1 不同新息對模型預測精度的影響Table 1 Effect of different types of new information on prediction accuracy

圖6 將鐘差解算值作為新息時模型預測精度Fig. 6 Prediction accuracy of models using RCB as new information

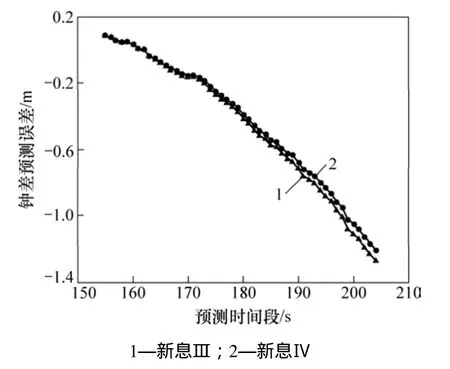
圖7 將健康鐘差預測值作為信息時模型的預測精度Fig. 7 Prediction accuracy of models using predicted RCB as new information

3.2 鐘輔助定位性能評估

為了驗證組合預測模型輔助定位算法的性能，采用受ΔtA，ΔtB和ΔtC等信號受遮擋影響的20個不等間隔歷史鐘差解算值作為歷史觀測數據, 進行輔助定位性能仿真，并與完備條件下的4星定位結果進行比較。其中鐘差輔助定位所用 3顆星為 SV01，SV 04和SV07，完備條件下的定位所用4顆星為SV01，SV 04，SV07和SV08，定位頻率為1 Hz。

圖8和圖9所示為2種定位方法的三維定位誤差及其累積分布。從圖8可見：4星定位的定位誤差為10.960 m；而輔助定位的定位誤差為11.263 m，比正常定位略微增大 2.76%。這是受鐘差預報誤差影響而導致的，但仍然可以滿足短時3-D不完備條件下北斗接收機輔助定位精度需求。

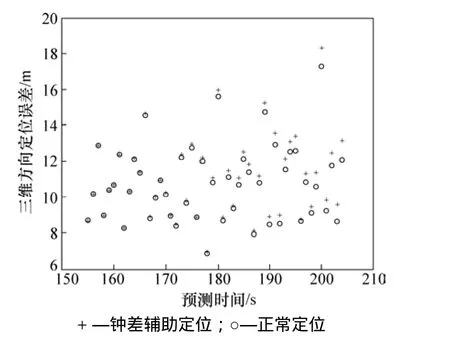
圖8 鐘差輔助定位和四星定位解算結果Fig. 8 Positioning results of clock-aided algorithm and four-satellite method

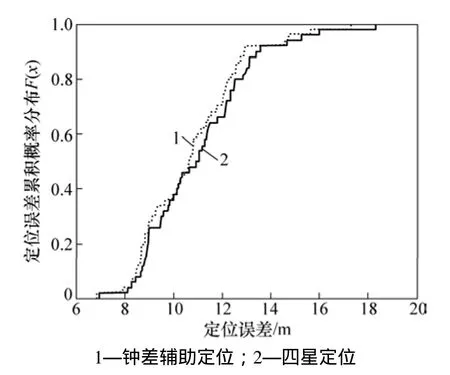
圖9 鐘差輔助定位和四星定位解算結果累積概率分布對比Fig. 9 Cumulative distribution function of positioning errors of clock-aided algorithm and four-satellite method

通過以上的對比分析可以看出：采用預測鐘差解算值進行輔助定位，在短時期內可以繼續為用戶提供與完備條件下性能相當的定位、導航和授時服務，有效地提高了定位的連續性和可用性。

4 結論

(1) 廣義嚴拓逼近法通過優化預測模型在原點的誤差，使得模型具有更高的短期外推精度和可靠性。

(2) 采用“滑動窗”的方式，可以將健康的鐘差解算值引入模型，建立參數動態更新的鐘差預測模型，使模型更好地符合實時變化規律，以保持更高的預測精度。

(3) 線性組合模型通過最優加權組合，實現了單一的改進多項式模型和改進不等間隔灰色模型的優勢互補，有效提高了模型的適用性和可靠性。

(4) 通過北斗接收機的實測數據驗證分析表明，該算法解決了一定外推時間內3-D不完備條件下的定位連續性問題，針對不同類型的不等間隔序列，都能保證滿足導航定位精度要求，有效提高了定位的連續性和可靠性。且該新方法無需增加額外的設備，輔助方式靈活、簡單、經濟。

[1]Misra P N. The role of the clock in a GPS receiver[J]. GPS World, 1996, 7(4): 60?66.

[2]鄭睿, 陳杰. 信號短暫缺失下的不完備條件 GPS定位算法研究[J]. 電子科技大學學報, 2009, 38(4): 496-500.ZHENG Rui, CHEN Jie. New algorithm of GPS positioning in incomplete condition of temporal insufficient signal[J]. Journal of University of Electronic Science and Technology of China,2009, 38(4): 496-500.

[3]陳宇波, 宋迎春. 非高斯噪聲下的車載GPS信號定位算法[J].中南大學學報(自然科學版), 2010, 41(4): 1462?1466.CHEN Yubo, SONG Yingchun. A Bays filter algorithm with non-Gaussian noises based on location of vehicular[J]. Journal of Central South University of Technology (Science and Technology), 2010, 41(4): 1462?1466.

[4]TANG Hui, Kim D. RFID indoor positioning and navigation using a regularized particle filter integrated with a probability model[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division (ION GNSS 2011). Portland:Oregon Convention Center, 2011: 3470-3479.

[5]GUO Yao, WU Wenqi, TANG Kanghua. A new inertial aid method for high dynamic Compass signal tracking based on a nonlinear tracking differentiator[J]. Sensors, 2012, 12(6):7634-7647.

[6]TONG Xiaohua, WU Songchun, WU Shuqing, et al. A novel vehicle navigation map matching algorithm based on fuzzy logic and its application[J]. Journal of Central South University of Technology, 2005, 12(2): 214?219.

[7]TENG Yunlong, SHI Yibing. Clock-based RAIM method and its application in GPS receiver positioning[J]. Journal of Central South University of Technology, 2012, 19(6): 1558?1563.

[8]王永超, 黃智剛. 時鐘改進模型輔助 RAIM 算法研究[J]. 電子學報, 2007, 35(6): 1084?1088.WANG Yongchao, HUANG Zhigang. Research on receiver autonomous integrity monitoring augmented with improved clock bias model[J]. Acta Electronica Sinica, 2007, 35(6):1084?1088.

[9]Bednarz S, Misra P. Receiver clock-based integrity monitoring for GPS precision approaches[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 636-643.

[10]Ramlall R, Streeter J, Schnecker J F. Three satellite navigation in an urban canyon using a chip-scale atomic clock[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division (ION GNSS 2011), Portland: Oregon Convention Center, 2011: 2937-2945.

[11]Kaplan, E D, Hegarty C J. Understanding GPS Principles and Applications[M]. Norwood: Artech House Inc, 2006: 304-305.

[12]SHI Huli, YAN Yihua. Extended interpolation method and its applications in piecewise approximations[C]//Computational and Applied Mathematics, Amsterdam: Elsevier Science Publishers,1992: 229-236.

[13]朱祥維, 肖華, 雍少為, 等. 衛星鐘差預報的 Kalman算法及其性能分析[J]. 宇航學報, 2008, 29(3): 966?970.ZHU Xiangwei, XIAO Hua, YONG Shaowei, et al. The Kalman algorithm used for satellite clock offset prediction and its performance analysis[J]. Journal of Astronautics, 2008, 29(3):966?970.