有序堆積填充床傳熱傳質與反應耦合的數值研究

杜娟，魏小蘭，丁靜，陸建峰，秦貫豐，楊敏林，楊曉西,

(1. 華南理工大學 傳熱強化與過程節能教育部重點實驗室，廣東 廣州，510640；2. 中山大學 工學院，廣東 廣州，510006；3. 東莞理工學院 廣東省分布式能源系統重點實驗室，廣東 東莞，523808)

催化劑能夠大幅度提高原料利用率及反應效率，一直被廣泛應用于化工等領域，而接觸式催化反應的場所一般采用填充床的形式。填充床分為有序堆積和隨機堆積2種方式。采用有序堆積方式的填充床能夠提高填充床內空間利用率，進而提高催化劑的使用效率，因此具有非常廣闊的應用前景[1]。由于物料在填充床的流場、溫度場及組分分布等的復雜性，實驗研究僅能獲得如床層壓降、原料轉化率與收率等宏觀信息，缺乏對填充床床層內部流場及組分分布等微觀信息的描述。計算流體力學(computational fluid dynamics，CFD)研究能彌補實驗研究的弊端，將數值模擬與實驗研究相結合，可以在實驗基礎上對填充床反應器進一步優化與設計，大大縮短了研究時間，同時也能對實驗過程中難以實現的反應條件進行研究，并獲得流場及組分分布等細節信息。填充床內顆粒不同堆積方式是導致流動及傳遞差異的主要原因。Calis等[1]構建了壓降較小的有序堆積填充床模型，以整個床層為研究對象，分析了在不同N時(1≤N≤2)流體運動及流場分布情況，發現模擬值與實驗值的平均相對誤差為10%左右，模擬的局部流場與激光多普勒測速法測出的實驗局部流場吻合較好。Romkes等[2]在此基礎上進一步研究了該有序堆積填充床床層模型的傳熱特性，模擬值與實驗值的平均相對誤差不超過15%，為工業填充床的仿真設計提供了數值建模基礎。Nijemeisland等[3]設計了N=4球形催化劑顆粒的三維模型，研究了填充床內部速度場、渦流場與壁面熱流密度分布，發現周期性的流動模型與整個填充床床層模型的流動特性相似。Jafari等[4]研究填充床內隨機堆積對流場分布的影響時將整個管內床層作為整體處理，考察了雷諾數對無量綱壓降的影響。Guardo等[5]研究了空間填充率最大情況下 44個顆粒按照無序排列時的流體的流動及傳熱性質，考察了雷諾數對不同湍流模型下填充床的壓降與傳熱特性的影響。Gunjal等[6]研究了不同堆積方式如簡單立方堆積(ε=0.476 4，ε為孔隙率)，斜方堆積(ε=0.259 5)與面心立方堆積(ε=0.302)等對速度場分布、傳熱與阻力特性的影響。Kim 等[7]考察了催化劑顆粒在簡單立方(ε=0.489)、體心立方(ε=0.337)及面心立方(ε=0.278)排列方式下流體在填充床的流場與溫度分布特性，發現壓降隨著孔隙率的降低而增加，體心立方的傳熱速率最高。可見：不同堆積方式對填充床床層內的流動、傳熱及流場分布等有著重要的作用，并直接影響催化劑的催化效率與泵功耗。填充床內催化劑顆粒的堆積方式也決定著反應發生的程度。不論是有序堆積還是隨機堆積，模型構建對數值模擬結果的準確性具有重大影響[1?2,4]。在大多數文獻中[1?2,8?9]，管內流體的物性多采用常物性，忽略了溫度等對物性參數的影響；且研究過程沒有考察化學反應的發生，因此不能說明發生反應后管內熱質傳遞規律。另外，模型構建需要以反應動力學為基礎，而化學反應過程非常復雜，因而涉及化學反應的數值模擬僅局限于少數幾個反應體系，如甲烷燃燒[10?12]，三氧化硫分解[13?14]等。CO2/CH4重整反應是典型的強吸熱化學反應，能應用于高溫熱化學儲能過程[15?17]；該體系能利用溫室氣體CO2，是緩解溫室效應的有效途徑。因此，研究CO2/CH4重整反應在填充床床層內的熱質傳遞及反應特性對節能減排有非常重要的作用。在此，本文作者基于堆積方式對填充床床層內流場等分布情況的影響，構建了一類新型的有序堆積方式，用于研究管內發生CO2/CH4重整反應情況下的填充床內部的流動、傳熱及反應特性。構建了N=1.67，2，2.16的3種催化劑堆積模型，分析了填充床床層在耦合CO2/CH4重整反應的情況下管內流體的流動、傳熱及組分分布特性，并考察了有無耦合反應對管內流動、傳熱及組分分布情況的影響。

1 CFD模型及數值方法

1.1 模型建立

為了研究填充床堆積方式對床層流動、傳熱與反應的影響，考察了3種堆積情況，假設催化劑顆粒為規則球形。

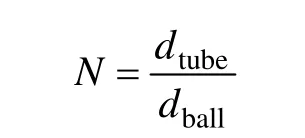
式中：dtube為管徑；dball為催化劑顆粒直徑。

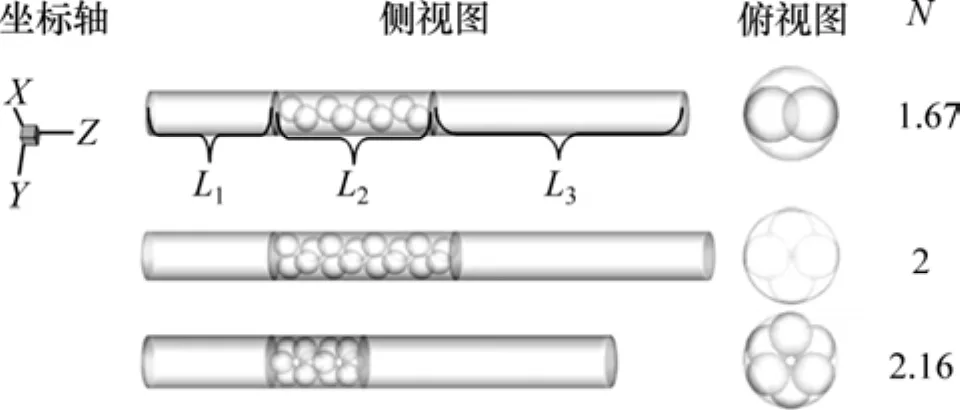
圖1 不同堆積方式結構示意圖Fig. 1 Geometric scheme for different stack structures

根據N將堆積方式分為3種，如圖1所示，分別為N=1.67，N=2和N=2.16。其中，N=1.67時，每一層的球與管壁相切且與下一層的球相切；N=2時，每一層的2個球相切，2個球之間夾角為180°，同時2個球分別與管壁相切，且與下一層的2個球呈錯列方式；N=2.16時，每一層的3個球相切且夾角為120°，并與下一層的3個球呈錯列方式。每1種堆積方式的填充床管直徑dtube=20 mm。不同堆積方式的具體結構參數見表1。

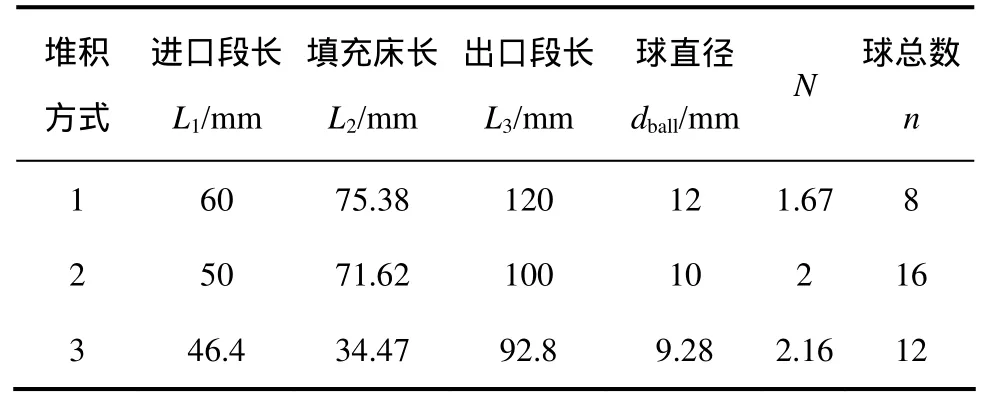
表1 不同堆積方式結構參數Table 1 Geometric parameters for different stack structures

1.2 控制方程

模擬時做如下假定：(1) 管內流動為三維、穩態、不可壓縮層流流動，滿足質量、動量、能量與組分守恒方程，化學反應模型采用層流有限速率法；(2) 催化劑顆粒為有序堆積，顆粒粒徑相同；(3) 催化劑顆粒為絕熱邊界，無內熱源；(4) 不考慮重力影響及黏性耗散；(5) 不考慮輻射換熱、壓力變化做功等。質量、動量、能量與組分守恒方程分別如式(1)，(2)，(3)和(4)所示，其中，Ri為第i組分在化學反應中的凈生成速率；Di,m為混合物中第i組分的擴散系數。模型中采用層流有限速率法計算化學反應，Ri根據阿倫尼烏斯公式計算。

連續性方程：

動量方程：

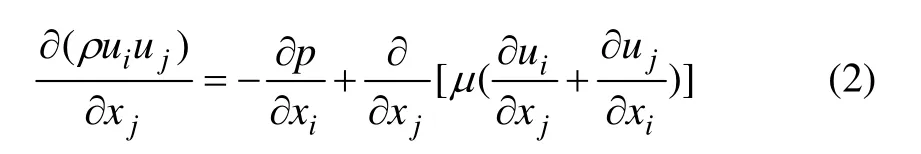
能量方程：

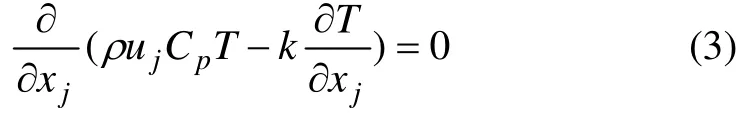
組分方程：

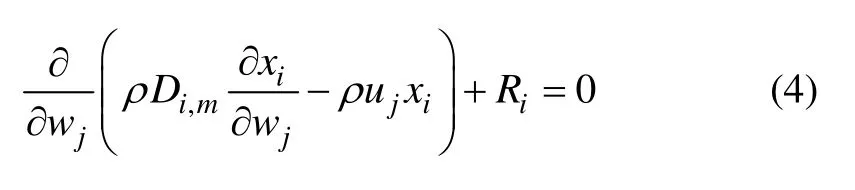
1.3 網格劃分

網格劃分采用Gambit 2.2.30軟件劃分，圖2所示為局部網格劃分示意圖(以N=2為例)，如圖2所示，進口段跟出口段采用六面體網格，催化劑床層段采用四面體網格，對管壁與催化劑表面進行網格加密。當球與管壁相切及球與球相切時，直接進行網格劃分，由于存在尖銳的縫隙及曲面，網格質量很差，甚至難以劃分出來，因此為了保證較好的網格質量，對球的直徑進行了一定比率的縮小[1]。為了保證網格獨立性，圖3所示為努賽爾數隨網格數的變化關系，如圖3所示，當網格數量達到1 291 010后，該網格數努賽爾數與1 685 181網格數努賽爾數的偏差為1.04 %，可認為達到網格獨立性，因此在本文計算中，采用網格數為1 291 010進行計算。

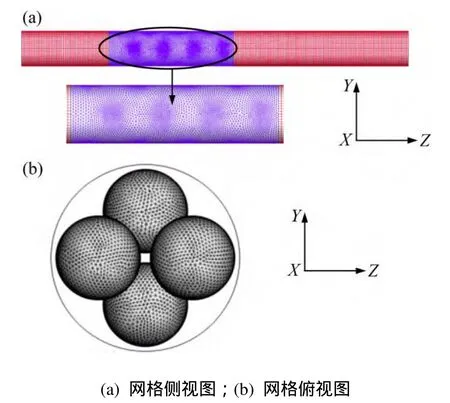
圖2 局部網格劃分示意圖Fig. 2 Schematic of local grid generation

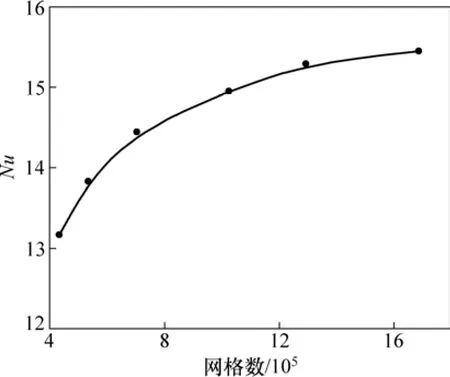
圖3 N=2的網格獨立性Fig. 3 Grid independence for N=2

1.4 數值方法與邊界條件

數值模擬采用Fluent 6.3.26軟件進行計算。計算采用三維壓力基雙精度求解器求解，速度與壓力耦合采用SIMPLE算法，壓力離散為Standard格式，對流擴散項均采用二階迎風格式離散。圖4所示為模型的邊界條件。進出口分別采用速度進口與壓力出口，進料氣為CH4與CO2，按摩爾比1:1進料，采用氦氣作為稀釋氣(氦氣在模型中不參與反應)。反應過程中采用Pt-Ru/γ-Al2O3作為催化劑，活化能Ea=33.7 kJ/mol，指前因子A=2 052 883 m3·kmol?1·s?1。氣體混合物的密度符合不可壓縮理想氣體定律，質量擴散采用動力學理論，對每個單獨組分采用多項式擬合來考慮溫度對比熱容的影響。為了減少進出口效應，進出口分別延長5倍與10倍催化劑顆粒直徑長度。忽略管壁厚度并采用恒壁溫(Tw=1 073 K)。為了保證收斂，整個計算區域各控制方程的殘差控制在10?6以下。

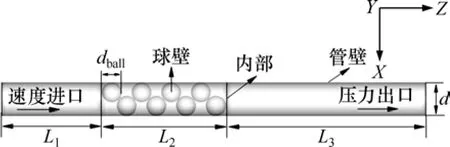
圖4 邊界條件示意圖Fig. 4 Schematic for boundary conditions

1.5 模型驗證

為了驗證填充床堆積模型的合理性，基于填充床單球模型進行模型驗證，經驗公式采用單球模型傳熱關系式[18?19]。在一個近似無限大的空間內，考察了dball=10 mm單球的傳熱特性，用于驗證物理模型的準確性。為了消除進出口效應及壁面效應，進口段與出口段分別為L1=10dball，L2=20dball，球中心與管壁的距離為d=10dball。單球模型示意圖見圖5(a)。

其中，Ranz 和Marshall關系式如下

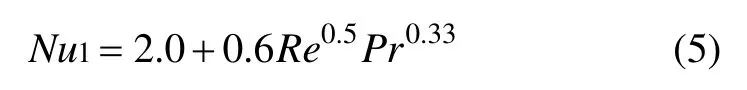
Whitaker關系式如下

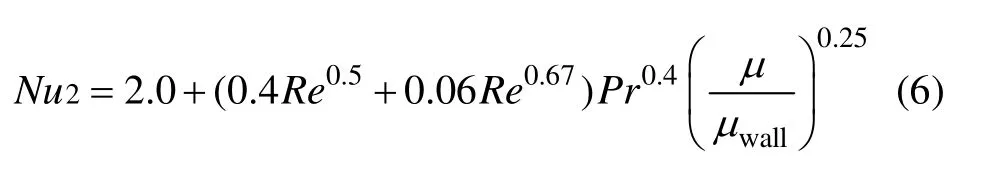
圖5(b)所示為單球模型模擬值與經驗值的對比關系。從圖5可以發現：模擬值變化趨勢與經驗值變化趨勢吻合良好，模擬值與經驗值的相對平均偏差不超過 8.05%。因此，可認為本文所采用模型及數值方法是可靠的。

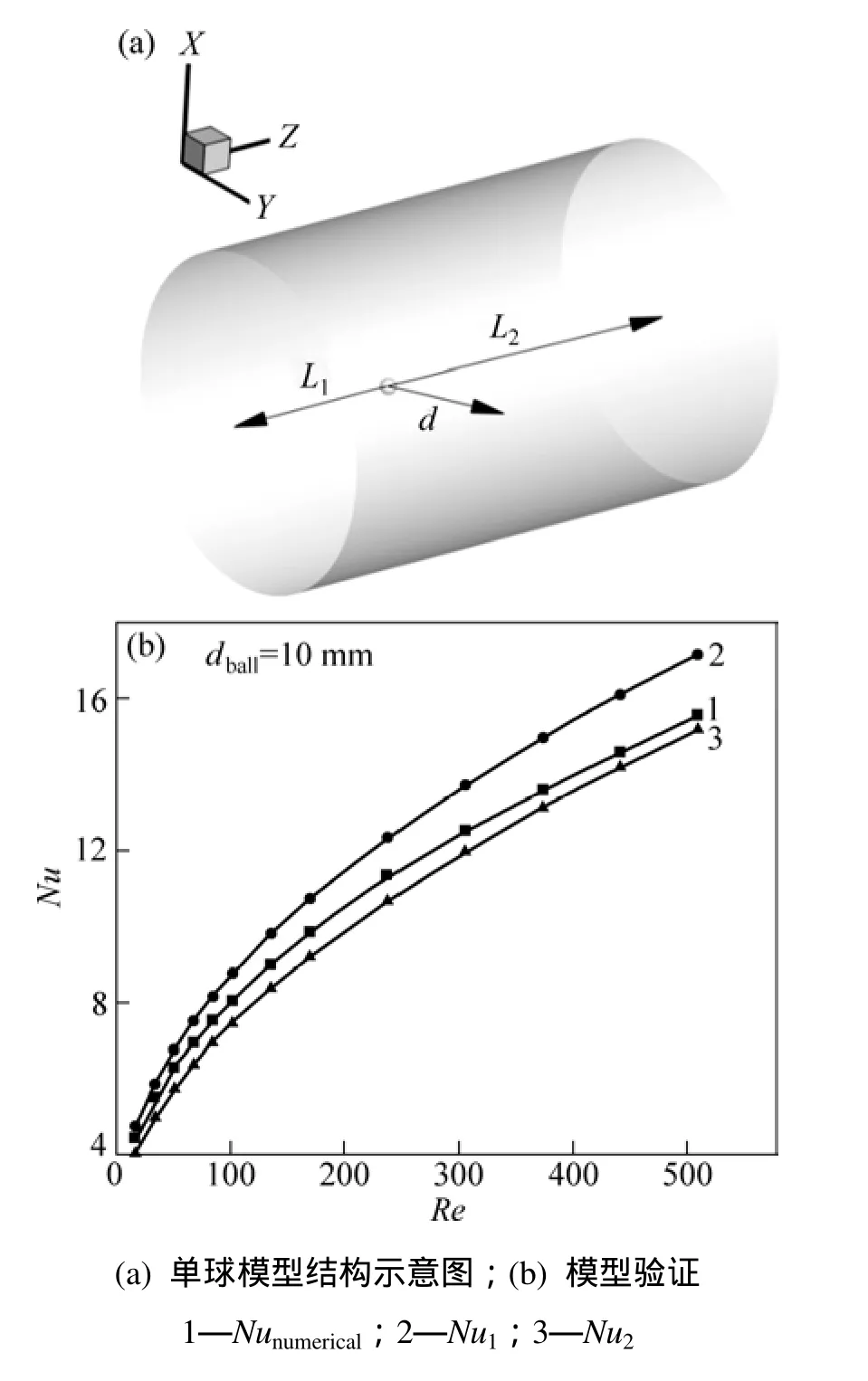
圖5 單球模型結構示意圖及模型驗證Fig. 5 Schematic of single ball model and model verification

2 無反應時不同堆積方式對平均傳熱與流動特性的影響

圖6所示為不同堆積方式下壓力梯度(ΔP/L2)與阻力系數(f)隨雷諾數(Re)的變化關系。由圖 6可知：3種堆積方式的壓力梯度均隨著雷諾數的增加而增加，阻力系數則隨雷諾數增加而減小；隨N的增加，阻力系數越來越大。以u=0.5 m/s時N=1.67堆積方式為例，催化劑床層內催化劑顆粒所占的總阻力為75%，而床層管壁總阻力占25%，因此，催化劑顆粒的阻力特性對催化劑床層的阻力特性分布起關鍵性作用。

圖7所示為不同堆積方式下催化劑顆粒形體阻力比率與摩擦阻力比率隨流速的變化關系。總體上，催化劑顆粒形體阻力占總阻力的比例為71%～77%，而顆粒摩擦阻力占23%～29%，因此形體阻力在催化劑顆粒阻力特性分布中起關鍵性作用。隨著流速增加，催化劑顆粒下游產生的回流增強，因此形體阻力比率增加。此外，催化劑顆粒越密集，流動分離與回流越多，因此同流速下，N=2.16的形體阻力比率較N=1.67與2時的大。

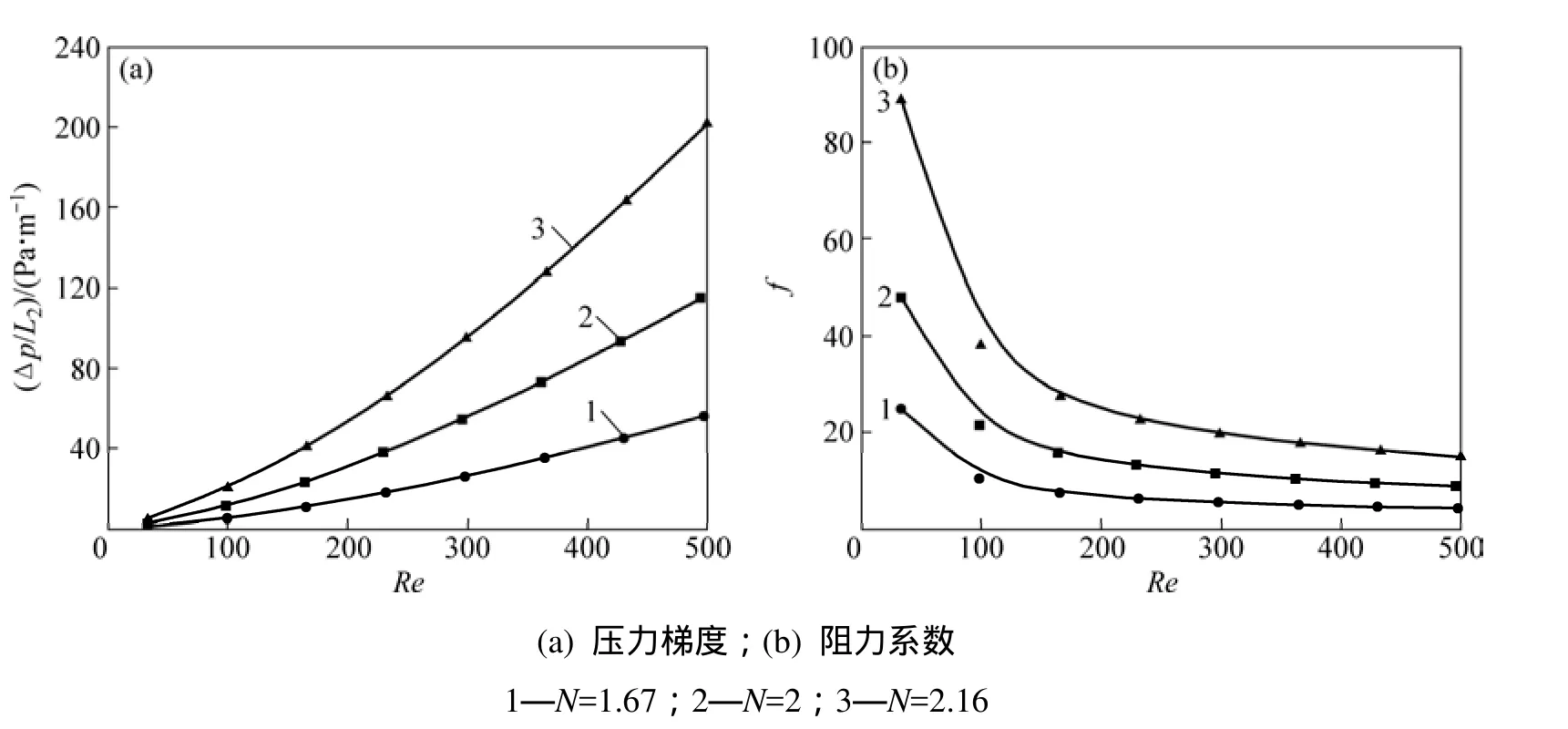
圖6 不同堆積方式下壓力梯度與阻力系數隨雷諾數的變化Fig. 6 Variations of ΔP/L and f with Re for different stack structures

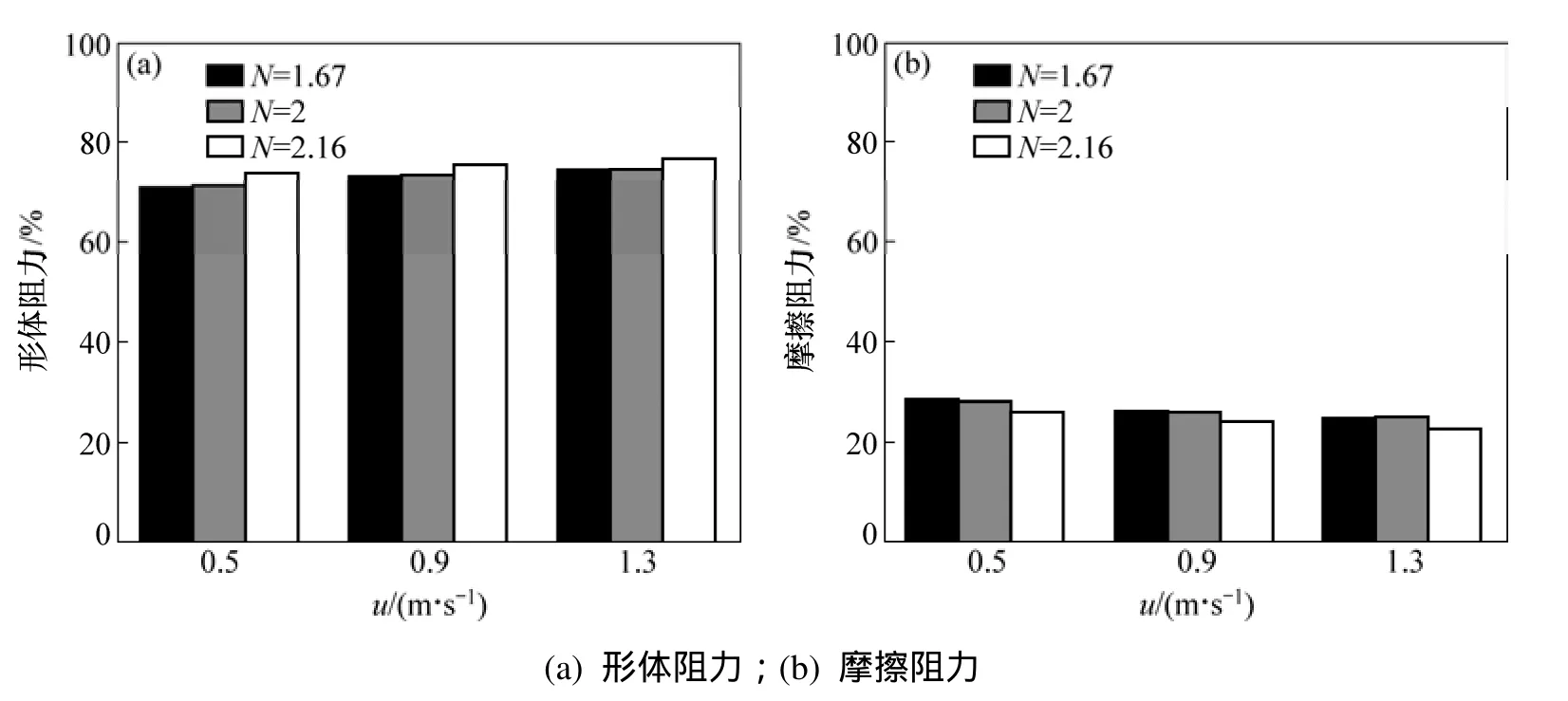
圖7 不同堆積方式下形體與摩擦阻力的對比Fig. 7 Comparisons of different drag for different stack structures

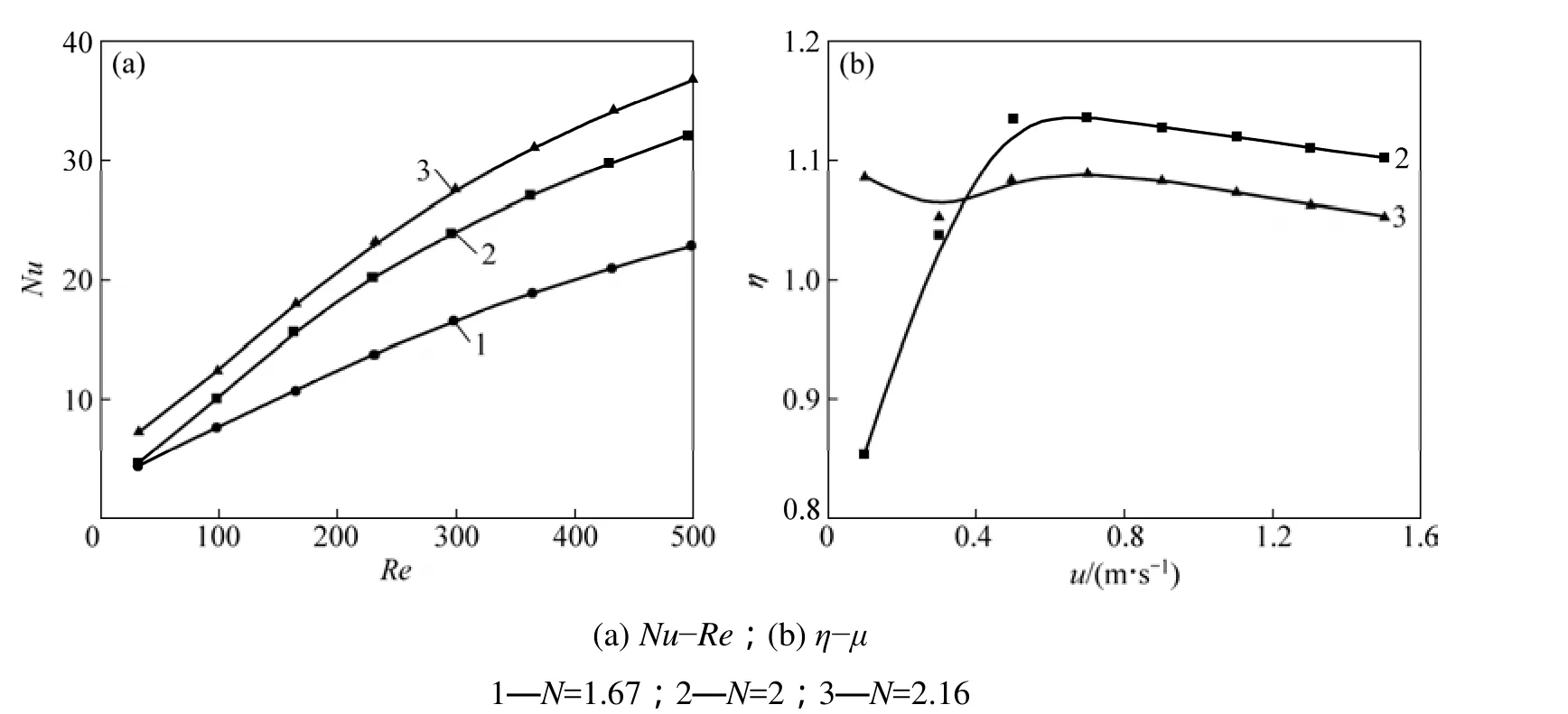
圖8 不同堆積方式下努賽爾數與傳熱因子隨雷諾數的變化Fig. 8 Variations of Nu and η with Re for different stack structures

圖8 所示為努塞爾數(Nu)與傳熱綜合因子(η)隨雷諾數(Re)的變化關系。其中，傳熱綜合因子用η來表示，，其中，η代表同功耗下的傳熱增幅，Nu與f分別代表其他2種堆積方式的努賽爾數與阻力系數，NuN=1.67與fN=1.67分別代表N=1.67堆積方式的努賽爾數與阻力系數。由圖8可知，努塞爾數都隨雷諾數的增加而增加，這表明提高流速有利于傳熱速率的提高。另外，在同流速下，隨著N的增加，即同層顆粒數的增多，傳熱速率依次提高，這是因為當顆粒數量增多時，孔隙率越來越小，顆粒對流體的擾動越來越強烈，加劇了管內流體的混合，從而提高了傳熱速率。由圖8(b)可知：在低流速下，N=2的傳熱因子低于 1，這說明此時的傳熱綜合性能不及N=1.67堆積方式，即傳熱速率的提高，功耗增加太多。在流速大于0.3 m/s后，N=2的傳熱因子較N=2.16的大，這說明3種堆積方式中，在大部分流速范圍內，N=2堆積的傳熱綜合因子最佳。

3 耦合反應時堆積方式對 CO2/CH4反應的影響

在研究沒有耦合反應時傳熱與流動特性的基礎上，進一步考慮了耦合CO2/CH4反應后管內的熱質傳遞規律。圖9所示為以N=1.67時無反應與有反應時速度云圖場與溫度云圖場的對比情況。由圖9可見，在反應氣沿軸向流過一定數量催化劑顆粒后，呈現出周期性流動的特征，達到周期性后，有反應時的局部流速較無反應時的大。另外，耦合反應后，與無反應時相比，由于CO2/CH4反應是強吸熱反應，催化劑表面出現了明顯的溫度降，而且床層內溫升幅度相對較小。圖10所示為N對催化劑表面平均溫度的影響。無論有無耦合反應，催化劑顆粒表面溫度都是隨著流速的增加而降低，這是因為流速越大，流體在填充床層內的停留時間越短，流體從管壁獲得的熱量相應減少，同時傳遞給顆粒表面的熱量也相應減少，導致顆粒溫度降低。在同流速下，N=2的顆粒表面溫度比其他兩者要高，這是因為在同流速下，N=2的局部流速相對于其他2種堆積方式的流速要小(圖11所示)，從而流體與顆粒接觸時間相應要長，傳遞給顆粒的熱量也增加。另外，N=1.67的表面溫度較N=2.16的要高一些，這是因為N=1.67堆積方式的表面積為0.002 927 198 m2，而N=2.16堆積方式的表面積為0.002 626 218 m2，N=1.67的表面積相對較大，所以吸收熱量較多，因此溫度相應較高。對比圖 10(a)與圖 10(b)可以發現，耦合反應后，催化劑顆粒表面的溫度較低，這是因為甲烷重整二氧化碳反應是一個強吸熱反應，同時耦合反應后，局部流速增加導致停留時間變短(圖11所示)，從而導致催化劑顆粒表面上的溫度降低。

圖9 N=1.67無反應與耦合反應時X=0 mm截面上的速度場與溫度場云圖(u=0.9 m/s)Fig. 9 Contours of velocity and temperature for N=1.67 without or with reaction on X=0 mm plane at u=0.9 m/s

圖 12所示為不同堆積方式對催化劑表面甲烷轉化率的影響。由于本文所采用的堆積方式中，顆粒數、直徑與堆積方式都不同，因此不能簡單地比較催化劑床層的進出口甲烷摩爾分數，為便于比較，采用單位面積催化劑甲烷轉化率來定量描述催化劑堆積方式對甲烷轉化率的影響，此處單位面積催化劑甲烷轉化率定義為：ε=(xinlet?xoutlet)/(xinlet×Sball)，其中，xinlet和xoutlet分別為進出口處CH4摩爾分數；Sball為顆粒的表面積。由圖12可知，不同堆積方式對轉化率的影響與對顆粒表面溫度的影響趨勢剛好相反，這是因為甲烷重整二氧化碳反應是一個吸熱反應，球表面上甲烷的轉化率越高，球表面溫度也就越低。由于單位面積催化劑甲烷轉化率受催化劑顆粒表面積、顆粒布局與局部流速的綜合影響，N=2.16堆積方式的甲烷轉化效率最高，其次是N=1.67，再次是N=2，后兩者相差不是很大。另外，隨著流速增加，轉化率降低，這是由于流速增加導致反應氣與催化劑接觸的停留時間變短，在催化劑顆粒表面上產生反應轉化的原料量也越小，從而導致轉化率相應要低一些。在研究范圍內，N=2.16具有最佳的催化效率。

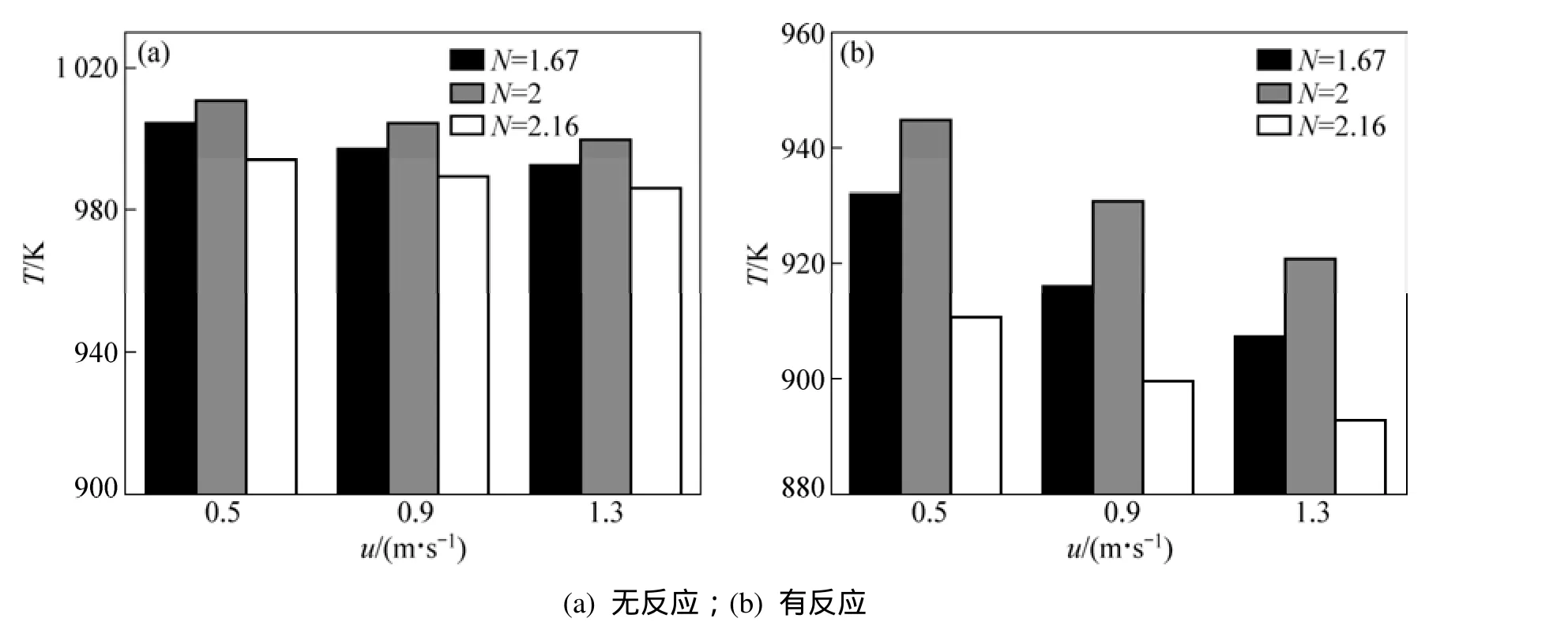
圖10 不同堆積方式對催化劑表面溫度的影響Fig. 10 Effect of different stack structures on surface temperature of catalysts

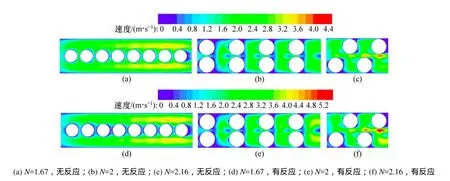
圖11 不同堆積方式X=0 mm截面的速度分布云圖(u=0.9 m/s)Fig. 11 Contours of velocity for different stacked structures on X=0 mm plane at u=0.9 m/s

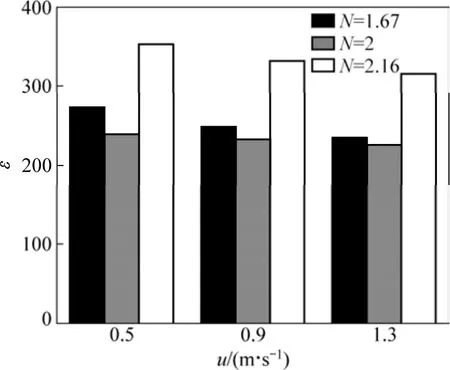
圖12 不同堆積方式對催化劑比表面甲烷轉化率的影響Fig. 12 Effect of different stack structures on CH4 conversion per surface area of catalysts

圖13 所示為N=1.67時，填充床X=0 mm截面上的甲烷、二氧化碳、一氧化碳和氫氣摩爾分數分布圖。由圖13可見，在催化劑表面附近，甲烷與二氧化碳的摩爾分數急劇降低；而一氧化碳與氫氣的摩爾分數在催化劑表面附近明顯增加，這表明了在催化劑表面發生了化學反應。另外，甲烷與二氧化碳的摩爾分數在管內軸向流動方向逐漸降低，而一氧化碳與氫氣的摩爾分數則隨著軸向流動方向逐漸升高。這是因為反應氣沿軸向被逐漸加熱，溫度相應升高，而CO2/CH4反應速率是溫度的正函數，因此溫度越高，催化劑表面甲烷反應的量也就越多。

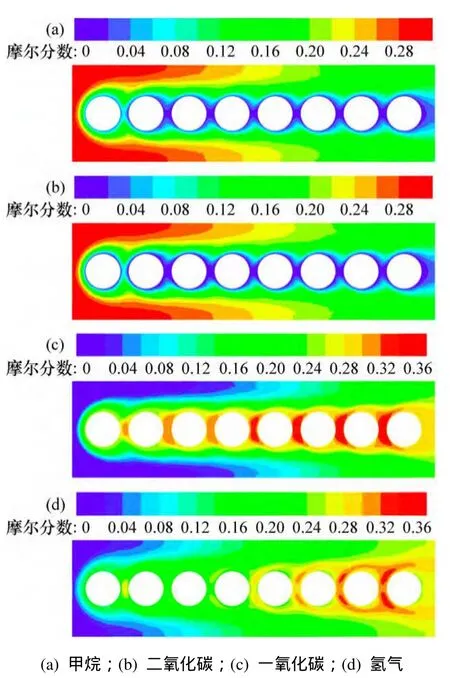
圖13 N=1.67堆積方式在X=0 mm截面的摩爾分數云圖(u=0.9 m/s)Fig. 13 Different contours of stack structure forN=1.67 on X=0 mm plane at u=0.9 m/s

4 結論

(1) 沒有耦合反應時，填充床的阻力與傳熱速率都隨N的增加而增加，N=2.16時，傳熱速率最高，同時阻力系數也最高，填充床內的阻力特性主要受催化劑顆粒的形體阻力支配，在大多數雷諾數范圍內，N=2時傳熱綜合性能更高。另外，隨著流速的增加，停留時間的減少，催化劑表面溫度降低。由于局部流速較低，N=2時表面溫度最高，其次是N=1.67，最低是N=2.16。

(2) 耦合反應后，由于 CO2/CH4是強吸熱反應，催化劑表面的溫度都比無反應時的溫度低，但操作流速跟堆積方式對溫度的影響與無反應時相同。不同N對催化劑表面單位面積轉化率有重要影響，受催化劑顆粒表面積、顆粒布局與局部流速的綜合影響，N=2.16時轉化率最高，其次是N=1.67，最后是N=2。從N=1.67的摩爾分數云圖可以發現，CO2/CH4在催化劑表面發生了化學反應，且沿軸向隨著溫度的升高，反應加劇，CO2/CH4轉化率提高。

[1]Calis H P A, Nijenhuis J, Paikert B C, et al. CFD modeling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing[J]. Chemical Engineering Science, 2001, 56(4): 1713?1720.

[2]Romkes S J P, Dautzenberg F M, Bleek C M, et al. CFD modeling and experimental validation of particle-to-fluid mass and heat transfer in a packed bed at very low channel to particle diameter ratio[J]. Chemical Engineering Journal, 2003, 96(1/3):3?13.

[3]Nijemeisland M, Dixon A G. CFD study of fluid flow and wall heat transfer in a fixed bed of spheres[J]. American Institute of Chemical Engineers, 2004, 50(5): 906?921.

[4]Jafari A, Zamankhan P, Mousavi S M, et al. Modeling and CFD simulation of flow behavior and dispersivity through randomly packed bed reactors[J]. Chemical Engineering Journal, 2008,144(3): 476?482.

[5]Guardo A, Coussirat M, Angels Larrayoz M, et al. CFD flow and heat transfer in nonregular packings for fixed bed equipment design[J]. Industrial and Engineering Chemistry Research, 2004,43(22): 7049?7056.

[6]Gunjal P R, Ranade V V, Chaudhari R V. Computational study of a single-phase flow in packed beds of spheres[J]. American Institute of Chemical Engineers, 2005, 51(2): 365?378.

[7]Kim M H, Lim H S, Lee W J. Computational fluid dynamics assessment of the local hot core temperature in a pebble-bed type very high temperature reactor[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(1): 012905.1?012905.6.

[8]趙巖, 王亮, 陳海生, 等. 填充床顯熱及相變儲熱特性分析[J].工程熱物理學報, 2012, 33(12): 2052?2057.ZHAO Yan, WANG Liang, CHEN Haisheng, et al. Analysis on thermal storage characteristic of sensible and latent heat in packed beds[J]. Journal of Engineering Thermophysics, 2012,33(12): 2052?2057.

[9]梅紅, 李成岳, 劉輝, 等. 結構化金屬填充床傳遞特性的數值模擬[J]. 化工學報, 2005, 56(7): 1175?1180.MEI Hong, LI Chengyue, LIU Hui, et al. Simulation of heat transfer and pressure drop of metal structured packed bed[J].Journal of Chemical Industry and Engineering (China), 2005,56(7): 1175?1180.

[10]Wang J H, Huang Z H, Tang C L, et al. Numerical study of the effect of hydrogen addition on methane-air mixtures combustion[J]. International Journal of Hydrogen Energy, 2009,34(2): 1084?1096.

[11]鐘北京, 洪澤愷. 微燃燒器內甲烷催化燃燒的數值模擬[J].熱能動力工程, 2003, 18(6): 584?588.ZHONG Beijing, HONG Zekai. Numerical simulation of catalytic combustion of CH4in a microburner[J]. Journal of Engineering for Thermal Energy and Power (China), 2003, 18(6):584?588.

[12]凌忠錢, 周昊, 錢欣平, 等. 自由堆積多孔介質內預混燃燒火焰傳播[J]. 化工學報, 2008, 59(2): 722?725.LING Zhongqian, ZHOU Hao, QIAN Xinping, et al.Propagation of premixed combustion wave of methane/air in packed bed[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(2): 722?725.

[13]Kuchi G, Ponyavin V, Chen Y T, et al. Numerical modeling of high-temperature shell-and-tube heat exchanger and chemical decomposer for hydrogen production[J]．International Journal of Hydrogen Energy, 2008, 33(20): 5460?5468.

[14]Nagarajan V, Ponyavin V, Chen Y T, et al. Numerical study of sulfur trioxide decomposition in bayonet type heat exchanger and chemical decomposer with porous media zone and different packed bed designs[J]. International Journal of Hydrogen Energy,2008, 33(22): 6445?6455.

[15]Steinfeld A, Kirillov V, Kuvshinov G, et al. Production of filamentous carbon and hydrogen by solar thermal catalytic cracking of methane[J]. Chemical Engineering Science, 1997,52(20): 3599?3603.

[16]W?rner A, Tamme R. CO2reforming of methane in a solar driven volumetric receiver-reactor[J]. Catalysis Today, 1998,46(2/3): 165?174.

[17]Du J, Yang X X, Ding J, et al. Carbon dioxide reforming of methane over bimetallic catalysts of Pt-Ru/γ-Al2O3for thermochemical energy storage[J]. Journal of central south University, 2013, 20(5): 1307?1313.

[18]Ranz W E, Marshall W R. Evaporation from drops[J]. Chemical Engineering Progress, 1952, 48(1): 141?146.

[19]Whitaker S．Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles[J]. American Institute of Chemical Engineers, 1972, 18(2): 361?371.

[20]Webb R L, Eckert E R G. Application of rough surfaces to heat exchanger design[J]. International Journal of Heat and Mass Transfer, 1972, 15(9): 1647?1658.