基于雙二次插值的2.5維FCSEM有限元正演模擬

柳建新 ，湯文武 ，童孝忠

(1. 中南大學 地球科學與信息物理學院，湖南 長沙，410083；2. 有色資源與地質災害探查湖南省重點實驗室，湖南 長沙，410083)

2.5 維數值模擬指的是源為三維的、正演模型為二維的地球物理數值模擬問題[1?3]。眾所周知，2.5維數值模擬問題有著重要的實用價值，這是因為將三維問題簡化為2.5維模型后只需要對剖面而不是整個體積空間進行離散處理，這樣就大大減小了矩陣的尺寸[4]。

2.5維頻率域可控源電磁法(frequency domain controlled-source electromagnetic, FCSEM)的有限元正演模擬，國內外都進行了研究。Unsworth等[5]將一次場與二次場分離，利用有限元對二維地電模型下水平電偶源的電磁場響應進行了模擬計算；Mitsuhata[6]借鑒地震模擬中的偽delta函數模擬電偶源，只需一次性計算總場，并利用等參有限元實現了帶地形的2.5維頻率域電磁正演模擬；底青云等[7?8]對2.5維頻率域電磁進行了有限元模擬并給出了一組波數，對層狀模型的模擬計算效果較好；薛東川等[9?10]對2.5維頻率域電磁的吸收邊界條件進行了討論，發現吸收邊界條件能夠有效壓制邊界處的反射。在此，本文作者在前人研究基礎上，重點研究基于雙二次插值的FCSEM有限元正演模擬，并對波數選取進行研究，給出一組兼顧計算速度及模擬精度的波數。

1 有限元方程的推導

圖1所示為2.5維FCSEM正演模擬示意圖：其y方向為走向方向，水平電偶源Idy沿走向方向布置。電磁法勘探是基于電磁場理論的一類地球物理勘探方法，2.5維頻率域可控源電磁(FCSEM)也應滿足麥克斯韋方程。假設時諧因子為eiωt，則麥克斯韋方程表示如下[3]：

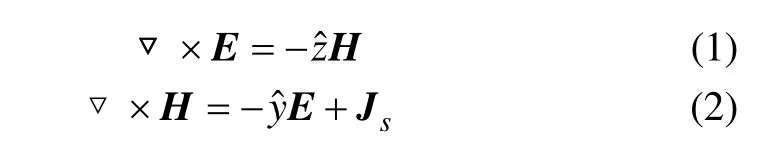
式中：E為電場強度；H為磁場強度；Js為外加電偶源；阻抗率=iμω；導納率=σ+εω。對式(1)和(2)中的所有電場分量及磁場分量都進行傅里葉變換得：

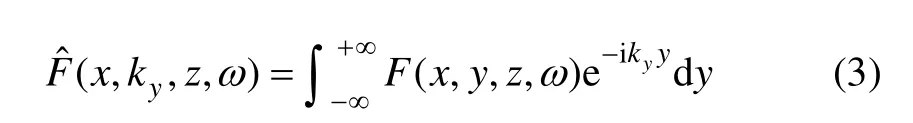
可以得到如下的微分控制方程[6]：

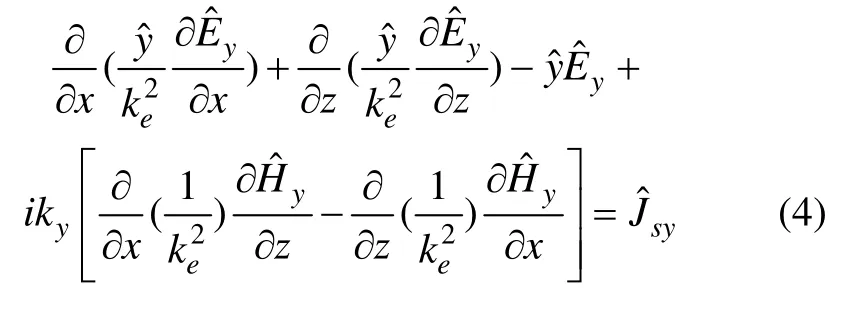
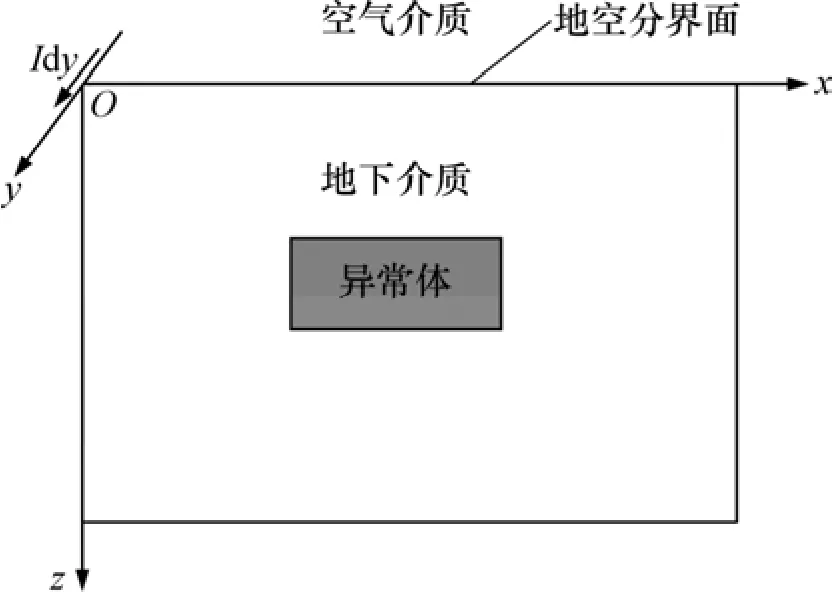
圖1 2.5-D FCSEM模擬示意圖Fig. 1 Simulation schematic diagram of 2.5-D FCSEM

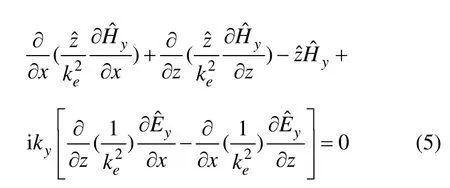
首先利用有限元方法求解式(4)和(5)可得到傅氏域中的電場分量y及磁場分量y，再利用式(6)～(9)求得其余4個分量，最后通過傅氏逆變換可求得真實電磁場。這里直接給出由伽遼金有限元方法推導得到的有限元方程如下[6]：

2 有限元求解過程

先對模擬區域進行剖分。由于同等計算量下雙二次插值一般較雙線性插值精度高，因此，本文采用雙二次插值以提高計算精度；接著對各個單元進行分析、計算，得到各個小型剛度矩陣；最后，對所有單元總體集成得到總體剛度矩陣[11?15]。

2.1 網格剖分及插值

首先在研究區域內進行矩形單元剖分。為了提高計算精度及減小利用式(6)～(9)求解時帶來的誤差，本文采用精度較高的雙二次插值進行模擬。圖2所示為坐標變換關系及局部節點編號，其中圖 2(a)所示為母單元，圖2(b)所示為子單元；a和b分別表示子單元的寬度及高度；(x0，z0)為矩形單元中心點的坐標。文中采用的插值函數表示如下：

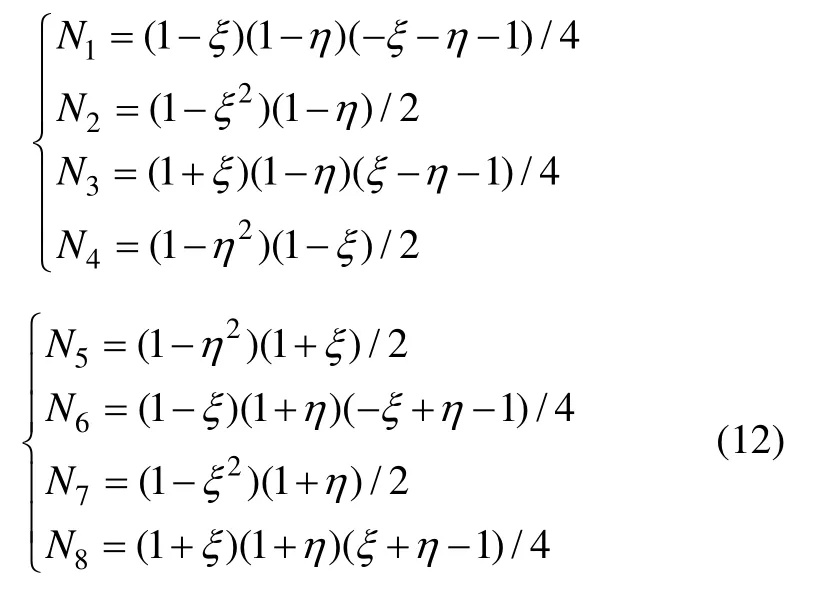
圖2 矩形單元剖分示意圖Fig. 2 Schematic diagram of rectangle meshing element

子單元與母單元之間的坐標變換關系式表示如下：

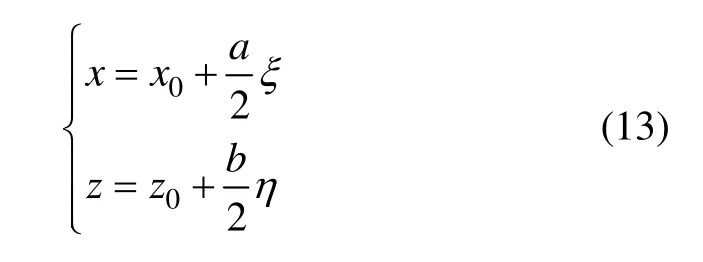
2.2 單元分析

首先對式(10)進行單元分析。

記U1=(u1，u2，…，u8)T，V1=(v1，v3，…，v8)T，則

式(10)中左邊第1項：

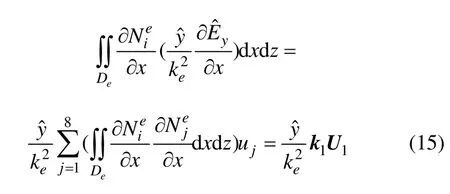
式(10)中左邊第2項：

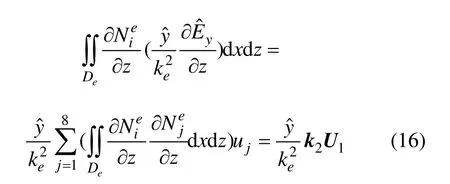
式(10)中左邊第3項：

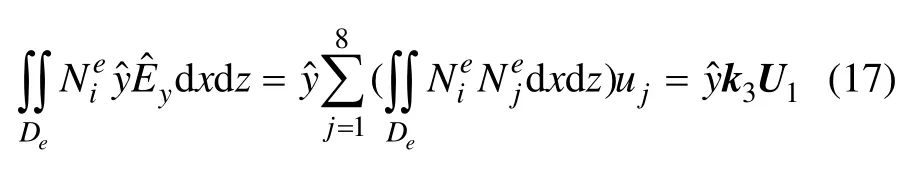
式(10)中左邊第4項：

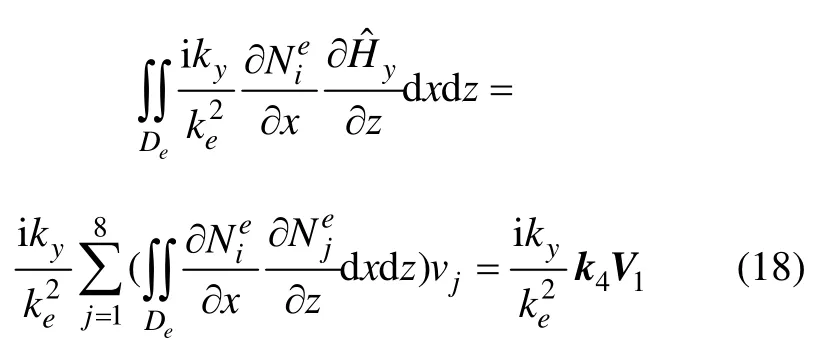
式(10)中左邊第5項：

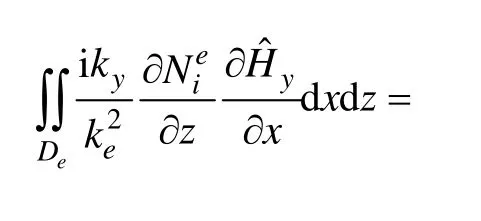
再對式(11)進行單元分析。

式(11)中左邊第1項：

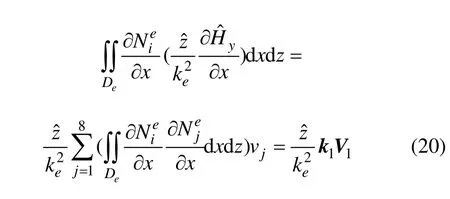
式(11)中左邊第2項：

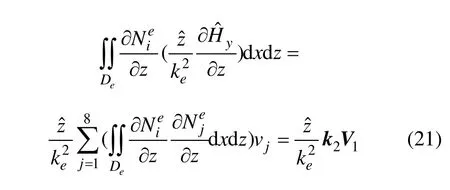
式(11)中左邊第3項：

式(11)中左邊第4項：

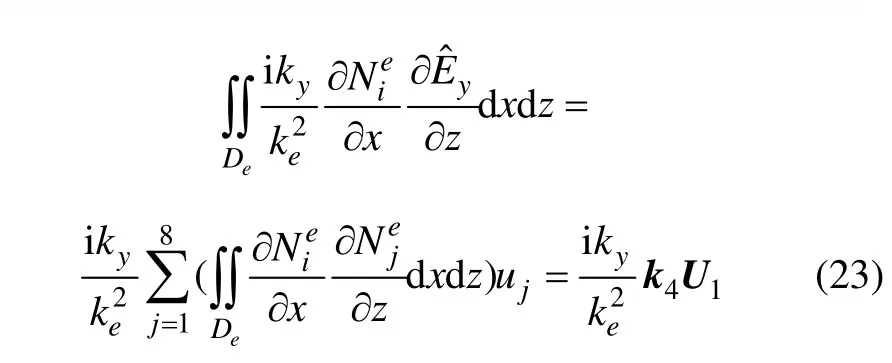
式(11)中左邊第5項：

觀察式(15)～(24)，借助符號計算工具maple可求得：

2.3 總體合成

將式(15)～(19)中各項累加，從而可將式(10)化為

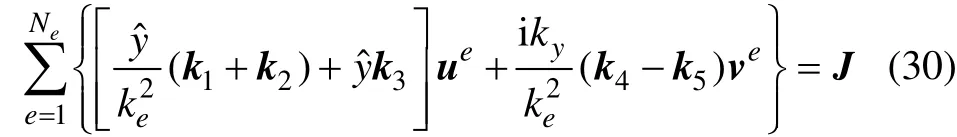
其中：J代表電流源項。將式(20)～(24)中各項累加，從而可將式(11)化為

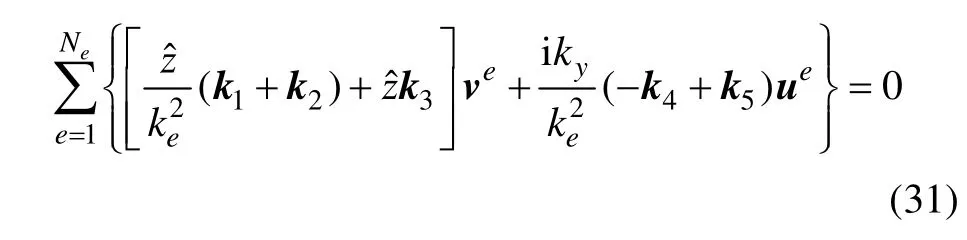
再對式(30)及(31)化簡，令

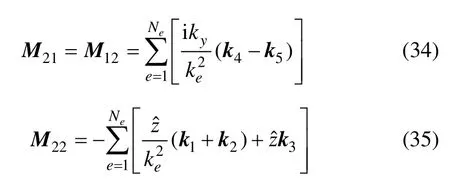
則式(30)和(31)可記為：

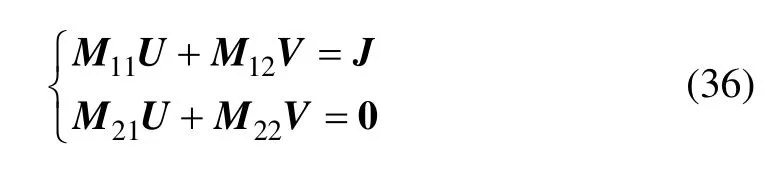
將式(36)等價為

將式(37)中左邊的剛度矩陣記作

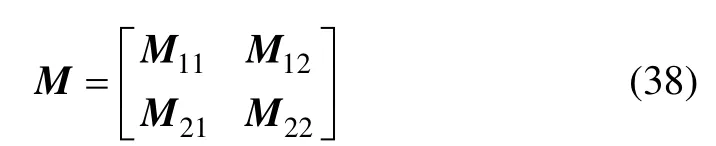
經分析可知：M矩陣為復對稱矩陣。求解線性方程組(38)即可得到傅氏域的 2個電磁場分量，再利用式(6)～(9)求得傅氏域中的其余4個電磁場分量；最后，利用傅里葉逆變換求得各個電磁場分量。

3 波數的選取

2.5 維數值模擬是先在波數域里計算電磁場，再通過傅里葉逆變換求得空間域的電磁場。由于在數值模擬時不可能取無窮多個波數來還原真實的電磁場，因此，需要選取若干個合適的波數以盡可能、快速地求得真實的電磁場。如何選取波數及確定波數的選取范圍便是一個關鍵性問題。

本文通過實際計算及分析，選取一組兼顧計算速度與精度的波數。在收發距為4 km，頻率f為2 Hz和1 024 Hz時，分別進行正演模擬計算并繪制了及隨波數的變化曲線圖，如圖3所示。其中，圖3(a)所示為隨波數的變化曲線圖，圖3(b)所示為隨波數的變化曲線圖。從圖3(a)可知：當波數較小時，基本保持不變；隨著波數繼續增大時，開始下降；當波數約為0.01時到達波谷，而后又稍有回升。由圖 3(b)可知：當波數較小時，很小；隨著波數增大，開始先上升，到達波峰后以較陡傾角下降；同樣地，當波數約為0.01時到達低谷，而后又稍有回升，但變化曲線沒有規律。據文獻[6]，波谷右側的曲線是不可靠的。事實上，曲線到達波谷后繼續往下遞減，且由于此時取值已經很小，對傅里葉逆變換中的積分結果的影響可以忽略，因此，只需要在波谷左邊部分選取足夠的能夠精確計算積分的一組波數即可。本文通過不斷進行正演計算及對比分析，選取由20個波數構成的一組波數，如表1所示。

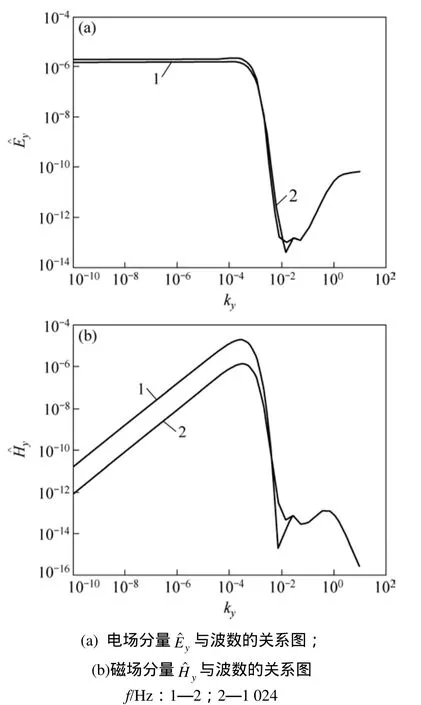
圖3 傅氏域中電場和磁場隨波數變化示意圖Fig. 3 Schematic diagram of electric field and magnetic field in Fourier domain of changing with wave number

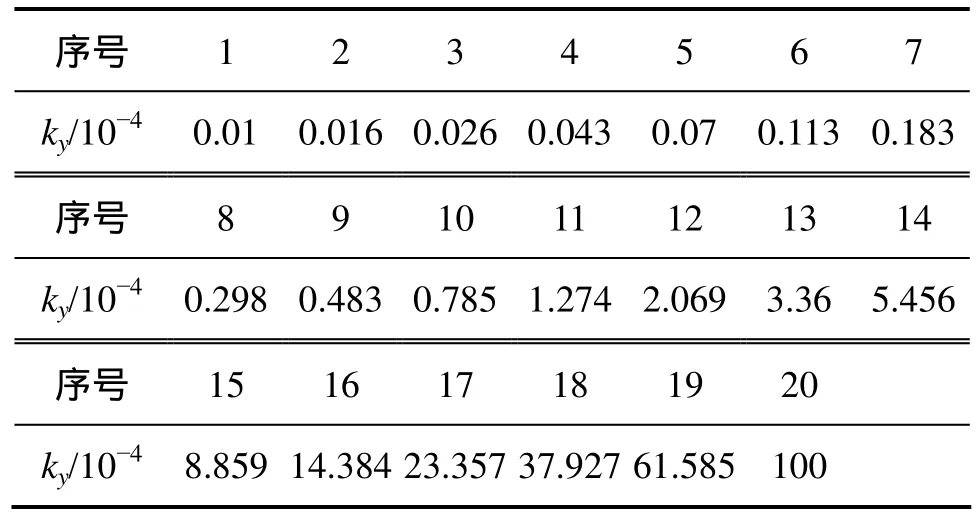
表1 波數值選取Table 1 Choice of wavenumbers

事實驗證，這一組波數能夠有效且快速、精確計算2.5維FCSEM的電磁場響應。本文后續的工作都是基于這一組波數進行的。

4 數值算例

4.1 算法驗證

為了驗證本文算法的正確性，對1個電阻率為100?·m的均勻半空間模型進行正演模擬計算及與解析解的對比分析。圖4所示為解析解與數值解對比結果圖(其中，x軸代表的是收發距)。由圖4可知：電磁場分量數值解與解析解相吻合，且頻率低時精度更高。計算結果表明：對于電場分量，當f=2 Hz時，最小相對誤差為 0.106%，最大相對誤差為 0.639%，平均相對誤差為0.460%；當f=1 024 Hz時，最小相對誤差為0.451%，最大相對誤差為 1.763%，平均相對誤差為0.920%。對于磁場分量，當f=2 Hz時，最小相對誤差為 0.016%，最大相對誤差為 0.513%，平均相對誤差為0.220%；當f=1 024 Hz時，最小相對誤差為0.545%，最大相對誤差為 1.921%，平均相對誤差為 1.028%。可見，完全滿足正演計算的要求。

4.2 模型計算

4.2.1 低阻體模型

圖5所示為 1個低阻體模型的示意圖，其中，x方向標出的刻度代表垂直收發距。圖6和圖7所示為正演模擬結果。其中，圖6(a)和圖6(b)所示分別為TE模式下的視電阻率及相位等值線圖，這2個圖中都反映出了異常，且異常的中心位置與理論模型一致，異常都有往右下方拉長的趨勢，這正是場源陰影效應的影響；視電阻率等值線圖異常最低為30 ?·m，接近異常體的真實值。圖7(a)和圖7(b)所示分別為TM模式下的視電阻率及相位等值線圖，這2個圖中也都反映出了異常，且相比 TE模式異常垂向拉長明顯。這是由于TM模式下測定的是電場的法向分量，界面積累電荷效應使得受靜態效應明顯，造成垂向拉長，這提高了方法的靈敏度，有利于發現小規模低阻體，故TM模式發現異常的能力比TE模式的強。

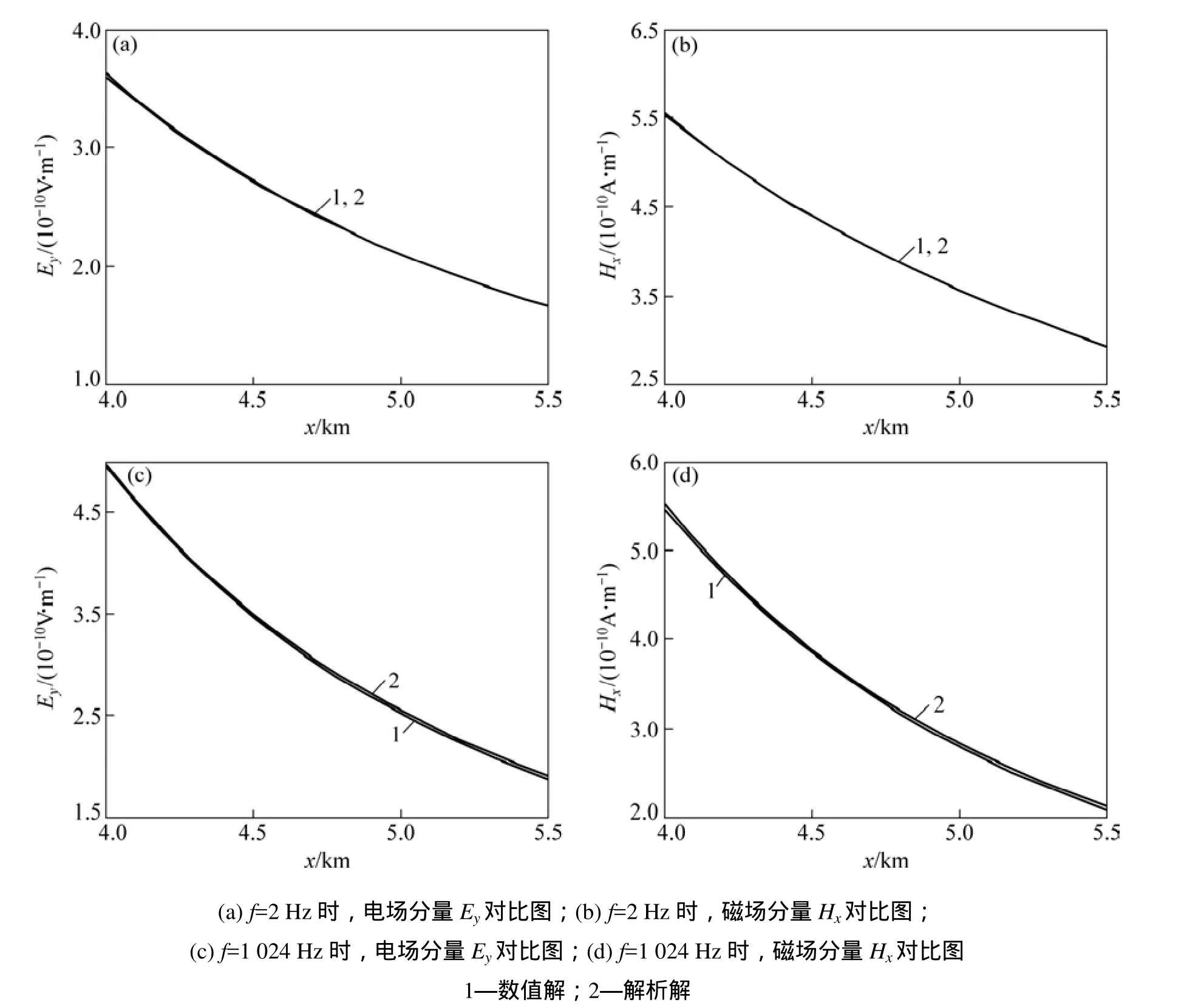
圖4 均勻半空間模型解析解與數值解對比結果Fig. 4 Comparison between analytic solution and numerical solution of homogenous half space

圖5 低阻體模型示意圖Fig. 5 Schematic diagram of low resistivity body

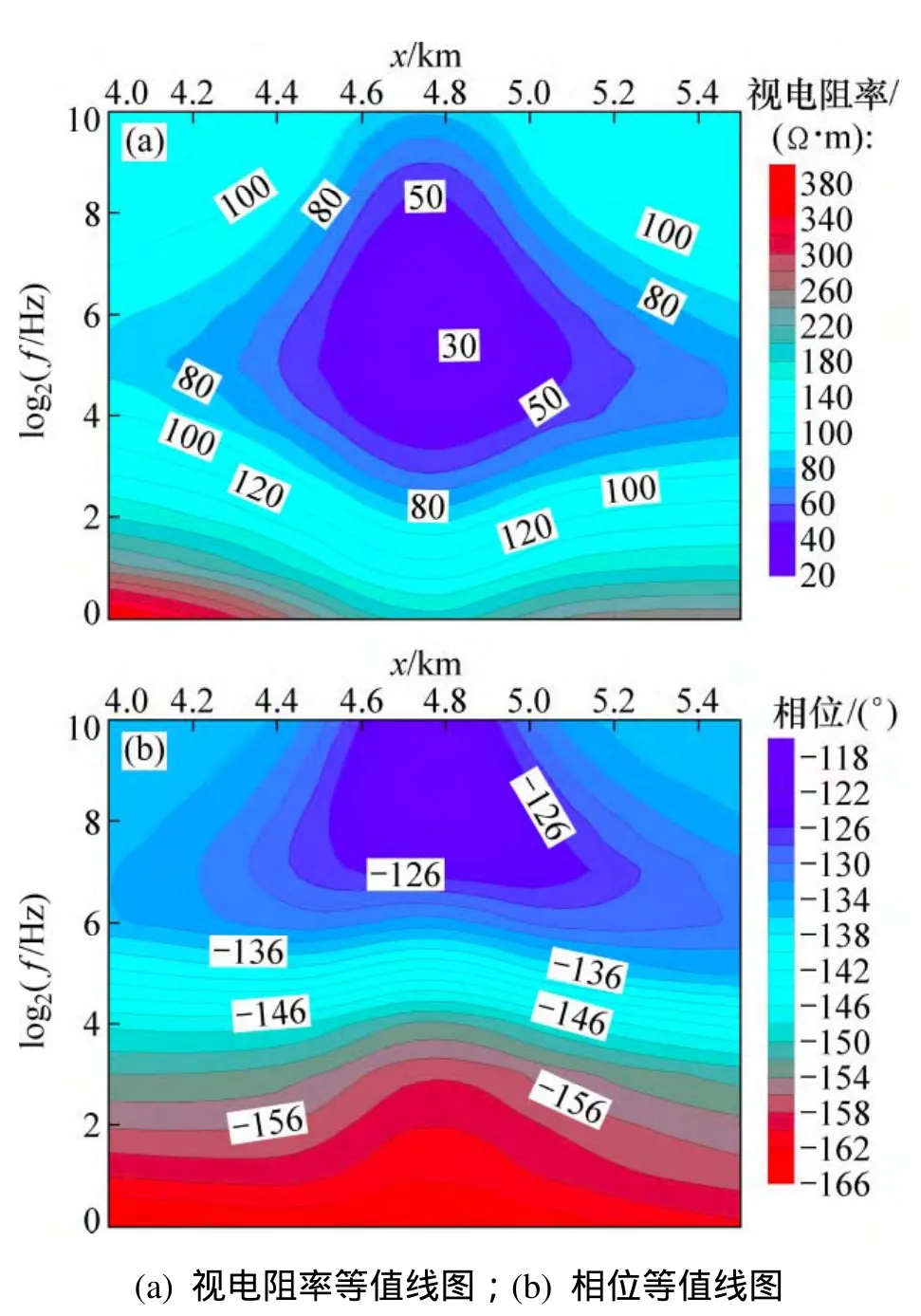
圖6 TE模式下低阻體模擬結果Fig. 6 Schematic simulation result of low resistivity body of TE mode

4.2.2 高阻體模型

圖7 TM模式下低阻體模擬結果Fig. 7 Simulation results of low resistivity body of TM mode

圖8 高阻體模型示意圖Fig. 8 Schematic diagram of high resistivity body

圖8 所示為1個高阻體模型的示意圖，圖9和圖10所示為正演模擬結果。其中，圖9(a)和(b)所示分別為TE模式下的視電阻率及相位等值線圖，這2個圖中都反映出了異常，視電阻率等值線圖中異常最高為130 ?·m，而真實異常為500 ?·m，說明頻率域可控源電磁對高阻體反映不靈敏，這是電磁法類勘探方法普遍存在的一個問題。圖 10(a)和 10(b)所示分別為 TM模式下的視電阻率及相位等值線圖，這2個圖中都反映出異常，視電阻率等值線圖中異常最高為200 ?·m，說明TM模式較TE模式對高阻體反映較靈敏。

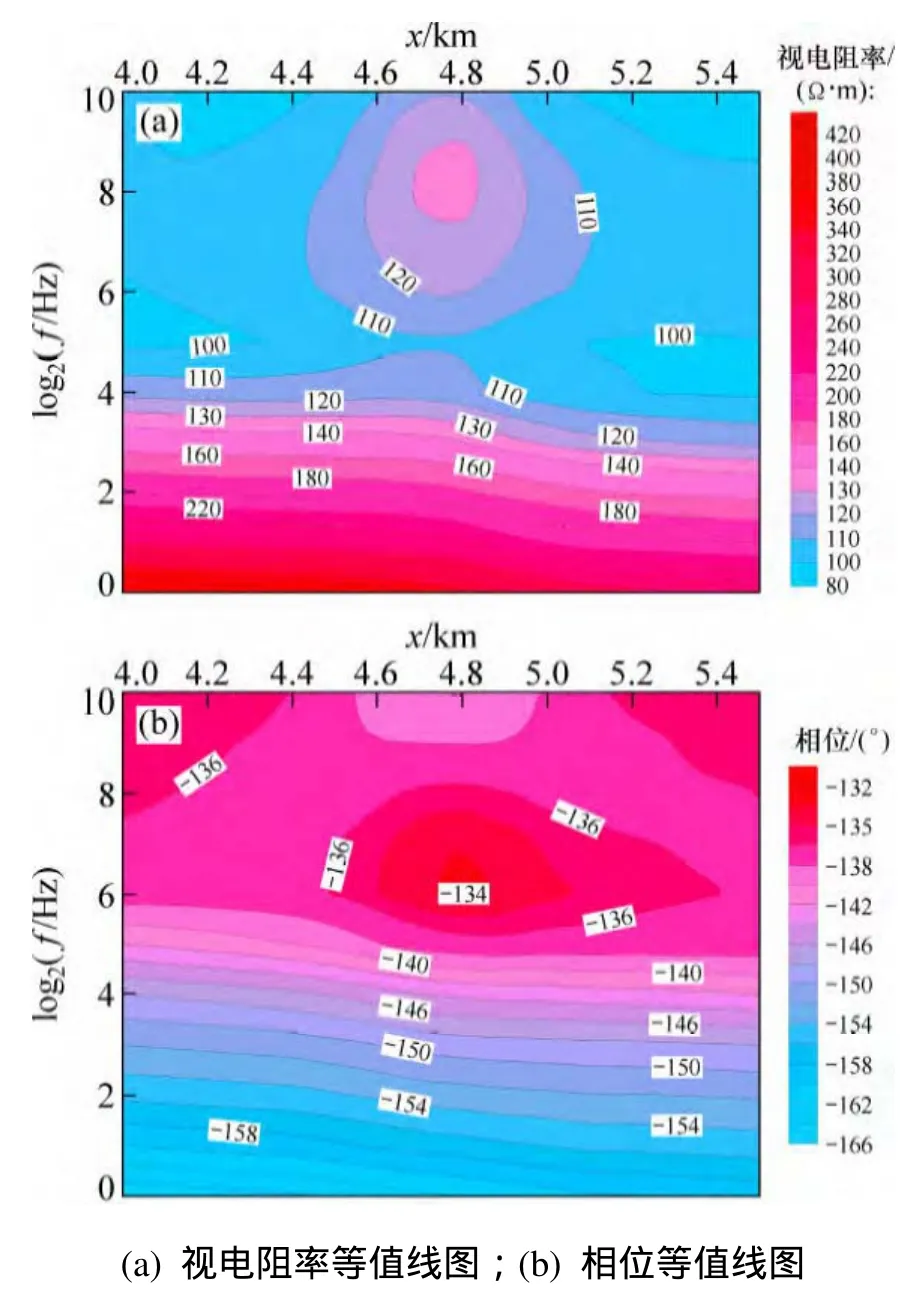
圖9 TE模式下高阻體模擬結果Fig. 9 Simulation results of high resistivity body of TE mode

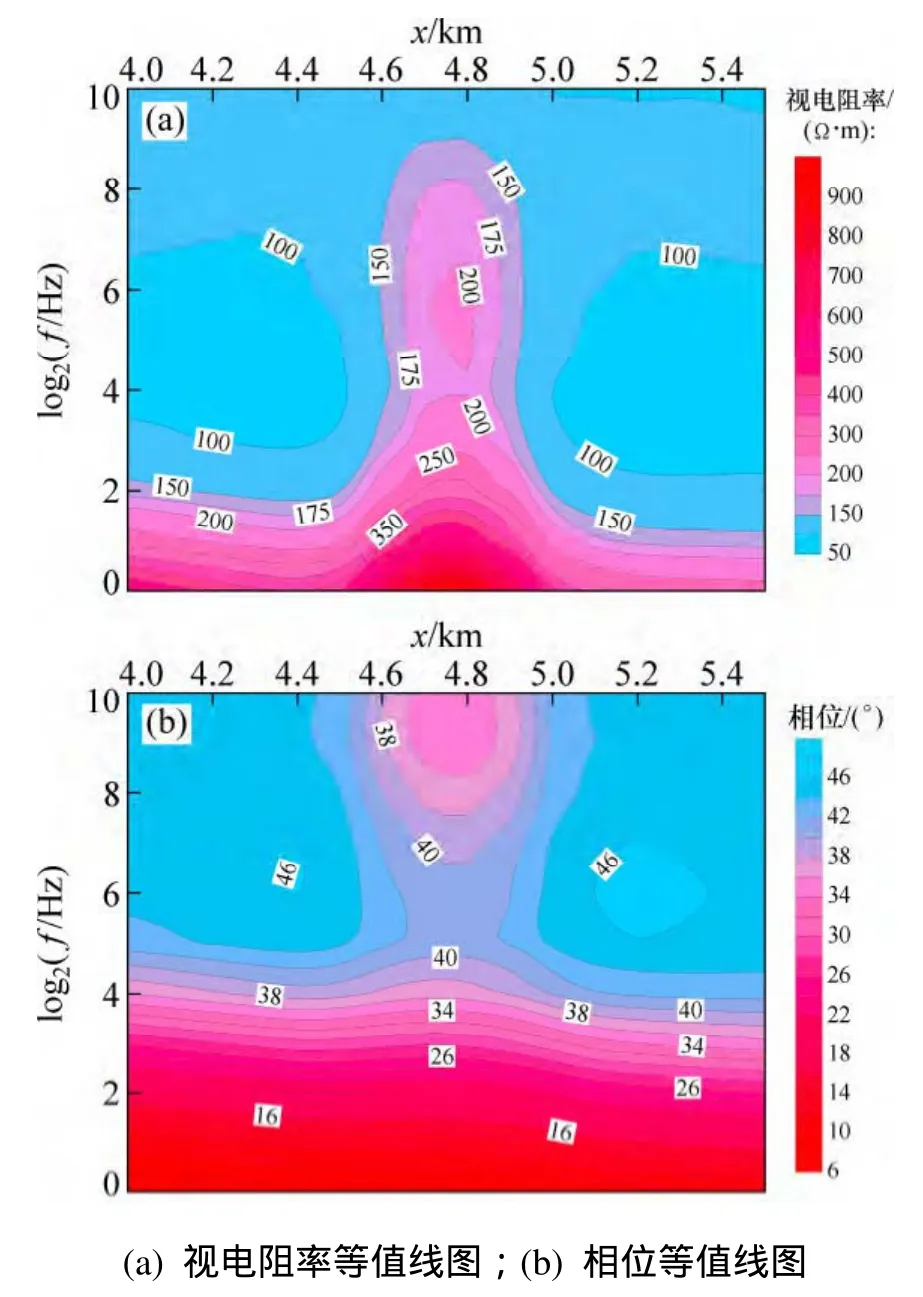
圖10 TM模式下高阻體模擬結果Fig. 10 Simulation results of high resistivity body of TM mode

5 結論

(1) 通過均勻半空間模型下低頻及高頻時的有限元數值解與解析解對比，結果顯示有限元數值解與解析解基本吻合，從而從一定程度上驗證了基于雙二次插值的2.5維FCSEM正演模擬算法的正確性。

(2) 本文2.5維FCSEM有限元數值模擬結果能夠正確反映二維模型的淺部異常及構造，進一步驗證了該算法的可靠性，可以有效地模擬2.5維地電模型。

(3) TM模式下低阻及高阻異常體響應均有往下拉長的趨勢，對低阻及高阻異常體反應較TE模式明顯，且橫向分辨能力更強。

[1]底青云, 王若. 可控源音頻大地電磁數據正反演及方法應用[M]. 北京: 科學出版社, 2008: 74?84.DI Qingyun, WANG Ruo. Forward modeling and inversion of CSAMT data and its application in earth[M]. Beijing: Science Press, 2008: 74?84.

[2]湯井田, 何繼善. 可控源音頻大地電磁法及其應用[M]. 長沙:中南大學出版社, 2005: 9?33.TANG Jingtian, HE Jishan. Audio-frequency of controlled source electromagnetic method and its application in earth[M].Changsha: Central South University Press, 2005: 9?33.

[3]米薩克 N 納比吉安. 勘查地球物理電磁法. 1卷: 理論)[M].趙經祥, 王艷君, 譯. 北京: 地質出版社, 1992: 330?333.Nabighian M. Electromagnetic methods in applied geophysics:Ⅰ. Theory[M]. ZHAO Jingxiang, WANG Yanjun, trans. Beijing:Geological Publishing House, 1992: 330?333.

[4]熊彬. 關于瞬變電磁法2.5維正演中的幾個問題[J]. 物探化探計算技術, 2005, 28(2): 124?128.XIONG Bin. Several problems related to 2.5 dimensional forward modeling of transient electromagnetic method[J].Computing Techniques for Geophysical and Geochemical Exploration, 2005, 28(2): 124?128.

[5]Unsworth M J, Travis B J, Chave A D. Electromagnetic induction by a finite electric dipole source over a 2-D earth[J].Geophysics, 1993, 58(2): 198?214.

[6]Mitsuhata Y. 2-D electromagnetic modeling by finite-element method with a dipole source and topography[J]. Geophysics,2000, 65(2): 465?475.

[7]底青云, Unsworth M, 王妙月. 復雜介質有限元法2.5維可控源音頻大地電磁法數值模擬[J]. 地球物理學報, 2004, 47(4):723?730.DI Qingyun, Unsworth M, WANG Miaoyue. 2.5 D CSAMT modeling with the finite element method over 2D complex earth media[J]. Journal of Geophysics, 2004, 47(4): 723?730.

[8]底青云, Unsworth M, 王妙月. 有限元法2.5維CSAMT數值模擬[J]. 地球物理學進展, 2004, 19(2): 317?324.DI Qingyun, Unsworth M, WANG Miaoyue. 2.5 D CSAMT modeling with finite element method[J]. Progress in Geophysics,2004, 19(2): 317?324.

[9]薛東川, 戴世坤. 頻率域2.5維電磁測深有限元模擬中的吸收邊界條件[J]. 中國石油大學學報(自然科學版), 2008, 32(6):57?61.XUE Dongchuan, DAI Shikun. Absorbing boundary condition for simulating 2.5-D electromagnetic sounding in frequency domain by finite element method[J]. Journal of China University o f Petroleum (Natural Science Edition), 2008, 32(6): 57?61.

[10]王華軍, 羅延鐘. 中心回線瞬變電磁法2.5維有限單元算法[J].地球物理學報, 2003, 46(6): 855?862.WANG Huajun, LUO Yanzhong. Algorithm of a 2.5 dimensional finite element method for transient electromagnetic with a central loop[J]. Journal of Geophysics, 2003, 46(6):855?862.

[11]TONG Xiaozhong, LIU Jianxin, XIE Wei, et al.Three-dimensional forward modeling for magnetotelluric sounding by finite element method[J]. Journal of Central South University of Technology, 2009, 16(1): 136?142.

[12]柳建新, 蔣鵬飛, 童孝忠, 等. 不完全 LU 分解預處理的BICGSTAB算法在大地電磁二維正演模擬中的應用[J]. 中南大學學報(自然科學版), 2009, 40(2): 484?491.LIU Jianxin, JIANG Pengfei, TONG Xiaozhong, et al.Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 484?491.

[13]TANG Jingtian, WANG Feiyan, REN Zheng-yong, et al. 3-D direct current resistivity forward modeling by adaptive multigrid finite element method[J]. Journal of Central South University of Technology, 2010, 17(3): 587?592.

[14]劉長生, 湯井田, 任政勇, 等. 基于非結構化網格的三維大地電磁自適應矢量有限元模擬[J]. 中南大學學報(自然科學版),2010, 41(5): 1855?1859.LIU Changsheng, TANG Jingtian, REN Zhengyong, et al.Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J]. Journal of Central South University (Science and Technology), 2010, 41(5):1855?1859.

[15]張繼鋒, 湯井田, 王燁, 等. 基于預處理共軛梯度的大地電磁快速正演[J]. 中南大學學報(自然科學版), 2010, 41(5):1877?1882.ZHANG Jifeng, TANG Jingtian, WANG Ye, et al.Magnetotellurics fast forward based on preconditioning conjugate gradient[J]. Journal of Central South University(Science and Technology), 2010, 41(5): 1855?1859.