《線性代數》教學中學生創新意識和創新精神的培養
潘大勇,陳忠
(長江大學信息與數學學院,湖北 荊州434023)
《線性代數》是高等院校普遍開設的一門重要的必修基礎課,在現代物理、化學、計算機科學、通訊技術、工商管理、資源勘查、石油工程等領域的應用越來越廣泛,發揮無可替代的重要作用。教學過程中,在傳授基礎知識、基本方法和基本技能的同時,如何著力培養學生的創新意識和創新精神,是每個教師在教學中都應當認真思考的重要課題。
1 在新舊知識的銜接處培養學生的創新意識和創新精神
在講授知識過程中,要引導學生感受 《線性代數》中的一些概念和方法是如何產生出來的,感受學科發展過程中孕育的創新精神和力量。
解線性方程組是 《線性代數》的一個中心課題,是 《線性代數》發展的原動力之一。行列式的概念就是在求解二元一次線性方程組、三元一次線性方程組(方程的個數和未知數的個數相同)所使用的高斯消元法的基礎上引入的。如果只是簡單地告訴學生結論,而置知識產生的背景和萌生的思想而不顧,學生就難以理解要引入一個新的概念和方法的必要性。因此,讓學生感知創新意識的土壤在哪里是很重要的。如果理解了二階、三階行列式的實質,學生自然而然就能理解一般意義的n階行列式了。
探究發現,克萊姆(Cramer)法則只能解決方程個數與未知數個數相同的線性方程組的情形,而且對于解不唯一時怎么表示通解等都有很大的局限性,這就會引發新的思考和探究,如何才能更一般地解決線性方程組的求解問題?引入矩陣及初等變換這個新的工具,學生就能理解這樣做的必要了。借助矩陣的初等變換和矩陣的秩,不僅可以判別一般的線性方程組的解的存在性,而且可以給出解的表達式。對于線性方程組有無窮多解的情形,解與解之間的關系如何呢?如何表示解之間的關系呢?換句話說,能否用有限多個解去表示無窮多個解呢?這樣的問題又可引發出向量組的線性相關性理論和線性方程組解的結構理論。這樣一種在新舊知識交匯銜接處提出問題,滲透創新意識,培養創新精神都是大有潛力可以發掘的。
2 在探究知識的過程中培養學生的創新意識和創新精神
在通常的教材中,《線性代數》都是演繹結構,每章(節)大致上是按定義、性質、定理或公式、求解等基本環節來呈現[1-2]。演繹體系邏輯性強,條理脈絡清晰,內容緊湊精煉,但不可回避的是,學生往往覺得難以理解并有種壓迫感,和書本產生很強的距離感,總會有一個個問題縈繞在心頭:編著者為什么這樣寫呢?這些結果是怎么想到的呢?如果能夠將數學家在建構相關知識時所作的 “火熱思考”[3]再現出來,學生學到的不僅僅是一些結果,而且能夠感受數學家的創新思維過程。
矩陣是 《線性代數》的核心概念,那么為什么會有這樣一個概念呢?矩陣的本質是什么?矩陣其實就是一個數表,存在于生活的方方面面。上課的課表、成績單(文字本質上也可以數字化)、科研數據等各種表格以及照片(黑白照片從數學角度看其實是一個數表,每個點都可以用0~255中某個整數表示其灰度值,彩色照片則是由紅綠藍3種基色復合而成的三維的數表)等等都可以用矩陣表示。既然用矩陣表示數表,那么是否可以用矩陣來描述數表的運動變換呢?如把一張圖片放大2倍,或是把一張圖片逆時針旋轉90°,等等,這就涉及到矩陣的運算及其性質了。這些內容對于第一次接觸的學生而言,好比當年數學家們首先發現、探究一樣,是一種全新的挑戰,是一次創新之旅,無論是方法還是思想,無不深深闡發出創新的精神,這對學生的創新意識的影響是重要和深遠的。學生重走前人的路,并不是簡單的重復,其實也是一次發現之旅,探索之旅,創新體驗之旅,成長收獲之旅。從這個意義上講,老師的引導和啟迪是十分關鍵的,如果教師滿堂灌,學生缺少獨立思維活動,其實就是剝奪了學生的創新意識的產生。如果所有結論總是以完整的形式出現,學生知其然,而不知其所以然,體驗不到探索和發現的過程,長此以往,不利于學生發現、探索能力的培養,也不利于學生抽象、歸納、概括能力的培養,更不利于創新意識和創新精神的培養。
3 在應用知識解決問題的情境中培養學生的創新思維意識
當前,《線性代數》的教學相對偏重自身的理論體系,強調基本定義、定理和基本思想,實際應用講的較少,應用類的課后習題也少得可憐.這導致大部分學生不了解線性代數對后續專業課學習,也在一定程度上影響專業課的學習質量[4]。因此,《線性代數》的學習,不單是培養學生的邏輯思維能力,而且還應當重視它的廣泛應用,在應用中鍛煉學生的數學眼光和數學思考,培養學生發現并提出相應的數學問題(或數學模型)的意識,應用數學方法去解決問題的能力。教學中要秉承這樣的理念,提升應用意識。
以矩陣乘法和線性變換這個知識點為例,在教學中可以結合具體問題來激發學生創新思維的 “火熱思考”。如:
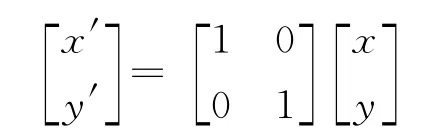

還可以設計更多的類似問題,如旋轉變換:
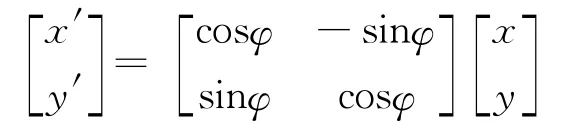

進一步可以推廣到更一般的情形:即利用矩陣Am×n,將n維向量轉化為m向量(特別是在二維和三維向量之間進行轉換,即平面圖形和空間圖形之間的轉換)。
此外,還可以結合一些數學軟件(如Matlab)直觀再現上述的各種變換,這些應用就把所學的知識變得生動而有趣,這也是 《線性代數》的魅力所在。
4 結語
在線性代數的教學中培養學生的創新意識和創新精神不是一朝一夕的事情,應該有一個比較全面的教學安排,落實到教學的每一個環節。在教學內容的起始處引導學生感悟新概念、新方法與其萌生的背景之間的關聯,感受創新意識的激發是內在和外在需要的共同結果;在講授環節中探究相關知識的創新歷程,體會創新思維的某些特征和規律;在應用知識的過程中培養學生創新意識,提高學生解決問題的能力。
[1]同濟大學數學系.線性代數 [M].北京:高等教育出版社,2007.
[2]李克娥,吳海濤.線性代數 [M].武漢:華中科技大學出版社,2013.
[3]張奠宙.微積分教學:從冰冷的美麗到火熱的思考 [J].高等數學研究,2006(2):4-6.
[4]藍洋.吳香艷.電子信息學科中線性代數的教學方法探討 [J].電子設計工程,2012(13):40-42.

