混響干擾下的潛艇目標尺度識別

董仲臣，李亞安，劉望生

(1.西北工業大學 航海學院，陜西 西安710072;2.中國人民解放軍91388 部隊，廣東 湛江524022;3.浙江理工大學 機械與控制學院，浙江 杭州310018)

0 引 言

魚雷自導系統在工作時，有2 種海洋背景干擾［1］:一種與魚雷發射信號無關，由魚雷自噪聲和海洋環境噪聲形成的噪聲;另一種與魚雷發射信號有關，是海洋中大量無規則散射體對入射信號產生的散射波在接收點疊加而形成的混響［1-2］。對于魚雷主動自導系統，在淺海環境下，混響成為主要的背景干擾，嚴重影響了自導系統的性能［1，3］。并且，潛艇可以使用各種類型的水聲對抗器材對魚雷的攻擊實施對抗，大大降低了魚雷的攻擊能力。所以，魚雷自導系統應該具備混響干擾下對潛艇目標和誘餌進行識別的能力，從而能正確地對真實目標進行打擊［4］。

本文在建立混響條件下潛艇目標亮點模型的基礎上，提出一種混響干擾下潛艇目標識別方法。該方法用自身多普勒抑制技術對帶有混響的回波進行混響抑制，并采用MUSIC 算法對潛艇目標亮點進行方位估計，從而實現對潛艇目標的尺度識別。仿真結果表明，該方法能夠很好地實現對潛艇目標的尺度識別。

1 混響干擾下的潛艇目標亮點模型

1.1 混響信號仿真

為了體現魚雷運動對混響信號的影響，本文對單元散射混響模型［2，5］進行改進，把產生混響的海底劃分成若干散射單元，每個散射單元都能散射出具有一定多普勒頻移的散射波，則混響信號等于發射信號通過各個散射單元產生響應的總和。利用該方法進行仿真，可以根據需要把散射單元劃分到足夠小，因此魚雷相對每個散射單元的多普勒頻移相同，從而比較準確的體現魚雷運動對混響信號的影響。散射單元的劃分如圖1所示。

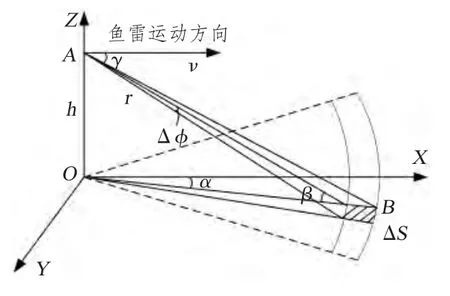
圖1 散射單元劃分示意圖Fig.1 Scatteringunit classification diagram

t 時刻，對混響有貢獻的區域為如圖1 中圓環。把此圓環分割成若干散射單元，魚雷到散射單元的距離為r，散射單元的面積為ΔS，散射單元對應的圓心角為Δφ。魚雷以速度v 沿著X 軸運動，魚雷距離海底為h，散射單元與魚雷速度方向的夾角為γ，相對于魚雷的仰俯角為β，與X軸的夾角為α。

散射單元的面積ΔS 可由式(1)求得:

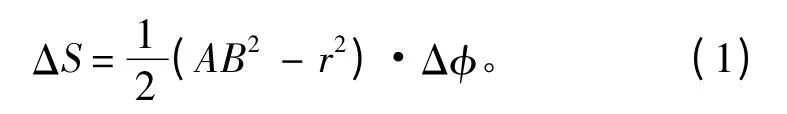
其中:AB2=cτ/2，r=(c(t－τ))/2，τ 為魚雷主動聲脈沖寬度。

第i 個散射單元的響應為:

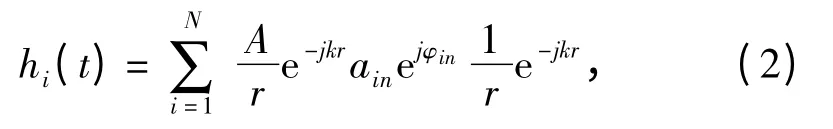
對式(2)進行整理得:

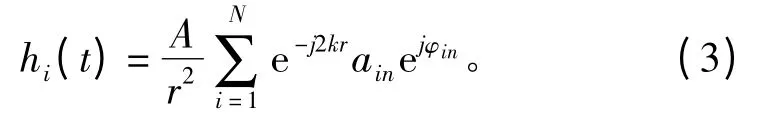
式中:A 為發射信號強度;N 為單元內散射體的數量;k 為波數，k=2πf/c;為散射體的散射系數，隨機振幅ain和隨機相位φin都按高斯分布［5］。

N 可由式(4)求得:

其中ρ 為單位面積散射體的數量。

考慮魚雷運動帶來的多普勒頻移時，假定散射單元足夠小，所以對于每個散射單元，散射波的多普勒頻移相同，多普勒頻移為:

式中:f 為入射波頻率;c 為水中聲速。當海區條件為淺海時，魚雷到海底的距離h 很小，所以此時把β近似為0 可以簡化仿真，則式(5)變為:

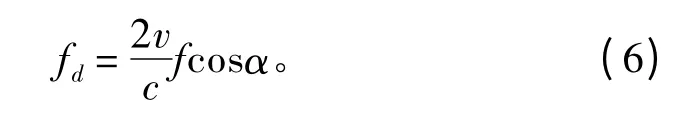
設魚雷發射的主動信號為s(t)，在每個散射單元上產生的混響為:

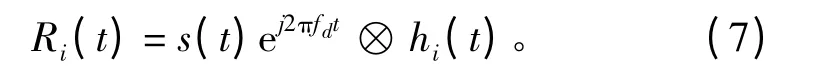
其中?為卷積運算。

則t 時刻產生的混響為發射信號通過各個系統的疊加:

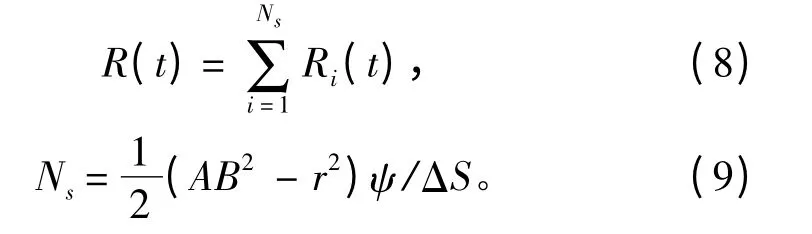
式中:Ns為散射單元的數量;ψ 為魚雷自導系統方位角束寬。

1.2 潛艇目標亮點模型

理論分析和實驗結果表明，在高頻情況下，任何一個目標的回波都是由若干個子回波迭加而成，而每個子回波都可認為是從某個散射點發出的，這個散射點就是亮點。亮點可以真實存在，也可以是等效。這樣，任何一個目標都可以等效成若干個亮點的組合，每個亮點產生一個回波，所以，目標總的回波是這些亮點回波的迭加［6-7］。

在目標回波中有3 個重要的特征，即目標回波的時間展寬、目標回波的亮點起伏和目標回波空間方位分布。這3 個特征是對目標進行識別的重要依據，且在實驗中已證實了它們的存在。所以，1 個完整的目標回波模型可以由幅度因子、時延和相位跳變3 個參量確定［6-8］。單個亮點的傳遞函數可表示為:

式中:r 為魚雷到目標亮點的距離;Ai(r，θ，ψ)為該亮點回波的幅度，它與目標的距離r 和聲波入射方向，即照射角θ 和俯仰角ψ 有關;τi為該亮點的時延，由等效聲中心相對于某個參考點的聲程決定，且是θ 的函數;ω(v)為由于目標的相對運動，造成回波的中心頻率與入射波的中心頻率相差一個多普勒頻移;φ 為回波形成時的相位跳變。

因此，潛艇目標總的傳遞函數為:

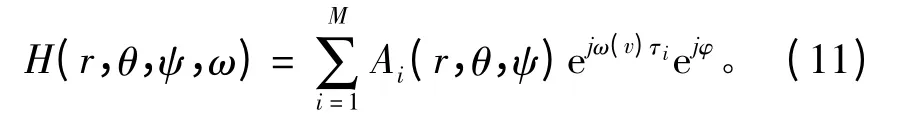
其中M 為目標亮點的個數。

設魚雷發射的窄帶脈沖信號為

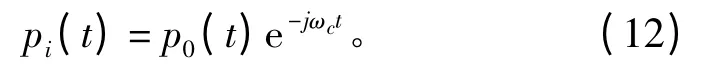
式中:ωc為載頻;p0(t)為包絡，它只在脈沖持續時間內有值。

無論目標多么復雜，在遠場中散射波都以exp(jkr)/r 的規律擴展，k 為波數。取目標亮點個數為3，得到的回波為:

其中ωd為潛艇和魚雷相對運動產生的多普勒頻移。由于魚雷已經對自身運動產生的多普勒進行了補償，因此只需考慮潛艇運動產生的多普勒頻移:

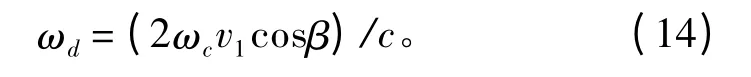
其中v1為潛艇運動速度。

對于潛艇上曲率面積較小的反射點，由于目標強度較小，仿真時可以隨機噪聲n(t)來代替。則式(14)變為:

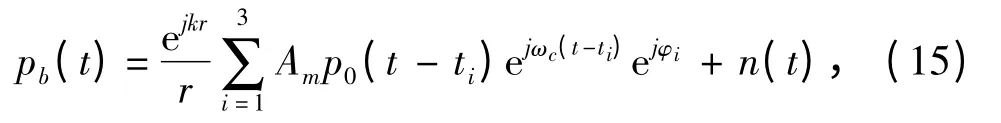
亮點回波的幅度為

假設聲波以照射角θ入射時，由于魚雷的聲脈沖發射周期很短，可認為在一個聲脈沖發射周期內魚雷與潛艇的相對距離不變。則第i 個亮點的時延為:

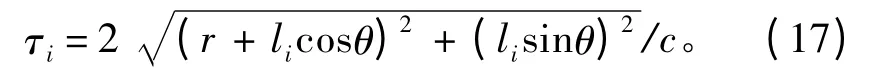
式中:r 為魚雷與潛艇距離，即魚雷與代表艦首的亮點距離;θ 為照射角;li為亮點與艦首的距離。

由于入射聲波遇到亮點后反射，在回波信號中引入相位跳變φi，它是一個在(0，2π)中均勻分布的隨機變量，則混響干擾下的潛艇目標亮點回波信號為:

2 混響干擾下的目標尺度識別

對于帶有混響信號的回波信號，本文先用自身多普勒抑制技術行混響抑制，然后采用MUSIC 算法，對潛艇的目標亮點進行方位估計，從而實現對潛艇目標的尺度識別［9-11］。

2.1 混響抑制

對魚雷來講，自身多普勒抑制技術是行之有效的抗混響技術，它主要是利用混響信號與目標回波多普勒頻移的差異來對混響進行抑制。

分布于海洋中和界面上的散射體都是混響的來源。這些散射體都有一個共同特征，即均為固定不動或者運動速度很小。因此在淺海環境下，混響信號與目標回波多普勒頻移量的差別是抗混響可利用的信息。

混響信號的頻率與速度為0 時的目標回波頻率相近，而魚雷所攻擊的目標一般具有一定的運動速度，所以，利用混響頻率與目標回波頻率的差別設計一多普勒門，當接收信號頻率未達到一定范圍時，多普勒門關閉，使混響難以通過，從而達到抑制混響的目的。多普勒門的實現可以通過設計特性頻率響應的濾波器來實現。

2.2 目標尺度識別

為了對混響抑制后的潛艇目標回波進行方位估計，現 采 用 MUSIC 算 法 ( Multiple Signal Classification Algorithm)來實現潛艇目標的尺度識別。MUSIC 算法通常又稱多重信號分類方法，是根據接收數據的協方差矩陣，分離出信號子空間和噪聲子空間，利用信號方向向量與噪聲子空間的正交性，來構成空間掃描譜，實現信號的方位估計。

對于一個由M 個陣元組成的已知任意集合形狀矩陣，假設有D(D ＜M)個遠場窄帶信號(中心頻率為f0)，信號源從D 個方向ΘD=［φ1，φ2，…，φD］入射到該基陣。這M 個陣元的接收信號寫成矩陣形式為

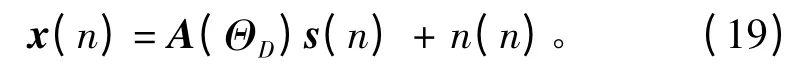
式中:A(ΘD)=［a(φ1)，a(φ2)，…，a(φD)］為M ×D 維陣列流行矩陣;s(n)=［s1(n)，s2(n)，…，sD(n)］為D ×1 維信號源向量;n(n)為M ×1 維噪聲向量。

數據協方差矩陣可以表示為

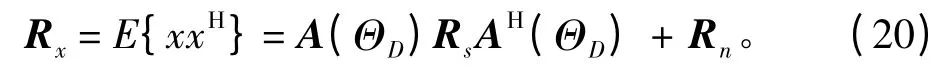
其中Rs和Rn分別為D ×D 維信號協方差矩陣與M ×M 維噪聲協方差矩陣，即

對協方差矩陣Rx進行特征分解，可將

式中:Λ 為降序排列的特征值構成的對角陣;E=［Es，En］為對應的特征值，Es與En分別是由較大的D 個特征值和較小的M－D 個特征值對應的特征向量組成的信號子空間和噪聲子空間。

陣元域MUSIC 方位譜函數為

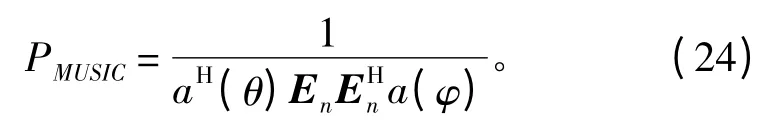
其中φ ∈Θ，Θ 表示觀察扇面。

讓φ 在觀察扇面Θ 內掃描，計算出式(24)在各掃描方位對應的函數值，該函數出現峰值的方位，即為信號方位估計值。3 個亮點的回波對魚雷來說相當于3 個信號源，根據窄帶陣元域MUSIC 方位估計原理，對潛艇目標亮點進行方位估計，從而實現對潛艇目標的識別。

3 仿真結果及分析

3.1 計算機仿真

假設魚雷自導系統發出的信號為梯形脈沖信號，仿真計算潛艇目標3 個亮點的回波信號的方位譜。仿真條件如下:魚雷發射信號載波頻率為30 kHz，采樣頻率為200 kHz。魚雷到潛艇的距離為500 m，艦橋和艦尾到艦首的距離L1和L2分別為75 m 和125 m，潛艇速度為5 m/s，聲速1 500 m/s。接收基陣為半波長間隔均勻線列陣，陣元個數M=10，混響為主要背景干擾，單位面積散射體的個數ρ=1。

自身多普勒抑制所用的濾波器的頻率響應如圖2所示，混響抑制效果如圖3所示。

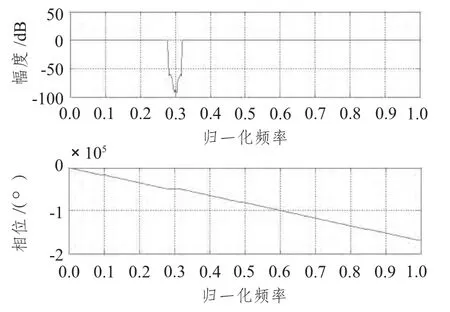
圖2 濾波器的頻率響應Fig.2 The frequency response of the filter

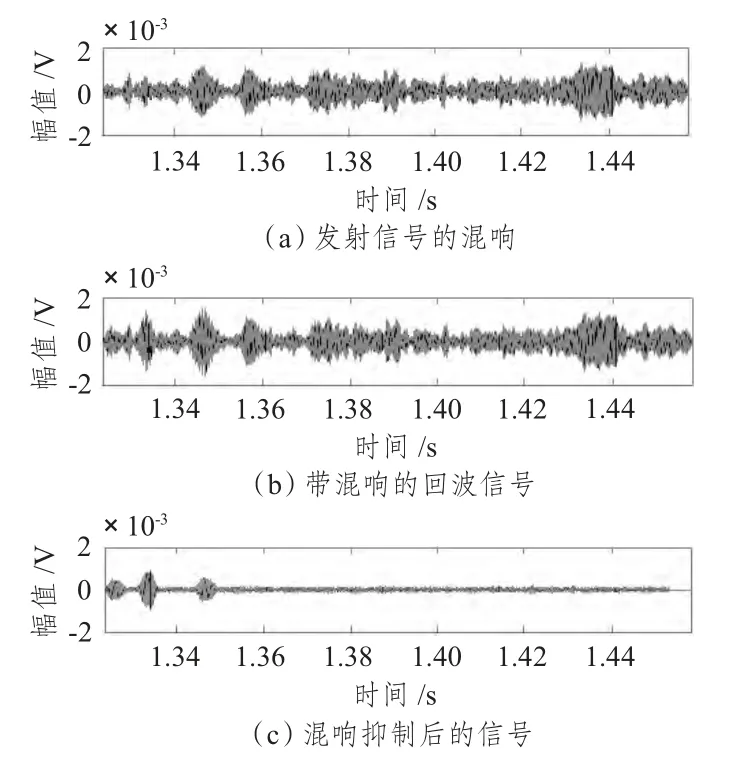
圖3 混響抑制效果Fig.3 Effect of reverberation suppression

把混響抑制后的回波信號，用MUSIC 算法進行目標亮點的方位估計。取不同的照射角θ 進行仿真，仿真結果如圖4 ～圖7所示。

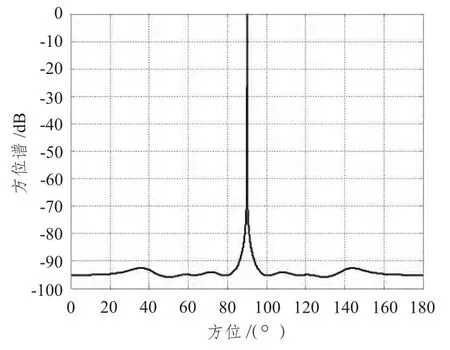
圖4 θ=0° 時方位譜Fig.4 The azimuth spectrum of θ=0°

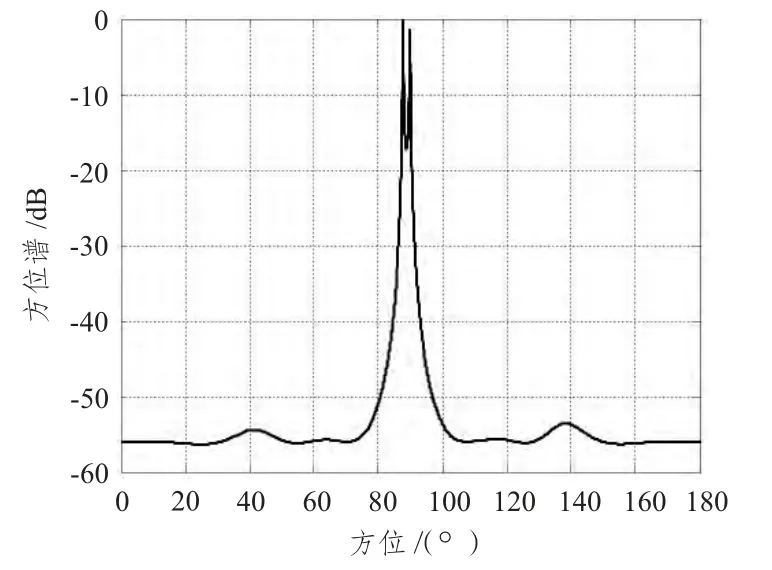
圖5 θ=10° 時方位譜Fig.5 The azimuth spectrum of θ=10°

3.2 結果分析

當魚雷相對潛艇的照射角θ 取不同值時，仿真產生的潛艇亮點回波的方位譜不同。圖4 是θ=0°時的方位譜，此時方位譜函數有1 個峰值，無法對3 個亮點進行識別。圖5 是θ=10°時的方位譜，此時方位譜函數有2 個峰值，只能對2 個亮點進行識別。圖6 是θ=20°時的方位譜，此時方位譜函數有3 個峰值，能夠對3 個亮點進行識別。圖7 是θ=90° 時的方位譜，此時魚雷位于潛艇的正橫方向，方位譜函數有3 個峰值，識別效果最好。這里只給出了θ ∈［0，90°］時典型角度的方位譜，當θ ∈(90°，180°］時，情況相似。

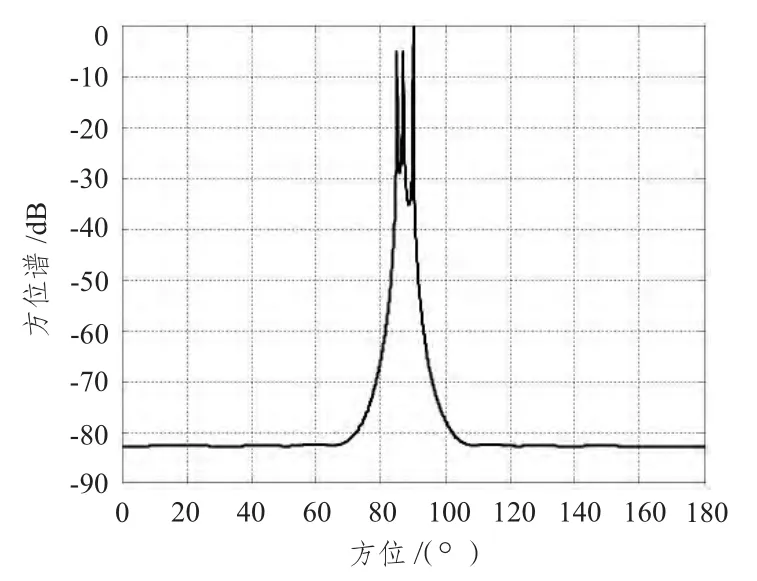
圖6 θ=20° 時方位譜Fig.6 The azimuth spectrum of θ=20°

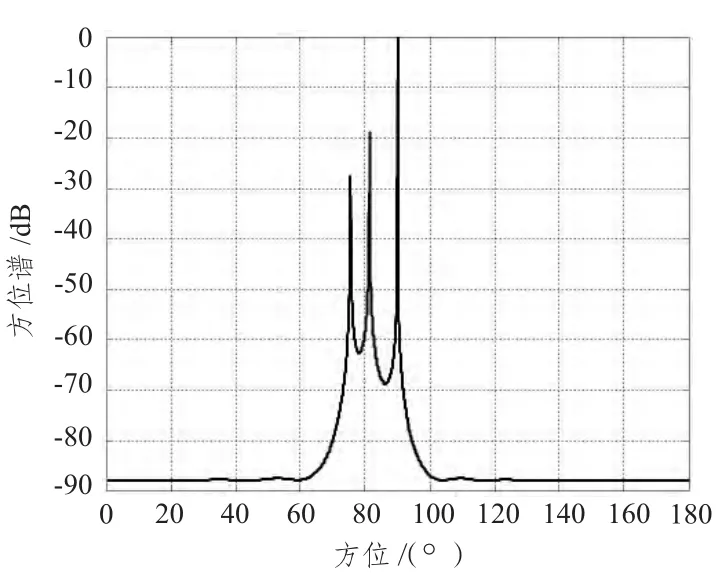
圖7 θ=90° 時方位譜Fig.7 The azimuth spectrum of θ=90°

本文只給出θ 取幾個典型值時的方位譜，在具體仿真中，θ 的取值間隔可以無限小。由仿真可以得出，當照射角θ∈［10°，170°］時，可以區分2 個亮點，能夠對潛艇尺度進行識別;當照射角θ ∈［20°，160°］時，可以區分3 個亮點，對潛艇目標的識別達到很好的效果;而在潛艇艦首和艦尾區即θ ∈［0°，10°)和θ ∈(170°，0°］時，不能對潛艇進行尺度識別。

4 結 語

在本文提出的潛艇目標尺度識別方法中，在建立混響條件下潛艇目標亮點模型的基礎上，用自身多普勒抑制技術對帶有混響的回波進行混響抑制，然后采用MUSIC 算法，對潛艇目標亮點的方位進行精確估計。仿真結果表明，該方法能夠很好地實現混響干擾下對潛艇目標的尺度識別，具有很高的理論價值和現實意義。

［1］劉伯勝，雷家煜.水聲學原理［M］.哈爾濱:哈爾濱工程大學出版社，1993.

［2］蘇紹璟，郭熙業，王躍科.一種海底混響時間序列仿真方法研究［J］.系統仿真學報，2010，88(8):1853-1861.

SU Shao-jing，GUO Xi-ye，WANG Yue-ke.A bottom reverberation time sequence simulation method research［J］.Journal of System Simulation，2010，88(8):1853-1861.

［3］陳文劍，孫輝，朱建軍，等.基于分數階傅里葉變換混響抑制的目標回波檢測方法［J］.聲學學報，2009.34(5):408-415.

［4］董陽澤，劉平香.聲自導魚雷反水聲對抗仿真研究［J］.系統仿真學報，2008，20(3):767-776.

［5］蔡平，梁國龍，葛鳳翔，等.界面混響信號的仿真研究［J］.哈爾濱工程大學學報，2000，21(4):31-35.

［6］湯渭霖.聲吶目標回波的亮點模型［J］.聲學學報，1994，9(2):92-100.

TANG Wei-lin.Sonar target echo highlight model［J］.Chinese Journal of Acoustics，1994，19(2):92-100.

［7］徐瑜，苑秉成，唐波.基于亮點模型的潛艇目標回聲過渡特性分析［J］.魚雷技術，2012，20(2):153-156.

［8］王明洲，黃曉文，郝重陽.基于聲學亮點特征的水下目標回波模型［J］.系統仿真學報，2003，15(1):21-25.

［9］何心怡，蔣興舟.淺?；祉懪c魚雷抗混響［J］.魚雷技術，2001，9(4):13-16.

HE Xin-yi，JIANG Xing-zhou.Reverberation in shallow sea and anti-reverberation for torpedo［J］.Torpedo Technology，2001，9(4):13-16.

［10］劉朝暉，馬國強.水下聲自導武器目標識別技術綜述［J］.聲學與電子工程，2004，75(3):25-30.

LIU Chao-hui，MA Guo-qiang.Underwater homing weapon target identification technology［J］.Acoustics and Electronics Engineering，2004，75(3):25-30.

［11］徐楓，嚴冰，王海陸，等.魚雷垂直目標亮點高分辨算法仿真與試驗研究［J］.魚雷技術，2009，17(6):35-40.

XU Feng，YAN Bing，WANG Hai-lu，et al.Torpedo vertical highlights high resolution algorithm simulation and test research［J］.Torpedo Technology，2009，17(6):35-40.