基于CFD的VIV剛性圓管縱橫比與雷諾數(shù)的作用效應(yīng)
劉楨兵
(中國船級(jí)社 舟山辦事處,浙江 舟山316000)
0 引 言
海洋天然氣和石油能源作為陸地能源的首要替代品,正日益受到全球科學(xué)界的重視,面對(duì)大規(guī)模的開采,首當(dāng)其沖的問題是克服流體介質(zhì)所帶來的影響。作為一種圓管結(jié)構(gòu),面對(duì)復(fù)雜海況,其所受載荷的狀況以及附近流場(chǎng)的分布備受關(guān)注。圓管在洋流作用下會(huì)產(chǎn)生渦激振動(dòng),并在流動(dòng)方向的2 個(gè)切點(diǎn)呈現(xiàn)周期性分離,最后在圓管的背流面產(chǎn)生渦的脫落,形成渦街現(xiàn)象[1]。以往的研究往往是針對(duì)二維模型進(jìn)行數(shù)值模擬,早期的Koopman 在低雷諾數(shù)下發(fā)現(xiàn)了渦脫落頻率與振動(dòng)頻率的吻合條件[2],隨后的 Ayoub &Karamcheti[3]針對(duì)三維流場(chǎng)提出了許多研究性和工程實(shí)際應(yīng)用上的寶貴結(jié)論,豐富的實(shí)驗(yàn)數(shù)據(jù)極大地帶動(dòng)了這一領(lǐng)域的發(fā)展。為了更好地觀察兩端固定于剛性壁端的圓管方向各個(gè)切面的流場(chǎng)信息,本文采用三維模型進(jìn)行分析,因此引入了圓管長度/圓管半徑縱橫比Aspect Ratio 這個(gè)概念,即AR=L/D,二維模型所模擬的效果反映的是AR 趨向無限值。本文使用AR 均為模擬長度與直徑具有可比性的情形。作者根據(jù)有限體積法,利用Fluent,Gambit,Matlab 以及Tecplot 等軟件對(duì)多種模型和流場(chǎng)情形進(jìn)行數(shù)值模擬,并得出最終結(jié)論。
1 模型構(gòu)建以及方法論
1.1 計(jì)算模型
圖1 為模擬的三維流場(chǎng)圖,表1 對(duì)流場(chǎng)圖的邊界和介質(zhì)進(jìn)行說明和闡述,表2 為Gambit 網(wǎng)格劃分后和優(yōu)化后的網(wǎng)格數(shù)目情況,經(jīng)過與實(shí)驗(yàn)數(shù)據(jù)及先前研究結(jié)果比對(duì)(見1.2 中無限AR 下的模擬結(jié)果)該模型模擬結(jié)果符合要求。其中周界尺寸如下:
X-方向:上游長度(左)=5D=5cm;下游長度(右)=25D=25cm。
Y-方向:流場(chǎng)寬度(前后)=5D=5cm。
Z-方向:流場(chǎng)深度(圓管長度)=4D/8D/10D=4cm/8cm/10cm。
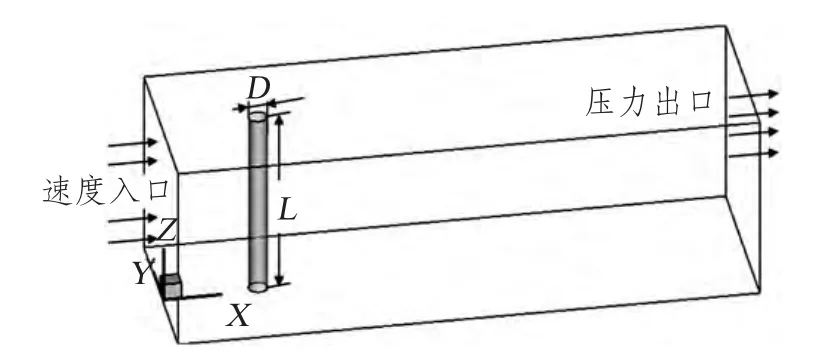
圖1 三維模型圖Fig.1 3D model
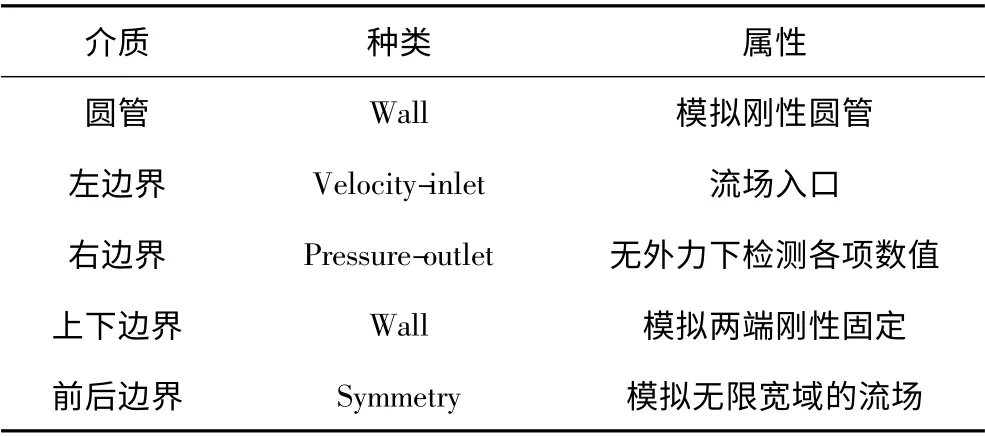
表1 邊界類型Tab.1 Boundary type
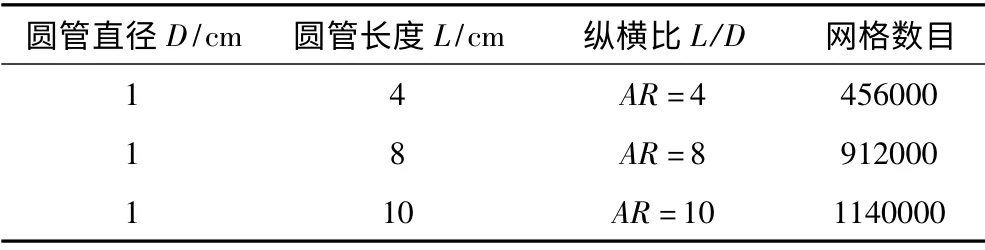
表2 不同縱橫比下三維模型網(wǎng)格數(shù)目Tab.2 Mesh number of 3D model under different aspect ratio

表3 不同雷諾數(shù)下對(duì)應(yīng)的流速Tab.3 Flow speed under different Reynolds number
1.2 數(shù)值計(jì)算方法
使用Fluent 12.1 對(duì)三維流場(chǎng)進(jìn)行模擬運(yùn)算,遵循納維-斯托克斯方程和連續(xù)方程這兩大守恒方程,針對(duì)Re 在300 以內(nèi)的情況均使用層流粘性模型
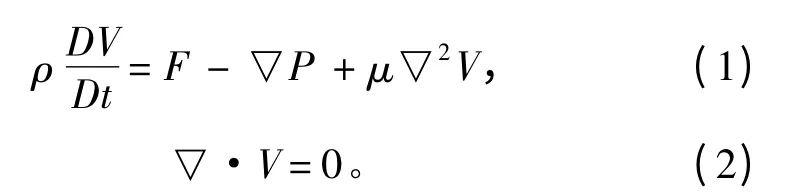
阻力系數(shù)和升力系數(shù)的數(shù)值取決于圓管表面粘性狀態(tài)以及作用力分布,根據(jù)以下公式計(jì)算所得
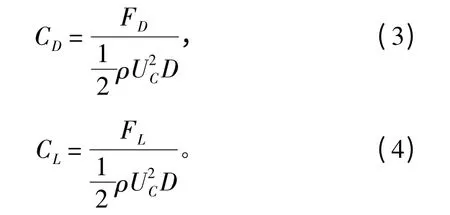
式中FD和FL為作用于圓管上的單位長度受力值,具體計(jì)算公式如下
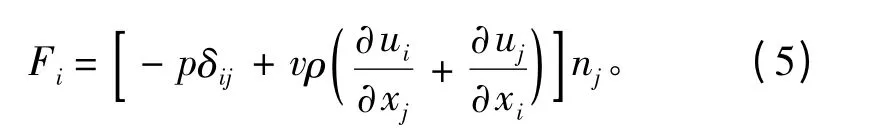
斯特羅哈數(shù)反映渦脫落現(xiàn)象,主要基于升力系數(shù)的主頻率

層流經(jīng)過圓管后的渦間距是圓管的伴流波長來定義的,根據(jù)式(7)計(jì)算所得

式中:U 為名義流速;fc為指渦脫落頻率;Cd,Cl 以及fc對(duì)應(yīng)的數(shù)值可在Fluent 中的FFT 功能獲取。
1.3 CFD 模型系數(shù)及參數(shù)設(shè)置
Versions:Fluent 12.1-3D
Solver:Pressure based
Formulation:Implicit
Time model:Unsteady
Unsteady formulation:2nd-order implicit
Viscous model:Laminar & Large Eddy Simulation
Pressure-Velocity Coupling:SIMPLE
Discretization of Pressure:Standard
Discretization of Momentum:2nd-oder upwind
Residual Absolute Criteria:1.0e-3
Reference Values:Area(L* D m* m),Density(1 024.73kg/m3),Length(D),Temperature(288.16K)velocity(Given in Tab.3)and viscosity(0.00 108 Ns/m2)
2 計(jì)算實(shí)例
2.1 模擬無限AR 下的流場(chǎng)
在Re=100 下的無限AR 三維數(shù)值模擬計(jì)算如圖2和圖3所示。經(jīng)過數(shù)值和渦街圖樣比較,與B.N.Rajani et al.[4],CHANG et al.[5]和BAI et al.[6]結(jié)果基本一致,因此可用于本文所用模型計(jì)算。

圖2 3D 切片示意圖Fig.2 3D-division slices
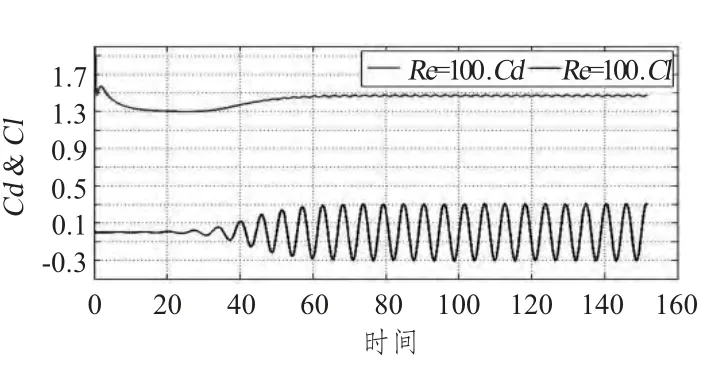
圖3 阻力系數(shù)和升力系數(shù)變化圖Fig.3 Time history curves of drag coefficients and lift coefficients
2.2 數(shù)值模擬計(jì)算
切面位置取3 處,分別為中部和端部1/8L(AR=4),1/16L(AR=8),1/20L(AR=10),切面圖如圖4 ~圖6所示,頻率分布與關(guān)系曲線如圖7 ~圖9所示,阻力系數(shù)與升力系數(shù)的對(duì)比如圖10所示,處理后數(shù)據(jù)結(jié)果如表4所示。

圖4 AR=4:不同Re 下切面圖(Ratio=4)Fig.4 AR=4:3D-division slices under different Reynolds number(Ratio=4)
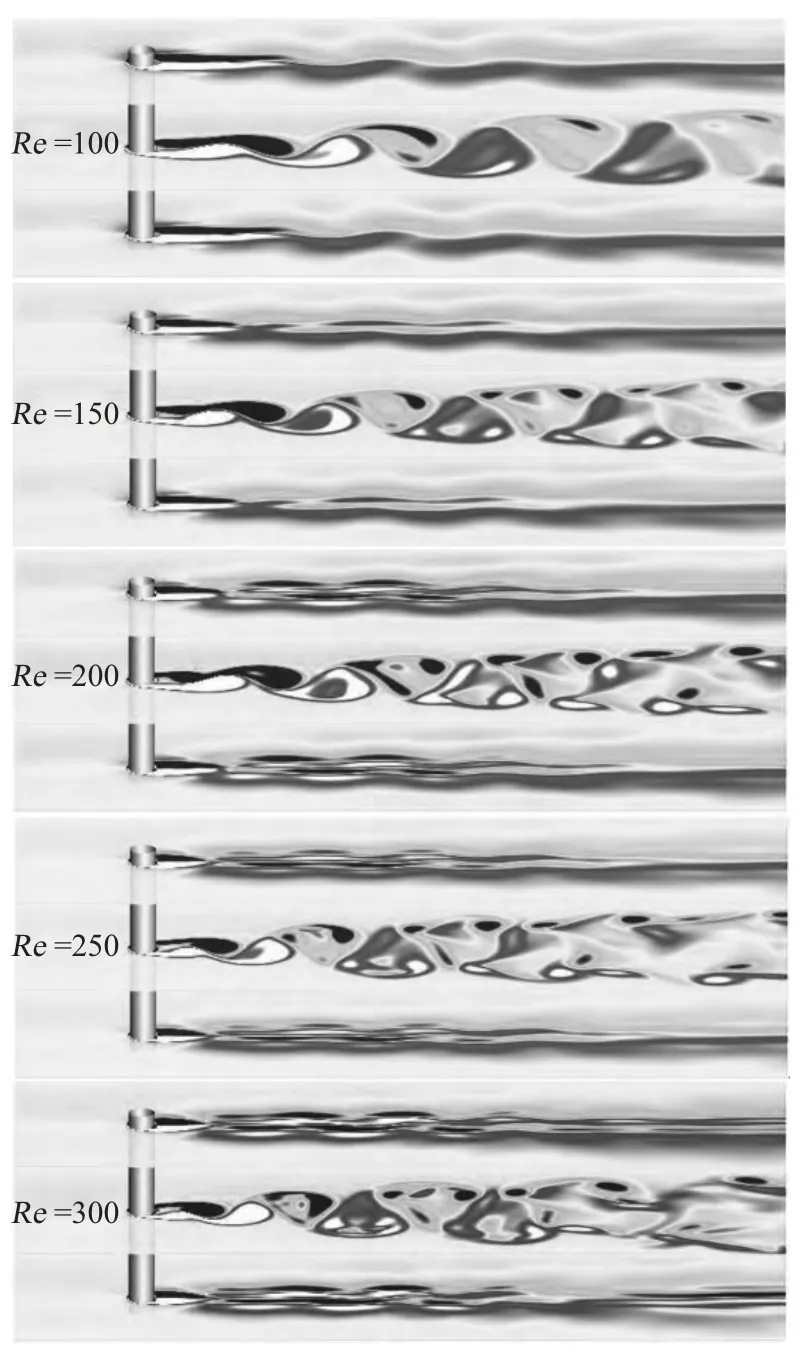
圖5 AR=8:不同Re 下切面圖(Ratio=8)Fig.5 AR=8:3D-Division slices under different Reynolds number(Ratio=8)
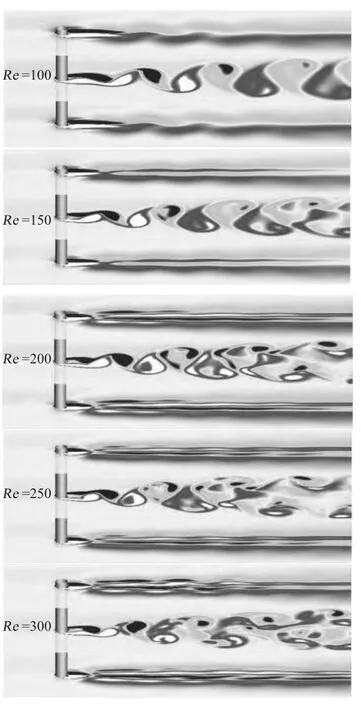
圖6 AR=10:不同Re 下切面圖(Ratio=10)Fig.6 AR=10:3D-Division slices under different Reynolds number(Ratio=10)
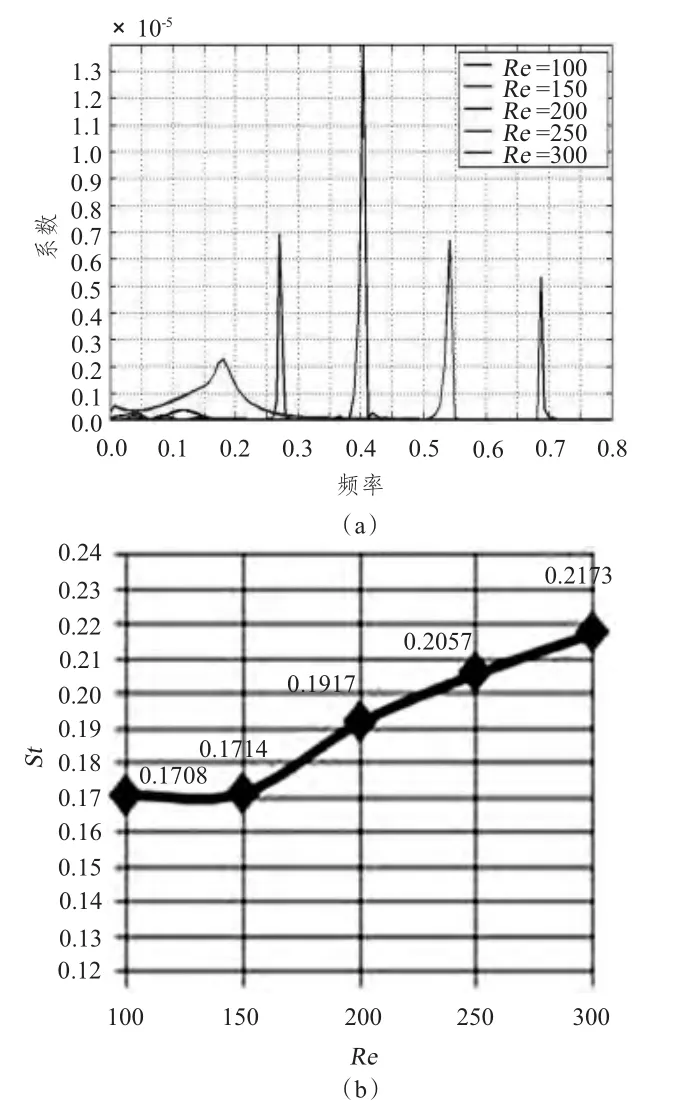
圖7 AR=4:渦脫落頻率分布圖及雷諾數(shù)-斯特羅哈數(shù)對(duì)應(yīng)關(guān)系圖Fig.7 AR=4:Vortex shedding frequency map and Re-St relational graph
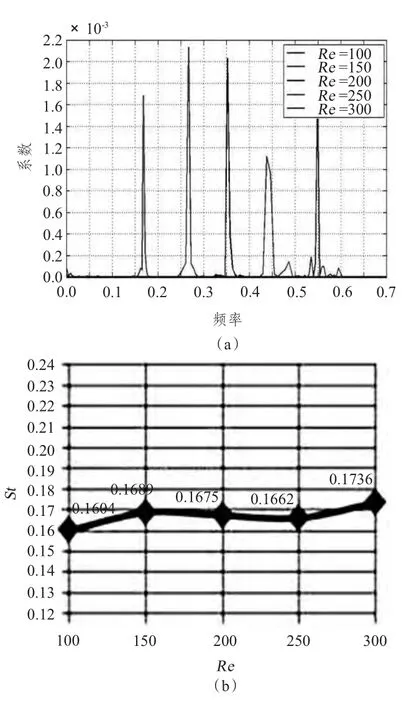
圖8 AR=8:渦脫落頻率分布圖及雷諾數(shù)-斯特羅哈數(shù)對(duì)應(yīng)關(guān)系圖Fig.8 AR=8:Vortex shedding frequency map and Re-St relational graph

圖9 AR=10:渦脫落頻率分布圖及雷諾數(shù)-斯特羅哈數(shù)對(duì)應(yīng)關(guān)系圖Fig.9 AR=10:Vortex shedding frequency map and Re-St relational graph
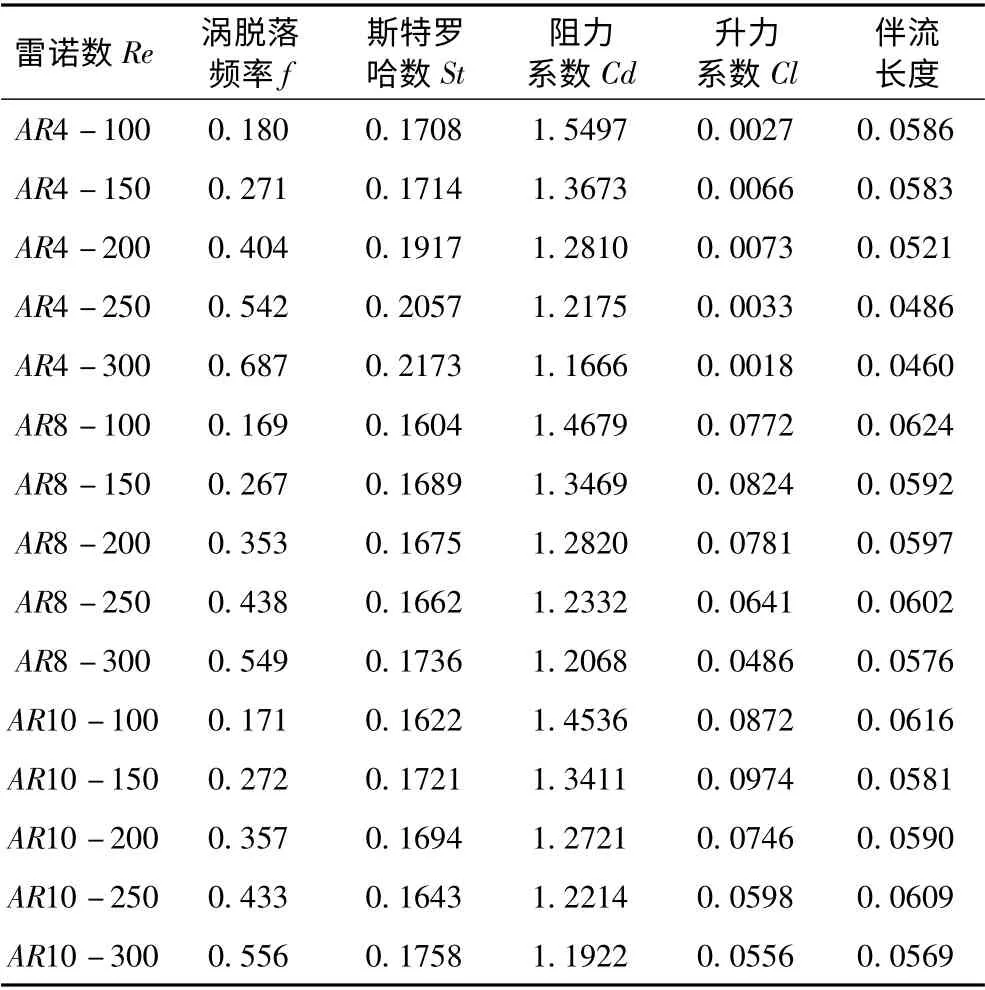
表4 Fluent 軟件綜合處理后數(shù)據(jù)結(jié)果Tab.4 Data & result analyzed by Fluent
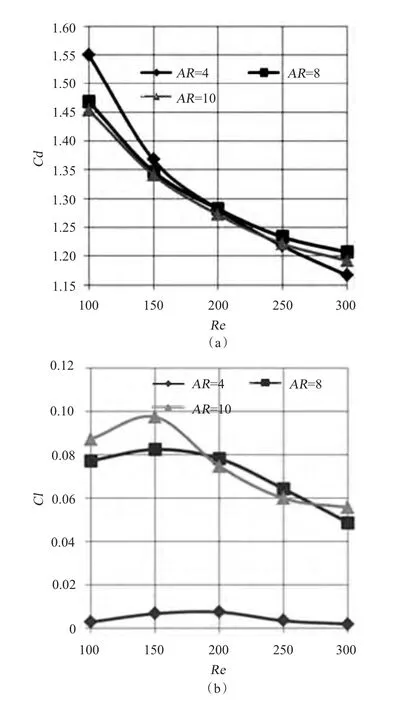
圖10 不同AR 與Re 下阻力系數(shù)和升力系數(shù)的對(duì)比圖Fig.10 Comparison diagram of drag coefficients and lift coefficients under different AR and Re
3 結(jié) 語
從上述數(shù)據(jù)圖中可以發(fā)現(xiàn),在相同縱橫比下,渦脫落的頻率隨著雷諾數(shù)的增加呈現(xiàn)遞增趨勢(shì),對(duì)以往的實(shí)驗(yàn)數(shù)據(jù)和模擬結(jié)果進(jìn)行佐證。在相同雷諾數(shù)下,小的縱橫比具有更大的渦脫落頻率,渦的變化形態(tài)更為復(fù)雜。阻力系數(shù)隨著雷諾數(shù)的增加呈現(xiàn)遞減趨勢(shì),在低縱橫比工況下尤為明顯,相同雷諾數(shù)下,以Re=200 為分界點(diǎn),隨縱橫比增加由遞減轉(zhuǎn)而遞增。升力系數(shù)隨雷諾數(shù)也呈現(xiàn)相同的遞減趨勢(shì),僅在雷諾數(shù)小于200 區(qū)域內(nèi)出現(xiàn)不穩(wěn)定過渡狀況,隨著雷諾數(shù)增加至200 后,變化趨勢(shì)趨于明顯,相同雷諾數(shù)下,縱橫比與升力系數(shù)成正比。由此發(fā)現(xiàn),層流模式下,流場(chǎng)基本屬于穩(wěn)定形態(tài),唯獨(dú)Re=200 是一個(gè)特殊臨界值,而伴流長度也在該處產(chǎn)生趨勢(shì)變化,這也是為何以往研究往往會(huì)涉及這一特殊工況,在無限AR 工況下,該雷諾數(shù)下的渦街極為明顯,而當(dāng)縱橫比被限定后,往往會(huì)有不可預(yù)見的變化產(chǎn)生,值得發(fā)掘并利用,對(duì)于近海開采以及SPAR 平臺(tái)的油氣開采具有指導(dǎo)意義。在今后的發(fā)展中,對(duì)洋流多自由度激勵(lì)工況以及圓管的柔性運(yùn)動(dòng)要加以研究,以獲得更好的工程應(yīng)用經(jīng)驗(yàn)。
[1]ARVIND S K,SHANKAR K V V,VIGNESH S.Renewable energy from vortex induced vibrations in a slow moving fluid[C].International Conference on Environmental Engineering and Applications,2010.
[2]KOOPMAN G H.The vortex wakes of vibrating cylinders at low Reynolds numbers[J].J.Fluid Mech,1967,28:501-512.
[3]ALFRED A,KARAMCHETI K.An experiment on the flow past a finite circular cylinder at high subcritical and super critical Reynolds numbers[J].J.Fluid Mech.1982,118:1-26.
[4]RAJANI B N,KANDASAMY A,SEKHAR M.Numerical simulation of laminar flow past a circular cylinder[J].Applied Mathematical Modelling,2009,33:1228-1247.
[5]CHANG Shu-ping,WANG Yong-sheng,PANG Zhi-yang.Numerical simulation of flow around circular cylinder using SST DES model[J].Ship Science and Technology,2009,31(2):30-33.
[6]BAI Hua,LI Jia-wu,XIA Yong.Numerical simulation and control measures of flow around circular cylinders at low reynolds number[J].Journal of Architecture and Civil Engineering.2010,27(4).

