無線傳感器網絡中高效建立干擾模型的研究

向亦宏，朱燕民

(上海交通大學計算機科學與工程系，上海 200240)

1 概述

由于無線網絡中的節點是通過廣播信號來傳輸數據包的，位于節點附近的其他節點可以監聽到這些信號，因此如果有2 個相鄰節點同時進行數據傳輸，它們發出的信號就會互相干擾，造成數據包的丟失以及網絡吞吐量的降低。現今，無線傳感器網絡(Wireless Sensor Network，WSN)越來越多地被部署到醫療、災害管理等數據密集型業務中，這些業務經常因為無線通信信道繁忙而受到嚴重的干擾。對遭受干擾的節點的性能進行精準刻畫，對擁塞控制、速率分配、信道分配等無線協議的有效運作具有重要的意義。因此，在無線傳感網絡中準確而快速地對當前的干擾狀況進行建模變得極其重要。

本文分別提出集中式算法和分布式算法，對傳感器網絡中的節點建立PRR-SINR 模型，并在含有17 個TelosB 節點的WSN 中對2 種算法進行性能評估。

2 相關研究

目前，對無線網絡中的干擾進行建模的方法較多，如基于跳數的模型［1］、基于距離的模型［2］和基于協議的模型［3］。這些模型都基于一個簡單的假設:數據包的接收與干擾之間的關系是二元的。當符合某種條件時，數據包一定會被節點接收，反之則一定不會被節點接收。文獻［4-6］中的分析表明這些模型并不精確。

在文獻［5-7］中，一個被稱為物理模型或者PRRSINR 的模型被提出，并被用于MAC 協議的設計中。文獻［6］比較了PRR-SINR 模型和其他基于二元關系的模型，得出的結論是PRR-SINR 性能最優，利用PRR-SINR 模型可以有效提高鏈路調度和網絡拓撲控制的性能［6-9］。

文獻［9-11］通過實驗表明，不同時間、不同地點，節點所測得的PRR-SINR 模型是不同的，實驗結果如圖1 所示。其中，圖1(a)為同一個節點在不同時刻所測得的PRR-SINR 模型;圖1(b)為同一個節點在不同位置所測得的模型。因此，需要為無線傳感器網絡中的每一個節點都建立一個PRR-SINR 模型，并周期地更新該模型。

圖1 不同時刻、不同位置節點測得的PRR-SINR 模型

文獻［6］中采用隨機選取無線傳感器網絡中不同的鏈路的方法來測量PRR-SINR 模型。文獻［10］提出了一種被動式的測量PRR-SINR 模型的方法。它不需要節點主動發送測量包，而僅僅是記錄各個節點發送正常數據包的時間戳以及節點成功接收數據包時的時間戳。每個節點將所記錄的時間戳發送給一個中心節點，由該節點來為每個節點生成PRR-SINR模型。上述方法都需要測量很長時間才能獲取整個網絡的PRR-SINR 模型。為此，本文分別提出一個分布式算法和集中式算法，對WSN 中的節點建立PRR-SINR 模型。集中式算法通過一個中心節點控制節點收發測量包，使每個節點可以逐步地建立模型，分布式算法則依賴每個節點自主控制自己的收發包狀況進行建模。

3 系統模型與問題描述

3.1 系統模型

在無線傳輸中，信號干擾噪聲比(Signal to Interference and Noise Ratio，SINR)的定義如下:

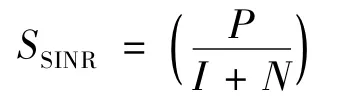
其中，P 為接收節點測量到的發送節點的發送功率;I代表的是接收節點測量到的干擾節點的發送功率;N是環境噪聲。PRR-SINR 模型可以用以下公式來描述:

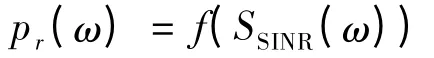
如圖1 所示，PRR-SINR 模型中存在一個過渡區域。過渡區域以外的包接收率為0 或者100%。而過渡區內的包接收率在0～100%之間。因此，只需要考慮如何刻畫過渡區域即可。因為大多數傳感器節點的RSSI(接收信號強度寄存器)能夠提供的RSS(接收信號強度)值的精度為1 dBm，所以信號與干擾的RSS 值的差值精度為1 dB，此差值即為所求SINR。文獻［6］經過實際測量，得出過渡區間在［0，5 dB］，因此，僅需要為每個節點測量6 個整數SINR 所對應的PRR 即可為該節點構建完整的PRR-SINR模型。

3.2 問題描述

本文的目標是使用最少的測量包來為WSN 中的每一個節點構建PRR-SINR 模型。基本方法如下:在WSN 中選取一些節點作為一個發送子集。這個子集中的每個節點從某個時刻開始需要同時以相同的間隔發送指定數目(M)的測量包。從發包開始到結束的這段時間稱為一個輪次。可以認為每個節點事先都已經測量了該節點接收其鄰居節點發出的數據包的RSS，并且這些RSS 在短期內不會變化。

例:圖2 中r1，r2，r3 組成了一個發送子集，其中，r2 是m 的鄰居節點，r1 和r3 是干擾節點，圖中虛線代表干擾鏈路。

圖2 PRR-SINR 點的測量

輪次開始后，這3 個節點同時發包。m 節點在此輪中處于監聽模式。它收到r2 發出的包時，從RSSI 中讀取接收此包的RSS(包含了背景噪聲，r1，r3 的干擾信號強度)。由于r2 是m 的鄰居節點，因此m 節點保存了在無干擾的情況下，接收r2 數據包的RSS。m 節點可以據此計算出接收此包的SINR:

如果得出的SINR 還沒有對應的PRR 值，那么m 在此輪中只統計接收到的r2 發出的數據包的個數。在該SINR 下，節點m 的包接收率公式為:

則稱在該發送子集下，m 獲取了一個PRR-SINR點。

通過上述步驟，可以逐步為網絡中的每一個節點構造PRR-SINR 模型。本文選擇K 個發送子集組成一個發送集合S。當一個發送子集形成的輪次結束后，節點m 可以獲取0 個或1 個PRR-SINR 點。令fs(nodem)≥N 代表發送集合S 中的發送子集都發完測量包后，節點m 總共可以計算出的PRR-SINR點的個數。每個節點需要在過渡區域中獲取至少N 個PRR-SINR 點，即需要滿足以下條件:

因為一個發送子集中的每個節點都需要發送M 個測量包，所以為了達到使用最少測量包的目標，筆者希望選擇K 個發送子集，這些子集含有的節點的數目的和是最少的。本文問題描述如下:

3.3 復雜度分析

引理1 選擇集問題是NP 的。

證明:NP 類由這樣的問題∏組成，對于這些問題存在一個確定性算法A，該算法在對∏的一個實例展示一個斷言解時，它能在多項式時間內驗證解的正確性［12］。

在本文的選擇集問題中，如果給定一個發送集合S={s1，s2，…，sk}，則需要驗證是否有:

引理2 集合覆蓋問題可以歸約到選擇集問題。

證明:給定集合W={w1，w2，…，wm}和V={v1，v2，…，vt}，vi為W 的子集。集合覆蓋問題可以描述為:

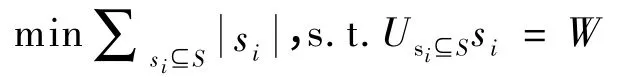
其中，S 為V 的一個子集，si為S 中的元素，為si的權重。集合覆蓋問題即要求從V 中找到一個子集，這些子集中元素的并集包含了W 中的每個元素，并且子集中元素的權重的和最小。

在本文的選擇集問題中，如果一個發送子集si可以使節點i 獲取一個PRR-SINR 點，則稱si覆蓋了節點i。si的權重為si中發送節點的個數。令N=1，如果S*={s1，s2，…，sk}是本文選擇集問題的解，也就是說找到了一個集合S*，它滿足每個節點都被覆蓋一次的條件。顯然，這個解也就是集合覆蓋的解。也即當且僅當S*為選擇集問題的解時，S*為集合覆蓋的解。因此，可以把集合覆蓋問題歸約到選擇集問題。

定理 選擇集問題是一個NP 完全問題。

證明:由引理1 和引理2 可以得出，選擇集問題是一個NP 完全問題。

4 集中式算法

在集中式算法中，要求網絡中每個節點都需要事先測量收到鄰居節點數據包時的RSS，然后將這些數據發送給一個中心節點。中心節點使用這些數據模擬出一個發送子集，測試那些不在發送子集中的節點能否通過此發送子集獲取一個PRR-SINR點，進而計算出建立整個網絡的PRR-SINR 模型所需要的發送子集的集合。中心節點完成計算后，在每一個輪次開始之前告訴其他節點在該輪如何表現，例如直接加入發送子集充當發送者，或者只是統計收到某個節點發出的數據包的個數，從而構建某個PRR-SINR 點。

由于選擇集問題是一個NP 完全問題，因此本文提出一個貪心隨機算法，該算法部署在中心節點上，能在多項式時間內提供一個近似解。算法的具體步驟如下:

(1)發送子集集合S={}。

(2)發送子集si清空。

(3)隨機從網絡中選擇一個節點加入到發送子集si，將Xmax設置為0。

(4)遍歷所有不在發送子集中的節點，測試將該節點i 臨時加入到發送子集后，能獲取PRR-SINR 點的節點的個數X。

(5)選擇步驟(4)中最大的X 以及對應的節點i，如果X 大于Xmax，那么將節點i 正式加入發送子集si，將Xmax設置為X，繼續4)。如果Xmax為0 的次數超過了一個閾值，則跳轉到步驟(7)。

(6)如果Xmax大于0，將該發送子集si加入S，判斷每個節點是否都已經建立了PRR-SINR 模型，如果仍沒有建立，則繼續執行步驟(2)。

(7)結束。

5 分布式算法

在集中式算法中，由一個中心節點來決定網絡中的節點是否加入發送子集中。而在本文提出的分布式算中，每個節點需要自己來判斷是否成為發送子集中的一員。只有當發送子集形成后，其他節點才能獲知自己能否通過此子集來得到一個未使用過的SINR 點。因此，節點不能預知自己做出的決策是如何影響其他節點的。本文通過一個啟發式的方法來幫助節點判斷自己是否加入發送子集。

如3.1 節所述，需要為每個節點測量6 個SINR所對應的PRR。本文根據這個事實來給每個節點提供決策依據:當節點得知它的鄰居還需要計算的PRR-SINR 點數的平均值大于本節點剩余PRR-SINR點數時，節點以概率P1(大于0.5)加入發送子集，否則節點以概率P2(小于0.5)加入。這樣，可以讓那些還需測量更多PRR-SINR 點數的節點優先充當接收者，從而盡可能地測量出更多的PRR-SINR 點。為了讓節點更有效地參與建模，定義另一個規則:如果某個節點在一輪結束后發現它的鄰居節點的PRR-SINR 點數與上一輪是一樣的，那么認為該節點在此輪中的表現是無價值的，需要對該節點進行懲罰，即如果該節點在此輪中是發送者，那么在下一輪中，需要降低該節點充當發送者的概率;同樣的，如果該節點在此輪中是接收者，那么在下一輪中該節點將更有可能充當發送者。

實驗結果表明，上述規則可使發送節點的數目減少約33%。本文將發送輪次限制為N，力圖保證模型精度的前提下，使用盡可能少的節點發送測量包。

分布式算法部署在網絡中的每個節點上，算法的具體步驟如下:

(1)節點以概率P 確定自己是否加入發送子集充當發送者，充當發送者的話，節點開始以固定頻率發送測試包。發送完指定數目的測試包后，轉入步驟(3)。

(2)節點i 充當接收者，處于監聽模式。當成功收到節點K 發送的測試包時，計算此時的SINR，如果該SINR 沒有對應的PRR，則接下來節點i 只統計收到K 發送的包的個數，計算PRR。

(3)各個節點對外廣播自己還剩余的PRR-SINR點數。其余節點更新鄰居還剩PRR-SINR 點數。據此計算出節點在下一個輪次充當發送者的概率。

(4)如果已進行的輪次數目沒有達到N，則繼續步驟(1)。

(5)結束。

6 性能評估

本文實驗平臺由17 個運行TinyOS-2.02 系統的TelosB 節點構成，一個節點充當中心節點，其余16 個節點均勻分布在4 m ×4 m 的空間上。上文所述的集中式算法和分布式算法均在此平臺上進行性能評估。

6.1 精度評估

本文采用文獻［5-7］中使用的一種主動干擾測量方法(簡稱ACTIVE 方法)來與本文提出的方法進行比較。該方法通過m 輪的測量，為一個節點構造生成一個PRR-SINR 模型。當要為節點m 生成模型時，先為m 節點選取一些輔助節點，這些輔助節點負責在每一輪中以相同的時間間隔廣播數據包。m 節點事先知道接收這些節點發出的數據包的RSS。這樣，m 節點在每一輪選取一個輔助節點r，計算此時的SINR 以及接收到的r 發出的包的個數。通過改變輔助節點的發送功率，m 節點可以計算出不同的SINR，從而生成一個完整的PRRSINR 模型。文獻［5-7］的實驗結果表明，如果輪次足夠多，則上述方法建立的PRR-SINR 模型可達到較高的準確率。

本文以4 096 輪次的ACTIVE 方法所構建的PRR-SINR 模型為基準，評估本文提出的方法的精確性。實驗的具體步驟如下:

(1)使用集中式算法測得整個網絡的PRR-SINR模型。

(2)使用分布式算法再次為每個節點構造PRR-SINR模型，重復多次。

(3)通過ACTIVE 方法為每個節點生成PRRSINR 模型。

(4)將集中式算法和分布式算法為每個節點所計算的模型與ACTIVE 生成的相比較，計算出節點過渡區域中每個SINR 對應的PRR 與ACTIVE 相比的絕對誤差值。

2 種算法為每個節點生成模型的平均誤差累計分布函數(Cumulative Distribution Function，CDF)圖如圖3 所示。其中，分布式算法輪次分別限制為30 輪和100 輪。可以看出，集中式算法得到的PRR-SINR模型精度較高，最大平均誤差為5.7%，中值只有4.6%。30 輪的分布式算法所得模型最大平均誤差9.4%，中值為7.0%。100 輪的分布式算法精度有一定提升，最大平均誤差6.5%，中值降到4.5%。

圖3 2 種算法所得模型的平均誤差CDF 圖

6.2 開銷評估

本文用實驗中收集的數據在PC 上窮舉所有可能的發送子集集合，從滿足條件的集合中，找出最少的發送者數目，然后將之與集中式算法和30 輪分布式算法進行比較，結果如圖4 所示。可以看出，集中式算法平均所需的發送者個數與最優解很接近，其最差的表現也不超過最優解的2 倍。分布式算法平均只需要2 倍于最優解的發送者，最差時也只需要4 倍的發送節點。

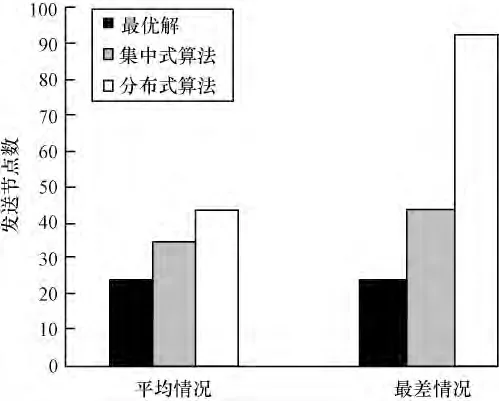
圖4 2 種算法所需發送節點數與最優解的比較

在集中式算法和分布式算法中，發送節點每10 ms發送一個測量包，每輪一共發送100 個，每輪耗時1 s。實驗中，集中式算法平均需要14 輪，最多16 輪來完成網絡模型的建立，即集中式算法需要平均耗時14 s，最差時耗時16 s 來建立模型。分布式算法指定使用30 輪來進行測量，因此耗時30 s 構建網絡模型。從對文獻［10］方法的實驗結果看，為達到中值平均誤差7%，其需要耗時2.5 min。因此，可以看出，本文提出的2 種算法在時間開銷上性能較好。

7 結束語

隨著無線傳感器網絡越來越多的被部署到醫療、災害管理等各項數據密集型業務之中，網絡中節點信息傳輸的干擾也越來越受到重視，如何高效地為節點建立干擾模型成為研究熱點。本文提出了2 種高效建立PRR-SINR 干擾模型的方法，一種是集中式的，另一種是分布式的，分別用于不同的場景。從實驗的結果可以看出，2 種算法都具有較高的精度，而且建立模型所需時間較短，額外的開銷較少。下一步工作將對分布式算法進行優化，在提高其精度的同時，進一步減少所需發送節點的數目。

［1］Sharma G，Mazumdar R，Shroff N.On the Complexity of Scheduling in Wireless Networks［C］//Proceedings of MobiCom'06.Los Angeles，USA:ACM Press，2006:227-238.

［2］Alicherry M，Bhatia R，Li L E.Joint Channel Assignment and Routing for Throughput Optimization in Multi-radio Wireless Mesh Networks［C］//Proceedings of MobiCom'05.Cologne，Germany:ACM Press，2005:58-72.

［3］Gupta P，Kumar P R.The Capacity of Wireless Networks［J］.IEEE Transactions on Information Theory，2000，46(2):388-404.

［4］Zhao J，Govindan R.Understanding Packet Delivery Performance in Dense Wireless Sensor Networks［C］//Proceedings of SenSys'03.Los Angeles，USA:ACM Press，2003:1-13.

［5］Son D，Krishnamachari B，Heidemann J.Experimental Study of Concurrent Transmission in Wireless Sensor Networks［C］//Proceedings of SenSys'06.Boulder，USA:ACM Press，2006:237-250.

［6］Maheshwari R，Jain S，Das S R.A Measurement Study of Interference Modeling and Scheduling in Low-power Wireless Networks［C］//Proceedings of SenSys'08.Raleigh，USA:ACM Press，2008:141-154.

［7］Sha Mo，Xing Guoliang，Zhou Gang，et al.C-mac:Model-driven Concurrent Medium Access Control for Wireless Sensor Networks ［C］//Proceedings of INFOCOM'09.Rio de Janeiro，Brazil:IEEE Press，2009:1845-1853.

［8］Brar G.Blough D M，Santi P.Computationally Efficient Scheduling with the Physical Interference Model for Throughput Improvement in Wireless Mesh Networks［C］//Proceedings of MobiCom'06.Los Angeles，USA:ACM Press，2006:2-13.

［9］Rangwala S，Gummadi R，Govindan R，et al.Interference Aware Fair Rate Control in Wireless Sensor Networks［C］//Proceedings of SIGCOMM'06.Pisa，Italy:ACM Press，2006:62-74.

［10］Liu Shucheng，Xing Guoliang，Zhang Hongwei，et al.Passive Interference Measurement in Wireless Sensor Networks［C］//Proceedings of ICNP'10.Kyoto，Japan:IEEE Press，2010:52-61.

［11］Huang J，Liu S，Xing G，et al.Accuracy-aware Interference Modeling and Measurement in Wireless Sensor Networks［C］//Proceedings of ICDCS'11.Minneapolis，USA:IEEE Press，2011:172-181.

［12］Alsuwaiyel M H.算法設計技巧與分析［M］.吳偉昶，方世昌，譯.北京:電子工業出版社，2010.