基于云模型的入侵雜草優化算法

劉 挺,王聯國

(甘肅農業大學信息科學技術學院,蘭州730070)

1 概述

雜草具有生命力旺盛、繁殖力強、傳播途徑多樣等特性,長久以來對農作物的生長構成了嚴重的威脅。根據雜草的特點,文獻[1]提出了一種入侵雜草優化(Invasive Weed Optimization,IWO)算法。如今,IWO 已經被成功應用于DNA 編碼排序[2]、電力優化調度[3]、無線電配置[4]以及圖像聚類[5]等眾多領域。盡管如此,雜草算法也存在著求解精度低、易陷入局部值等缺點[6]。針對這些問題,眾多學者采取了各種不同的策略致力于提高IWO 的性能[7-8]。

云模型的概念是由李德毅于1995 年提出的[9]。云模型把隨機性和模糊性結合起來,用數字特征熵,揭示隨機性與模糊性的關聯性,實現了定性與定量之間轉換的過程。本文提出了一種云自適應雜草優化(Cloud Adaptive IWO,CLIWO)算法,根據雜草的適應度值大小進行分群操作,并根據云理論和每個群的實際情況自適應選擇調整因子[10]。

2 基本雜草優化算法

基本IWO 算法對雜草的生長繁殖過程進行了模擬,主要分為種群初始化、產生種子、空間擴散以及競爭排斥4 個過程,具體的操作步驟如下：

步驟1種群初始化

初始化種群起始位置,初始化種群數目Popsize、最大種群數Pmax,規定搜索空間大小、空間維數、最大最小種子生成數,最大迭代次數、初始標準差、終止標準差以及非線性調和指數。

步驟2產生種子

生成種子的數目是根據父代雜草適應度值大小比例而定的,每個雜草所產生的種子數目為：

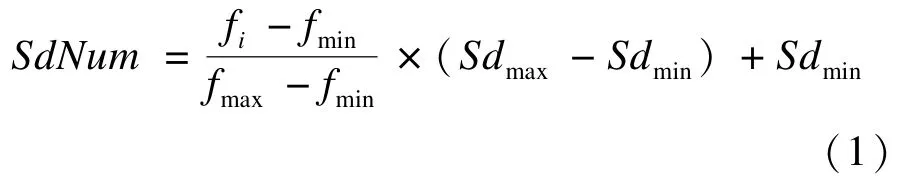
其中,fi代表第i個雜草的適應度值；SdNum為父代雜草生成種子的數目；fmax,fmin分別為種群當前最大與最小的適應度值；Sdmax,Sdmin分別為個體能生成的最大、最小種子數目。

步驟3空間擴散

生成的種子以正態分布的形式擴散在父代雜草個體周圍,具體實現按照式(2)所示。

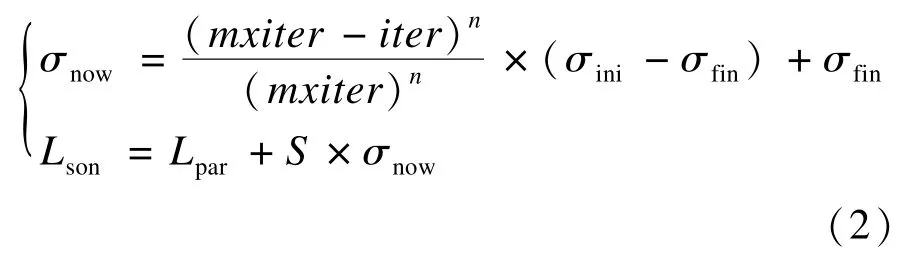
其中,σnow為當前的標準差；σini,σfin分別為初始、終止標準差；iter為當前的迭代次數；mxiter為最大迭代次數；n一般取3 為非線性調和指數；Lson表示產生的種子位置；Lpar代表父代雜草位置；S為正態分布函數。

根據式(2)可以看出,算法初期,由于迭代次數較小,當前標準差較大,S和σnow的乘積也相對較大,算法搜索的范圍也較大,因此算法這時處于全局搜索階段；隨著搜索的進行以及迭代次數的不斷增加,當前標準差會隨之減小,S與σnow的乘積也會隨之減小,搜索的范圍也在減小,這時搜索過程則變得更加精細。

步驟4競爭排斥

算法經過擴散后種群數量會達到一個最大值Pmax,將種子和父代雜草個體一并按照適應度值大小進行排序,選取適應度值較好的前Pmax個個體進入下一次迭代。

3 云模型

定義設X是一個普通集合,X={x},稱為論域,關于論域X中的模糊集合A,是指對于任意元素x都存在一個有穩定傾向的隨機數uA(x),叫做x對A的隸屬。如果論域中的元素是簡單有序的,則X可以看作是基礎變量,隸屬度在X上的分布叫做隸屬云；如果論域中的元素不是簡單有序的,而根據某個法則f,可將X映射到另一個有序的論域X’上,X’中的一個且只有一個x’和x對應,則X’為基礎變量,隸屬度在X’上的分布叫做隸屬云。

若隸屬度在X上的分布滿足正態分布叫做正態云模型,正態云是一個具有穩定傾向的隨機數組成的集合,用期望Ex,熵En,超熵He這3 個概念表示。

X條件云發生器[11]：X條件云發生器是根據期望Ex,熵En,超熵He這3 個特征值,在X上產生的滿足正態隸屬云分布規律的云滴σ(x0,u),這種發生器裝置叫做X條件云發生器。

輸入{Ex En He},n,x0

輸出{(x0,u1),(x0,u2),…,(x0,un)}

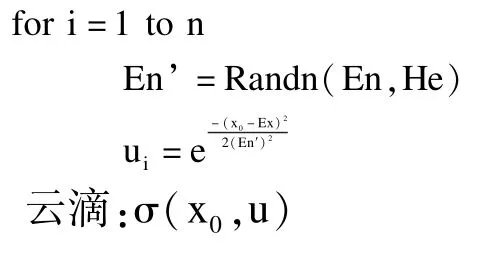
4 云自適應雜草優化算法

4.1 自適應分群策略

設雜草種群大小為N,種群中每個雜草個體對應的適應度為fi,將種群中所有雜草個體求平均適應度得種群最優雜草個體的適應度值為fmin；對于適應度值優于fmean的個體,將它們的適應度求平均值得到f′mean；對于適應度值次于fmean的個體,將它們的適應度求平均值得到f″mean。本文算法將雜草的擴散公式按式(3)調整。

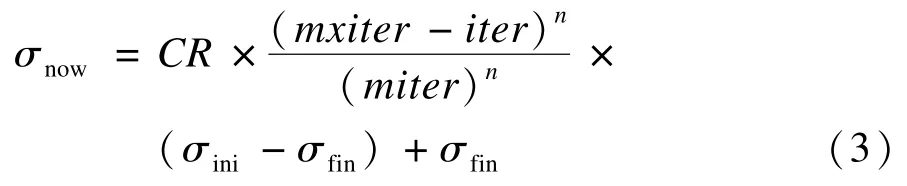
其中,CR∈[0,1]為調整因子[12]。

在基本雜草算法中雜草每次擴散的步長是根據迭代次數增加而非線性減小的,這種擴散方式在每代中σnow是一個不變的常數,這樣如果σnow過大或者過小很有可能使搜索跳過或者未能到達最優個體,這樣就導致了搜索能力的下降。針對這種情況,將雜草分為3 個子群,根據不同子群的情況采取不同的調整因子生成策略,具體分群策略如下：

(1) 優良子群：fi優于f′mean

該子群中的雜草個體屬于種群中的優秀個體,其距離全局最優個體比較近,因此,采用較小的調整因子CR,達到精細搜索的目的。CR的取值為0.2。

(2) 普通子群：fi優于f″mean但差于f′mean

該種群中的個體為質量一般的部分,也是相對其他2 個種群雜草個體數量最多的種群。該種群的調整因子使用X條件云發生器產生,對種群進行動態的調整,具體產生過程如下：

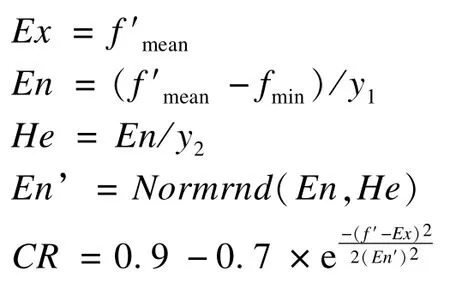
(3) 較差子群：fi次于f′mean”

該種群中的個體屬于質量較差的個體,相對最優個體距離較遠,因此,采用較大的調整因子,增加搜索的范圍,有助于更加迅速地找到最優解。這里CR 的取值為0.9。

4.2 算法流程

CLIWO 算法流程如下：

步驟1在D維空間中初始化種群大小N,確定Popsize,Pmax,σini,σfin,Sdmax,Sdmin以及mxiter等相關參數。

步驟2判斷算法是否達到終止條件。若達到,輸出最優解；否則,執行步驟3。

步驟3計算種群中每個雜草個體的適應度值,并計算fmean,fmin,f′mean,f′mean’。

步驟4依照自適應分群策略將雜草分為3 個子群。

步驟5對于每個子群中的每個個體按照式(1)產生相應的種子。

步驟6針對每個子群的情況,根據式(3)將子代雜草進行擴散操作。

步驟7將3 個子群的父、子代雜草放在一起,并且按照適應度大小進行排序,選擇適應度較優的前Pmax個雜草,然后轉步驟2。

時間復雜度分析：

(1) 需要對N個雜草進行初始化,且每個個體是D維的,時間復雜度為O(N×D)。

(2) 判斷終止條件,時間復雜度為常數。

(3) 計算雜草適應度,并計算fmean等相關值,l,s,p(l+s+p=N)分別表示3 個不同子群的雜草個數數目,Tl,Ts,Tp分別表示3 個子群迭代需要的時間,由于Tl,Tp的時間為O(1),Ts的時間為O(s×D),時間復雜度為2O(1) +O(s×D)。

(4) 根據適應度分群,時間復雜度為O(N)。

(5) 種子產生,時間復雜度為O(N)。

(6) 種子擴散,時間復雜度為O(N)。

(7) 進行競爭排序機制,若產生種子個數為Ns,則最小時間復雜度為(N+Ns)(lb(N+Ns))。

與基本IWO 算法相比,CLIWO 需要將所有雜草個體分群之后,再對群成員進行繁殖、擴散操作,s是N中的個體,分群調整因子生成策略的時間復雜度2O(1) +O(s×D)不會高于O(N×D),不足以提高基本IWO 算法的復雜度數量級。

5 仿真實驗與結果分析

5.1 測試函數

為了檢驗CLIWO 的尋優性能,本文選取了7 個以最小值為基準的測試函數,并進行了仿真實驗。測試函數f1～f7均存在最小值,并且最小值為0。其中,f1～f4屬于單峰函數,f5～f7屬于多峰函數。具體函數參見表1。

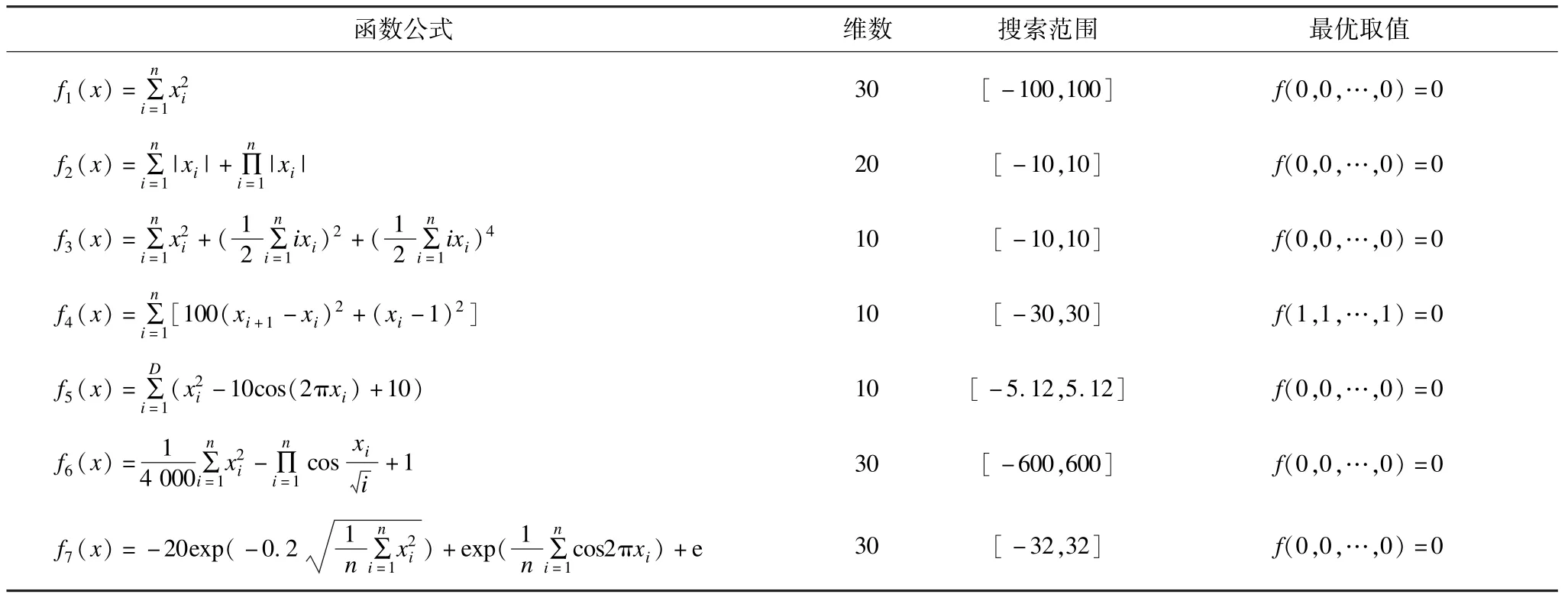
表1 測試函數

5.2 實驗參數設置

實驗中具體參數設置為：種群規模為15 株雜草,雜草的最大生成數目為30 株,算法的最大迭代次數為200,非線性調和指數n為3；在此基礎上,為了確定算法中另外3 個重要參數,對CLIWO 進行了如下的實驗：

(1) 在保持初始結束標準差以其他相關參數相同的情況下,固定種子的最小生成數目為0,使種子的最大生成數Sdmax取不同值并且經過了多次實驗,結果選取最佳的Sdmax。

(2) 由于算法的初始標準差過大會導致搜索的實際步長超過搜索空間的范圍,因此在(1)的基礎上,固定最終標準差為0.01 以及其他實驗相關參數,在可行域內調整初始標準差σini并經過多次實驗,選取最佳的σini。

(3) 在(1)、(2)的基礎上,嘗試分別在[0,1]選取多個不同數值作為CR的取值,經過多次實驗,選取最佳的CR值。

受篇幅影響,只列出最終的實驗結果,種子的最大生成數Sdmax取15,初始標準差σini設為WD/3(WD為搜索的上界),CR的臨界值取為0.2 與0.9,算法尋優結果最佳。

5.3 實驗結果

用基本雜草優化算法(IWO)、文獻[13]中的算法(CMIWO)與本文算法(CLIWO),分別對以上7 個測試函數進行優化,測試的結果取獨立運行50 次后得到的平均值。實驗結果如表2 所示。圖1描述了上述3 種算法對函數f1～f7經歷200 次迭代的適應度進化曲線。

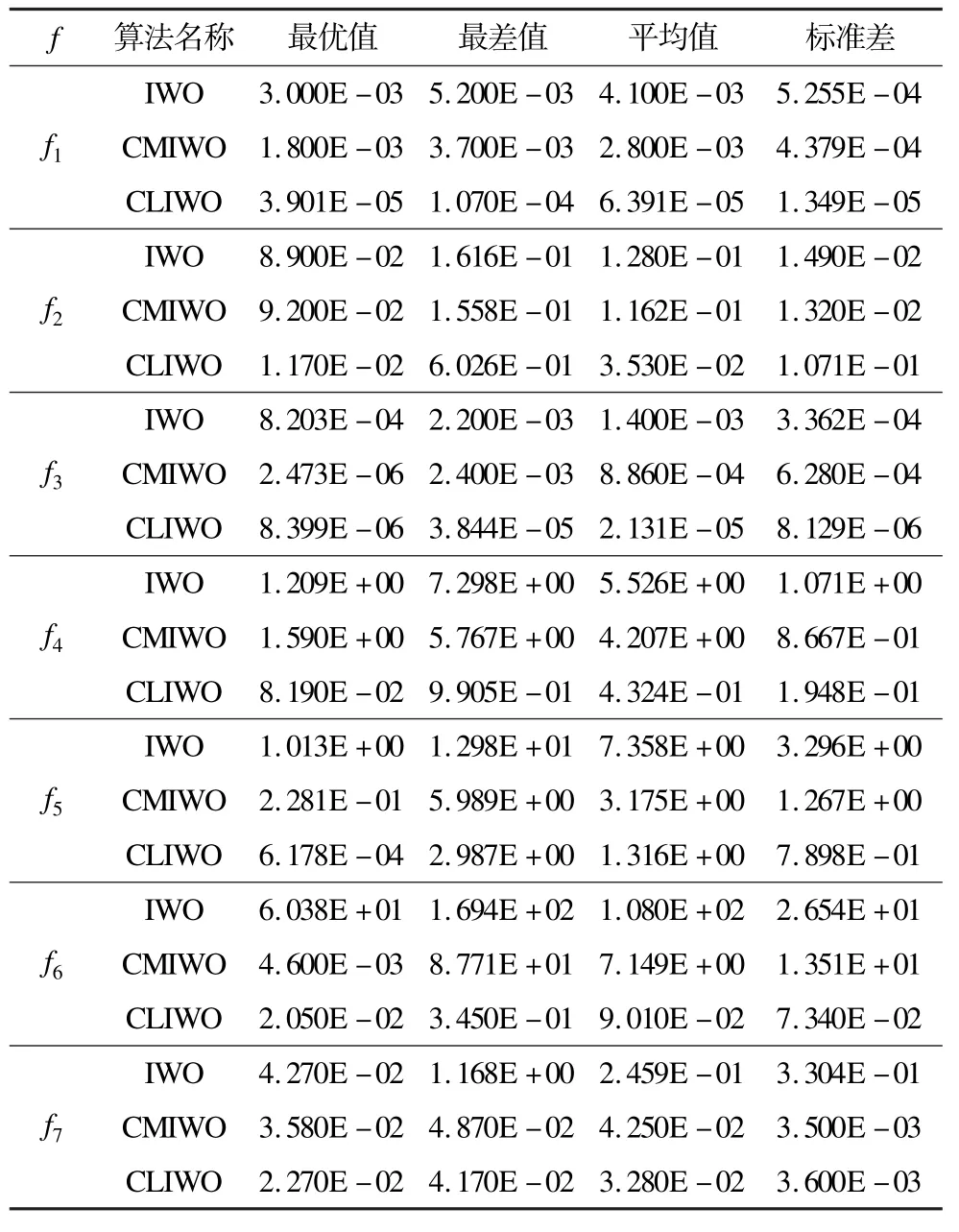
表2 7 個測試函數的實驗結果

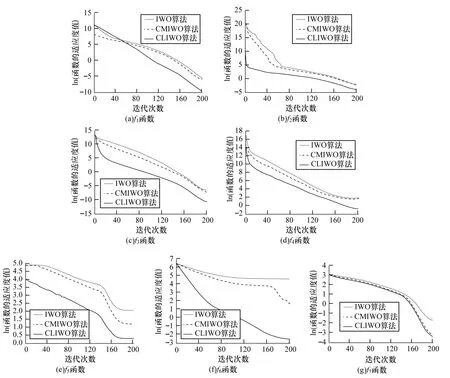
圖1 函數f1～f7適應度進化曲線

5.4 實驗結果分析

表2 從最優值、最差值、平均值和標準差4 個方面對3 種算法進行了比較。對于函數f1,f6,CLIWO得到的優化結果較其他2 種算法優勢較為明顯,平均值方面好于被比較的2 種算法2～4 個數量級。對于函數f2,f3,f4,CLIWO 得到的平均值與標準差分別優于對比的2 種算法1～2 個數量級。對于函數f5,f7,CLIWO 與CMIWO 的平均值處于同一數量級上,這是由于雖然CLIWO 根據不同種群采取不同的CR,但是每個階段的調整因子仍然是具有隨機性的,有些函數得到的優化程程度可能與CMIWO 相似。但是從數值上看CLIWO 的結果明顯優于其他2 種算法,這說明,CLIWO 算法的優化精度較高,穩定性更好。

圖1 分別描繪了函數f1～f7經200 次迭代適應度進化曲線。可以看出,對于多峰函數f7,CLIWO優化結果與CMIWO 較為接近,這也是因為CR具有隨機性取值的原因,函數f1～f6都能更為快速地收斂于更好的解。這進一步說明了CLIWO 算法收斂速度比IWO 和CMIWO 要快且優化精度較高。

6 結束語

本文將自適應分群策略引入IWO 算法,把雜草種群分為優良子群、普通子群和較差子群,對于優良子群采取較小的調整因子,對于普通的子群采取基于云模型的調整因子生成策略,對于較差子群采取較大的調整因子,因地制宜地調整算法的擴散步長。仿真實驗結果表明,本文算法在收斂速度和尋優精度上都有了明顯的提高。

[1]Mehrabian A R,Lucas C.A Novel Numerical Optimization Algorithm Inspired from Weed Colonization[J].Ecological Informatics,2006,1(4)：355-366.

[2]Zhang Xuncai,Wang Yanfeng,Cui Guangzhao,et al.Application of a Novel IWO to the Design of Encoding Sequences for DNA Computing [J].Computers and Mathematics with Applications,2009,57 (11/12)：2001-2008.

[3]Nayak M R,Krishnanand K R,Rout P K.Optimal Reactive Power Dispatch Based on Adaptive Invasive Weed Optimization Algorithm [C]//Proceedings of International Conference on Energy,Automation,and Signal.[S.l.]：IEEE Press,2011：1-7.

[4]Mallahzadeh A R,Oraizi H,Davoodi R Z.Application of the Invasive Weed Optimization Technique for Antenna Configurations [ C]//Proceedings of Conference on Antennas and Propagation.Piscataway,USA：IEEE Press,2008：425-428.

[5]蘇守寶,方 杰,汪繼文,等.基于入侵性雜草克隆的圖像聚類方法[J].華南理工大學學報：自然科學版,2008,36(5)：95-105.

[6]Zhang Xuncai,Xu Jin,Gui Guangzhao,et al.Research on Invasive Weed Optimization Based on the Cultural Framework[C]//Proceedings of the 3rd International Conference on Bio-inspired Computing：Theories and Applications.Piscataway,USA：IEEE Press,2008：129-134.

[7]Hajimirsadeghi H,Lucas C.A Hybrid IWO/PSO Algorithm for Fast and Global Optimization [C]//Proceedings of IEEE EUROCON’09.Piscataway,USA：IEEE Press,2009：1964-1971.

[8]Zhang Xuncai,Niu Ying,Gui Guanzhao,et al.A Modified Invasive Weed Optimization with Crossover Operation [C]//Proceedings of the 8th World Congress on Intelligent Control and Automation.Piscataway,USA：IEEE Press,2010：11-14.

[9]李德毅,孟海軍,史雪梅.隸屬云和隸屬云發生器[J].計算機研究與發展,1995,32(6)：15-20.

[10]李德毅,劉常昱.論正態云模型的普適性[J].中國工程科學,2004,6(8)：28-34.

[11]Zhu Yunfang,Dai Chaohua,Chen Weirong,et al.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithm Based on Cloud Generators [J].Journal of Computational Information Systems,2005,1(4)：671-678.

[12]韋杏瓊,周永權,黃華娟,等.云自適應粒子群算法[J].計算機工程與應用,2010,36(10)：233-235.

[13]陳 歡,周永權,趙光偉.基于混沌序列的多種群入侵雜草算法[J].計算機應用,2012,32(7)：1958-1961.