多變異策略差分進化算法的研究與應用

呂銘晟,沈洪遠,李志高,王 汐,龔 明,王俊年

(湖南科技大學信息與電氣工程學院,湖南 湘潭 411201)

1 概述

差分進化(Differential Evolution,DE)算法[1]采用模擬生物進化的機制,通過種群內個體差異度生成差異個體,然后進行交叉、選擇操作實現種群的進化。DE 算法適用性強,不依賴于問題輔助信息,容易實現,需要調整的參數少,非常適合于求解一些利用常規數學規劃方法不能或難以求解的復雜優化問題。

許多文獻對標準差分進化的不足提出了改進,如文獻[2-3]分別將交叉概率和縮放因子設計為自適應,文獻[4]提出采用動態更新種群的策略,文獻[5]提出一種自適應差分進化算法(SDE)；文獻[6]提出基于模糊控制的自適應差分進化算法(FADE)；文獻[7]提出基于適應值的自適應差分進化算法；文獻[8]提出自適應群體差分進化算法；文獻[9]提出廣義的變異策略方案,用戶可以方便選擇適合自己所求問題的變異操作類型；文獻[10]提出基于鄰域搜索的DE/target-to-best/1 算子；文獻[11]提出多策略和控制參數自適應差分進化算法；文獻[12]提出DE/rand/1/Either-or 算子。文獻[13]提出雙種群偽并行差分進化算法。迄今為止DE 已發展為一種在求解非線性、不可微、多峰值及高維復雜函數等類型問題的高性能強魯棒的方法,已經在濾波器設計、聚類分析等領域取得了較好的應用[14-15]。

根據變異機制的不同,DE 有多種不同版本,其中,DE/rand/1 是標準差分進化所采用的變異策略,相對而言該變異策略操作簡單,在低維單峰函數優化問題中具有收斂速度快、尋優精度高等優點。但在高維多峰復雜函數優化時,存在算法易早熟或后期收斂速度慢等不足。針對該問題,本文提出一種多變異策略差分進化算法(MDE)。通過引入改進的DE/best/1 變異策略對種群進行二次變異操作,以拓展算法搜索空間,使算法在交叉操作時能夠有更大概率獲取更多優秀的變異向量分量,進而從種群個體的“基因”上有效控制種群在進化過程中的多樣性。為避免算法進化的盲目性,在其變異操作中都采用精英保留原則,并對其中部分優秀基因采用基因擴散處理。

2 標準差分進化算法的變異策略

與其他進化類算法類似,DE 算法首先初始化種群,然后對種群個體依次執行變異、交叉和選擇操作,產生出子代種群,經過反復迭代最終得到所需的結果。

標準差分的變異策略如下：

(1) 第1 種變異策略DE/rand/1：

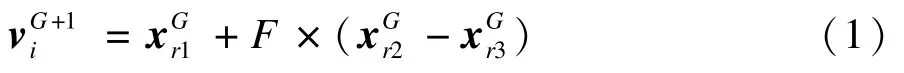
(2) 第2 種變異策略DE/best/1：

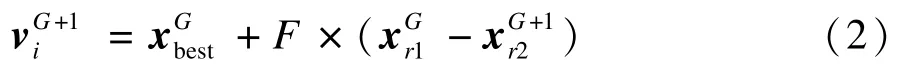
其中,r1,r2,r3∈[1,N]為隨機選擇的整數,且須滿足：r1≠r2≠r3≠i；F為變異操作縮放因子,取值在(0,2)之間,控制變異向量的幅值。

3 多變異策略差分進化算法

3.1 變異策略

差分進化算法的核心操作為變異。對變異策略的選取決定了算法在進化過程中種群的走向,而貪婪的選擇策略本身具有兩面性,在低維單峰函數優化時能夠保證算法始終向更小的方向進化,但在高維多峰復雜函數優化時,因為僅用貪婪選擇策略,致使算法一旦搜索到某一較優秀局部最小時,算法在最優適應度上出現停滯,隨著時間的累積,最終導致種群個體某些維變量陷入特定范圍。根據式(1)和式(2)可知,如果所有個體某維變量過早趨于一致,在沒有其他操作的干預下,種群喪失多樣性,算法就會出現早熟。

為了增強貪婪算法的全局最優能力,使算法在處理多峰高維復雜函數問題優化時,避免算法在某一局部最小值時可能出現的停滯,避免個體種群多樣性過早地喪失。本文采用2 種變異共存的方式優化經典差分算法。

改進變異策略DE/best/1：

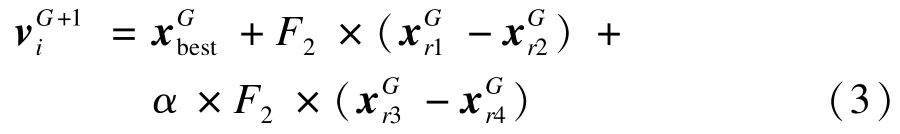
本文優化算法將2 種策略縱向結合,增加了種群的多樣性,使算法的全局搜索能力得到有效增強。將DE/rand/1 作為變異策略1。將式(3)作為變異策略2,α為向量相關參數,α的加入使本次變異有了更多的選擇空間；結合成多變異策略差分進化算法。變異策略2 的加入極大增強算法的搜索空間和在局部區域的搜索能力。MDE 算法較標準差分進化增加了多個控制參數和種群,使算法的搜索能力得到有效的加強且提供了更靈活的選擇。

差分算法使用精英保留的原則。在此基礎之上,本文研究采取了精英擴散和限制原則,使優秀的精英個體能影響其他個體的部分基因,而一些帶有欺騙性的精英個體對其影響力進行限制。這也符合生物社會的規律,即優秀的個體對整個種群的進步應產生更大的影響力。反之,應減少。

在算法中加入擴散數值k,以決定精英的影響大小。本文算法中采取每一代進化,最優個體影響其他某一個體k維基因的方法。

采取精英擴散原則后,算法能在各階段更有效地保留優勢個體,更好地發揮了多變異策略的優勢,提高了收斂速度。

3.2 算法流程

多變異策略差分進化算法的具體流程(圖1)如下：

(1) 初始化種群,對參數進行設定。

(2) 計算種群個體適應度。

(3) 采用策略1 進行變異、交叉和選擇操作。計算適應度,記錄當前最優個體。更新整個種群的適應度。

(4) 采用策略2 進行變異、交叉和選擇操作。計算適應度,記錄當前最優個體。更新整個種群的適應度。將策略2 中最優個體的部分基因根據擴散數值k替代隨機個體的對應基因。

(5) 判斷步驟(4)得到的結果是否達到退出條件,若滿足,結束,否則,跳轉到步驟(2)繼續執行。

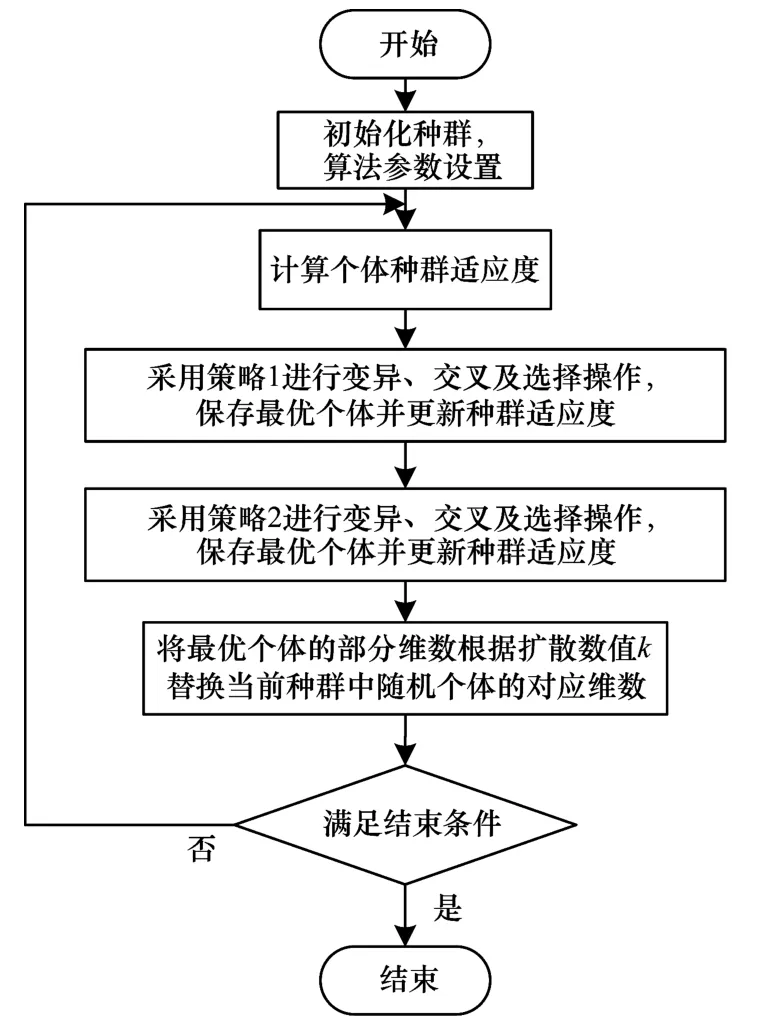
圖1 多變異策略差分進化算法流程

4 算法測試與結果分析

4.1 測試環境與結果

為驗證MDE 的有效性,以常用的4 個Benchmark測試函數為例對MDE 進行測試,同時,與標準差分DE/rand/1 進行對比。算法最大函數評價次數為2.5e +05,各算法對于每個函數都獨立連續運行20 次。

表1 中,CR1,CR2分別表示DE/rand/1、DE/best/1 2 種變異策略下算法的交叉概率；F1,F2分別表示縮放因子；α為相關系數；k為擴散系數。

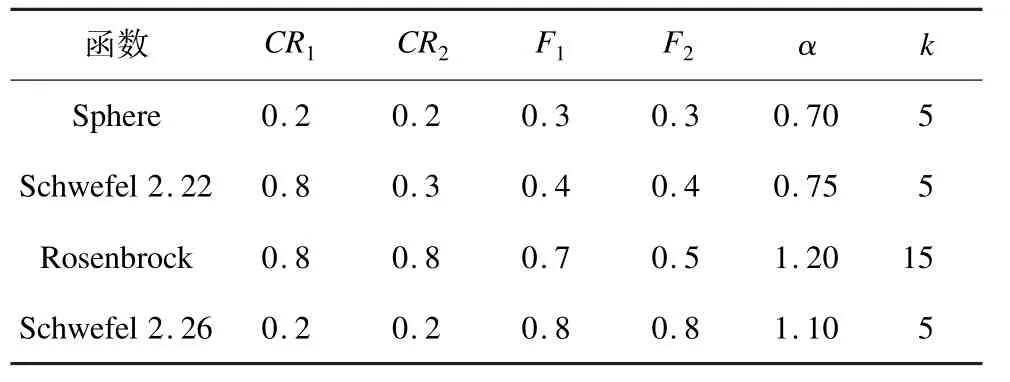
表1 MDE 算法各控制參數設置

由表2 結果可知,當DE/rand/1 出現早熟現象時,DE/best/1 能夠通過參數的調節防止算法早熟,可見其穩定性不如DE/rand/2。正是由于F2的存在彌補了DE/rand/1 穩定性的不足。而DE/rand/1 和DE/best/1 串行組合并非簡單疊加,在結合兩者優點的基礎上,MDE 性能有了進一步的提高,使其整體性能在測試中表現最為優秀。

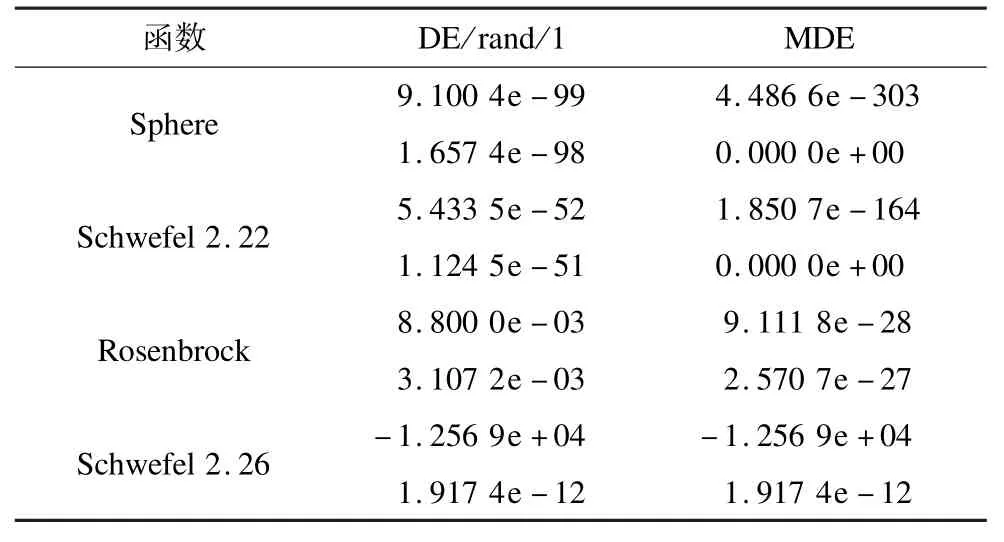
表2 20 次獨立運行的最優解平均值

從算子的結構上進行分析,式xr1+F×(xr2-xr3)可分為2 個部分理解,xr1作為隨機選擇的基向量,F1×(xr2-xr3)可理解為以基向量為中心在其周圍進行局部搜索。可見式(1)本身就兼有全局與局部搜索的特性,只是其全局搜索強于局部搜索。將式(2)改寫為(xbest+F2× (xr2-xr3)) +α×F2×(xr4-xr5)),當α≠0 時,改進后的DE/best/1 相對于DE/best/1 而言多進行了一次變異,可以理解為改進后DE/best/1 其實是局部搜索能力得到加強的DE/best/1。并且DE/best/1 以當前最優個體為指引進行局部搜索,減少了其盲目性。同時,其隨機性也擴展了算法的搜索空間,有利于增加種群的多樣性。有效地提升了算法的整體性能。

4.2 參數設置

交叉概率CR雖不能對交叉操作提供精確的指導信息,但是通過對其數值大小的調節能夠控制算法獲取變異向量分量的能力,當CR較大時,在交叉操作中能以較大的概率從變異向量獲取更多的分量,擴展算法的搜索空間；相反,則利于種群的多樣性。CR2取值應該不小于CR1,原因是DE/best/1 策略較DE/rand/1 策略能產生更多的優秀變異向量分量,而這些分量需要較大的交叉概率獲取。F2取值應少于F1,這是因為經過DE/rand/1 策略優化后問題的解已經向最優靠攏,而策略2 可以理解為是在前者的基礎上微調,根據向量合成法則,F2和α×F2不宜較F1大。這有利于平衡算法的全局和局部搜索能力。當然還應該由具體問題的特性來設置F2和α,使算法的性能發揮出較好的優勢,提高解決問題的效率。對于單峰函數的求解CR2取較大的值,有利于從DE/best/1 變異中獲取更多優秀變異分量,使結果的精度越高。對于其他復雜的多峰函數,由于存在大量局部最小值欺騙,算法只能同時以較小的CR2逐步從DE/best/1 變異中獲取優秀變異分量。

對縮放因子F的設置也必須考慮具體問題的特性,從數學表達式可以看出F2和α×F2是2 個可以互換的參數,因此,實驗中3 個取值比較接近,也可以理解α×F2是在F2基礎上的一種微調。因此,α的取值一般在1 附近。

擴散參數k的加入是為了使算法能在各階段更有效地保留真正的優勢個體及其潛在優勢基因段,是對策略2 的很好補充,有效避免陷入早熟的問題。k的選取以種群個體維數M為度量,實驗表明,k取(0.1～0.5)M,能對算法產生較好影響。

圖2～圖5 為4 個測試函數的仿真對比,本文將MDE 的實驗結果和標準DE/rand/1 的結果以及將標準DE/rand/1 策略2 倍線性疊加的結果就行了比較。其中,DE 為標準差分；2XDE 為標準DE 線性疊加；MDE 為改進后的差分算法。

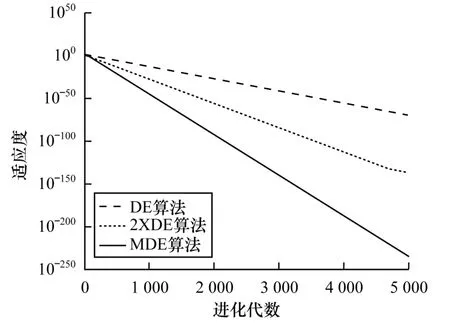
圖2 Schwefel 2.22 函數適應度比較

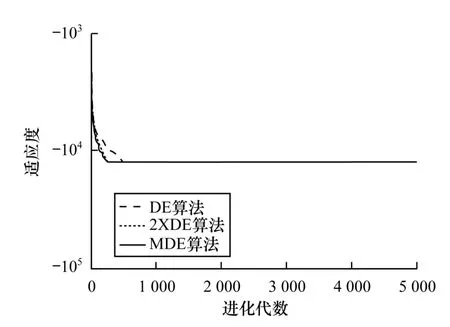
圖3 Schwefel 2.26 函數適應度比較

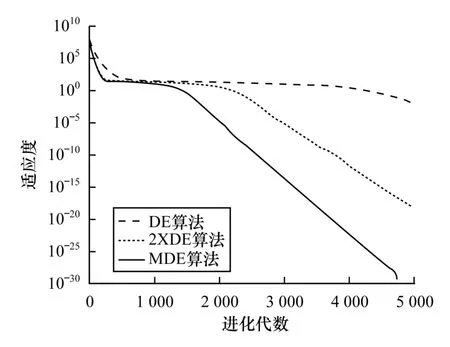
圖4 Rosenbrock 函數適應度比較

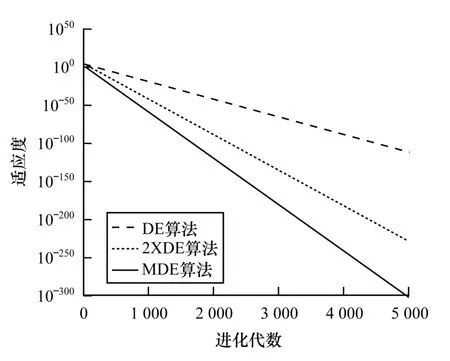
圖5 Sphere 函數適應度比較

5 電力負載分配問題

本文采用一個經典的38 個發電機的電力負載分配問題,發電機成本與發電量之間的關系如下：

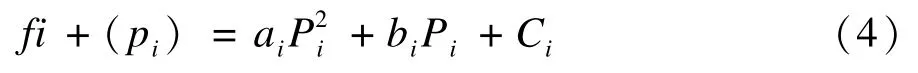
電機功率約束為：

電力平衡約束為：

當電力系統覆蓋密集時可以忽略網絡損耗,本文在計算中忽略了網絡損耗,故電力平衡約束可簡化為：

目標函數：

總負荷PD=6 000 mW。為了克服隨機性影響,算例獨立計算20 次。

表3 給出了算法的運算結果,以及與ISPO[16]算法的比較。本次測試中樣本個數為50 個,迭代次數為10 00 次,F1=0.4,F2=0.4,α=0.75,CR1=0.3,CR2=0.3,k=5。由表3 可知,此算法取得了相對較好的結果。

表3 2 種算法的目標函數計算結果比較

MDE 算法的目標函數值最優曲線如圖6 所示,由圖可知,此方法求解經典電力負載分配問題快速有效。表4 為各發電機目標函數最優解。

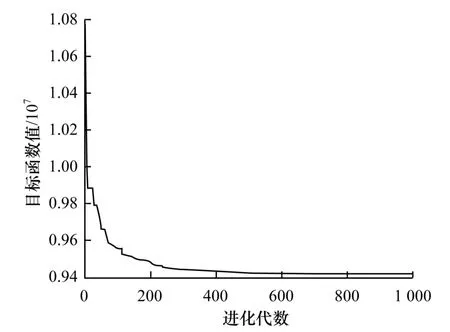
圖6 MDE 算法的目標函數最優曲線

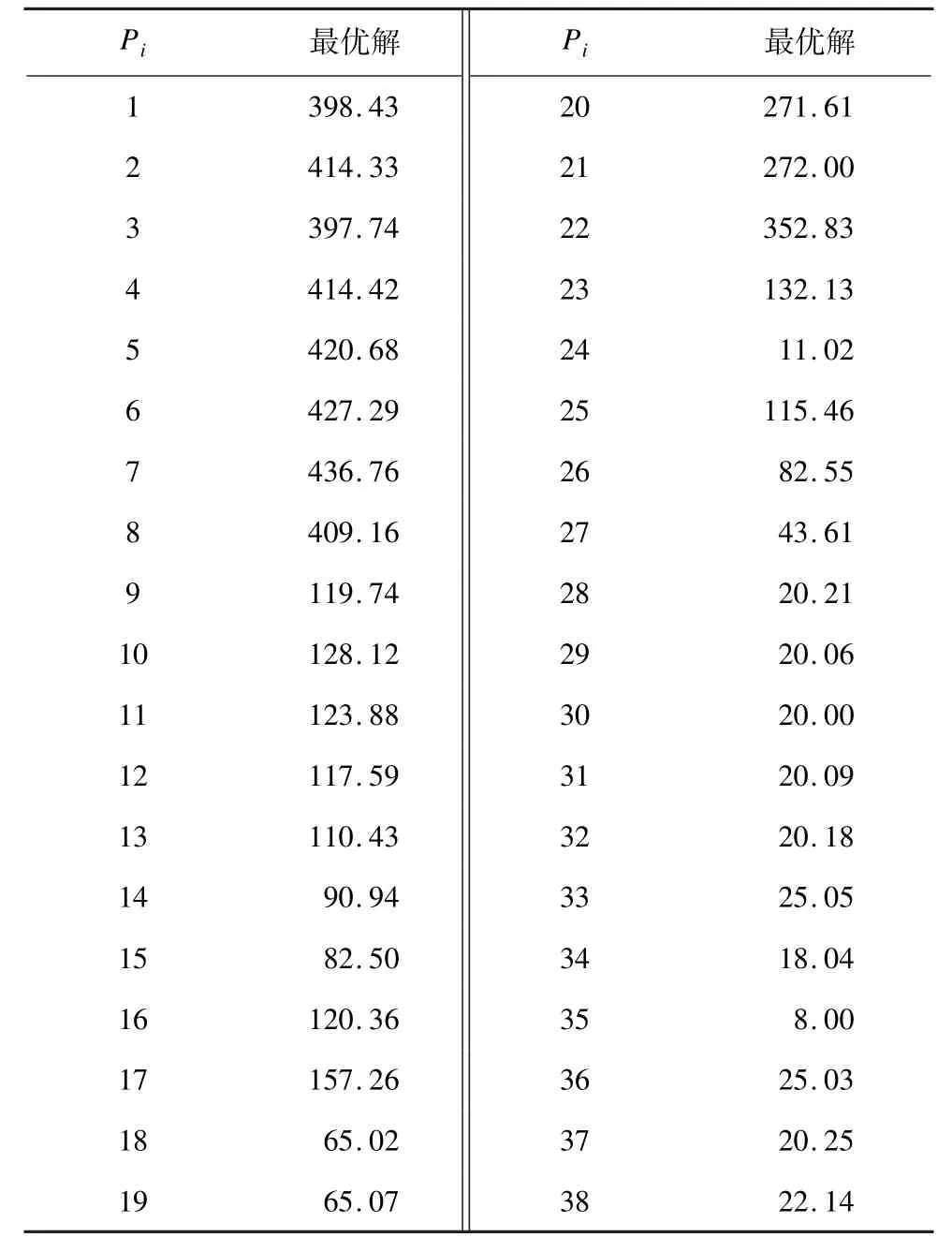
表4 各發電機MDE 算法的目標函數最優解

6 結束語

本文針對標準差分進化在高維多峰復雜函數優化中存在的不足,設計一種多變異策略差分進化算法。在4 個Benchmark 函數上與標準差分進化算法進行了對比,結果表明,改進算法在對算法的控制方面較標準差分進化算法更為靈活而且穩定,收斂速度和所得最優解精度方面都比標準差分進化算法有明顯優勢。通過電力負載分配模型求解結果表明,該算法是求解大規模電力系統經濟負荷分配問題的有效方法。今后將在多變異的基礎上,研究參數的自適應設置。

[1]Storn R,Price K.Differential Evolution——A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,11(4)：341-359.

[2]許小健,黃小平,錢德玲.自適應加速差分進化算法[J].復雜系統與復雜性科學,2008,5(1)：87-92.

[3]鄧澤喜,劉曉冀.差分進化算法的交叉概率因子遞增策略研究[J].計算機工程與應用,2008,44(27)：33-36.

[4]肖術駿,朱學峰.一種改進的快速高效的差分進化算法[J].合肥工業大學學報：自然科學版,2009,32(11)：1700-1703.

[5]Salman A,Engelbrecht A P,Omran M G H.Empirical Analysis of Self-adaptive Differential Evolution[J].European Journal of Operational Research,2007,183(2)：785-804.

[6]Liu J,Lampinen J.A Fuzzy Adaptive Differential Evolution Algorithm[J].Soft Computing,2005,9 (6)：448-462.

[7]Ali M M,T?rn A.Population Set-based Global Optimization Algorithms：Some Modifications and Numerical Studies[J].Computers &Operations Research,2004,31(10)：1703-1725.

[8]Teng N S,Teo J,Hijazi M H A.Self-adaptive Population Sizing for a Tune-free Differential Evolution[J].Soft Computing,2009,13(7)：709-724.

[9]Feoktistov V,Janaqi S.Generalization of the Strategies in Differential Evolution[C]//Proceedings of the 18th International Parallel and Distributed Processing Symposium.[S.l.]：IEEE Press,2004：165-170.

[10]Das S,Abraham A,Chakraborty U K,et al.Differential Evolution Using a Neighborhood-based Mutation Operator[J].IEEE Transactions on Evolutionary Computation,2009,13(3)：526-553.

[11]Pan Quanke,Suganthan P N,Wang Ling,et al.A Differential Evolution Algorithm with Self-adapting Strategy and Control Parameters[J].Computers &Operations Research,2011,38(1)：394-408.

[12]Price K,Storn R M,Lampinen J A.Differential Evolution：A Practical Approach to Global Optimization[M].[S.l.]：Springer,2006.

[13]吳亮紅,王耀南,周少武,等.雙種群偽并行差分進化算法的研究與應用[J].控制理論與應用,2007,24(3)：453-459.

[14]Paterlini S,Krink T.Differential Evolution and Particle Swarm Optimisation in Partitional Clustering[J].Computational Statistics &Data Analysis,2006,50(5)：1220-1247.

[15]Storn R.Designing Nonstandard Filters with Differential Evolution[J].Signal Processing Magazine,2005,22(1)：103-106.

[16]Chaturvedi K T,Pandit M,Srivastava L.Particle Swarm Optimization with Time Varying Acceleration Coefficients for Non-convex Economic Power Dispatch[J].International Journal of Electrical Power &Energy Systems,2009,31(6)：249-257.