兩棲自行火炮水上橫向射擊穩(wěn)定性仿真分析

蔣華劍，郭保全，孫明顏

(中北大學 機電工程學院，山西 太原030051)

0 引 言

兩棲登陸作戰(zhàn)是現(xiàn)代戰(zhàn)爭的一種重要作戰(zhàn)形式。在登陸作戰(zhàn)中，具備兩棲作戰(zhàn)能力的自行火炮已成為機動作戰(zhàn)部隊搶灘登陸的重要武器裝備。兩棲自行火炮進行水上射擊時，車體在水中會產(chǎn)生6 個方向的搖蕩運動。尤其是在水上橫向射擊時，產(chǎn)生的大幅度橫搖運動對其穩(wěn)定性威脅最大。從現(xiàn)有文獻來看，馬新謀、潘玉田等［1－2］對兩棲武器在非射擊狀態(tài)下的線性與非線性橫搖動力學做了較多研究，郭昭蔚、何安民等［3］對兩棲武器水上縱向射擊動力學做了一定研究，但是對橫向射擊穩(wěn)定性的研究尚未得見。針對這一問題，本文利用Pro/Engineer和ABAQUS 建立了某兩棲火炮的剛?cè)狁詈隙囿w發(fā)射動力學模型，并利用ADAMS 軟件對其進行了橫向射擊動力學仿真分析，進而尋找出兩棲自行火炮水上橫向射擊時的高低安全射角。

1 橫向射擊條件與基本假設

研究兩棲自行火炮水上橫向射擊的發(fā)射動力學特性，需要給定一定的合理假設，以簡化問題，提高計算效率。為此，本文給出以下射擊條件與基本假設:

1)兩棲自行火炮在無限廣靜水域中進行橫向射擊，不考慮波浪載荷和風速的影響;

2)兩棲自行火炮的形狀與質(zhì)量左右對稱;

3)只將身管作為柔性體考慮，其他部分認定為剛體;

4)不考慮炮彈彈帶的擠進過程;

5)考慮彈丸與膛線身管的剛?cè)狁詈辖佑|/碰撞，考慮身管與搖架的剛?cè)峤佑|/碰撞/滑移，考慮高低機主齒輪與搖架齒弧的接觸/碰撞，考慮搖架耳軸與耳軸室的接觸/碰撞。

2 剛?cè)狁詈习l(fā)射動力學仿真模型的建立

2.1 三維模型與全炮拓撲關(guān)系建立

三維實體建模，是多體動力學建模的基礎。準確的三維模型能夠保證對剛體接觸判斷與計算的準確性，同時也對柔體的模態(tài)計算、柔體間接觸/碰撞的處理產(chǎn)生重要影響［4］。本文按某兩棲輪式自行火炮機構(gòu)運動特點，在Pro/Engineer 中進行三維建模，然后將模型后導入ADAMS/View 中(身管使用ABAQUS 劃分網(wǎng)格后，通過MNF 中性文件導入)，其水上橫向射擊仿真模型如圖1所示。

圖1 某兩棲自行火炮水上橫向射擊動力學仿真模型Fig.1 Dynamics simulation model of an amphibious self-propelled gun when lateral firing on water

某兩棲自行火炮簡化模型全炮拓撲關(guān)系如圖2所示。鉸Hi(i=1，3，5，10，12，13，14)為接觸副，鉸Hj(j=4，6，7，9，11，15)為固定副，鉸Hk(k=8)為滑移副，鉸Hw(w=2)為旋轉(zhuǎn)副。

為了方便模型的求解和仿真結(jié)果的分析，如圖3所示，建立5 個參考坐標系:OXY 為慣性坐標系，O 點位于ADAMS/View 仿真平臺的原點(0，0，0);O1X1Y1為車體坐標系，原點O1位于車體重心位置;O2X2Y2為后座部分坐標系，原點O2位于后座部分重心位置，X2軸與身管軸線平行;O3X3Y3為搖架坐標系，原點O3位于搖架左右兩耳軸中心連線的中點;O4X4Y4為炮塔坐標系，原點O4位于炮塔重心位置。后4 個坐標系均與慣性坐標系平行。

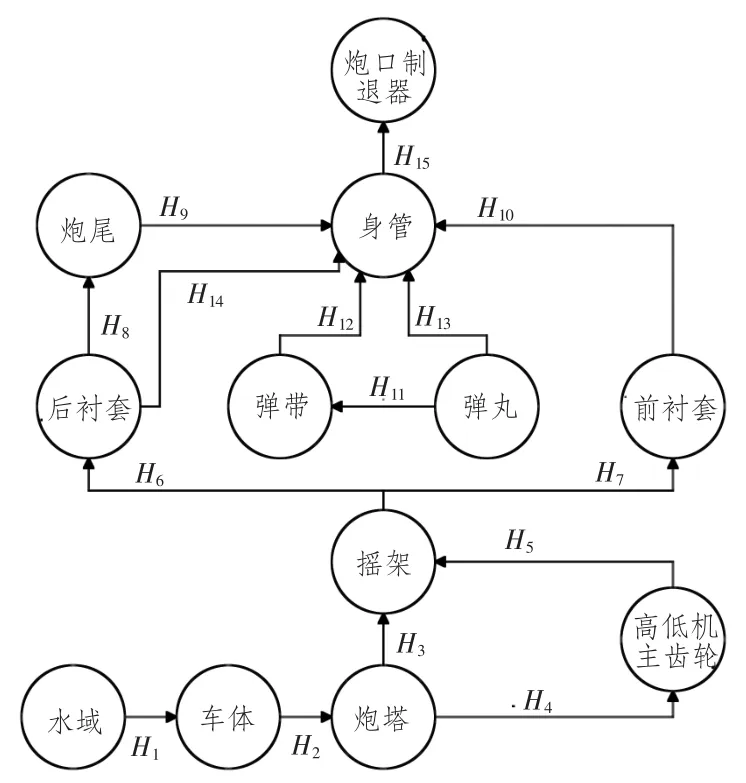
圖2 某兩棲自行火炮拓撲結(jié)構(gòu)圖Fig.2 Topological structure of an amphibious self-propelled gun

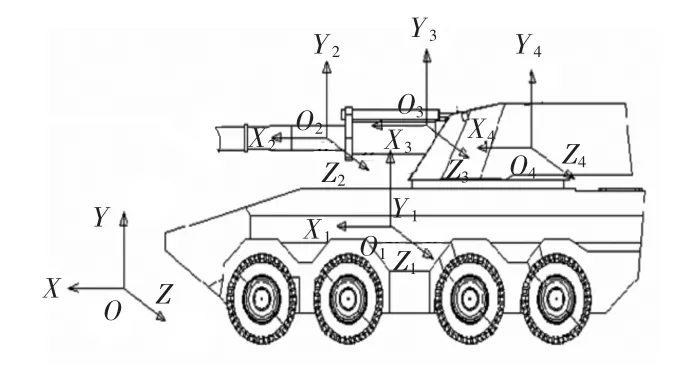
圖3 某兩棲自行火炮坐標系圖Fig.3 Coordinates system diagram of an amphibious self-propelled gun

2.2 某兩棲自行火炮水上射擊載荷建模

某兩棲自行火炮水上射擊時的載荷分析如圖4所示。

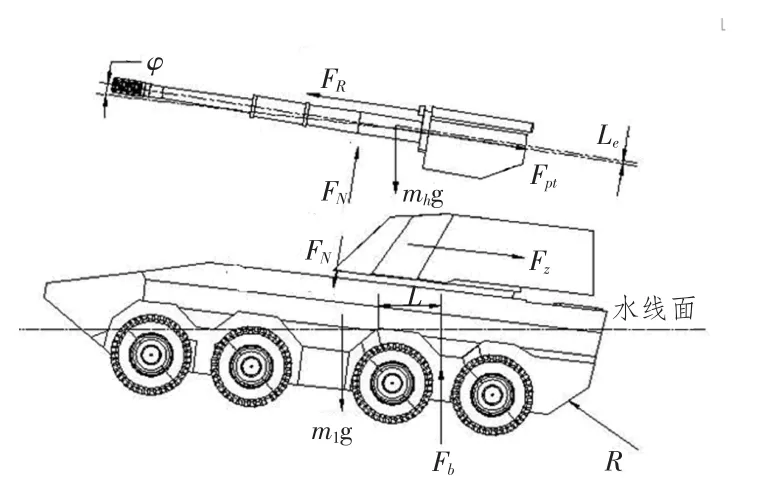
圖4 某兩棲火炮水上射擊時的載荷分析Fig.4 Loads analysis of an amphibious self-propelled gun when firing on water

圖中，φ 為火炮的高低射角;FR為后坐阻力，包括制退機液壓阻力、復進機力、密封裝置的摩擦阻力等;Fpt為炮膛合力，作用在炮膛軸線上;FN為搖架導軌提供的法向反力;mhg 為后坐部分的重力;Le為后坐部分質(zhì)心到身管軸線的距離;m1g 為非后坐部分的重力;Fb為浮力;R 為水阻力;L 為浮力到全炮質(zhì)心的距離。

1)炮膛合力的建模

火藥氣體對炮身的作用合力Fpt主要來自于膛底、坡膛以及氣體流動對膛壁的摩擦力。氣體與身管內(nèi)膛壁的摩擦力與前兩者相比，可以忽略。則Fpt的計算公式如下［5］:

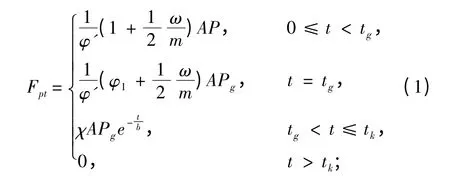
其中，

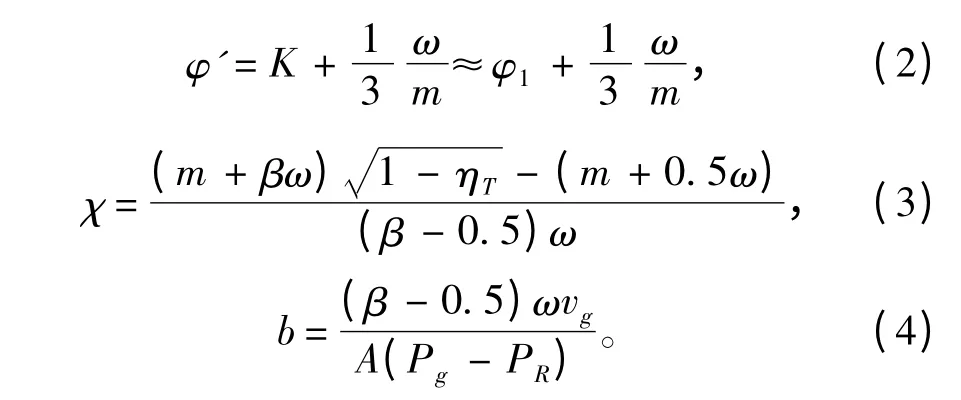
式中:φ′ 為次要功計算系數(shù);φ1為僅考慮彈丸旋轉(zhuǎn)和摩擦2 種次要功計算系數(shù);m 為彈丸質(zhì)量;ω 為裝藥質(zhì)量;A 為炮膛橫斷面面積;P 為火藥氣體平均壓力;Pg為彈丸出炮口瞬間的炮口壓力;χ 為炮口制退器沖量特征值;b 為火藥氣體時間常數(shù);tg，tk分別為彈丸出炮口和后效期結(jié)束時的時刻;ηT為炮口制退器的效率;β 為無炮口制退器時的火藥氣體作用系數(shù);vg為彈丸出炮口瞬間的速度;PR為后效期結(jié)束時膛內(nèi)火藥氣體平均壓力。

2)后坐阻力的建模

后坐阻力方程為:

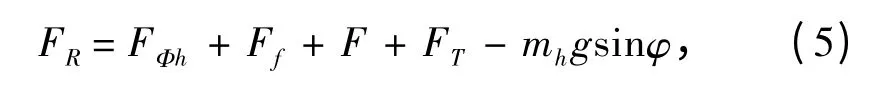
其中，

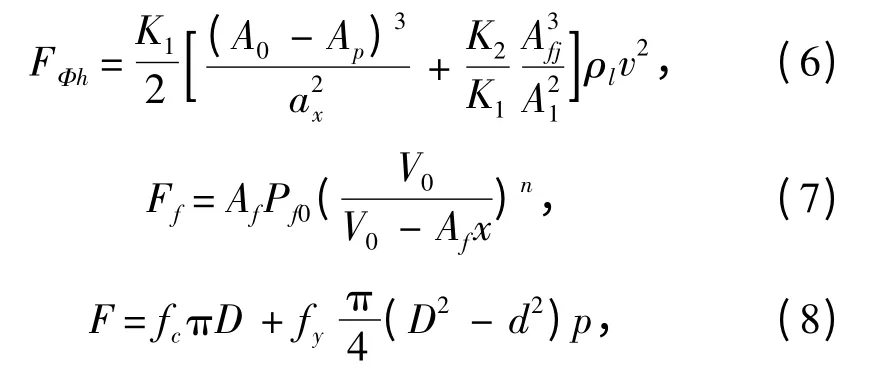
式中:FΦh為駐退機力;Ff為復進機力;F 為密封裝置摩擦力;FT為搖架導軌上的摩擦力［5］;mh為后坐部分質(zhì)量;φ 為火炮射角;A0為駐退機活塞工作面積;AP為節(jié)制環(huán)孔的面積;Afj為復進節(jié)制器的工作面積;ax為節(jié)制桿任意截面對應的流液孔的面積;A1為支流最小截面的面積;K1為主流液阻力系數(shù);K2為支流液阻力系數(shù);ρl為液體的密度;v 為后坐速度;Af為復進機活塞工作面積;x 為后坐位移;Pf和Pf0分別為任一瞬時復進機中氣體壓力和氣體初壓;V和V0分別為任一瞬時復進機中氣體的容積和氣體的初始容積;n 一般取1.3;D 為相對運動表面的直徑;d 為放置橡膠“O”型圈的矩形槽底的直徑;p 為液體的壓力;fc和fy分別為選用橡膠“O”型圈的摩擦系數(shù)和承壓后橡膠“O”型圈附加的摩擦系數(shù);μ 為搖架導軌的等效摩擦系數(shù)，取0.16 ～0.2。

3)浮力和浮力矩的建模

利用三維軟件的二次開發(fā)，可獲取車體在任意姿態(tài)、任意位置下浸入水中部分的體積［6］，則由阿基米德原理可得浮力大小為:

式中:ρ 為水的密度;Vl為車體浸入水中體積。

調(diào)用三維軟件中的質(zhì)量特性工具，可以求出車體任意姿態(tài)、任意位置排開水的體積的幾何中心相對于車體質(zhì)心的坐標，也就是浮力的作用點，從而可以求出浮力到全炮質(zhì)心的距離L，進而求出浮力矩:

4)水阻力和水阻力矩的建模

車體在水中受到的動阻力主要由摩擦阻力Rf和剩余阻力Rr兩部分組成［7］，即:

兩棲自行火炮在水中所受摩擦阻力，相當平板的摩擦阻力與粗糙度增加的摩擦阻力之和。

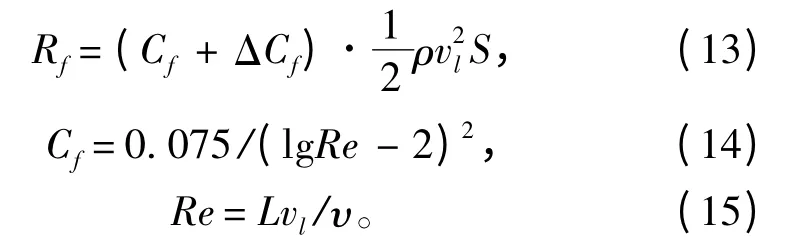
式中:Rf為摩擦阻力;ΔCf為附加阻力系數(shù);Cf為摩擦阻力系數(shù);vl為車體在水中的速度;S 為車體浸入水中部分的表面積;Re 為雷諾數(shù);L 為車輛水線長;υ 為運動粘性系數(shù)，當水溫為12°時，取1.239×10-6m2·s-1。

剩余阻力為:

式中:ξ 為與車體外形系數(shù);S1為車體浸入水中部分的最大橫剖面積。

ξ和n 由某兩棲自行火炮拖模實驗結(jié)果擬合得出，最大橫切剖面S1為車體浸入水中部分在其速度矢量vl方向的最大投影。

調(diào)用三維軟件中的截面屬性模塊，計算出最大橫切剖面相對于車體質(zhì)心的坐標，進而求出阻力矩:

式中l(wèi)R為投影截面形心到車體質(zhì)心的距離。

3 剛?cè)狁詈夏Ｐ偷乃蠙M向射擊動力學仿真計算

3.1 動力學數(shù)值仿真結(jié)果

在ADAMS 中，對前文所建立的兩棲自行火炮模型進行橫向射擊仿真，車體在慣性坐標系OXY 下的運動結(jié)果如圖5 ～圖10所示。

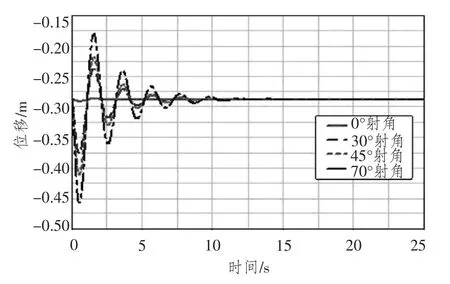
圖5 升沉位移Fig.5 Heave displacement

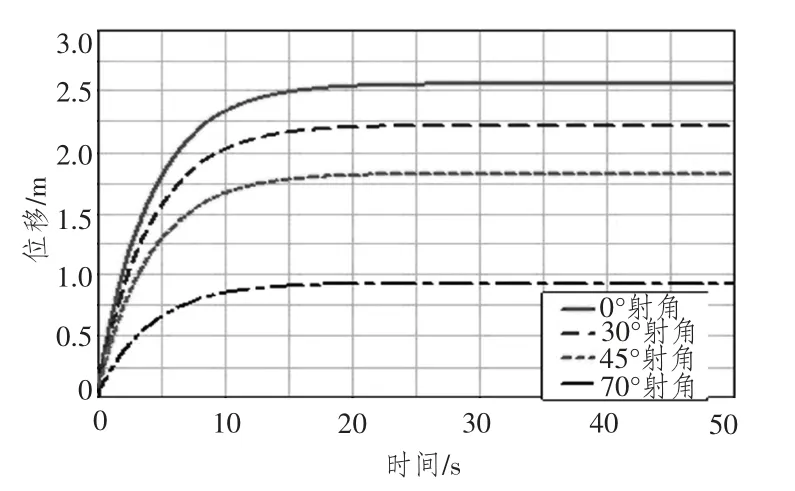
圖6 橫移位移Fig.6 Lateral displacement

圖7 縱移位移Fig.7 Longitudinal displacement

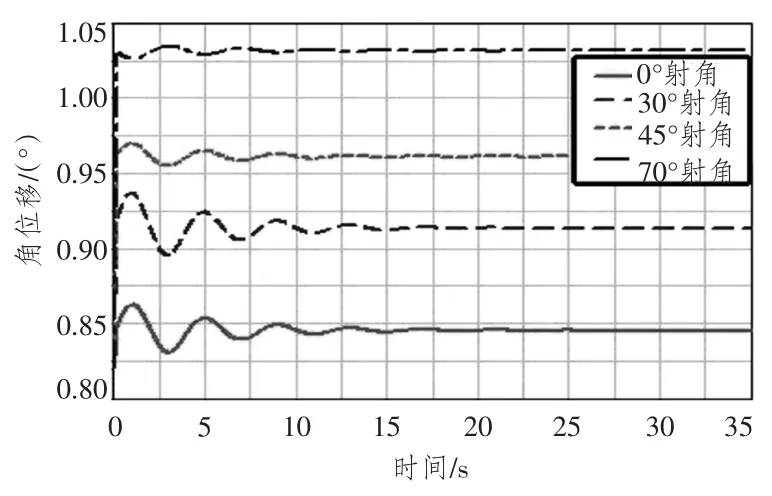
圖8 縱搖角Fig.8 Angle of pitching

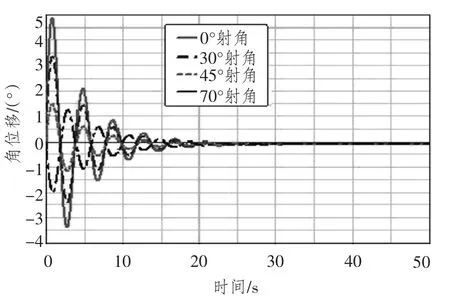
圖9 橫搖角Fig.9 Angle of roll

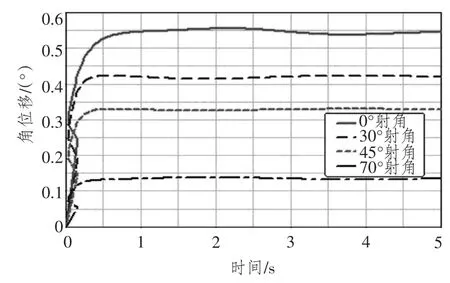
圖10 首搖角Fig.10 Angle of yaw

3.2 數(shù)據(jù)分析

1)車體的升沉位移隨著射角的增大而增大;車體的橫移位移隨著射角的增大而減小，且數(shù)值總體較大，0°射角時甚至超過2.5 m;車體的縱移位移隨著射角的增大而增大，但數(shù)值總體較小，最大不超過0.125 m。可見，后坐力在橫向和豎直方向上的分力是車體在水中橫移和升沉運動的主要因素。

2)車體的縱搖角隨著射角的增加而增加。這是因為后坐阻力矩在縱搖方向上的分量與浮力矩之和是產(chǎn)生車體縱搖的主要因素，且2 個力矩方向相同。隨著射角的增加，后坐阻力矩減少的程度要小于浮力矩增加的程度，即兩力矩之和隨著射角的增大而增大，故而引起縱搖角隨之增大。

3)車體的橫搖角和首搖角隨著射角的增大而減小。當射角為70°時，橫搖角為負值，說明車體左傾。這是因為隨著射角的增大，使車體橫搖的后坐力矩逐漸減小，當射角增大到一定角度后，作用在搖架上的后坐阻力逐漸偏向車體重心的左側(cè)。

4)在0°射角時，車體的橫搖角達到極限值，接近5°，對于某兩棲自行火炮來說，比較危險;在射角為70°時，車體的升沉位移達到極限值0.46m，尚未超過車體的干舷。

可見，兩棲自行火炮在靜水中進行橫向射擊時，高低射角越小，其偏離航線和發(fā)生橫向傾覆的可能性就越大;而在較大射角時，雖然升沉位移和縱搖角均有所增大，但是均在安全范圍以內(nèi)。所以，該兩棲自行火炮在進行水上橫向射擊時，應盡量避免小射角射擊。

4 結(jié) 語

本文以某兩棲自行火炮水上橫向射擊穩(wěn)定性為研究對象，首先在ADMAS/View 中建立了某兩棲自行火炮的多體動力學模型，考慮了剛體間的接觸/碰撞、柔體間的接觸/碰撞和剛?cè)狁詈辖佑|/碰撞等復雜因素。并借鑒船舶理論，對兩棲自行火炮車體在水中的水阻力和水阻力矩進行了建模。最后，通過對剛?cè)狁詈夏Ｐ偷乃蠙M向射擊仿真結(jié)果進行分析，得出了兩棲自行火炮在靜水中橫向射擊時應盡量避免小射角，以提高橫向射擊穩(wěn)定性的結(jié)論。

［1］馬新謀，潘玉田，馬昀．兩棲作戰(zhàn)武器線性橫搖運動動力學分析［J］．火炮發(fā)射與控制學報，2008(2):85－88．

MA Xin-mou，PAN Yu-tian，MA Yun．Linear roll motion dynamics analysis of amphibious combat weapon［J］．Journal of Gun Launch ＆ Control，2008(2):85－88．

［2］馬新謀，潘玉田，常列珍，等．兩棲作戰(zhàn)武器非線性橫搖動力學研究［J］．火炮發(fā)射與控制學報，2010(4):66－69．

MA Xin-mou，PAN Yu-tian，CHANG Lie-zhen，et al．Study on nonlinear rolling motion dynamics of amphibious combat weapon［J］．Journal of Gun Launch ＆ Control，2010(4):66－69．

［3］郭昭蔚，何安民，劉海民，等．兩棲裝甲車輛水上射擊位移規(guī)律仿真研究［J］．計算機仿真，2013，30(1):54－58．

GUO Zhao-wei，HE An-min，LIU Hai-min，et al．Simulation research on displacement rule of amphibious armored vehicles shooting in water［J］．Computer Simulation，2013，30(1):54－58．

［4］曾晉春．車載式火炮剛?cè)狁詈习l(fā)射動力學研究［D］．南京:南京理工大學，2010．

ZENG Jin-chun．Study on the rigid-flexible couple launch dynamics of truck-mounted guns［D］．Nanjing:Nanjing University of Science ＆ Techndogy，2010．

［5］高躍飛．火炮反后坐裝置設計［M］．北京:國防工業(yè)出版社，2010．

GAO Yue-fei．Artillery recoil design［D］．Beijing:National Defense Industry Press，2010．

［6］李美彥，郭保全，潘丹陽．基于Solidworks 二次開發(fā)的兩棲武器浮心與浮態(tài)計算方法研究［J］．火炮發(fā)射與控制學報，2010(3):5－8．

LI Mei-yan，GUO Bao-quan，PAN Dan-yang．Computational method on buoyancy center and floating state of amphibian weapons based on solidworks secondary development［J］．Journal of Gun Launch ＆ Control，2010(3):5－8．

［7］盛振邦．船舶原理［M］．上海:上海交通大學出版社，2003．

SHENG Zhen-bang．Ship theory［M］．Shanghai:Shanghai Jiaotong University Press，2003．