基于統(tǒng)計(jì)方法對(duì)新疆環(huán)境污染的研究——以新疆工業(yè)各行業(yè)為例

崔金蕾 李國東

(新疆財(cái)經(jīng)大學(xué)應(yīng)用數(shù)學(xué)學(xué)院，新疆 烏魯木齊 830012)

在經(jīng)濟(jì)迅猛發(fā)展的同時(shí)，環(huán)境相應(yīng)著也發(fā)生了變化。環(huán)境的污染越來越嚴(yán)重，部分省市出現(xiàn)了嚴(yán)重的霧霾，水體被污染等現(xiàn)象，這危害著人類的生存。盡管政府采取了一定的措施，但是經(jīng)濟(jì)的發(fā)展對(duì)環(huán)境的破壞不是一蹴而就的，因此對(duì)環(huán)境的治理效果也不一定有顯著的成效。新疆是一個(gè)重工業(yè)基地，對(duì)產(chǎn)品進(jìn)行初加工，不可避免的要有大量的廢水廢氣的排放，這就需要對(duì)各個(gè)行業(yè)各個(gè)部門有一個(gè)詳盡的分析，得出工業(yè)中對(duì)環(huán)境的污染最大的行業(yè)，對(duì)治理有一定的針對(duì)性，進(jìn)行綜合治理。

從國內(nèi)外的文獻(xiàn)來看，很多專家學(xué)者研究經(jīng)濟(jì)的發(fā)展對(duì)于環(huán)境污染的影響，如1991～2011年甘肅省經(jīng)濟(jì)增長(zhǎng)環(huán)境污染研究[1]；各個(gè)區(qū)域?qū)Νh(huán)境污染的研究，如我國區(qū)域城市化與環(huán)境污染關(guān)系的空間計(jì)量研究[2]，河南省產(chǎn)業(yè)結(jié)構(gòu)升級(jí)與環(huán)境污染關(guān)系研究[3]等等。本文以新疆工業(yè)中各行業(yè)為例，現(xiàn)在將用統(tǒng)計(jì)的一些方法對(duì)工業(yè)中廢水廢氣的排放進(jìn)行分析，得出應(yīng)加強(qiáng)管理行業(yè)類別的結(jié)論。

現(xiàn)借鑒《2013年新疆統(tǒng)計(jì)年鑒》中的數(shù)據(jù)，將其整理如下：

行業(yè)分為農(nóng)副食品加工業(yè)、食品制造業(yè)、酒、飲料和精制茶制造業(yè)、紡織業(yè)、造紙及紙制品業(yè)、石油加工、煉焦及核燃料加工業(yè)、化學(xué)原料及化學(xué)制品制造業(yè)、化學(xué)纖維制造業(yè)、黑色金屬冶煉及壓延加工業(yè)、電力、熱力的生產(chǎn)和供應(yīng)業(yè)、其他行業(yè)，分別簡(jiǎn)稱為農(nóng)品加工、食品制造、副食制造、紡織業(yè)、紙制品業(yè)、燃料加工、原料制造、纖維制造、金屬加工、電熱產(chǎn)供、其他行業(yè)，如表1所示[4]：

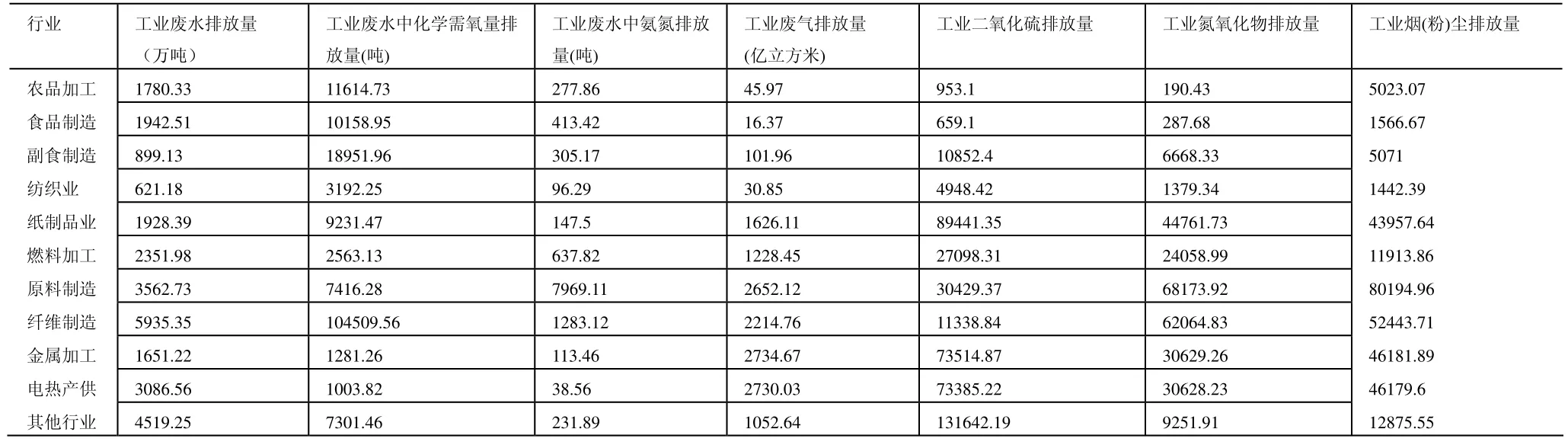
表1 工業(yè)按行業(yè)重點(diǎn)調(diào)查工業(yè)企業(yè)廢水廢氣及污染物排放情況

1 基本原理

1.1 主成分分析基本思想

主成分分析是設(shè)法將原來眾多具有一定相關(guān)性（比如P個(gè)指標(biāo)），重新組合成一組新的互相無關(guān)的綜合指標(biāo)來代替原來的指標(biāo)。主成分分析，是考察多個(gè)變量間相關(guān)性一種多元統(tǒng)計(jì)方法，研究如何通過少數(shù)幾個(gè)主成分來揭示多個(gè)變量間的內(nèi)部結(jié)構(gòu)，即從原始變量中導(dǎo)出少數(shù)幾個(gè)主成分，使它們盡可能多地保留原始變量的信息，且彼此間互不相關(guān)。通常數(shù)學(xué)上的處理就是將原來P個(gè)指標(biāo)作線性組合，作為新的綜合指標(biāo)[5]。

最經(jīng)典的做法就是用F1（選取的第一個(gè)線性組合，即第一個(gè)綜合指標(biāo)）的方差來表達(dá)，即Var(F1)越大，表示F1包含的信息越多。因此在所有的線性組合中選取的F1應(yīng)該是方差最大的，故稱F1為第一主成分。如果第一主成分不足以代表原來P個(gè)指標(biāo)的信息，再考慮選取F2即選第二個(gè)線性組合，為了有效地反映原來信息，F(xiàn)1已有的信息就不需要再出現(xiàn)在F2中，用數(shù)學(xué)語言表達(dá)就是要求 cov(F1,F2) = 0，則稱F2為第二主成分，依此類推可以構(gòu)造出第三、第四，…F…，第P個(gè)主成分。

1.2 主成分分析步驟

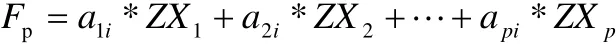
其中 a1i,a2i,… ,api(i = 1, …m)為X的協(xié) 方差陣Σ的 特征值所對(duì)應(yīng)的特征向量， ZX1,Z X2, … ,ZXp是原始變量經(jīng)過標(biāo)準(zhǔn)化處理的值。 A=(aij)p×m=(a1,a2, …am)，Rai=λiai其中，R為 相關(guān)系數(shù)矩陣，a是相應(yīng)的特征值和單位特征向量,λ1≥λ2≥… ≥λp≥0。i

其中主成分分析法的計(jì)算步驟：

（1）指標(biāo)數(shù)據(jù)標(biāo)準(zhǔn)化（SPSS軟件自動(dòng)執(zhí)行）；

（2）指標(biāo)之間的相關(guān)性判定；

（3）確定主成分個(gè)數(shù)m；

（4）主成分Fi表達(dá)式；

（5）主成分Fi命名。

1.3 聚類分析基本思想

依據(jù)研究對(duì)象（樣品或指標(biāo)）的特征，對(duì)其進(jìn)行分類的方法，減少研究對(duì)象的數(shù)目。各類事物缺乏可靠的歷史資料，無法確定共有多少類別，目的是將性質(zhì)相近事物歸入一類。各指標(biāo)之間具有一定的相關(guān)關(guān)系。

主要的步驟如下：第一步：逐個(gè)掃描樣本，每個(gè)樣本依據(jù)其與已掃描過的樣本的距離，被歸為以前的類，或生成一個(gè)新類。第二步，對(duì)第一步中各類依據(jù)類間距離進(jìn)行合并，按一定的標(biāo)準(zhǔn)，停止合并。

2 結(jié)果及其分析

采用SPSS軟件及其R軟件對(duì)新疆工業(yè)各行業(yè)污染的排放量進(jìn)行分析。

2.1 主成分分析

（1）主成分的初始結(jié)果分析

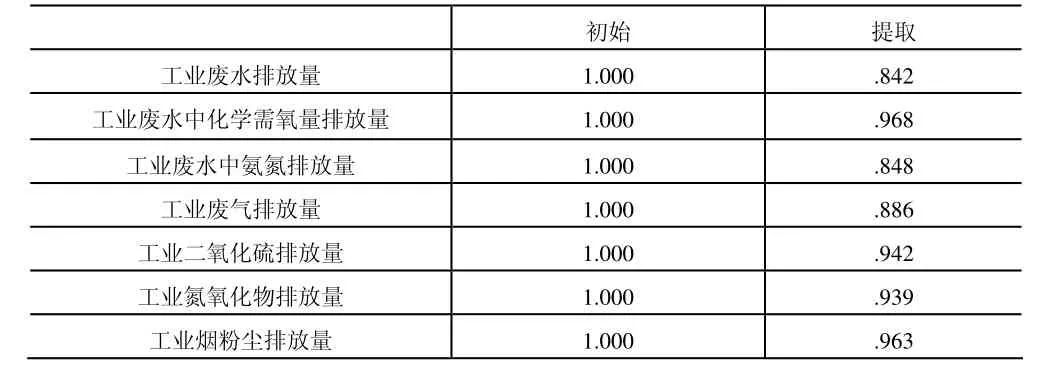
表2 主成分分析的初始結(jié)果

根據(jù)表2可知，主成分包含指標(biāo)變量的信息比較接近，其中指標(biāo)工業(yè)廢水排放量與工業(yè)廢水中氨氮排放量信息損失比較大。

（2）主成分的提取

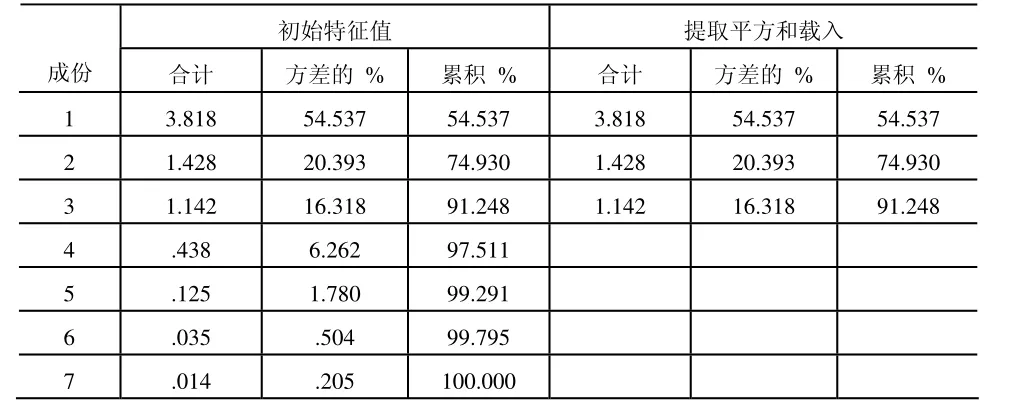
表3 主成分提取表解釋的總方差

觀察表3，主成分提取表中有三個(gè)特征值大于1的主成分，且累積貢獻(xiàn)率達(dá)到91.248%，所以提取三個(gè)主成分比較合適。用碎石圖直觀的表示為圖1：

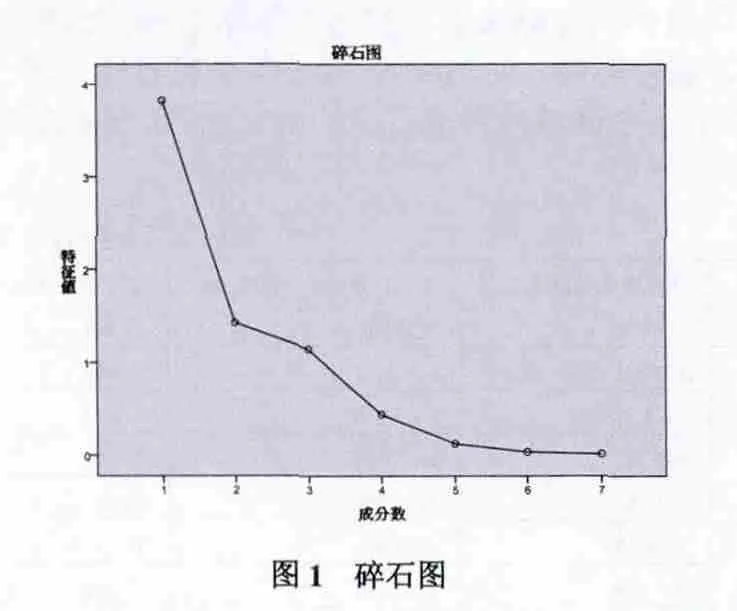
（3）主成分的矩陣表示

把工業(yè)廢水排放量、工業(yè)廢氣排放量、工業(yè)氮氧化物排放量、工業(yè)煙粉塵排放量看作第一主成分，取名工業(yè)污染重要排放物；工業(yè)廢水中化學(xué)需氧量排放量、工業(yè)二氧化硫排放量看作第二主成分，取名第二排放污染；工業(yè)廢水中氨氮排放量看作第三主成分見表4。

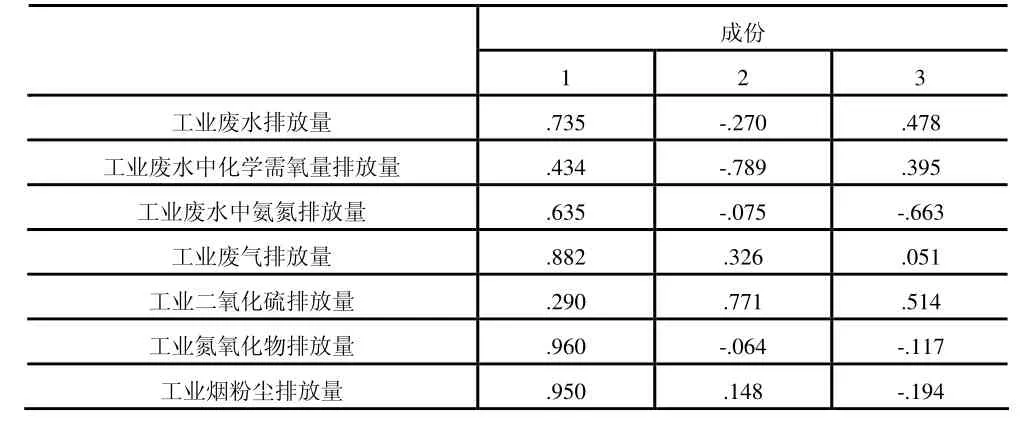
表4 原指標(biāo)變量用主成分表示成份矩陣

（4）主成分的得分

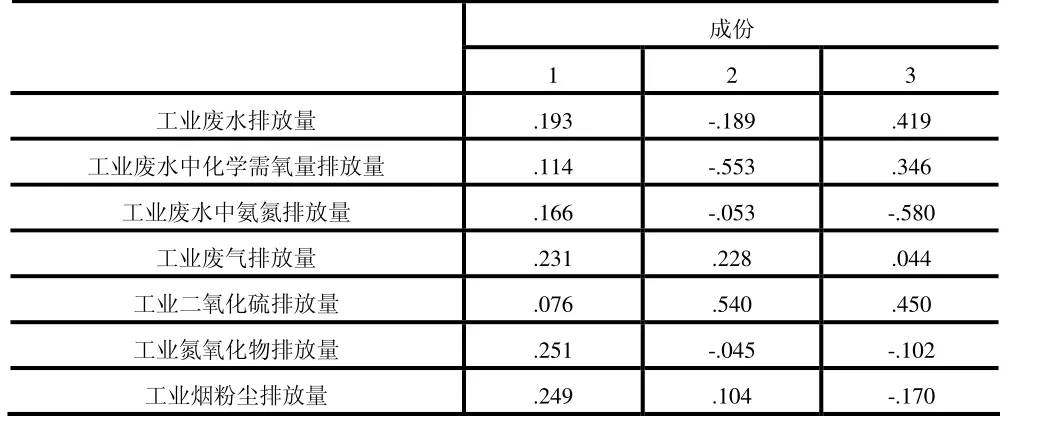
圖5 主成分得分系數(shù)矩陣

則主成分的組合模型公式如下：

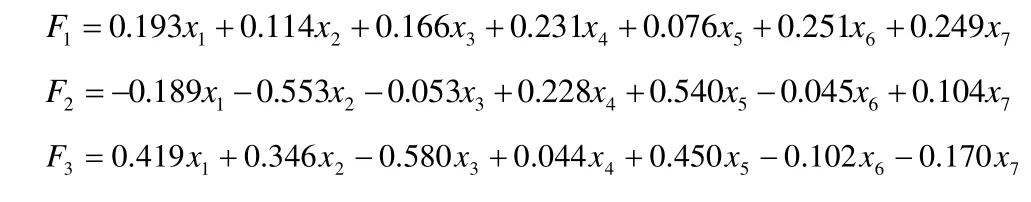
綜合評(píng)價(jià)指數(shù)= 0.55 F1+0.2F2+0.16F3

可以將新疆各個(gè)行業(yè)的工業(yè)廢水排放量、工業(yè)廢水中化學(xué)需氧量排放量、工業(yè)廢水中氨氮排放量、工業(yè)廢氣排放量、工業(yè)二氧化硫排放量、工業(yè)氮氧化物排放量、工業(yè)煙粉塵排放量的截面數(shù)據(jù)分別帶入模型的公式F1，F(xiàn)2，F(xiàn)3中，并計(jì)算綜合評(píng)價(jià)指數(shù)，根據(jù)其得分大小排序，就可以知道哪一個(gè)行業(yè)對(duì)環(huán)境污染的影響最大。綜合得分見表6。

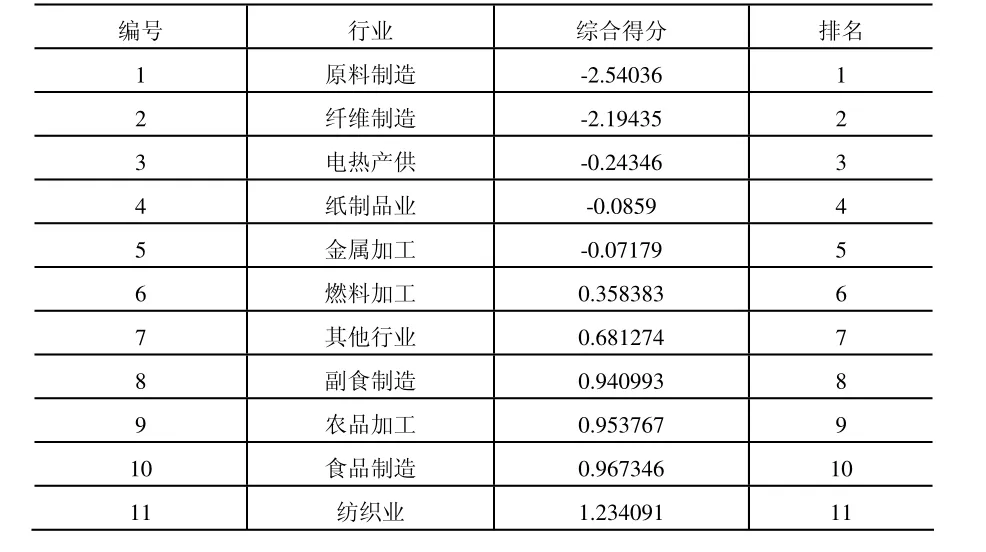
表6 各行業(yè)的綜合得分

根據(jù)綜合得分的表的排名，可知原料制造業(yè)的污染最大，紡織業(yè)的污染相對(duì)來說最小，所以更應(yīng)該加強(qiáng)排名前三的原料制造業(yè)、纖維制造業(yè)、電熱產(chǎn)供業(yè)的治理，這樣才能使環(huán)境越來越好。

表7 主成分的協(xié)方差矩陣

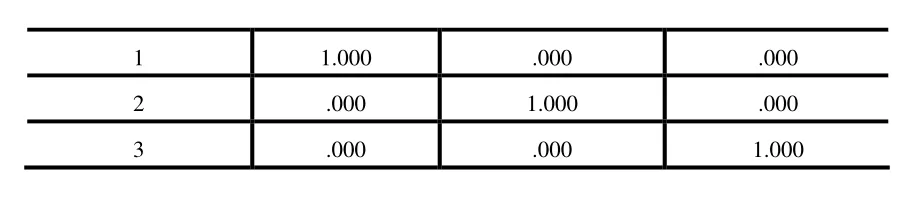
1 1.000 .000 .000 2 .000 1.000 .000 3 .000 .000 1.000

根據(jù)表7可知，三個(gè)主成分兩兩之間的相關(guān)系數(shù)為0，說明經(jīng)主成分分析提取后的三個(gè)主成分之間沒有相關(guān)性，實(shí)現(xiàn)了主成分分析的優(yōu)化設(shè)計(jì)目標(biāo)。

2.2 聚類分析中的層次聚類

用R軟件編程進(jìn)行層次聚類分析，結(jié)果見圖3。

根據(jù)圖3可知將原料制造、纖維制造分為第一類，電熱產(chǎn)供、紙制品業(yè)、金屬加工、其他行業(yè)分為第二類，燃料加工、副食制造、農(nóng)品加工、食品制造、紡織業(yè)分為第三類，采取大致的三類措施進(jìn)行治理，這樣不僅節(jié)約了資金也節(jié)省了時(shí)間。

3 小結(jié)

本文主要是用簡(jiǎn)單的統(tǒng)計(jì)方法得到了原料制造業(yè)、纖維制造業(yè)、電熱產(chǎn)供業(yè)更需要加強(qiáng)對(duì)行業(yè)的管理，雖然其他行業(yè)綜合得分不是很高，但是也不能松懈管理。文章的方法也可以應(yīng)用到各個(gè)省市地區(qū)的各個(gè)行業(yè)，應(yīng)用具有一定的廣泛性。

[1] 李波,肖歡.1991～2011年甘肅省經(jīng)濟(jì)增長(zhǎng)環(huán)境污染研究[J].現(xiàn)代商貿(mào)工業(yè),2013(19):51-53.

[2] 王家庭.我國區(qū)域城市化與環(huán)境污染關(guān)系的空間計(jì)量研究[J].文明和諧與共同繁榮,2013:383.

[3] 閆麗霞.河南省產(chǎn)業(yè)結(jié)構(gòu)升級(jí)與環(huán)境污染關(guān)系研究[J].低碳經(jīng)濟(jì),2013(8):26-29.

[4] 新疆維吾爾自治區(qū)統(tǒng)計(jì)局.2013年新疆統(tǒng)計(jì)年鑒[M].中國統(tǒng)計(jì)出版社,2013.

[5] Richard A. Johnson,Dean W. Wichern. 實(shí)用多元統(tǒng)計(jì)分析(第四版)[M].清華大學(xué)出版社,2001.