北印度洋海浪背景誤差分析和同化預報初步評估

曹蕾，齊鵬

(1.中國科學院海洋研究所，山東 青島266071；2.中國科學院海洋環流與波動重點實驗室，山東青島266071；3.中國科學院大學，北京100049)

1 引言

目前衛星高度計測量技術使我們能夠獲得密集的和覆蓋全球的海面波高信息。長期積累的高度計有效波高資料可用于進行海浪場特征分析，實時的高度計資料為海浪同化的業務化運行提供必要條件。長期以來海浪數值預報精度的提高受限于強迫風場的精度和模式物理過程的不完善，高度計有效波高數據同化成為改進海浪預報的手段之一，得到越來越多的重視。

同化技術中，除同化方法外，背景誤差協方差的準確表達也是重要的研究問題。背景誤差定義為模式預報相對于未知的“真值”之差。由于“真值”不可得到，我們必須尋找其它方法近似地表達和計算背景誤差。常用的求解背景誤差性質的方法主要有觀測法[1]、NMC法[2-3]和集合法等。觀測法將觀測值與預報值之差作為背景誤差的近似；NMC法以同一時刻不同時效的預報值之差作為背景誤差最佳估計；集合法利用長期資料序列組成樣本統計得到背景誤差。后兩種方法是通過尋找能體現背景誤差特征的最佳估計樣本，從統計學角度描述其特征。例如，Greenslade 和Young[4]指出，NMC 法考慮背景誤差增長的預報發散分量。而集合法依賴于集合樣本的選取。

觀測法由Hollingsworth 和L?nnberg[1]提出用于研究背景誤差，可直接確定背景誤差的空間結構。目前采用觀測法對背景誤差協方差進行的研究中，多采用在背景誤差方差為常數的假設下以經驗公式描述背景誤差間的相關系數來替代。Lionello等[5]最早用各向同性且均勻的指數函數來描述背景誤差相關系數，并且認為在45°N緯度帶上相關長度為15°。之后Mastenbroek 等[6]用自回歸函數來描述北海和挪威海的背景誤差結構。Breivik和Reistad[7]也提出新的經驗函數，Voorrips等[8]提出描述波浪總能量誤差結構的經驗函數，Hasselmann 等[9]通過采用Lionello 等[5]的公式同化風場來達到改進海浪的目的，Dunlap 等[10]直接通過一個指數函數將觀測作用在影響范圍內，根據風浪涌浪調節影響范圍。Breivik等[11]在Breivik和Reistad[7]的基礎上使相關長度隨波浪頻率變化。不僅經驗函數多種多樣，同一經驗公式應用于不同海域背景誤差相關長度的設置也不同。例如Bender和Glowacki[12]將Lionello等[5]應用于澳大利亞海域，其相關長度設置為350 km，遠小于45°N緯度帶上的15°。而采用相同經驗函數應用于沿岸海域的研究則相關長度設置相近[7,13-14]。經驗公式的不同表明背景誤差相關系數具有不同的空間結構，同一經驗公式的相關長度不同表明相關性隨距離的衰減速度各異。Greenslade 和Young[15]檢驗了6 種模擬背景誤差相關系數的曲線公式，最終認為Mastenbroek 等[6]對距離較近的結構模擬較好，而Lionello 等[5]對距離較遠的結構模擬效果好；采用觀測法得到背景誤差相關長度尺度在全球分布變化顯著地隨緯度分布具有規律性，隨時間變化則不顯著；相反，背景誤差方差存在相當大的季節和年際變化；對上行和下行軌道分別討論，發現背景誤差協方差在空間上為各向異性。

本文基于觀測法結合Jason-1 衛星高度計沿軌有效波高觀測數據和WaveWatch III海浪模式預報，針對Greenslade 和Young[15]中的5 種較優的曲線做進一步討論，并對擬合過程進行改進，得到該海域背景誤差方差分布特征，以及對整個北印度洋海域而言更為適用的背景誤差相關系數描述公式和對應參數，并分析背景誤差相關長度空間分布的原因。在此基礎上，提出能在大范圍上提高業務海浪預報精度的高度計沿軌有效波高數據最優插值同化方案。

2 模式和數據

本文以15°S—30°N，30°—120°E為目標研究區域。模式預報有效波高即背景場是由第三代海浪模式WaveWatch III 在強迫風場下生成。風場來自于美國國家大氣研究中心（NCAR）的計算與信息系統實驗室（CISL）提供的交叉矯正多平臺（CCMP）海面風場數據集，時空分辨率分別為6 h和1/4°×1/4°。模式采用全球與目標區域雙向嵌套的方案，目標區域的空間網格分辨率為1/4°×1/4°。

根據觀測法進行背景誤差特征分析所采用的觀測資料為2002—2011年OSTM/Jason-1 高度計沿軌有效波高數據。觀測法要求在追求足夠多的采樣點的同時不同觀測站點間的觀測數據是近乎同步的。對Jason-1 資料，相鄰兩條上/下行軌道約間隔1.87 h，相交的上行和下行軌道約間隔12 h。若近似相鄰兩條平行軌道同步，兩軌間距離在赤道上為28.3465°，隨緯度增加間距減小，仍超過北印度洋海域各向同性假設下的相關長度（相較于Greenslade 和Young[15]的500—600 km）。本文僅考慮同一條軌道上更新量之間的相關性，以長時間序列統計的樣本值分析在季節時間尺度上的方差特征。軌道重復時軌跡存在偏差，因此不同時間的同一軌道需要進一步統一位置。

在海浪同化和預報檢驗過程中，Jason-1 和Jason-2衛星高度計資料被用作同化中的觀測資料，本文對質量控制之后的Jason-1和Jason-2觀測數據進行隔點采樣作為用于同化的觀測。而質量控制后的ENVISAT衛星資料作為用于檢驗的觀測。

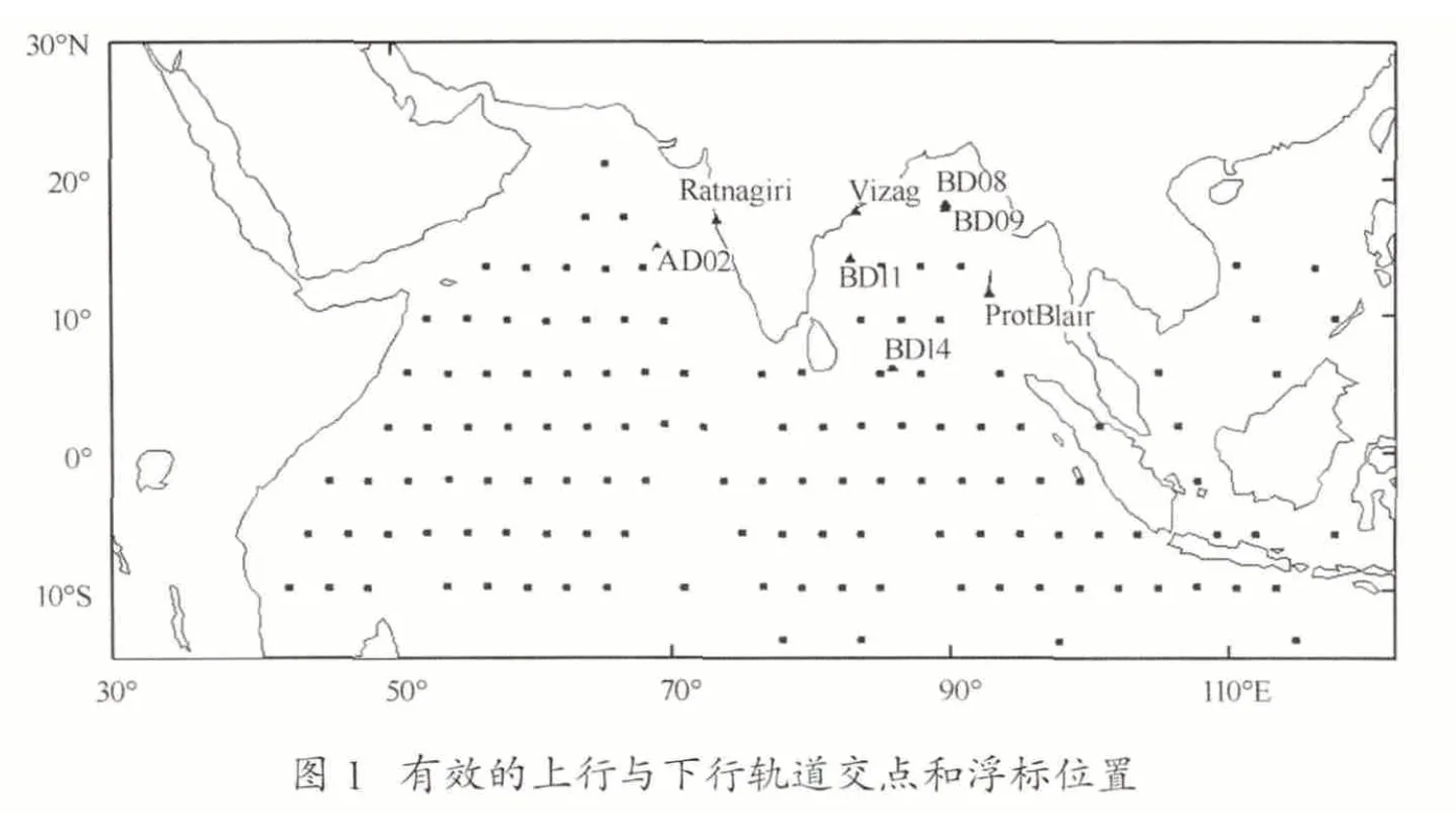
受限于我們缺乏北印度洋海域有效波高浮標觀測，這里我們采用印度國家海洋信息服務中心（Indian National Center For Ocean Information Services）網絡平臺發布的浮標觀測結果圖（浮標位置見圖1），從中提取觀測值和對應時間，得到浮標觀測，讀數誤差小于0.02 m。

在同化應用中，研制了嵌入WaveWatch III version3.14 的最優插值同化模塊，以及為了匹配全球與印度洋目標區域雙向嵌套而自主添加的同化接口，使得雙向嵌套和同化技術能夠同時使用。

3 方法與實驗設計

3.1 觀測法分析背景誤差及其協方差

采用觀測法求解背景誤差特征是本文的主要內容之一。首先求解觀測數據與背景數據之間的總偏差，稱之為更新量。假設預報誤差和觀測誤差無偏以及觀測誤差與背景誤差不相關，得到在觀測點上的更新量方差等于背景誤差方差與觀測誤差方差之和，而兩個觀測點之間的更新量協方差等于背景誤差的協方差，由此通過假設背景誤差相關系數外推擬合曲線在兩個觀測點重合時的值為背景誤差方差與更新量方差之比，分解得到背景誤差方差和觀測誤差方差。

進一步假設背景誤差是各向同性的，相關系數僅與距離有關而與方向無關。求解給定點與經過該點的上行和下行軌道上其它點的相關系數，這里給定點指的是上行軌道和下行軌道的交點（見圖1）。將相關系數僅表示為隨距離的函數。以0—100 km 范圍的平均相關系數當作是0 km 處的相關系數的近似，即背景誤差方差與更新量方差之比，稱為R0。這里選擇這樣的近似來求解R0，而不是采用曲線擬合得到的解析函數外推距給定點距離r為0處的值[15]，是因為擬合時受尾部（即r很大）觀測點的影響，頭部（r接近0處）的模擬不是很理想。之后分解得到背景誤差和觀測誤差，采用三角形內插法插值到網格點上。

由上可以得到每個給定點上觀測誤差方差和背景誤差方差，接下來分析背景誤差之間的相關關系。在各向同性假設下，兩點之間的誤差相關性與兩點的絕對位置和相對位置無關，只與兩點之間的球面距離有關。將所得上/下行軌道上的相關系數表示為隨距離的函數，并采用曲線擬合得到上/下行軌道的解析函數。本文對Greenslade 和Young[15]中選出的5 種經驗函數進行討論（已排除一種趨勢不一致的函數），挑選適用于目標海域的最優形式，其中曲線1曾在不同海域被認為優于其它擬合公式[4,16]。5種經驗公式如下，

Curve 1[6]:

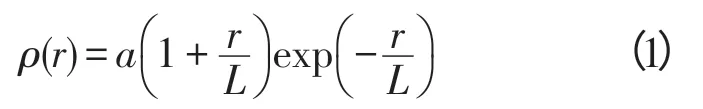
Curve 2:

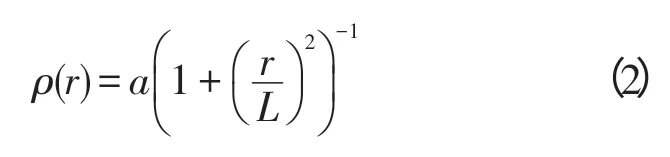
Curve 3:

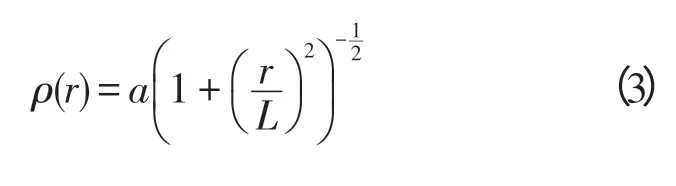
Curve 4[7]:

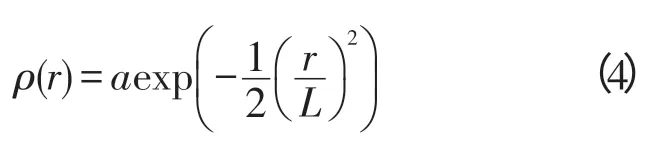
Curve 5[5]:

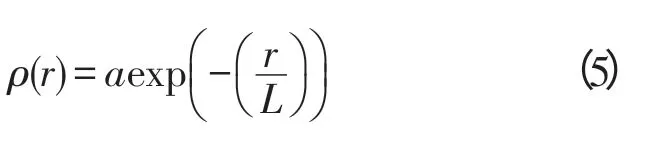
式中，a 為系數，L 為相關長度。系數a 之后的表達式表示點之間的相關性，引入系數a 是因為受到觀測誤差方差的影響，因此a 即為R0。求出背景誤差分別沿上行軌道和下行軌道的相關尺度，記為Lasc和Ldes，取兩者平均值為該給定點上的相關尺度L，之后插值到經緯度網格點上。

3.2 最優插值同化

最優插值同化技術最早廣泛應用于業務化，具有方法較為簡單計算代價較小的優勢，在國內外的海浪同化應用中取得了大量成果[8,9,16-20]。同化過程中，同化窗口的設置會造成觀測值與真值之間的誤差（觀測誤差）含有3 個方面，包含儀器誤差反演誤差環境誤差等等在內的觀測本身的誤差（測量誤差）、用于同化時空間和時間近似產生的時間代表性誤差和空間代表性誤差。如果只考慮同化時刻前后半小時內的沿軌數據，則不存在空間代表性誤差，同時可忽略時間代表性誤差。本文認為不同點上的觀測不相關，利用觀測誤差計算觀測誤差協方差R，這樣R 為對角陣，對角線上元素為觀測誤差方差。目標區域有效波高普遍小于5 m，因此將觀測誤差標準差設為0.12 m。當目標區域是一個空間尺度較大的區域時，雖然背景誤差協方差結構和對應的相關參數存在空間變化，但對于典型的最優插值同化方案，仍假設該目標海域滿足同一種背景誤差協方差結構以及對應的相關參數為常數。本文分別考慮以上討論的經驗公式來描述背景誤差協方差結構。最優插值同化方案中背景場誤差協方差矩陣大多由經驗公式給定，基本結構為：

式中，ρij表示空間兩點i,j 間的誤差相關函數。是背景誤差的方差。根據假定，不考慮σb的空間變化，即σb為常值。σb可以根據觀測法統計結果進行給定，誤差相關函數將分別對5 種曲線進行討論。另外假設只有影響半徑radius內的點與給定點之間才存在相關。

WaveWatch III 是通過對海浪譜計算進行預報的全譜空間海浪模式，同化模塊中的同化對象是有效波高，本文重構海浪譜時僅考慮分析波高改進對海浪譜能量的調整[21-23]。

4 結果

4.1 背景誤差特征

2002—2011年北印度洋海域更新量的總體平均值為-0.23 m，觀測誤差無偏所以背景誤差的平均值為-0.23 m，說明模式預報值平均高估了海浪場0.23 m。偏差的季節分布為冬季-0.07 m，春季-0.27 m，夏季-0.41 m，秋季-0.17 m。此處采用的季節劃分為1—3月為冬季，4—6月為春季，7—9月為夏季，10—12月為秋季。

由觀測法得到的觀測誤差方差量值在0—0.04 m2，整個海域全年平均為0.01 m2，均方根誤差為0.1 m。根據Jason-1產品手冊[24]，偏差矯正之后Jason-1的有效波高測量精度為0.4 m 或10%（以較大者為準）。本文結果僅為該量值的1/4，主要是因為進行了數據質量控制、限定了研究區域以及僅考慮軌道交點。其中質量控制使觀測偏差很大的數據被剔除；觀測誤差相比于南半球風速大的海域，北印度洋海域平均有效波高小，海況好高度計反演精度高。所以相比于手冊中全球結果本文所得觀測誤差偏小，這一現象是合理的。

背景誤差方差分布總體上冬季最小，夏季最大，春秋兩季過渡的性質（見圖2），年平均背景誤差方差為0.107 m2，年平均均方根誤差達到0.327 m。

冬季背景誤差方差均值為0.068 m2。南海海域中部存在一個相對高值區，受冬季風影響形成。出現在安達曼海至印度尼西亞附近以及馬達加斯加島以北海域的高值區，主要的形成原因為模式分辨率低無法體現地形的復雜變化，使得模式模擬有效波高誤差較大，這一現象幾乎全年存在。春季背景誤差方差較冬季增長明顯，全海域平均值為0.12 m2，赤道以南和南海海域出現高值區。夏季背景誤差方差平均值為0.17 m2。赤道以南高值區進一步向北擴張和南海南部海域高值區向南推進。南海南部海域的背景誤差方差減小，但赤道以南明顯增大。考慮到赤道以南海域在夏季的偏差明顯高于其他季節，且冬季預報偏差最小，因此我們認為方差呈現如此季節變化的原因是由于夏季對涌浪預報的過高估計。秋季背景誤差方差迅速減小，全海域平均值為0.07 m2。整個目標海域背景誤差方差迅速減小，除南海海域外其他海域的高值區消失，南海海域高值區向印尼群島收縮。背景誤差方差比觀測誤差方差大了一個量級且變化更為明顯。

表1 是分別按擬合公式1—5 進行擬合得到的全年和整個目標海域時空平均的相關長度。其中曲線5擬合所得總殘差平方和最小，曲線3次之，說明這兩種經驗公式最能體現背景誤差的相關性。

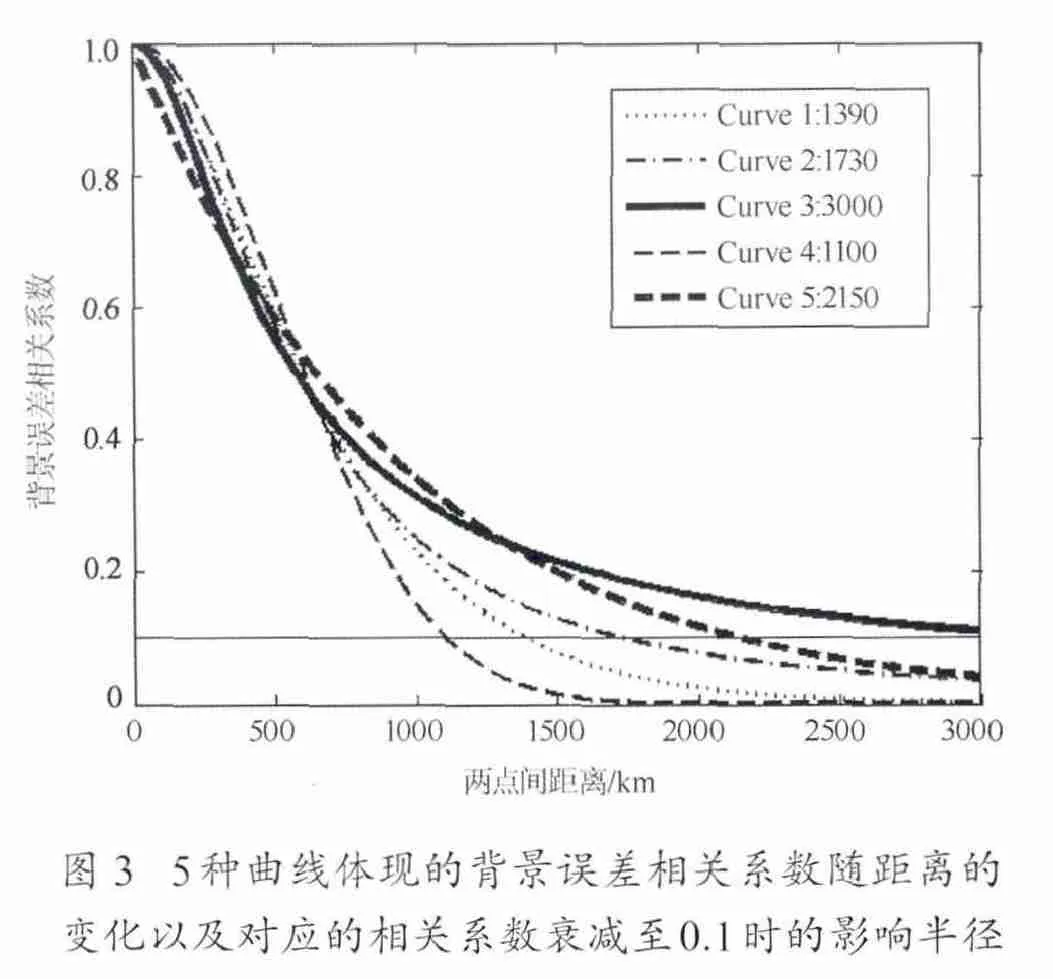
這5種曲線所體現的相關系數隨距離的變化趨勢不相同。曲線3和5與相關系數散點分布擬合較好，尤其是當尾部較長時。觀察發現當距離給定點很遠時，相關系數不是趨于0，而是維持在0—0.2之間或者極其緩慢的衰減至0，曲線3和5也能較好體現這一特征。與之相比，雖然曲線1、2、4 也同樣與相關數據散點分布擬合較好，但是對于長距離的相關系數擬合則趨近于0。不同曲線隨距離衰減程度不同（見圖3），其中曲線4 衰減最快，曲線3 衰減最慢直至3000 km時才小于0.1，后者表示與給定點相關的點的范圍很大，卻多為弱相關。

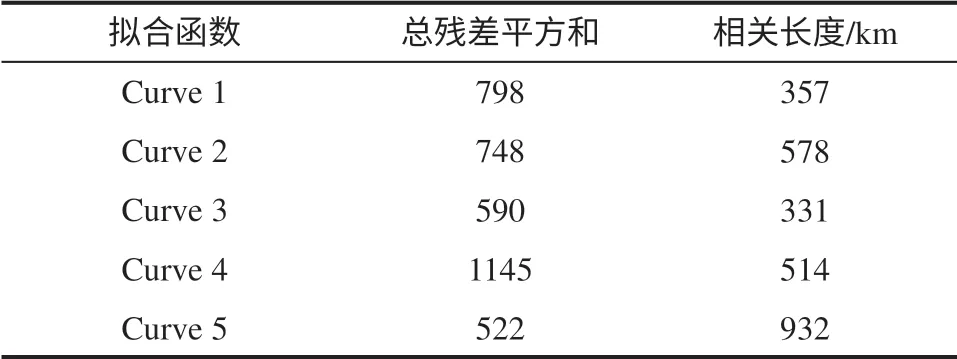
表1 根據曲線1—5擬合得到4個季節整個目標海域時空平均后的相關長度

比較不同擬合公式所得相關長度，發現無論是上行軌道、下行軌道還是兩者平均，相關性都大于0.82 甚至高達0.99，說明不同擬合公式所得相關長度的空間分布趨勢和季節變化趨勢相似。因此以下僅選取曲線3結果作為代表分析相關長度的時空變化（見圖4）。北印度洋海域相關長度尺度冬季整體最小，春夏季節最大。冬季，相關長度尺度量值在100—300 km，僅在冬季風強盛的南海南部海域存在相對高值區（大于300 km）。夏季，相關長度尺度量值大于200 km，最大超過600 km，大值區在北印度洋海域東南部，為涌浪盛行海域。春季分布與夏季相同，秋季呈現過渡趨勢。如果對幾個季節分別進行空間平均，則得到冬季、春季、夏季和秋季的相關長度均值分別為231 km、396 km、373 km 以及322 km。

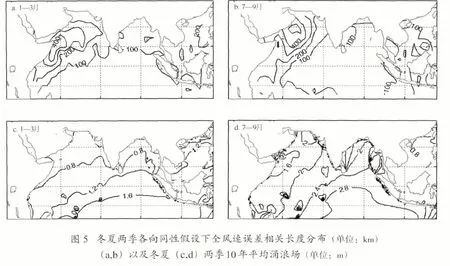
探討導致背景誤差相關長度分布的原因，我們所能想到的是風場對海浪場的影響和傳入涌浪的影響。以夏季為例，對CCMP 風場用觀測法和Jason-1 高度計風場資料求出以全風速表達的誤差相關長度分布和模式模擬的10年平均的涌浪場，我們發現各向同性假設下的相關長度（見圖4）在索馬里以東海域低而在目標海域東南部高，對應季節風場相關性（見圖5）卻在阿拉伯海域高其余海域低。整個目標海域而言，前者分布趨勢西北低而東南高，后者西北高而東南低趨勢相反，而與平均涌浪場的分布形勢（見圖5）相似，其中涌浪是利用模式計算有效波高反演的能量和風浪能量占總能量比例求得的。導致上述分布特征可能的原因是，有效波高中含有的能量是風浪能量和涌浪能量兩部分之和，涌浪時空變化小，有效波高中含有的涌浪信號大范圍內較穩定，使得最后有效波高的相關性分布與涌浪分布相似。以冬季為例，各向同性假設下的有效波高背景誤差相關長度和風場誤差相關長度在索馬里以東海域同時出現高值中心，涌浪作用相對減小但仍然影響北印度洋東部海域。

根據觀測法結果發現兩點之間距離很大時，相關系數介于0—0.2 或及其緩慢的衰減至0，這是由什么引起的？首先我們假設是由觀測誤差引起的。采用更新量求解觀測點之間的協方差，雖然在求解背景誤差方差和觀測誤差方差時可以將兩者分離，但是就誤差而言，雖然觀測誤差比背景誤差小了一個量級，但無法從更新量中消除。但Janssen等[25]認為觀測之間的相關距離為70 km，這個尺度相對于現有的背景誤差相關性尺度很小。所以本文認為尾部持續的弱相關性不是觀測誤差引起的。根據上文分析有效波高中含有的涌浪信號大范圍內較穩定，這里猜想這種弱相關是由于涌浪場造成的。

觀測法的研究結果可以為北印度洋海域海浪同化參數設置提供參考。北印度洋海域Jason-1 衛星高度計有效波高沿軌數據的觀測誤差可以近似認為是0.1 m，但是考慮到參與計算的軌道數據經過質量控制且僅為軌道交點，這一結果偏小。平均背景均方根誤差可以取0.33 m。最優插值同化方案中Jason-1和Jason-2的觀測誤差都采用Jason-2手冊[26]中的GDR-Actual 參數0.12 m。如果采用最優插值或統計插值同化方法，背景誤差協方差的描述函數可以選取曲線3或者曲線5，相關長度可以分別設置為330 km和930 km，但是這兩種擬合公式的影響半徑的設置可能會略有些大，使得大量與給定點距離較遠的點也存在弱的相關。此外，曲線1、2 和4 也是不錯的選擇，對背景誤差協方差的描述形勢一致也保證了相關性隨距離的快速向零靠攏。海浪同化中的背景誤差協方差描述函數的使用將在4.2節進一步討論。

4.2 同化應用

分別采用曲線1—5 作為北印度洋海域背景誤差協方差的描述函數，應用到海浪同化實驗中，以考察實際應用中的最優曲線。應用最優插值技術將Jason-1 和Jason-2 高度計數據同化到海浪模擬中，并用浮標資料進行檢驗。實驗中，背景誤差方差設為0.332m2，觀測誤差方差設為0.122m2。表2為2011年7月采用浮標數據以平均相對誤差改進量形式顯示的同化較無同化模擬的改進效果。容易看出，同化模擬的平均相對誤差較無同化情形的絕對改進量都比較明顯；各浮標站處的改進量對于不同背景誤差協方差描述函數而言均十分接近。采用另一套獨立的資料——ENVISAT 觀測資料對該月的模擬結果進行檢驗，結果顯示該月整個目標海域同化模擬的平均相對誤差較無同化情形的改進量約達10%，不同曲線之間結果的差別均小于0.6%。這表明，在實際應用中，對不同經驗公式給以合理參數，它們的同化改進效果差別甚小，這暗示4.1節擬合曲線中的長距離弱相關性在實際同化計算中影響很小。選取圖3中隨距離衰減較快的曲線4作為以下最優插值同化方案中背景誤差相關系數的描述函數。

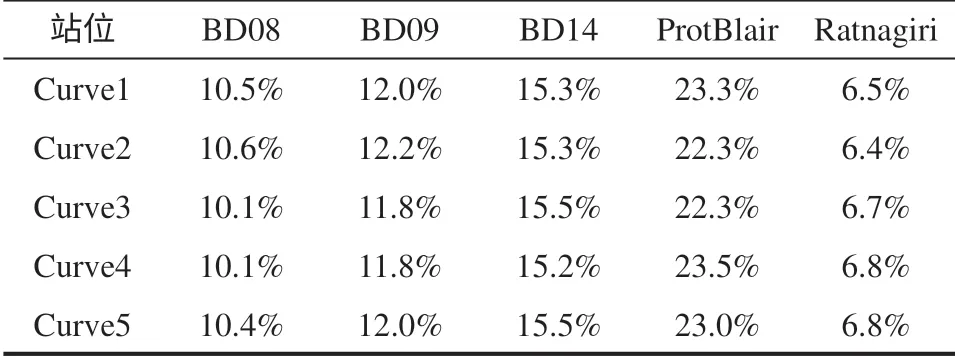
表2 同化結果與浮標資料的平均相對誤差（百分數）較無同化情形的絕對改進量

采用全球-北印度洋海域嵌套設置，分別以NCEP（National Centers for Environmental Prediction）提供的GFS（Global Forecast System）全球模式預報風場和國家海洋環境預報中心提供的WRF（Weather and Research Forecasting model）北印度洋模式預報風場為強迫場，以1°×1°和1/6°×1/6°為空間分辨率，基于最優插值同化方案，進行2013年1月北印度洋海域海浪場業務預報試驗，同化數據為Jason-1 和Jason-2 高度計沿軌有效波高，采用浮標數據（浮標位置見圖1）進行檢驗。利用浮標數據對2013年1月同化和無同化預報進行了檢驗。表3為同化較無同化預報的絕對改進量。顯然，同化不同時效的海浪預報場得到明顯改進。

5 結論

本文基于觀測法，應用連續10年的Jason-1 衛星高度計沿軌有效波高數據并結合WaveWatch III海浪模式預報結果，得到北印度洋海域海浪場背景誤差方差和各向同性假設下背景誤差相關長度的時空分布特征。結果發現在涌浪強于風浪的海域背景誤差相關長度空間分布與涌浪場分布更相似。在給出的表達背景誤差相關系數的5種經驗公式中，Lionello等[5]提出的經驗函數擬合該海域有效波高背景誤差相關系數時總殘差平方和最小。但實際應用于海浪同化時，如果對不同經驗公式采用合理參數，結果之間的差別甚小。在上述工作的基礎上，采用最優插值方法同化Jason-1 和Jason-2 高度計有效波高數據到海浪模式WaveWatch III，進行同化對海浪短期預報影響的評估。利用浮標數據對2013年1月北印度洋海域海浪業務化預報數值試驗進行檢驗，表明同化使24 h預報改進明顯。

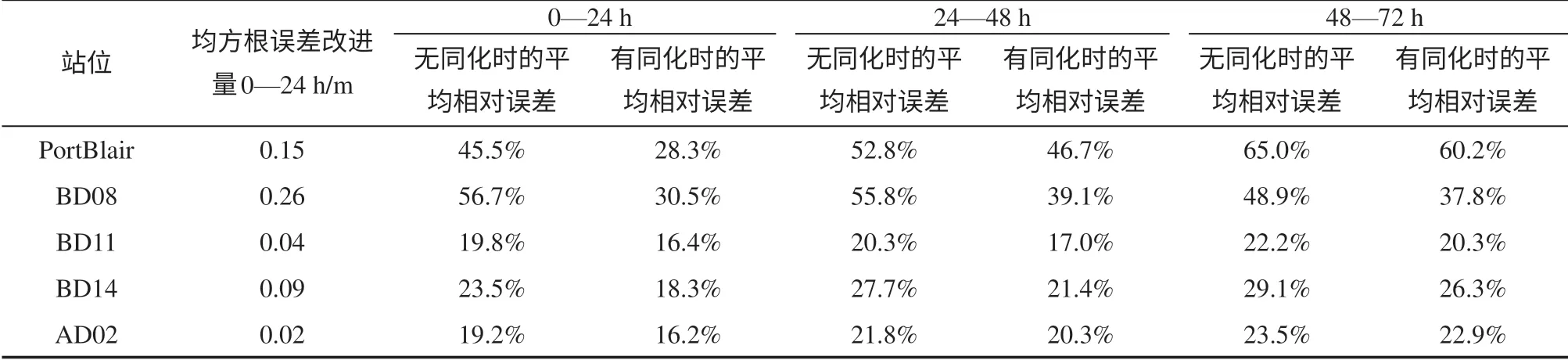
表3 浮標數據對同化預報結果的檢驗

致謝：在本文海浪模式方面得到國家海洋環境預報中心海浪組王毅副研究員的熱情指導，在此致以誠摯謝意。

[1]Hollingsworth A, L?nnberg P. The statistical structure of shortrange forecast errors as determined from radiosonde data. Part I:The wind field[J].Tellus A,1986,38A(2):111-136.

[2]Parrish D F, Derber J C. The National Meteor- ological Center's spectral statistical- interpolation analysis system[J]. Monthly Weather Review,1992,120(8):1747-1763.

[3]Rabier F, McNally A, Andersson E, et al. The ECMWF implementation of three-dimensional variational assimilation (3DVar). II: Structure functions[J]. Quarterly Journal of the Royal Meteorological Society,1998,124(550):1809-1829.

[4]Greenslade D J M, Young I R. Forecast diver- gences of a global wave model[J]. Monthly Weather Review, 2005, 133(8): 2148-2162.

[5]Lionello P,Günther H,Janssen P A E M.Assimi-lation of altimeter data in a global third- generation wave model[J]. Journal of Geophysical Research,1992,97(C9):14453-14474.

[6]Mastenbroek C, Makin V,Voorrips A C, et al.Validation of ERS-1 altimeter wave height measurements and assimilation in a North Sea wave model[J]. The Global Atmosphere-Ocean System, 1994,2:143-161.

[7]Breivik L A, Reistad M. Assimilation of ERS-1 altimeter wave heights in an operational numerical wave model[J]. Weather and Forecasting,1994,9(3):440-451.

[8]Voorrips A C, Makin V K, Hasselmann S. Assimilation of wave spectra from pitch-and-roll buoys in a North Sea wave model[J].Journal of Geophysical Research,1997,102(C3):5829-5849.

[9]Hasselmann S, Lionello P, Hasselmann K.An optimal interpolation scheme for the assimilation of spectral wave data[J]. Journal of Geophysical Research,1997,102(C7):15823-15836.

[10]Dunlap E M, Olsen R B, Wilson L, et al. The effect of assimilating ERS-1 fast delivery wave data into the North Atlantic WAM model[J]. Journal of Geophysical Research: Oceans (1978-2012),1998,103(C4):7901-7915.

[11]Breivik L A, Reistad M, Schyberg H, et al. Assimilation of ERS SAR wave spectra in an operational wave model [J]. Journal of Geophysical Research:Oceans(1978-2012),1998,103(C4):7887-7900.

[12]Bender L C,Glowacki T.The assimilation of altimeter data into the Australian wave model[J]. Australian Meteorological Magazine,1996,45(1):41-48.

[13]Young I R, Glowacki T J. Assimilation of altimeter wave height data into a spectral wave model using statistical interpolation[J].Ocean Engineering,1996,23(8):667-689.

[14]Greenslade D J M. The assimilation of ERS-2 significant wave height data in the Australian region[J]. Journal of Marine Systems,2001,28(1-2):141-160.

[15]Greenslade D J M,Young I R.Background errors in a global wave model determined from altimeter data[J]. Journal of Geophysical Research: Oceans (1978- 2012), 2004, 109(C9): doi: 10.1029/2004JC002324.

[16]任啟峰,張杰,尹訓強,等.Envisat ASAR 海浪譜資料的最優插值同化試驗[J].熱帶海洋學報,2010,29(5):17-23.

[17]張志旭,齊義泉,施平,等.最優化插值同化方法在預報南海臺風浪中的應用[J].熱帶海洋學報,2003,22(4):34-41.

[18]郭衍游,侯一筠,楊永增,等.利用WaveWatch Ⅲ建立東中國海區域海浪同化系統[J].高技術通訊,2006,16(10):1092-1096.

[19]王毅,余宙文.衛星高度計波高數據同化對西北太平洋海浪數值預報的影響評估[J].海洋學報,2009,31(6):1-8.

[20]張志旭,齊義泉,施平,等.衛星高度計波高資料的同化試驗分析[J].海洋學報,2003,25(5):21-28.

[21]Esteva D C. Evaluation of preliminary experiments assimilating Seasat significant wave heights into a spectral wave model[J].Journal of Geophysical Research,1988,93(C11):14099-14105.

[22]Bauer E, Hasselmann S, Hasselmann K, et al. Validation and assimilation of Seasat altimeter wave heights using the WAM wave model[J]. Journal of Geophysical Research: Oceans (1978-2012),1992,97(C8):12671-12682.

[23]齊鵬,范秀梅.WAVEWATCH III 同化模塊的建立和檢驗[J].海洋科學,2013,37(10):111-119.

[24]Picot N, Case K, Desai S, et al. AVISO and PODAAC user handbook. IGDR and GDR Jason products[K]. SMM_MU_M5_OP_13184_CN(AVISO)JPL D_21352(PODAAC),2003.

[25]JANSSEN P, ABDALLA S, HERSBACH H, et al. Error estimation of buoy, satellite, and model wave height data [J].Journal of Atmospheric and Oceanic Technology, 2007, 24(9):1665-1677.

[26]Dumont J, Rosmorduc V, Lillibridge L, et al. OSTM/Jason-2 products handbook[K]. CNES: SALP-MU-M-OP-15815-CN,EUMETSAT: EUM/OPS- JAS/MAN/08/0041,JPL: OSTM- 29-1237, NOAA/NESDIS:Polar Series/OSTM J,2011.