決策級融合技術在環渤海地區短期天氣預報中的應用

馬鵬輝，孫立尹，楊燕軍，張劍

（1.海軍海洋水文氣象中心，北京100161；2.中國人民解放軍92727部隊，山西長治046011）

1 引言

近年來天氣氣候預測方法發展較快，目前業務研究中應用較多的主要有：（1）線性回歸方法或相關分析，即尋找一對變量x 和y 之間的關系；（2）自然正交方法及其擴展，即尋找一組變量x1,x2,…,xn之間的相關型[1]；（3）典型相關方法或奇異值分解方法，即尋找一組變量x1,x2,…,xn和另一組變量y1,y2,…,yn之間的線性關系[2]；（4）人工神經網絡方法，是通過模擬人神經元之間反射的相互傳導過程，來模擬大氣這一非線性的復雜系統[3]，即尋找一組變量x1,x2,…,xn和另一組變量y1,y2,…,yn之間的非線性關系；（5）統計降尺度方法，是利用多年的觀測資料建立大尺度氣候狀況和區域氣候要素之間的統計關系，并用獨立的觀測資料檢驗這種關系，最后再把這種關系應用于數值模式輸出的大尺度數值預報產品，產生局地氣候預測[4]。上述方法中，前3種屬線性方法，它們在預測短期氣候變化這種復雜的非線性系統時效果不理想，因為它們只能揭示變量之間的線性關系[5]。人工神經網絡方法是非線性的，自從被引入到非線性特性顯著的氣象預報預測領域以來，已取得一系列研究成果，被看作是最有應用前景的方法[6]，其缺點是不能處理大量的場格點資料，且短樣本資料容易導致非線性不穩定[7]。統計降尺度方法能夠將數值模式輸出的物理意義較好、模擬較準確的數值預報產品應用于統計模式，從而糾正數值模式的系統誤差且不用考慮邊界條件對預測結果的影響；其缺點是需要有足夠的觀測資料來建立統計模式，且不能應用于大尺度氣候要素與區域氣候要素相關不明顯的地區[8-11]。本文嘗試將數據融合技術引入到天氣預測中，通過決策融合來提高現有預測方法的準確率，以尋求改進天氣預測效果的新途徑。

數據融合是對同目標、多來源數據的自動檢驗、聯合、相關、估計的過程，其目的是為了提高自動決策數據分辨率、決策精度和可靠性等[12]。按融合層次可劃分為像素級融合、特征級融合和決策級融合。其中，決策級融合是在多種決策算法的決策基礎上，將其決策結果（中間）作為輸入矢量，應用決策算法將中間決策結果與實際結果再進行多次決策處理。就天氣預報而言，決策級融合就是通過中間決策結果，將大氣環境數據與實際天氣結果進行多次聯系和處理。楊燕軍等[13-15]分別采用線性回歸法、極值剔除法、支持向量機法對環渤海地區3 個區域共26 個站點的單站、區域短期天氣預報進行了研究。本文以這3種方法作為融合算法，利用相同的歷史資料，對環渤海地區短期天氣預報進行融合決策研究，并對預報效果進行了分析。

2 決策級融合模式訓練過程

初級決策的初始輸入矢量（即特征因子組）可表達為：

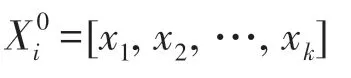
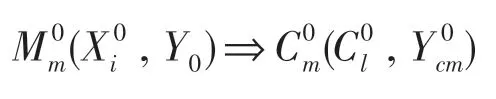
式中，Y0為實際出現的天氣類型代碼組成的矢量；為通過預測方法對進行運算；“ ”表示通過左側的運算得到右側的結果；為與預測方法相對應的預報數據組，其括號內的內容表示預報數據組的具體內容，即初級決策方法的計算系數；為與初級預測方法相對應的預報臨界值，其下標仍為預測方法序號。

則初級決策過程可表達為：

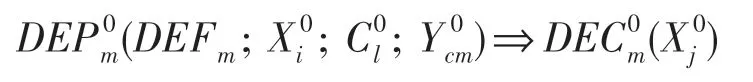
融合決策的實質，就是將中間（含初級）預測結果作為輸入矢量，與預測對象的實際結果再做一次聯系。那么，融合決策的輸入矢量可表達為：

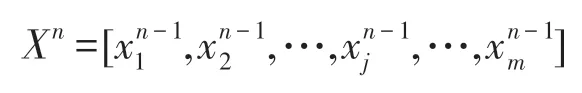
式中，n 表示融合決策級次（即進行n 次融合決策），當n=1 時，其矢量各元素即為初級決策結果。為了與初級決策的數學描述方法一致，這里仍采用分別表示預測方法、計算系數數據組、預報臨界值。那么，不同級別融合決策的模式訓練過程可表達為：

南海北部陸坡深水盆地中早期廣泛發育的水道侵蝕形成了大量的深水水道，而這些深水水道的發育是形成淺水流層的關鍵因素。原本空洞的深水濁積水道會受到區域構造沉降、海平面變化的影響而開始充填巨厚的濁積砂體。而這些砂體會隨著埋深的增加，逐漸被低滲泥巖或頁巖地層所覆蓋，地層載荷也隨之增加，地層間的孔隙流體卻不能有效排出，從而導致在下覆地層中不斷積累，最終形成局部異常超壓環境，這就是淺水流層的形成過程。

……

級決策級融合模式訓練中的預測方法、預報數據組、預報臨界值等代碼的下標為1，表明最后一次融合只采用1種預測方法，得到的結果是1組預報數據和1個預報臨界值。

3 決策級融合的決策過程及決策模式

在經過前述初級和各級融合的模式訓練后，得到初級和各級融合決策的預報數據組和預報臨界值，就可以進行各級融合決策。與前述決策級融合的模式訓練過程相對應的決策過程可以表達為：

……

本文對環渤海地區的天氣預報研究分為3個預報時效，即0—24 h、24—48 h 和48—72 h。其中每個預報時效的決策模式采用兩級決策，即初始決策和一級融合決策。在初始決策中，分別采用線性回歸法、極值剔除法和支持向量機法；在融合決策中，只進行一級融合決策，即m=3，n=1。

表1 各站點平均歷史擬合率一覽表（%）

4 模式訓練效果分析

文獻[13-15]已對預報區域、預報對象（天氣類型）及優先順序、特征因子選擇及篩選等方面的情況作了詳細說明，這里不再贅述。本文首先以線性回歸法為初始決策算法，利用1996—2010年常規氣象資料（其中1996—2005年資料用于模式訓練，2006—2010年資料用于預報模式的試報檢驗），采用歷史擬合率和試報準確率對決策級融合在環渤海地區短期天氣預報中的預報效果進行分析。其中，歷史擬合率從兩個角度進行統計分析。

一是各個站點平均歷史擬合率。表1是環渤海地區3個區域各站點平均歷史擬合率，表中站點序號代表的具體站點見表3。由表1 可知，平均歷史擬合率最高值為91.91%（威海站），最低值為68.48%（寶坻站）。26個站點中，平均歷史擬合率低于70%的站點1 個，占3.84%；高于90%的站點2 個，占7.69%；80%—90%的站點5 個，占19.23%；75%—80%的站點14 個，占53.85%；其余4 個站點的平均歷史擬合率在70%—75%，占15.38%。平均歷史擬合率在75%以上的站點占80.77%。

二是不同預報時效平均歷史擬合率。從各種預報時效平均歷史擬合率一覽表（見表2）可知，平均歷史擬合率隨著預報時效的后延略有降低，但在76%以上。

表2 各預報時效平均歷史擬合率一覽表（%）

試報準確率是按不同站點的各種預報時效來進行統計的。表3 是各預報站點的不同預報時效的試報準確率。相比之下，試報準確率較歷史擬合率低10%左右。其中，達到80%以上的占1.28%，70%—80%的占21.79%，65%—70%的占39.74%，60%—65%的占21.79%，50%—60%的占14.10%。

由以上分析可知，采用線性回歸作為初始決策方法應用于環渤海地區短期天氣預報時，決策級融合獲得了較為理想的歷史擬合率和試報準確率。雖然試報準確率相對較低，但是試報準確率達到65%以上的占64.11%，因此本文認為，決策級融合在環渤海地區短期天氣預報中的應用，具有較好的可信度。

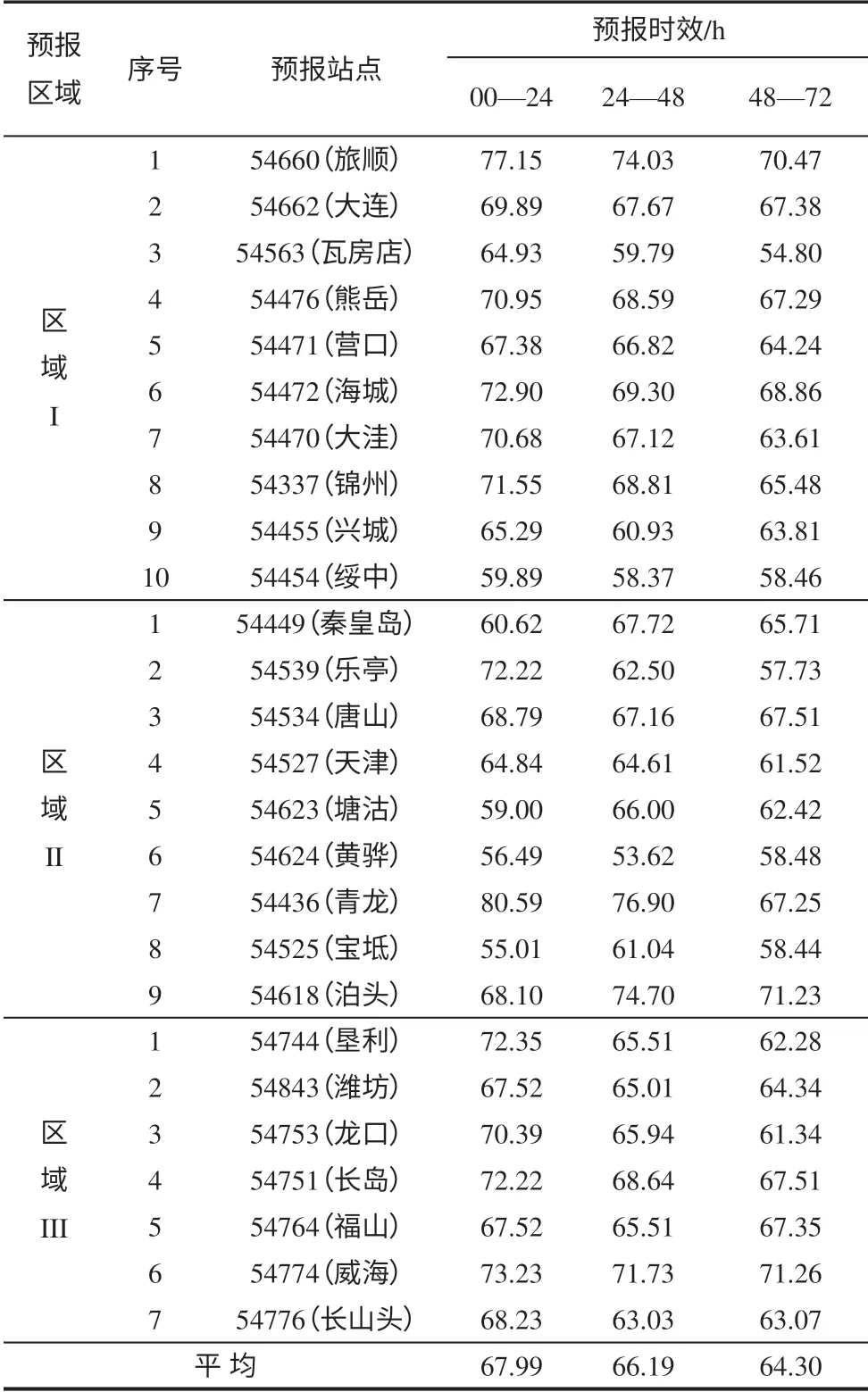
表3 短期天氣預報試報準確率一覽表（%）

5 模式訓練結果比較分析

采用和上述同樣的方法，分別以極值剔除法、支持向量機法作為初始決策方法進行決策級融合，計算不同預報時效的平均歷史擬合率和平均試報準確率（詳細過程略），結果如表4 所示。與楊燕軍等[13-15]得出的初始預報決策平均歷史擬合率和平均試報準確率（見表5）進行比較可知，經過決策級融合后，3種初始決策方法的平均歷史擬合率總體上得到了提升，其中，0—24 h 和24—48 h 的融合決策效果更好一些，平均提升2%—3%，48—72 h 的融合決策結果與初始決策結果相當；3種初始決策方法的平均試報準確率均有所提升，各預報時效平均提升2%左右。上述兩方面的比較結果表明，經過決策級融合后，提高了平均歷史擬合率和試報準確率。

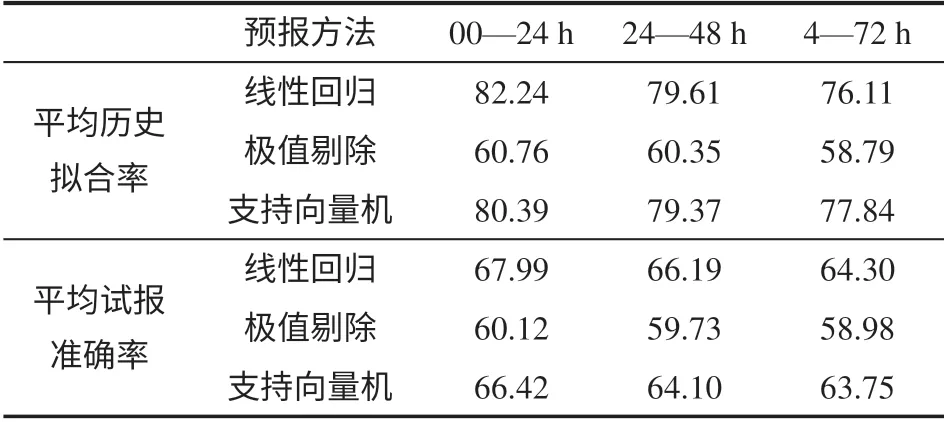
表4 決策級融合的平均歷史擬合率和試報準確率

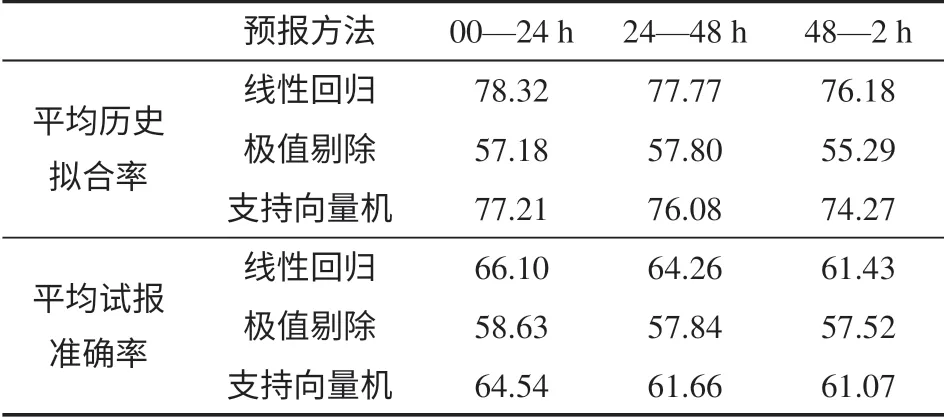
表5 初始決策下的平均歷史擬合率和試報準確率

6 結論

（1）本文以線性回歸法、極值剔除法、支持向量機法為初始決策方法對環渤海地區的短期天氣預報進行了研究。結果表明，預報效果在初級決策的基礎上有所提高，特別是提高了預報結果的可信度；

（2）采用線性回歸作為初始決策方法進行融合決策時，單站短期天氣預報平均歷史擬合率＞75%的站點占80.77%，>70%的站點占96.16%；就預報時效而言，3 個預報時效的歷史擬合率均>76%；就試報準確率而言，試報準確率>65%的站點占64.11%，>60%的站點占85.90%；

（3）無論是平均歷史擬合率還是平均試報準確率，3 種初始決策方法經決策級融合后都有提高，比較而言，0—24 h 和24—48 h 的融合決策效果要好于48—72 h；

（4）決策級融合在環渤海地區短期天氣預報應用的研究結論表明，決策級融合在日常業務預報系統中應用是可行的，可以在預報保障上發揮較好的指導和輔助作用。

[1]張書俊.自然正交分解在降水場預測中的應用[C]//中國氣象學會. 推進氣象科技創新加快氣象事業發展——中國氣象學會2004年年會論文集.北京:氣象出版社,2004:56-60.

[2]張萬誠,鄭建萌,解明恩.典型相關方法在低緯高原汛期降水預報中的應用試驗[J].氣象,2002,28(6):32-34.

[3]董全,黃小玉,宗志平.人工神經網絡法和線性回歸法對降水相態的預報效果對比[J].氣象,2013,39(3):324-332.

[4]劉永和, 郭維棟, 馮錦明, 等. 氣象資料的統計降尺度方法綜述[J].地球科學進展,2011,26(8):837-847.

[5]Hsieh W W, Tang B Y. Applying neural network models to prediction and data analysis in meteorology and oceanography[J].Bulletin of the American Meteorological Society, 1998, 79(6):1855-1870.

[6]朱智慧.BP 神經網絡方法在海浪數值預報中的釋用研究[J].大氣科學研究與應用,2011,21(1):84-91.

[7]胡江林,張禮平,宇如聰.神經網絡模型預報湖北汛期降水量的應用研究[J].氣象學報,2001,59(6):776-783.

[8]Meal L O,Bogardi I,Giorgi F,et al.Comparison of climate change scenarios generated from regional climate model experiments and statistical downscaling[J]. Journal Geophysics Research, 1999, 104(D6):6603-6621.

[9]王冀,宋瑞艷,郭文利.統計降尺度方法在北京月尺度預測中的應用[J].氣象,2011,37(6):693-700.

[10]李江萍,王式功.統計降尺度法在數值預報產品釋用中的應用[J].氣象,2008,34(6):41-45.

[11]任麗娜,翟宇梅,王力維.多模式集合在統計降尺度應用上的研究進展[J].科學技術與工程,2011,11(29):7185-7194.

[12]霍宏濤.數字圖像處理[M].北京:北京理工大學出版社,2002.

[13]楊燕軍.線性回歸方法在環渤海地區天氣預報中的應用[C]//中國海洋學會軍事海洋學專業委員會.第八屆軍事海洋戰略與發展論壇論文集.北京:海潮出版社,2012:156-160.

[14]馬鵬輝,楊燕軍.極值剔除法在環渤海地區天氣預報中的應用[J].航空氣象科技,2011,21(4):17-20.

[15]楊燕軍,馬鵬輝,張劍.基于支持向量機的環渤海地區短期天氣預報[J].導彈氣象,2012,19(3):9-12.