基于規則格網DEM提取坡度坡向的統一模型研究

梁星 賈敦新

(重慶市地理信息中心,重慶 401121)

基于規則格網DEM提取坡度坡向的統一模型研究

梁星 賈敦新

(重慶市地理信息中心,重慶 401121)

本文通過對現有基于DEM的坡度坡向差分算法的分析,提出了基于規則格網DEM提取坡度坡向的統一計算公式,編程實現了算法的統一模型,并成功集成到了ArcGIS產品中,基于本模型可以自定義坡度坡向的計算方法,也可以通過修改參數的方法定制任意一種差分算法獲取地面坡度和坡向,為科研工作者和實際應用者提供了全面有效的計算方法。

數字高程模型 坡度 坡向 統一模型

坡度坡向是相互聯系的兩個參數，坡度反應斜坡的傾斜程度，坡向反應斜坡所面對的方向。作為描述地形特征信息的重要指標，是水文模型、滑坡監測與分析、地表物質運動、土壤侵蝕、土地利用規劃等地學分析模型的重要參數。坡度和坡向與其他參數一起使用，有助于諸如森林蘊藏量估算、水土保持、野生動植物保護、選址分析、土地利用以及其他應用問題的解決。例如，在農業土地開發中，大于25°的坡度一般被認為是不適宜耕種的，而在熱帶經濟作物耕種規劃中，坡向則是評估寒冷凍害風險的重要因子。在實際應用中，某些應用軟件，例如ArcGIS等雖然提供了坡度坡向的計算方法，但是由于不同的用戶在不同的地區針對不同的數據需要采用不同的計算方法，而這些應用軟件就像一個黑箱，只是提供了單一的計算方法，對于用戶而言很難進行選擇和擴展，尤其是科研工作者，在研究不同計算方法對計算結果或者，不同數據誤差對計算結果，或者不同誤差在不同計算方法下的傳播規律時顯得束手無策。如果重新一一編程實現則顯得太過麻煩也不切實際，畢竟用戶和科研工作者關注的不是編程，因此本文針對以上問題，深入分析了基于規則格網DEM的坡度坡向的差分算法，提煉出了不同差分算法的統一模型，并編程實現了該模型，集成到了常用的應用軟件中，極大的方便了廣大科研工作者和實際應用者。

1 坡度坡向的定義

空間曲面的坡度(slope)和坡向(aspect)是互相聯系的兩個參數，均是點位函數，除非曲面是一平面，否則曲面上不同位置的坡度和坡向是不相等的。坡度反映曲面的傾斜程度，定義為曲面上一點P的法線方向與垂直方向(即天頂)Z之間的夾角，而坡向是斜坡面對的方向，定義為P的法線正方向在平面的投影與正北方向的夾角，如圖1所示。

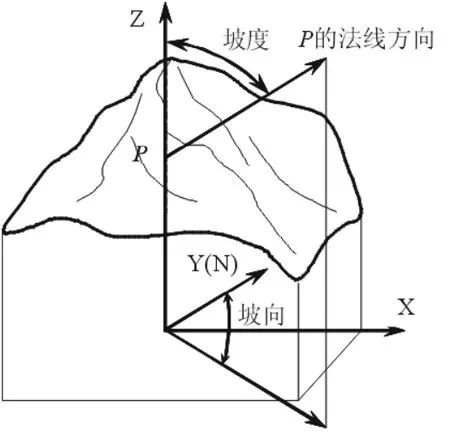
圖1 坡度和坡向定義

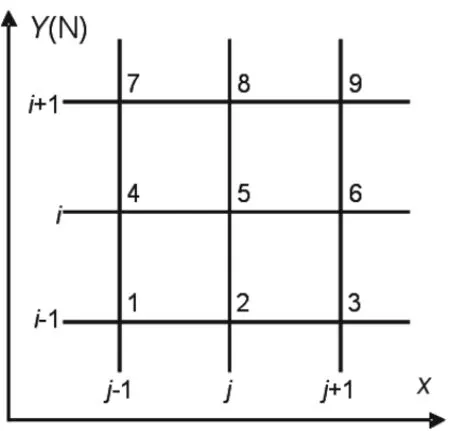
圖2 差分法坡度坡向計算原理

由數學分析知，任一空間曲面 z= f（x, y ）在平面上表示一等值線簇 f（x,y）= c(c為任意常數)， 當z為高程時則為等高線。對任意點P （x ,y ），沿P的梯度反方向，f（x, y）取得其下降最快值。在數字地形分析中，該值即為P的坡度，其下降方向即為坡向或流向。對于函數f（x,y ），P點的梯度表示為：

式中i， j為單位方向，其模(norm)即為坡度(或梯度)，表示為單位長度上的高程升降，通常以百分數表示：

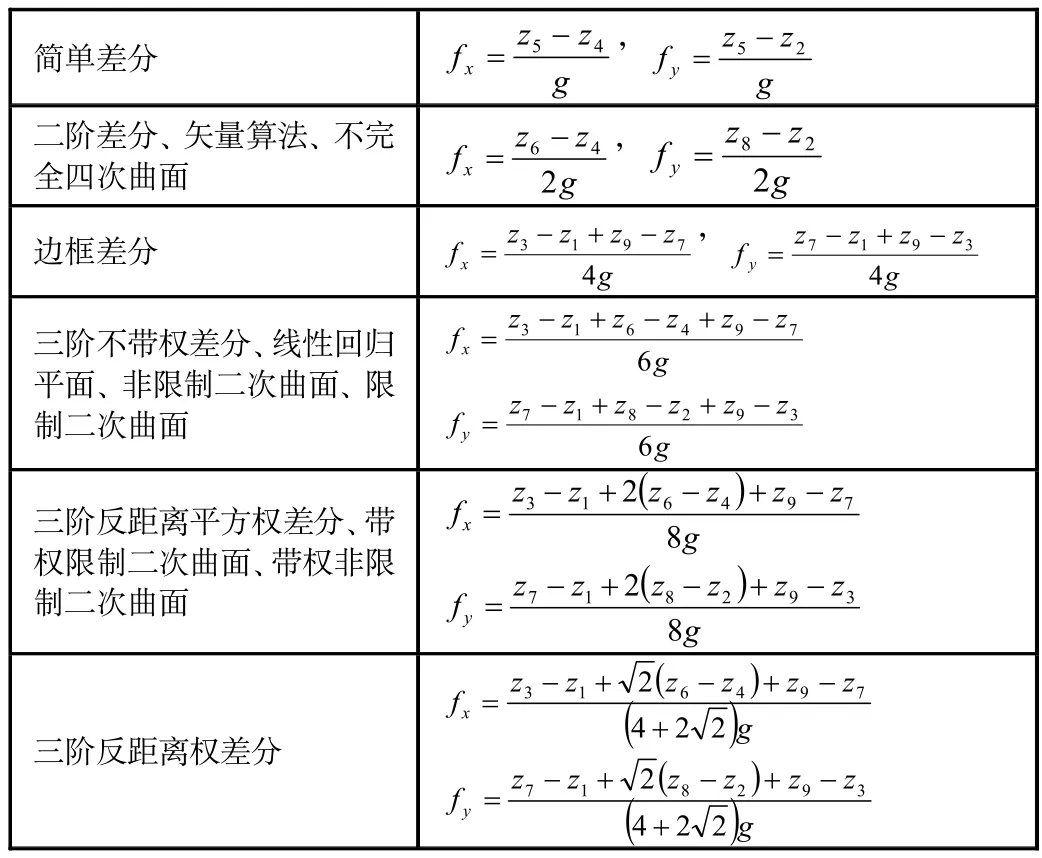
表1 格網DEM坡度坡向計算數學模型

表2 三階反距離平方權差分fx和fy對應權重

圖3 坡度坡向統一模型設計

當需要計算斜坡角度時(即P的法線與天頂Z之間的夾角)，由上式我們有：

當 fy≠0時，梯度方向即為坡向，定義為：

實際工作中，坡向一般以北方向為起始方向，并按順時針方向度量，則坡向在x軸為東西方向、y軸為南北方向(北方向)的坐標系中表示為：

2 基于規則格網DEM提取坡度坡向的統一模型

由上述表達式可知，求解地面某點的坡度和坡向，關鍵是求解fx和fy。DEM是以離散形式表示的地形曲面，而且在多數情況下曲面函數是未知的，因此在DEM上對fx和fy的求解，一般要進行曲面擬合或通過數值微分的方式進行。這里需要注意的是坡度坡向是地形表面的固有屬性，其數學定義是嚴格的，并不隨DEM結構的改變而改變。但由于數字高程模型僅僅是對地形曲面的一種近似，不同的模型結構可能導致不同的坡度坡向計算結果，并且計算方法也隨之而異。鑒于這種考慮，我們將以使用最為廣泛的規則格網DEM進行分析。

在格網DEM上對fx和fy求解，一般是在局部范圍(3×3移動窗口)內，通過給格網點一定編號(中心格網點一般為5)，利用差分原理進行計算。如圖2，設中心格網點為 （i, j ），相應坐標為 （xi, yj），局部地形曲面設為 z= f（x, y ），g為格網間距，則在（i, j）處的泰勒級數展開式為(取至一次項)：

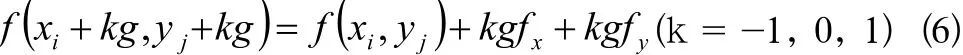
式中k為展開范圍，按不同的k的取值和定權方式，將產生不同的坡度坡向數學模型。表1概括了基于格網DEM的坡度坡向算法和導數計算公式。

3 基于DEM提取坡度坡向統一模型的實現

通過以上所述和表1中的總結，求解地面某點的坡度和坡向，關鍵是求解fx和fy。以圖2為例，若求z5點的坡度或者坡向，則關鍵問題是求解z5點的fx和fy，而求解z5點的fx和fy的關鍵問題是對1-9的賦權問題，以三階反距離平方權差分為例，fx和fy，分對應的權重如表2，因此對fx和fy的求解問題轉化為對待求點周圍9個點的賦權問題，對于其他的差分方法具有相同的規律，因此本文坡度坡向的統一模型設計如圖3，通過選擇不同的差分算法或者輸入不同的權重就可以定制不同的差分算法，進而得到不同算法下的坡度坡向計算結果。本文基于C#和ArcGIS Engine開發實現了本算法，并成功的集成到了ArcGIS桌面產品中，從而更加方便的使用本算法。

4 結語

坡度坡向作為描述地形特征信息的兩個重要指標受誤差的影響很大，尤其是不同的誤差，對于地形數據而言，區分為數據誤差和模型誤差，不同的算法對不同的誤差敏感性不一，這與地形的復雜程度有著很大的關系，因此根據不同的數據，在不同的地區選擇不同的計算方法尤為重要，因此本文將各種差分算法進行了分析，提出了統一的計算模型，并實現了算法，集成到了應用最為廣泛的ArcGIS產品中，對于基于規則格網的DEM的地形分析具有重要的意義。

[1]賈敦新,湯國安,王春.DEM數據誤差與地形描述誤差對坡度精度的影響[J].地球信息科學,2009.

[2]劉學軍.基于規則格網數字高程模型解譯算法誤差分析與評價[D].武漢大學博士論文,2002.

[3]周啟鳴,劉學軍.數字地形分析[M].北京:科學出版社,2006:282-283.

[4]王春,湯國安,張婷 等．在降雨侵蝕中黃土地面坡度變化的高分辨率研究[J].山地學報,2005(5):589-595.

梁星(1982-),男,重慶涪陵人,碩士,現為重慶市地理信息中心工程師,研究方向:地圖學與地理信息系統、遙感。