基于離散元法預測碳化硅陶瓷的高溫力學性能

姜勝強，譚援強，張高峰，彭銳濤

（湘潭大學機械工程學院，湘潭411105）

0 引 言

陶瓷材料由于具有優良的力學性能而被廣泛應用于航天、航空、發動機、機械電子等領域。以碳化硅（SiC）陶瓷為例，因其具有優良的高溫力學性能以及較低的熱膨脹系數、較高的熱導率以及密度小等優點，而被廣泛用于制造火箭發動機燃燒室內壁、噴嘴及鼻錐等重要零件［1-2］。從文獻報道可知［3-5］，近年來諸多研究人員針對陶瓷等結構材料的高溫力學性能進行了大量試驗，雖然獲得了比較可靠的力學性能參數，但試驗周期長，需要消耗大量的人力、物力和財力，且對于具有復雜形狀的陶瓷結構件來說，受試驗條件限制，難以獲得其力學性能參數及高溫破壞機理。

隨著計算機技術及數值分析技術等的飛速發展，采用數值模擬的手段來研究陶瓷材料在不同溫度下力學性能的方法得到了廣泛應用。朱偉等［6］采用分子動力學法模擬了不同溫度下RDX（三亞甲基三硝胺）晶體的力學性能，王超等［7］采用分子動力學法模擬了防熱陶瓷材料的高溫力學性能及斷裂模式。

1971年，Cundall［8］首次提出了適用于巖石力學的離散元法（DEM），目前該方法已在巖石［9］、混凝土［10］和陶瓷［11-13］等材料中得到了廣泛應用。離散元法起源于分子動力學，將材料視為離散顆粒的集合體，顆粒之間用鍵連接，用鍵的斷裂來描述微裂紋的產生，而且模擬過程中溫度具有可控性，從而使離散元法成為模擬陶瓷等脆性材料高溫力學性能及高溫損傷破壞過程的一種新手段。

作者基于離散元法建立并校準了碳化硅陶瓷常溫下的力學性能，并建立了對塊體材料離散化的熱力學模型，將其引入單軸壓縮及三點彎曲等試驗來模擬碳化硅陶瓷在不同溫度下的力學響應，并動態地觀察其損傷破壞過程。

1 離散元模型的建立及校準

離散元中顆粒與顆粒之間的相互作用力由位移重疊量及相應的力-位移準則來確定，顆粒在任意時步內的運動滿足牛頓第二定律。離散元法將裂紋的生成與擴展看成是顆粒與顆粒之間連接鍵的斷裂，能直觀地處理裂紋的形成與擴展過程，如圖1所示。

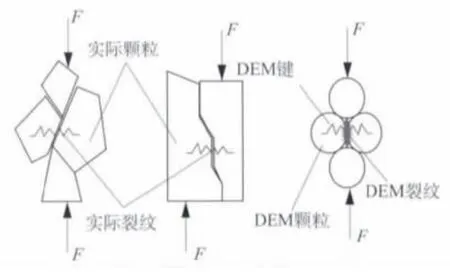
圖1 離散元模型中的裂紋Fig.1 Cracks in DEM model

為了建立與碳化硅陶瓷微觀結構及力學行為相似的離散元模型，采用PFC2D［14］軟件生成一個顆粒隨機分布且緊密排列的顆粒粘結（BPM）模型，顆粒之間采用平行鍵連接。眾所周知，陶瓷材料屬于典型的非勻質體，晶粒尺寸大小不一，且含有隨機分布的氣孔和雜質。為了使離散元模型和實際材料在微觀角度上相似，采用不同尺寸的顆粒來描述晶粒（最大半徑與最小半徑之比為1.5），并使整個模型的孔隙率與材料的孔隙率相符。除此之外，為了使所建立的離散元模型與實際材料的力學性能（如彈性模量、抗壓強度、泊松比等）相匹配，需要對離散元模型中的參數（如顆粒剛度、顆粒之間的摩擦、顆粒之間的鍵強度等）進行反復調試和設置。目前，這些微觀參數很難通過試驗的方法來測試，將陶瓷材料的宏觀力學性能與微觀參數相匹配的方法也還在繼續探索中。因此，采用數字試驗校準的方法對離散元模型進行不同的試驗模擬，以校準模型中的微觀參數。采用單軸壓縮、三點彎曲、單邊切口梁等試驗來校準所建立的碳化硅離散元模型［12］，結果如表1所示。前述力學性能試驗過程中的碳化硅陶瓷通過真空反應燒結工藝制備（碳化硅微粉粒徑8～10μm，反應燒結溫度1 700℃），燒結成型后的材料中含約10%（質量分數）的游離硅，其余為碳化硅。

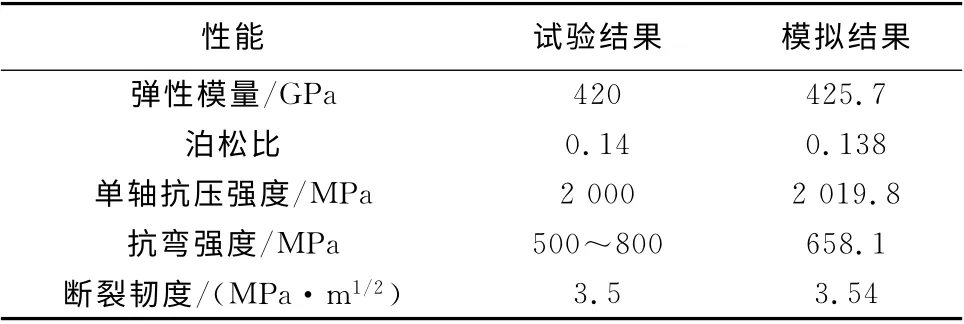
表1 碳化硅陶瓷離散元模擬與實測主要力學性能Tab.1 Main mechanical properties of SiC ceramic in experiment and in DEM simulation

2 離散體中的熱力學模型

2.1 熱傳導方程

在PFC2D 中，采用含有熱存儲器（與顆粒相關）和熱管（與鍵相關）的微觀結構模型來模擬溫度場，熱量在通過熱存儲器之間的激活熱管中傳遞，如圖2所示。熱管與顆粒之間的接觸同時存在，但只有在兩個顆粒之間有重疊或者有連接鍵存在時，熱管才是激活的。如果構成材料的微觀模型在加載過程中有連接鍵產生或者斷裂，都將改變激活熱管的數量，從而改變材料的導熱能力。

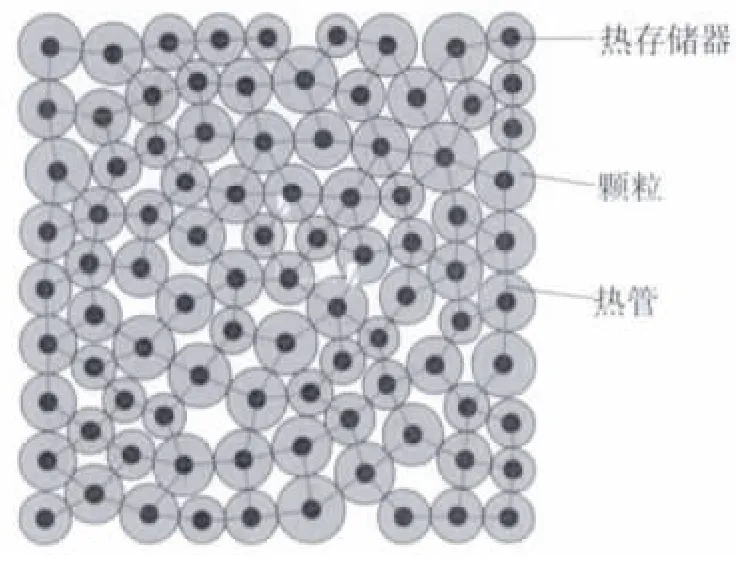
圖2 PFC2D中顆粒、熱存儲器和熱管的示意Fig.2 Abridged general view of particles，thermal reservoirs and heat pipes in PFC2D

對于連續體而言，假定物體應變的改變不會產生溫度的變化，則其熱傳導方程為

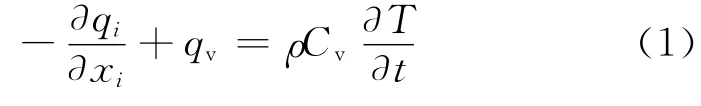
式中：qi為沿坐標軸xi方向的熱流通量；qv為單位體積內的熱功率密度；ρ為質量密度；Cv為材料的比熱容；T 為溫度；t為時間，xi為空間坐標；下標i為方向指標（i＝1，2，3）。

根據傅里葉變換，可以得到連續體的熱流通量與溫度梯度之間的關系：

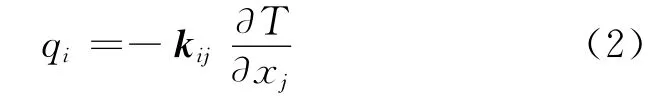
式中：kij為材料在空間方向上的熱傳導率張量，對各向同性材料，熱傳導率在各個方向上保持常數；xj為空間坐標，下標j為方向指標（j＝1，2，3）。

對于離散的體系而言，需要將式（1）進行轉換。假定離散體的總體積為V，單位體積內的熱流通量以qi的散度來表示，在體積為V 的熱存儲器上qi的散度平均值為

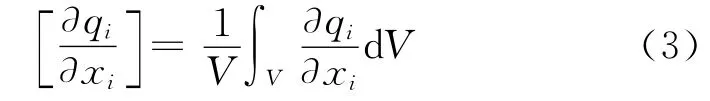
對式（3）通過高斯差分將其轉換為對面積的積分：

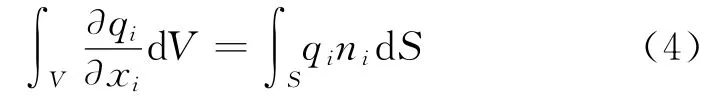
式中：ni為表面向外的單位法向矢量；S 為表面積。

假定離散體中的熱量只在N個熱管中發生流動，從而式（4）可以轉換為

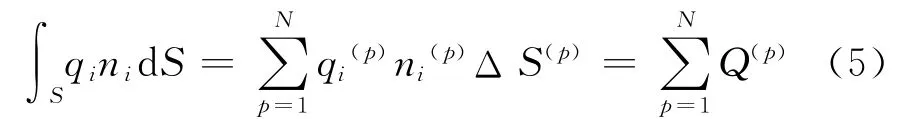
式中：上標（p）為與熱管p相關的變量；Q（p）為從熱存儲器中流經熱管p的功率；ΔS（p）為熱管p的橫截面積。

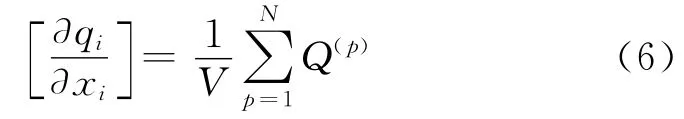
將式（6）代入到式（1）中，可以得到離散體的熱傳導方程：

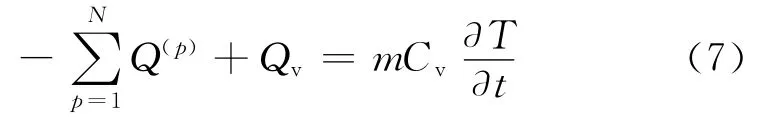
式中：Qv＝V·qv，為離散體的熱源強度；m 為離散體的質量；Cv為連續體材料的比熱容。

如果把單個熱管看作單位長度內具有熱阻η的一維單元，則每個熱管的功率為

式中：ΔT 為熱管兩端的溫度差；l為熱管的長度。

2.2 熱管熱阻與材料熱傳導率的關系

在離散元中，假定單個熱管的熱阻為η，體系中包含N個熱管，總體積為V，則在材料體積V 內的平均熱流通量為

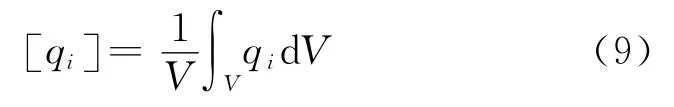
同時，熱量只在熱管內流通，從而上式可以轉換為：

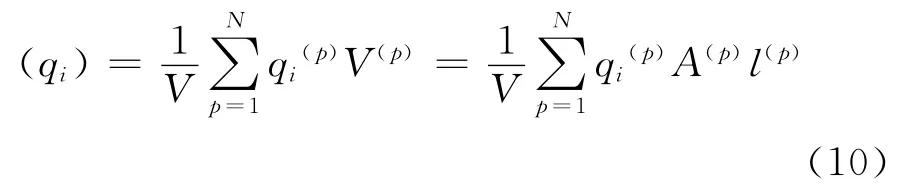
式中：A（p）為 熱 管p 的 有 效 橫 截 面 積；l（p）為 熱 管p的長度。

熱管的熱流通量定義為

將式（8）代入式（11）中，可以得到：

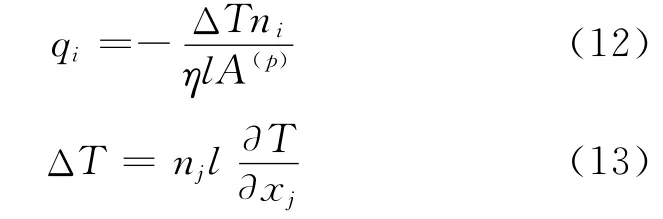
式中：nj為熱管的單位法向矢量；ΔT 為熱管兩端的溫度差。

將式（12）、（13）代入到式（10）中，可以得到：

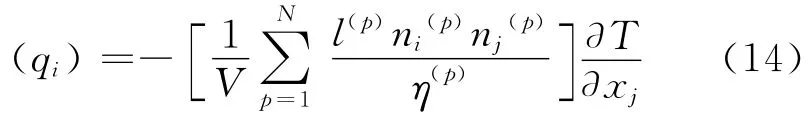
比較式（14）與式（2）可以得到在離散元體系中熱傳導率張量kij：

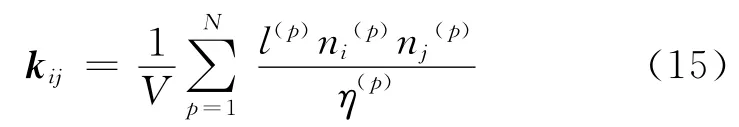
從式（15）可知，只要給定單個熱管的長度、單位法向矢量、熱阻以及總熱管數量等參數就可以計算出離散單元所描述的材料的熱傳導率。

2.3 熱力學耦合計算

在離散元中，材料的熱應變通過顆粒以及顆粒之間連接鍵的熱膨脹來描述，且溫度引起的應變通過改變顆粒的半徑來實現。給定一個溫度的變化ΔT，可以計算出粒子半徑R 的改變量ΔR，即：

式中：α為與每個顆粒相關的線性熱膨脹系數。

如果顆粒之間存在連接鍵（如平行鍵），且熱管是激活的，那么連接鍵的長度ˉL 將在溫度變化時發生相應的改變，從而改變鍵的受力情況。假定在溫度變化時，ˉL 的改變只影響法向力的改變，即：

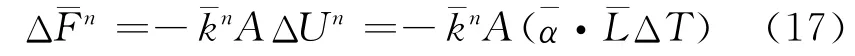
通過以上的推導可知，在離散元體系中材料的熱傳導率通過給定單個顆粒的熱阻來確定，顆粒與顆粒之間的熱傳導以連接鍵的存在為基礎，若產生新的連接鍵或連接鍵發生斷裂，則將改變材料的熱傳導能力。熱量所產生的應變通過改變顆粒的半徑或連接鍵的長度來實現，進而引起材料內部接觸力的改變。

3 碳化硅陶瓷高溫力學性能的模擬與討論

采用前面已校準的碳化硅陶瓷微觀參數，通過施加不同的溫度場以模擬不同溫度下材料力學性能的變化，通過模擬單軸壓縮試驗和三點彎曲試驗來獲得材料的彈性模量、泊松比、抗壓強度及抗彎強度等力學性能參數，模型如圖3所示。單軸壓縮試驗中包含的顆粒數為7 486個，加載速度為0.2 m·s-1；三點彎曲試驗中包含的顆粒數為10 675個，加載速度為0.1m·s-1，顆粒的平均半徑為2μm，最大半徑與最小半徑之比為1.5。為了消除模擬的隨機性所產生的誤差，每個模型分別選取5個不同的隨機數進行模擬，最后取其平均值作為模擬結果。模擬過程中選取9個不同的溫度場（從100 ℃遞增至1 700 ℃，增量為200 ℃）。

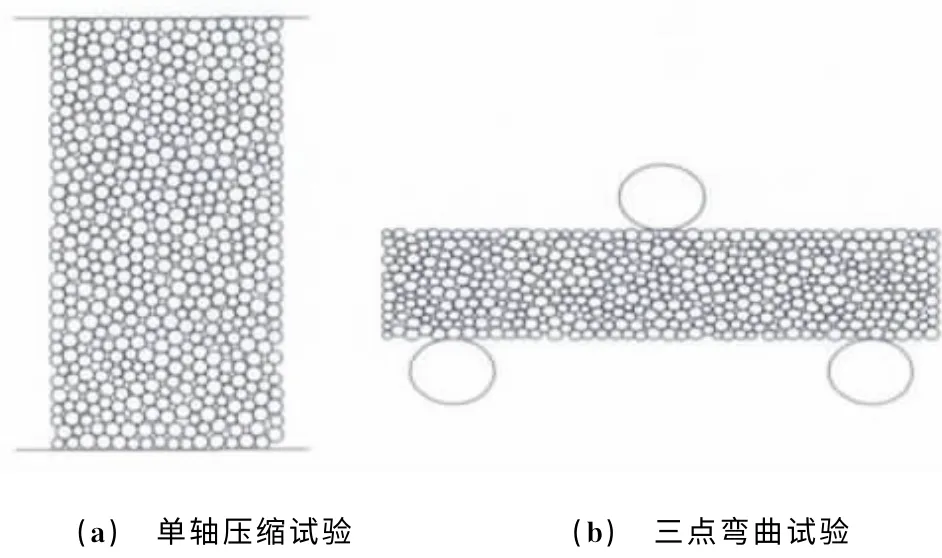
圖3 離散元力學性能測試模型Fig.3 DEM model for uniaxial compression test（a）and three-point bending test（b）

3.1 溫度對力學性能的影響

從圖4中可以看出，當溫度為100～500 ℃時，材料的應力-應變曲線基本一致，這說明在該溫度區間時，溫度對材料的力學性能基本沒有影響。隨著溫度的升高，應力的峰值逐漸降低，對應的應變也相應降低，應力-應變曲線的斜率也逐漸減小，從而表明材料的彈性模量有所降低。對比高溫和低溫區間的失效響應曲線，可以看到材料由最開始的脆性斷裂（500 ℃以下）逐漸向準脆性斷裂（500～1 100 ℃）甚至塑性失效轉變（如1 300 ℃）。應力-應變曲線的結果表明，溫度對材料力學性能有明顯的影響，隨著溫度的升高，材料開始出現一定程度的軟化，其破壞機理也相應發生改變。

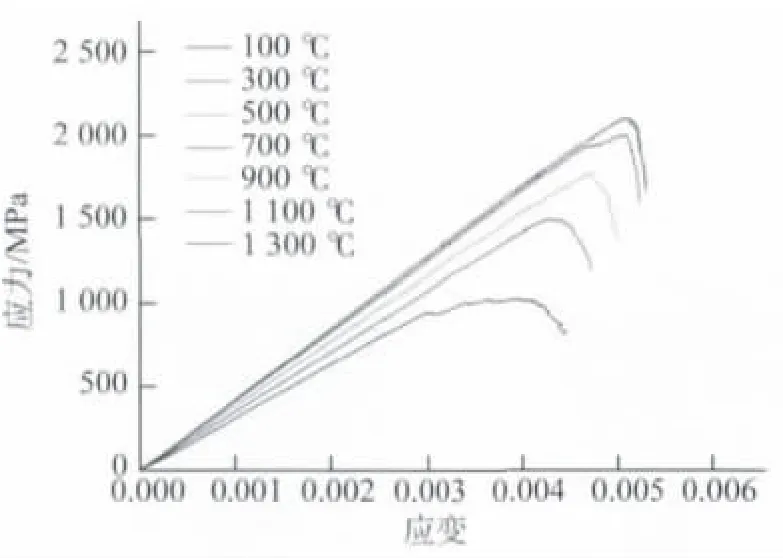
圖4 不同溫度下碳化硅陶瓷單軸壓縮試驗過程中的應力-應變曲線Fig.4 Stress-strain curves of SiC ceramic during uniaxial compression at different temperatures

由圖5（a）可知，隨著溫度的升高，材料的彈性模量逐漸降低，泊松比逐漸增大，這表明材料的抗變形能力降低，在高溫作用下發生了一定的軟化現象。由圖5（b）可見，溫度越高，材料的抗壓強度和抗彎強度越低。力學性能隨溫度的變化曲線同樣表明，在溫度低于500℃時，材料的力學性能變化較小，而溫度一旦持續升高后，其力學性能將發生明顯的改變。

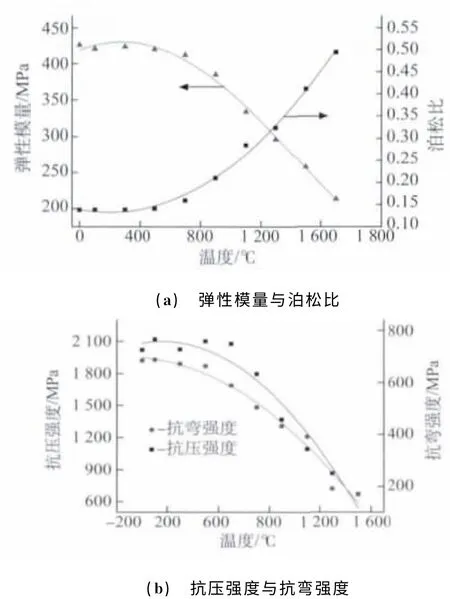
圖5 碳化硅陶瓷力學性能隨溫度變化的模擬結果Fig.5 Simulated results of mechanical properties as a function of temperature for SiC ceramic：（a）elastic modulus and Poisson′s ratio and（b）compressive strength and bending strength

3.2 不同溫度下材料的破壞形態

由圖6可見，當顆粒之間的連接鍵所承受的外載荷大于鍵本身的強度時，連接鍵發生斷裂，此時便認為是新微裂紋產生了。若一系列的微裂紋連接形成曲折的裂紋路徑時，宏觀裂紋便產生了。圖6中的白色線段表示裂紋，可見當溫度較低（低于500 ℃）時，裂紋形成的材料損傷線與底面成45°～50°的夾角，從而表明此時碳化硅陶瓷的破壞形態以脆性斷裂為主；隨著溫度升高（如700，900℃），裂紋的擴展趨勢出現了一定變化，部分裂紋匯合形成的局部宏觀裂紋不再與底面成45°～50°的夾角，但材料的破壞形態依然以脆性斷裂為主；當溫度升至1 100 ℃以上后，裂紋的擴展不再有明顯的規律，且在試樣中間有“墩粗”的跡象，說明此時材料的破壞機理不再是以脆性斷裂為主，而是呈現了一定的塑性變形，且在高溫作用下材料出現“墩粗”現象。

圖6 不同溫度下碳化硅陶瓷單軸壓縮破壞后的形貌Fig.6 Failure morphology of SiC ceramic after uniaxial compression test at different temperatures

4 結 論

（1）建立了脆性材料的離散元熱力學模型，給出了材料微觀熱力學參數與宏觀熱力學參數之間的關系。

（2）建立并校準碳化硅陶瓷材料的離散元模型，模擬了在不同溫度下材料的單軸壓縮試驗及三點彎曲試驗；當溫度小于500℃時，溫度場對材料的力學響應及力學性能參數基本沒有影響，但隨著溫度的逐漸升高，材料的彈性模量逐漸降低，泊松比逐漸增大，抗壓強度和抗彎強度也隨之降低。

（3）結合材料的應力-應變曲線、力學性能參數以及不同溫度下的單軸壓縮破壞形貌可知，隨著溫度的升高，材料的破壞形態由脆性斷裂逐漸向塑性變形轉變，并會使材料出現一定的軟化現象。

［1］OHRING M.Materials science of thin films：deposition and structure［M］.Singapore：Academic Press，2006.

［2］DING Y，NORTHWOOD D O，ALPAS A T.Fabrication by magnetrnn sputtering of Al-Cu-Fe quasicrystalline films for tribological applications［J］.Surface and Coating Technology，1997，96：140-147.

［3］劉孝福，婁延春，蘇貴橋，等.定向凝固用陶瓷型殼高溫力學性能研究現狀［J］.特種鑄造及有色合金，2010，30（10）：913-917，983.

［4］黃小蕭，溫廣武，程顯明.A14SiC4陶瓷的高溫抗氧化性能和高溫力學性能的研究［J］.材料工程，2004（12）：32-35.

［5］白世鴻，喬生儒，舒武炳，等.先進結構陶瓷高溫力學性能測試與表征［J］.材料工程，2000（10）：45-48.

［6］朱偉，肖繼軍，馬秀芳，等.不同溫度下RDX 晶體力學性能的MD模擬［J］.火炸藥學報，2007，30（4）：17-19，24.

［7］王超，梁軍，欒旭.防熱陶瓷材料高溫力學性能及斷裂模式的分子動力學模擬［J］.材料工程，2008（增1）：239-242.

［8］CUNDALL P A，STRACK O D L.A discrete numerical model for granular assembles［J］.Géotechnique，1979，299（1）：47-65.

［9］HUANG H.Discrete element modeling of tool-rock interaction［D］.Minnesota：University of Minnesota，1999.

［10］HZENTZ S，DONZE F V，DAUDEVILLE L.Discrete element modeling of concrete submitted to dynamic loading at high strain rates［J］.Computers and Structures，2004，82：2509-2524.

［11］姜勝強，譚援強，聶時君，等.碳化硅陶瓷預應力加工的離散元模擬 與 實 驗 研 究［J］.無 機 材 料 學 報，2010，25（12）：1286-1290.

［12］TAN Yuan-qiang，YANG Dong-min，SHENG Y .Discrete element method（DEM）modeling of fracture and damage in the machining process of polycrystalline SiC［J］.Journal of the European Ceramic Society，2009，29：1029-1037.

［13］TAN Yuan-qiang，YANG Dong-min，SHENG Y .Study of polycrystalline Al2O3machining cracks using discrete element method［J］.International Journal of Machine Tool ＆ Manufacture，2008，48：975-982.

［14］CUNDALL P A.PFC2D user′s manual［M］.Version 3.Lakewood，Colorado，USA：Itasca Consulting Group Inc，2002.