富鉀鹵水的開發(fā)問題

粟亮 肖風(fēng)凱 甘露 黃藝璇 呂科

(成都理工大學(xué),四川成都 610059)

富鉀鹵水的開發(fā)問題

粟亮 肖風(fēng)凱 甘露 黃藝璇 呂科

(成都理工大學(xué),四川成都 610059)

基于給定數(shù)據(jù)信息,對數(shù)據(jù)的預(yù)處理,并利用Matalb以及Sufer對數(shù)據(jù)進一步操作作出成果圖件解決了對其他鉀含量的推斷,二維,三維鉀含量的分布情況,鉀的高含量區(qū)域劃分以及預(yù)測其它可能的鉀的高含量區(qū)域的問題。

線性方程組 BP神經(jīng)網(wǎng)絡(luò) Sfuer Kriging插值 Matalb

1 背景

早期大量井位中對鉀元素和鈉元素的分析都是測試鉀和鈉的共同含量，而缺乏鉀的單獨含量。因此需要我們建立模型，采用兩種以上的方法推斷各井位的鉀元素含量。其次選擇合理算法，對該儲鹵構(gòu)造的鉀含量的平面分布情況與三維分布情況進行描述。再分別從二維和三維角度建立模型，對該儲鹵構(gòu)造中鉀的高含量區(qū)域進行劃分以及對儲鹵構(gòu)造中其它可能的鉀的高含量區(qū)域進行預(yù)測。

2 符號說明

m1鉀含量，m2鈉含量，m3鈣含量，m4鎂含量，m5鎂含量，m6硫酸根含量，m7重碳酸根鉀含量。

表1 各個井位的K含量

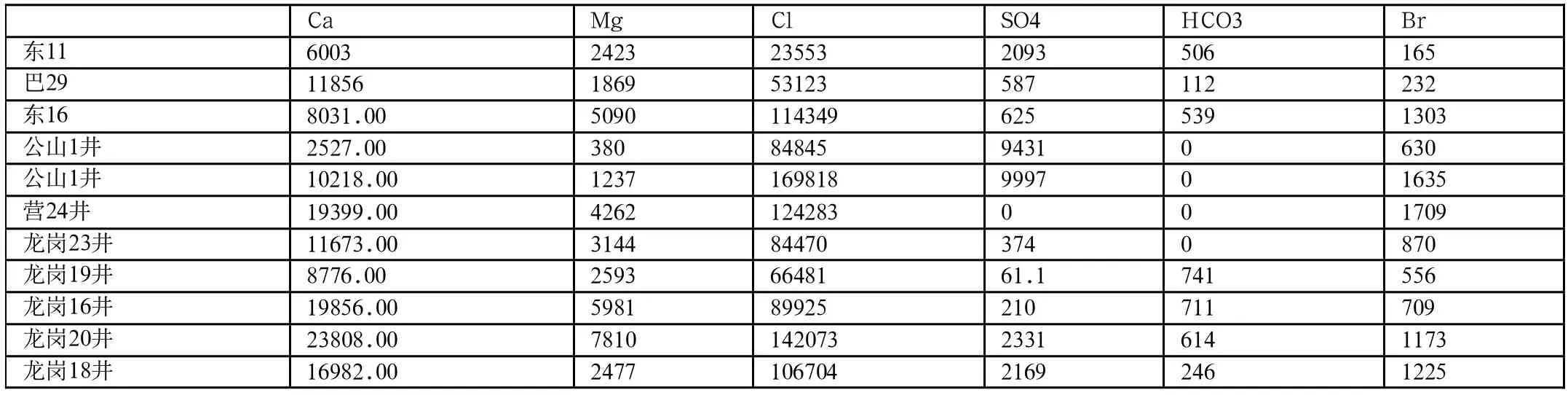
表2 11口井位的數(shù)據(jù)樣本

表3 BP神經(jīng)網(wǎng)絡(luò)的仿真數(shù)據(jù)

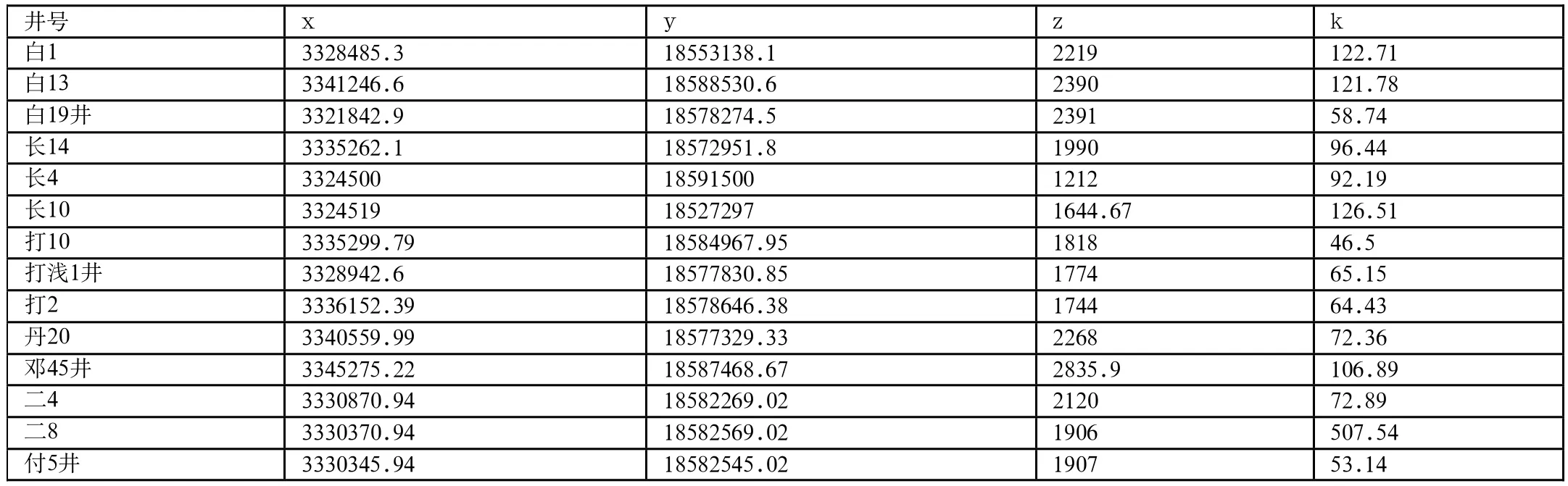
表4 三維原始數(shù)據(jù)

3 模型假設(shè)

(1)在建立基于電荷守恒的方程時，忽略含量較少的陰陽離子的影響(鍶鋇離子、鋰離子、碳酸根、氫氧根以及微量元素)。(2)所給數(shù)據(jù)包括了鹵水中絕大部分的礦物離子。

4 模型的建立與求解

4.1 K含量的推斷

4.1.1 問題分析

根據(jù)表格中已知數(shù)據(jù)求得各井位的鉀元素含量，最基本的方法為建立基于電荷守恒和質(zhì)量守恒的方程組求解之，此外還可以采取多元回歸分析建立K的含量與其他元素含量之間的關(guān)系進行預(yù)測。結(jié)合已經(jīng)給出11口井位的數(shù)據(jù)樣本訓(xùn)練BP神經(jīng)網(wǎng)絡(luò)，來預(yù)測其他井位的K含量，本文采取基于BP神經(jīng)網(wǎng)絡(luò)的預(yù)測方法。

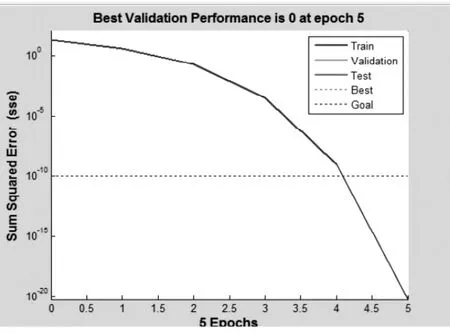
圖1 BP神經(jīng)網(wǎng)絡(luò)逼近精度

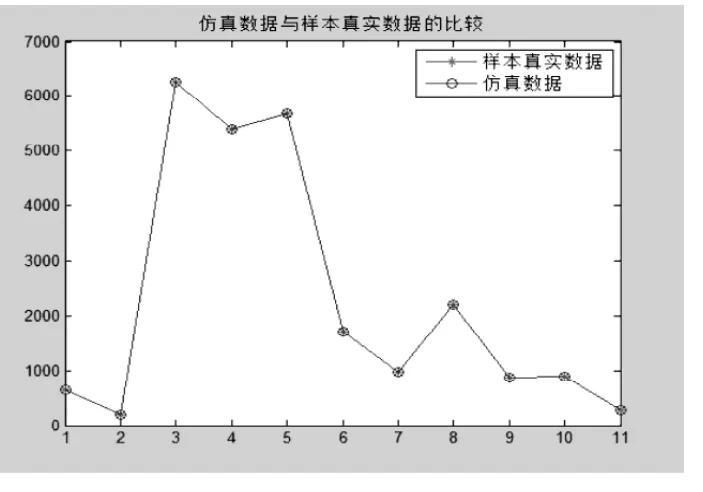
圖2 真實數(shù)據(jù)與仿真數(shù)據(jù)

圖3 z軸的切片

圖4 z軸的切片

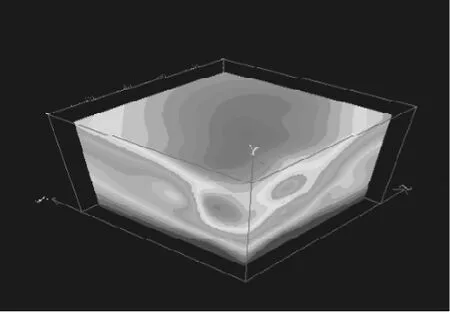
圖5 三維立體圖

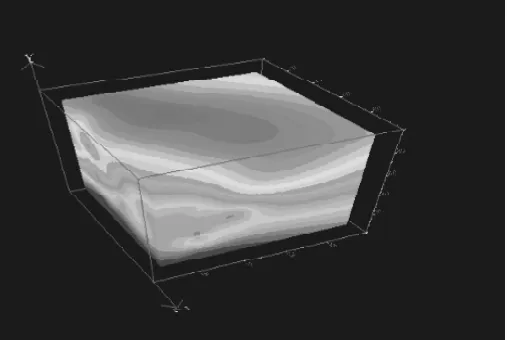
圖6 三維立體圖

4.1.2 方法一 解方程組

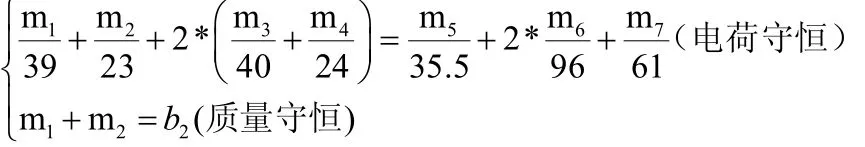
通過matalb編程解以上線性方程組，由此求得的各個井位的K含量為：

4.1.3 基于BP神經(jīng)網(wǎng)絡(luò)的預(yù)測

BP網(wǎng)絡(luò)是1986年由Rumelhart和McCelland為首的科學(xué)家小組提出，是一種按誤差逆?zhèn)鞑ニ惴ㄓ?xùn)練的多層前饋網(wǎng)絡(luò)，是目前應(yīng)用最廣泛的神經(jīng)網(wǎng)絡(luò)模型之一。BP網(wǎng)絡(luò)能學(xué)習(xí)和存貯大量的輸入-輸出模式映射關(guān)系，而無需事前揭示描述這種映射關(guān)系的數(shù)學(xué)方程。它的學(xué)習(xí)規(guī)則是使用最速下降法，通過反向傳播來不斷調(diào)整網(wǎng)絡(luò)的權(quán)值和閾值，使網(wǎng)絡(luò)的誤差平方和最小。BP神經(jīng)網(wǎng)絡(luò)模型拓?fù)浣Y(jié)構(gòu)包括輸入層(input)、隱層(hide layer)和輸出層(output layer)[2]。

4.1.4 基于BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型的建立

我們選取鈣含量、鎂含量、氯根含量、硫酸根含量、重碳酸根含量、溴含量、礦化度七個指標(biāo)作為基本的神經(jīng)元，根據(jù)已知的11口井位的數(shù)據(jù)樣本進行訓(xùn)練，然后利用得到的網(wǎng)絡(luò)來對其他井位的甲含量進行仿真，表2為已知的11口井位的數(shù)據(jù)樣本。

下面為BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練結(jié)果以及樣本真實數(shù)據(jù)與仿真數(shù)據(jù)的比較：

由圖1、2可見該網(wǎng)絡(luò)的收斂性與逼近性極好。

下面是部分BP神經(jīng)網(wǎng)絡(luò)的仿真數(shù)據(jù)。

以上兩種方法中所求得的K含量均存在負(fù)值，考慮到方法一更為精確并且綜合兩種方法，將第一種方法某井位K值為負(fù)值的情況換為BP神經(jīng)網(wǎng)絡(luò)所得的值，得到結(jié)果見附錄2.

4.2 基于Sufer---Kriging法的K含量的二維三維分布模型

4.2.1 克里格法(Kriging)概述[2]

克里格法(Kriging)是地統(tǒng)計學(xué)的主要內(nèi)容之一，從統(tǒng)計意義上說，是從變量相關(guān)性和變異性出發(fā)，在有限區(qū)域內(nèi)對區(qū)域化變量的取值進行無偏、最優(yōu)估計的一種方法；從插值角度講是對空間分布的數(shù)據(jù)求線性最優(yōu)、無偏內(nèi)插估計一種方法。克里格法的適用條件是區(qū)域化變量存在空間相關(guān)性。

克里格法，基本包括普通克里格方法(對點估計的點克里格法和對塊估計的塊段克里格法)、泛克里格法、協(xié)同克里格法、對數(shù)正態(tài)克里格法、指示克里格法、折取克里格法等等。隨著克里格法與其它學(xué)科的滲透，形成了一些邊緣學(xué)科，發(fā)展了一些新的克里金方法。如與分形的結(jié)合，發(fā)展了分形克里金法；與三角函數(shù)的結(jié)合，發(fā)展了三角克里金法；與模糊理論的結(jié)合，發(fā)展了模糊克里金法等等。

應(yīng)用克里格法首先要明確三個重要的概念。一是區(qū)域化變量；二是協(xié)方差函數(shù)，三是變異函數(shù)。

4.2.2 基于Sufer--Kriging插值的模型的求解

4.2.2.1 二維平面模型[3]

求出的數(shù)據(jù)如表4，結(jié)合Sfuer運用Kriging插值將數(shù)據(jù)進行網(wǎng)格化，做出沿著z軸的切片，見圖3、4。

由以上兩圖可見，在等深度的井位的切片上，如果俯視的話，可以看到在二維平面上K含量從右上到左下遞減，其中在中部靠右為K最高含量區(qū)域，此外在頂部還有一處K含量次高區(qū)域。

4.2.2.2 三維立體模型

圖5、6是網(wǎng)格化的數(shù)據(jù)進行體成像后的結(jié)果。

由以上兩圖可見，在三維區(qū)域中有兩個鉀含量較高的區(qū)域；其中一個是在二維平面投影近似橢圓的錐狀體區(qū)域，另外一個是在二維平面投影近似為三角形的柱狀體區(qū)域。

4.2.3 基于二維、三維的鉀的高含量區(qū)域預(yù)測

關(guān)于富鉀區(qū)域的預(yù)測需要結(jié)合巖相古地理標(biāo)志、古水動力場、地質(zhì)構(gòu)造條件等地質(zhì)條件[4]，而本題中所給數(shù)據(jù)不足，我們只能通過Kriging插值后得到三維地質(zhì)體的數(shù)據(jù)進行預(yù)測。在二維平面上，左下方區(qū)域有富鉀的可能性；在三維空間區(qū)域中，則為二維平面區(qū)域向下的延伸。

5 模型評價

采用的兩種推斷鉀含量的方法精度較高，但每種方法中都出現(xiàn)了負(fù)值；采取二維以及三維插值方法--克里金插值解決了空間數(shù)據(jù)連續(xù)性變化的屬性非常不規(guī)則的問題，但是也有自身的缺陷，因此可以嘗試多種插值方法以互相驗證；考慮到數(shù)據(jù)信息的有限性做的純粹基于數(shù)學(xué)的預(yù)測很難保證準(zhǔn)確性，因此有必要獲取跟多信息以更多地結(jié)合地質(zhì)條件進行預(yù)測提高準(zhǔn)確度。

[1]蔣良孝,李超群.基于BP神經(jīng)網(wǎng)絡(luò)的函數(shù)逼近方法及其MATLAB實現(xiàn)[J].微型機與應(yīng)用,2004(1)：52-531.

[2]王仁鐸,胡光道.線性地質(zhì)統(tǒng)計學(xué)[M].北京：地質(zhì)出版社,198814～101.

[3]白世彪,陳曄,王建.等值線繪圖軟件Surfer710中九種插值法介紹[J].物探化探計算技術(shù),2002(5)：157～1621.

[4]林耀庭,曹善行.四川盆地西部發(fā)現(xiàn)罕見的富鉀富硼氣田鹵水[J].中國地質(zhì),2001.28(7)：45-47.