小推力最優軌道轉移問題的UKF估計算法

李 鑒，韓 潮

(北京航空航天大學，北京100191)

0 引言

小推力推進系統具有比沖高、消耗工質少，有效載荷比高，體積小，工作時間長，推力精確可控等特點，所以在空間任務中得到越來越多的應用。

小推力軌道轉移具有機動時間長，非線性強的特點，其優化問題一直是空間軌跡優化領域的研究熱點和難點，目前主要的研究內容是時間最短軌道轉移問題和燃料最優軌道轉移問題。就數值解法而言，連續推力軌跡優化的求解方法可分為直接法和間接法。直接法通過不同的離散化方法對控制量進行參數化，把軌道優化問題轉化為帶有約束的參數優化問題，然后采用非線性規劃算法進行求解。這類方法目前的研究熱點是偽譜法［1－2］，該方法與傳統方法相比具有求解精度較高，尋優參數少，收斂性好的優點，但它仍然需要猜測初值，而且嚴重依賴非線性規劃軟件的求解能力。目前所見文獻中，用偽譜法求解小推力最優軌道轉移問題多局限于同平面圓軌道之間。對于大尺度長時間小推力軌道機動問題，其求解效果尚不明確。

間接法主要通過變分法和極大值原理將原始的連續推力軌跡優化問題轉化為兩點邊值問題，然后利用各種數值方法來求解該問題，常用的方法為打靶法。在應用打靶法求解兩點邊值問題時，有3個難點:(1)需要獲取目標函數或者終值誤差函數對于狀態量和協態變量的梯度矩陣，這些矩陣推導復雜，并且可能出現病態。一般采用數值微分方法避免推導，但精度有限。(2)打靶法對于兩點邊值問題中的協態變量初值很敏感，收斂半徑小，而協態變量又缺乏物理意義，難以估計初值。于是一部分學者研究了協態變量的初值猜測技術，如魯棒性算法［3］，進化算法［4］和粒子群算法［5］。隨機搜索算法雖然可以得到全局最優解，但是計算效率太低，不適合需要長時間積分的小推力軌跡優化問題。Lee［6］提出了一種新的螺旋形軌道協態變量初值猜測方法，但僅適用于平面內軌道機動。(3)控制切換時刻不易確定，文獻［7］提出了控制切換點的搜索算法，但無法保證一定能獲得全部控制切換點。

文獻［8－10］通過構造兩層同倫，以控制連續、求解相對容易的能量最優問題解作為初值，逐步逼近燃料最優問題的解。這樣使每一層優化問題都獲得了良好的協態變量初值，克服了協態變量初值猜測的困難。文獻［11］在文獻［9］算法基礎上對協態變量進行歸一化處理，并加入控制切換點搜索算法和粒子群算法以獲取全局最優解。同倫法具有較高的穩定性、精確性和求解效率，是目前小推力軌跡優化文獻中最有效的算法。但是它引入了兩個新的優化問題，需要另外構造其最優控制律和相關的梯度矩陣，增加了求解的繁瑣程度，并且還需要使用同倫算法程序包，這些都增加了該算法對于工具軟件的依賴程度。

針對上述研究現狀，本文提出一種基于UKF參數估計算法的小推力最優軌道轉移問題求解方法，將軌道機動最優控制問題所對應的兩點邊值問題轉化為參數估計問題，然后用UKF濾波器進行參數估計。該方法流程簡單，不依靠強大的非線性規劃軟件包。其基本原理是估計理論，不依賴梯度信息，故不需要良好的協態變量初值，也不用推導梯度矩陣，同時又具有較好收斂性和精確性，可以很好地解決小推力軌道機動優化問題。

1 小推力軌道最優軌道轉移問題

1. 1 原始優化問題描述

小推力軌道轉移的時間歷程通常很長，飛行圈數可達幾百甚至上千圈，如果采用直角坐標描述航天器的運動會導致狀態量的時間歷程振蕩劇烈，不利于快速積分。本文采用改進春分點軌道要素來描述航天器的軌道運動，這樣既有利于提高積分速度和精度，又避免了可能出現的奇點問題。改進春分點軌道要素［p，ex，ey，hx，hy，L］與經典 Kepler 軌道要素的關系如公式(1)所示:

式中:p為軌道半通徑，a為軌道半長軸，e為偏心率，i為軌道傾角，Ω為升交點赤經，ω為近地點幅角，θ為真近點角。同時，定義如下輔助變量:

以改進春分點軌道要素表示的航天器軌道動力學方程為:

式中:

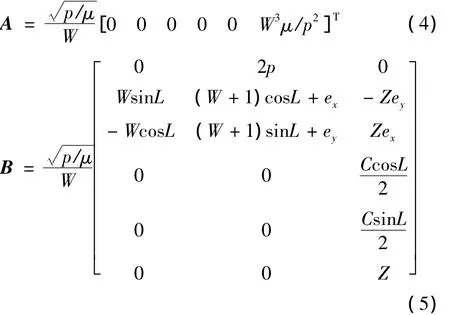
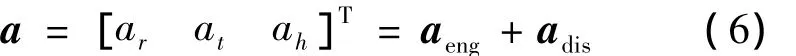
式(6)中，a為除二體引力加速度之外的其他外力加速度矢量，［ar，at，ah］T為 a 在軌道徑向、垂直于徑向和動量矩方向的分量，aeng為發動機推力加速度矢量，adis為其他攝動加速度矢量。本文的討論范圍為只有二體引力加速度和發動機推力加速度情況下的小推力軌道機動優化問題，其他攝動加速度的影響將在后續工作中研究。為簡化起見，在后文公式中用a代替aeng作為發動機推力加速度矢量。

設航天器質量為m，發動機推力大小具有上限Tmax和常值比沖Isp，g0=9.780 4m/s2為赤道重力加速度，則方程(3)～(6)可改寫為

1. 2 最優控制兩點邊值問題

要求解MF問題必須先求解TF問題，因為MF問題的飛行時間必須大于求解TF問題所得的最短飛行時間tfmin。本文基于極大值原理求解最優控制問題，由文獻［9－10］可知，TF問題與MF問題所滿足的狀態變量與協態變量微分方程形式一致，兩種問題的最優控制律也具有相似的形式。應用本文提出的算法求解TF問題與MF問題的過程完全相同，并且TF問題更容易求解，因此將MF問題作為討論重點，對TF問題只給出求解結果以便與文獻的算例作比較。

引入與改進春分點軌道要素對應的協態變量λ= ［λp，λex，λey，λhx，λhy，λL］T和與質量對應的協態變量λm。MF問題的Hamilton函數為:

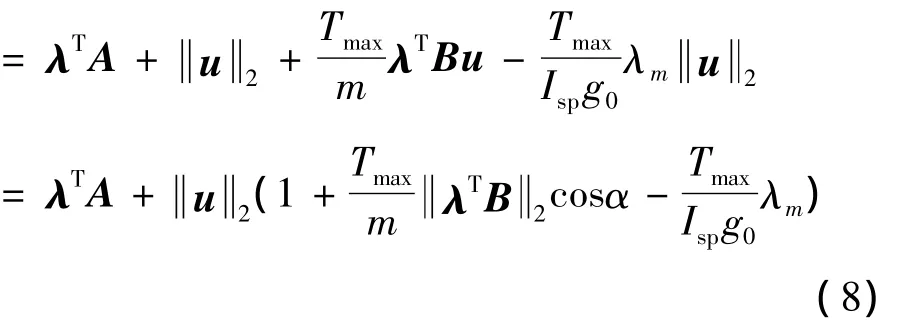
其中α為矢量u與BTu之間的夾角。與終端狀態~x(tf)和終端時刻tf相關的性能指標K為:

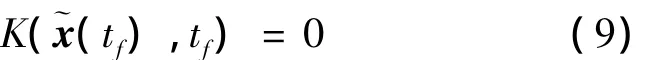
狀態約束為:

系統定常，根據極大值原理，最優控制的必要條件為:

狀態與協態方程:

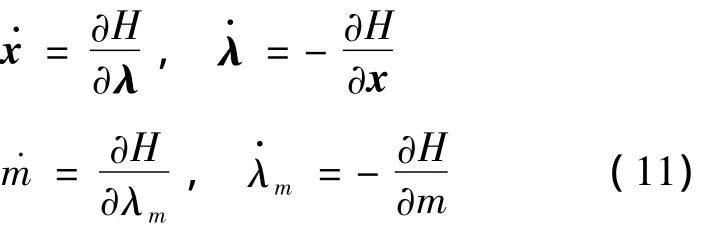
初始條件:

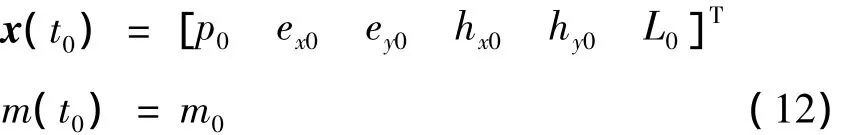
引入狀態約束g的拉格朗日乘子ν，則末值條件為:

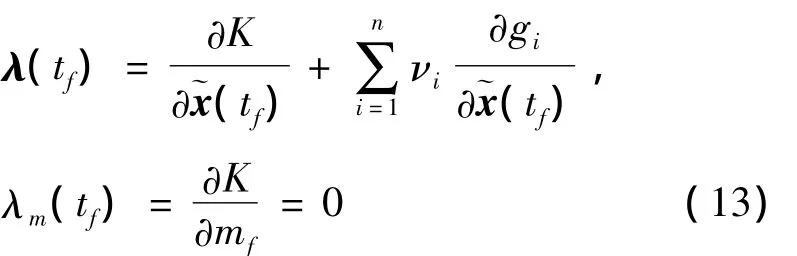
Hamilton函數對最優控制u*有極小值，即:

由式(8)和(14)可知，控制取最優時α=π。系統定常，Hamilton函數不顯含時間，故當控制取最優時H在［t0，tf］上為常數。

考察λm的方程

易知當α=π時，λm的導數非正。又由式(13)可得當控制為最優控制時，tf時刻λm應為0，故λm在［t0，tf］上非負，這一結論對TF問題也成立。令開關函數ψ為:

由文獻［9］可知最優控制律應具有如下形式:

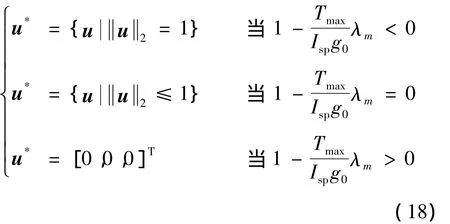
下面討論如何將上述兩點邊值問題改寫成參數估計問題，然后利用UKF濾波估計算法求解。

2 UKF參數估計及其求解方法

參數估計問題，又被稱為系統辨識或者機器學習問題，其目的是為了確定一個非線性映射:

該映射的輸入為xk，輸出為yk，w為非線性映射的參數。一般來說，映射輸入xk和期望輸出dk是不變的，輸出誤差定義為ek=dk－G(xk，w)，求解參數估計問題就是要估計w的均值，使映射G(xk，w)的輸出誤差最小。用濾波器求解參數估計問題的相關理論，文獻［12］作了詳細闡述，本文只作簡要介紹。

將原始參數估計問題寫成狀態空間表達式:

上式代表一個狀態轉移矩陣為單位陣的靜態過程，rk為過程噪聲，而期望輸出dk則與對wk的非線性觀測相對應，ek為觀測噪聲。這樣，原參數估計問題就可以用EKF，UKF等濾波器求解。基于UKF濾波器的參數估計算法流程［12］如圖1所示。

圖1 UKF參數估計算法Fig.1 UKF parameter estimation

UKF參數估計算法公式中，

Rr和Re分別是過程噪聲和觀測噪聲的協方差陣。N是w的維數，η是尺度參數，常量ε決定了UT變換的σ點相對于w當前均值的分布范圍，一般設為小量，取值范圍為［10－4，1］。常量 κ 也是個尺度參數，一般取為0或者3－N。β是與w的先驗分布相關的常量，對于高斯分布，β=2是最優的。ρRLS是遺忘因子，用于防止因模型誤差較大造成的濾波發散，其取值范圍為(0，1］。關于這些常量選取方法的詳細討論可以參看文獻［12］。

參數估計問題相當于求解如下以w為優化變量的優化問題:

式(23)中

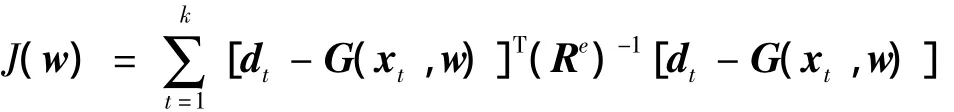
定義觀測誤差為qk=dk－G(xk，wk)，將式(21)重寫為如下觀測誤差形式:

上式表明觀測誤差的期望值為0，求解原始參數估計問題最終轉化為求解式(24)所代表的非線性過程的參數估計問題。

3 UKF參數估計算法求解小推力最優軌道轉移問題

將式(19)代表的燃料最優兩點邊值問題改寫為參數估計問題，選擇待估計參數w為:

觀測誤差為q:

其中G為如下微分方程組初值問題的解:至此，TPBVPMF問題(19)與式(24)形式上一一對應，已轉化為參數估計問題，可通過UKF參數估計算法求解。

4 數值算例與結果分析

首先求解TF問題。以表1給出的初末軌道參數和發動機參數為例，求解不同最大推力值下的時間最短小推力軌道轉移問題，并將計算結果(由PE法表示)與同倫法的計算結果［10］作比較，如表2所示。

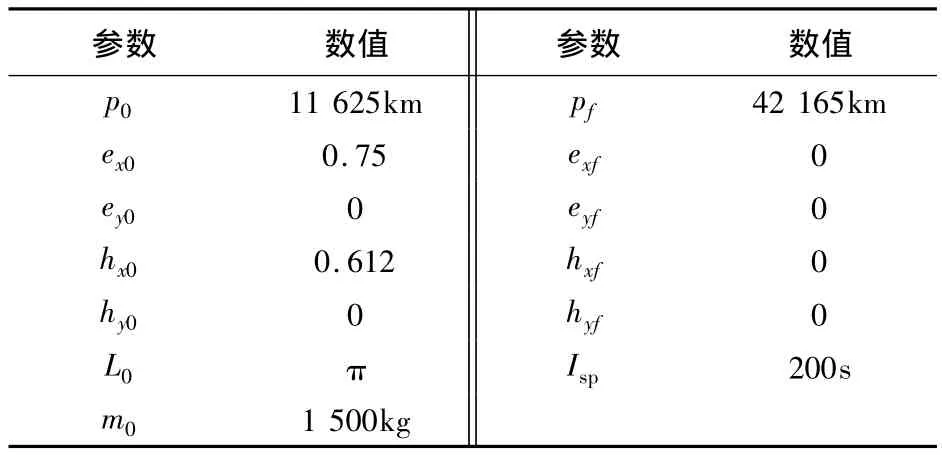
表1 初始計算參數Table 1 Initial parameters

PE法可以直接用隨機初值得到Tmax=0.01N時TF問題的解，文獻［10］只給出了直至Tmax=0.14N時的計算結果，所以在表中沒有數據。

文獻［8］證明了當最大推力值趨近于0時，最小轉移時間和最大推力值之間存在如下簡單關系:

式中C為常數，僅與機動過程的初末軌道參數和發動機參數相關。表2中的PE數據是完全符合上述關系式的，也說明本文算法能夠正確求解時間最短小推力軌道轉移問題。

表2 最短軌道轉移時間Table 2 Minimum transfer times

下面以表1給出的初末軌道參數、發動機參數為例，取飛行時間參數ctf=1.5，求解不同最大推力值下的燃料最優小推力軌道轉移問題，并在表3中與同倫法的計算結果作比較。

文獻［9］所給出的計算條件為SUN-Blade 1 000，本文所得數據的計算條件為Intel i3 3.10GHz，由于沒有確切的計算能力參數，只能根據CPU的浮點計算能力估計后者的計算能力是前者的10倍。由表3可見，兩種方法的求解效率大致相當。

表3 不同T max情況下的燃料最優軌道轉移問題控制切換次數和計算時間Table 3 Switches and computation times of fuel-minimum orbit transfer problem with various T max

可以看出在推力較大的情況下兩者的計算結果是非常吻合的。當推力小于1N時，結果出現了差別，但由表中數據算出的比值仍然是吻合得比較好的，基本上保證了一圈內有2次控制切換，這與文獻［9］中得出的結論一致。數據的差別可以解釋為兩種方法得到了不同的局部最優解。文獻［9］明確指出，求解小推力TPBVPMF問題(19)時極易陷入局部最優解，其具體表現就是相同的飛行時間對應不同的Lf，即不同的飛行圈數。事實上，文獻［9］得到的最優解最終剩余質量大約為1 382kg，而本文算法得到的最終剩余質量約為1 378kg，從實際應用角度出發，這個偏差是可以接受的。

為了驗證本文方法所得結果的精確性，下面以Tmax=10N為例求解TPBVPMF問題(19)，結果如圖2～圖3所示。對比圖2～圖3和文獻［9］的圖示結果，兩者幾乎是完全一致的。圖3中Hamilton函數值在整個機動過程中近似保持不變則驗證了所得結果的最優性。

5 問題與經驗總結

圖2 燃料最優軌道機動問題最優解的軌道要素隨時間變化歷程(最大推力值為10N)Fig.2 Modified equinoctial elements vs time for minimum-fuel orbit transfer problem(T max=10N)

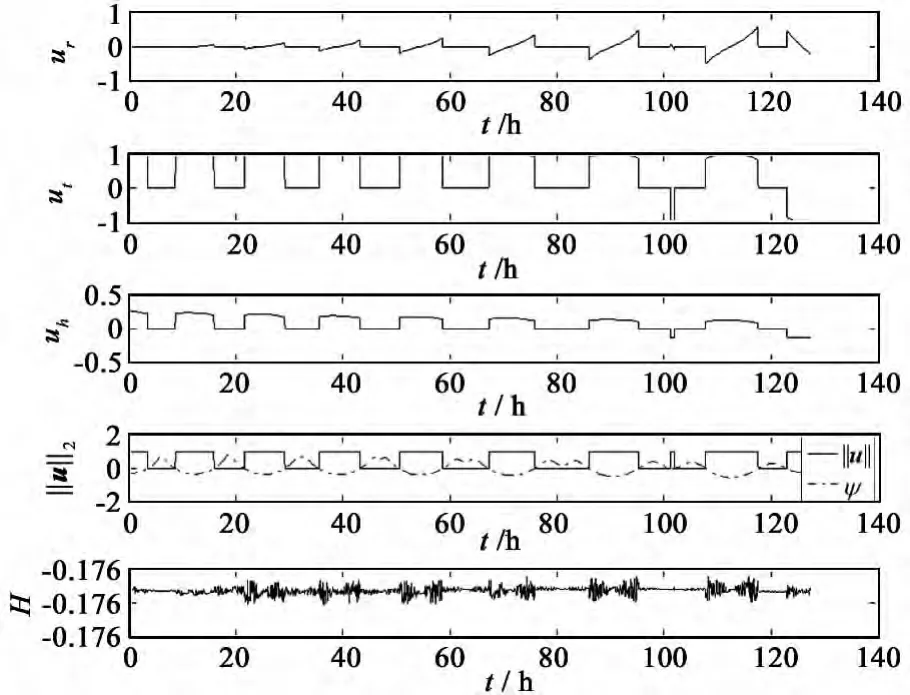
圖3 燃料最優軌道機動問題的最優控制量和Hamilton函數隨時間變化歷程(最大推力值為10N)Fig.3 Optimal control and Hamilton function vs time for minimum-fuel orbit transfer problem(T max=10N)

(1)應用UKF參數估計方法，協態變量初值可以隨機選取，但λm的初值一定要為正。初值的選取范圍與構造問題時使用的量綱是緊密相關的。本文所有算例的長度量綱為106m，時間量綱為小時，以便與文獻［9］對比結果，不一定是最優的選擇。針對不同的軌道轉移問題，選取合適的量綱，使各個協態變量量級盡量接近，可以提高求解效率。

(2)UKF濾波算法公式中的過程噪聲Rr、常量ε和遺忘因子ρRLS對濾波收斂過程的影響很大。這些量的選取和更新方法屬于UKF濾波器算法改進范疇，不是本文的討論重點，可以作為下一步工作。本文通過大量數值仿真，總結常量ε和遺忘因子ρRLS的選取和更新方法如下:對于常量ε，濾波初始階段ε應盡量取較大值(如0.8)，隨著濾波迭代的進行，ε應該隨觀測誤差的減小而減小，這樣有利于算法的快速收斂。本文的算例中，ε最終可減小至0.001。對于遺忘因子ρRLS，當遺忘因子ρRLS較小時，濾波過程的振蕩幅度很大，反之則振蕩幅度較小。推力較大時(1N/1 500kg左右)，采用較小的 ρRLS(如 0.2 ～0.3)，濾波可以很快收斂。當推力較小時，則應采用較大的 ρRLS(如0.5 ～ 0.7)。

6 結論

本文提出的基于UKF參數估計算法的小推力軌道轉移優化設計方法具有簡潔、精確、高效的優點，可作為求解小推力軌道機動優化問題的一個有力工具。

［1］ Ross I M，Gong Q，Sekhavat P.Low-thrust，high-accuracy trajectory optimization［J］.Journal of Guidance and Control，2007，30(4):921－933.

［2］ 尚海濱，崔平遠，徐瑞，等.基于高斯偽光譜的星際小推力轉移軌道快速優化［J］.宇航學報，2010，31(4):1005－1011.［Shang Hai-bin，Cui Ping-yuan，Xu Rui，et al.Fast Optimization of interplanetary low-thrust transfer trajectory based on Gauss pseudospectral algorithm［J］.Journal of Astronautics，2010，31(4):1005 －1011.］

［3］ 劉滔，何兆偉，趙育善.持續推力時間最優軌道機動問題的改進魯棒算法［J］.宇航學報，2008，29(4):1216－1221.［Liu Tao，He Zhao-wei，Zhao Yu-shan.Continuous-thrust orbit maneuver optimization using modified robust algorithm［J］.Journal of Astronautics，2008，29(4):1216 －1221.］

［4］ Igarashi J，Spencer D B.Optimal continous thrust orbit transfer using evolutionary algorithms［J］.Journal of Guidance，Control，and Dynamics，2005，28(3):547 －549.

［5］ Pontani M，Conway B A.Particle swarm optimization applied to space trajectories［J］. Journal of Guidance， Control， and Dynamics，2010，33(5):1429 －1441.

［6］ Lee D H，Bang H C.Efficient initial costates estimation for optimal spiral orbit transfer trajectories design［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1943 －1947.

［7］ Jamison B R，Coverstone V.Analytical study of the primer vector and orbit transfer switching function［J］.Journal of Guidance，Control，and Dynamics，2010，33(1):235 －245.

［8］ Bombrun A，Pomet J B.Asymptotic behavior of time optimal orbital transfer for low thrust 2-body control system［J］.Discrete and Continuous Dynamical Systems，2007(Supplement):122 －129.

［9］ Haberkorn T，Martinon P，Gergaud J.Low-thrust minimum-fuel orbital transfer:a homotopic approach［J］.Journal of Guidance，Control，and Dynamics，2004，27(6):1046 －1060.

［10］ Caillau J，Gergaud J，Noailles J.3D geosynchronous transfer of a satellite:continuation on the thrust［J］.Journal of Optimization theory and Applications，2003，118(3):541 －565.

［11］ Jiang F H，Baoyin H X，Li J F.Practical techniques for lowthrust trajectory optimization with homotopic approach［J］.Journal of Guidance，Control，and Dynamics，2012，35(1):245－258.

［12］ Haykin S.Kalman Filtering and neural networks［M］.USA:John Wiley＆ Sons Inc，2002.