連通率法與Hoek-Brown經驗估算法的力學參數估值比較

叢 璐，宋彥輝，孟祥凌

(1．長安大學地質工程與測繪學院，陜西西安 710054;2．中國水電顧問集團西北勘測設計研究院有限公司，陜西西安 710065)

邊坡巖體的力學參數是影響邊坡穩定性的主要因素，尤其對于發育3組及以上節理的似均質巖體更是如此。目前對邊坡巖體力學參數的選取方法主要包括室內試驗法、原位測試法［1］、連通率法［2］、Hoek-Brown經驗估算法［3］等。室內試驗法只能進行巖塊的試驗并脫離了邊坡的應力環境，因此其結果與邊坡巖體的實際情況相差較大。原位測試法通常采用平洞內的大剪試驗來獲得邊坡的力學參數，該方法被認為是目前確定巖體力學參數最直接的方法，但由于該方法耗時耗資，不便于大量應用，并且試驗尺寸與整個邊坡巖體相比仍顯代表性不足。

連通率法主要是通過建立巖體節理網絡找到巖體中的最大連通路徑，從而了解邊坡潛在的失穩方式，利用巖塊和結構面的力學參數計算巖體的力學參數，從而評價邊坡的穩定性。汪小剛等［4］在確定連通率的過程中考慮了節理和巖橋的組合破壞機制;Zhang等［5-6］分別在二維和隨機不連續三維網絡的基礎上確定連通率;徐光黎等［7］把巖體簡化成一種規則模型來估算其連通率;Einstein等［8-11］通過大量對比試驗對連通率的確定問題進行了研究。

Hoek-Brown經驗估算法是一種常見的估算巖體力學參數的方法，很多學者對這種方法進行了不斷探索與研究，如Cai等［12］為應用Hoek-Brown公式提出了地質強度指數的半定量確定方法;Yang等［13］運用非線性Hoek-Brown準則提出了斜坡巖體等效抗剪強度估算方法，將巖體近似看作均質體，不僅考慮了邊坡不同部位巖體的綜合特征，還特別考慮圍巖應力場環境，估算結果接近于客觀情況，已被大量工程所采用。

本文以鎮安抽水蓄能電站上庫邊坡大理巖的力學參數選取為例，分別運用連通率法和Hoek-Brown經驗估算法對邊坡巖體的力學參數進行估算，以期對比兩種估算結果，分析存在的問題。

1 連通率法

在邊坡穩定性分析中，主要研究邊坡向臨空方向的抗剪切變形能力，即在該方向上邊坡巖體的抗剪強度，為此，首先統計邊坡結構面的發育狀況，獲得各組結構面的優勢產狀及統計規律，如傾向、傾角、跡長、間距等的分布形式及其均值、方差等，以此為基礎進行節理裂隙網絡連通率模擬，并根據完整巖塊及結構面的力學參數計算巖體的力學參數，其中連通率的計算是關鍵。

目前國內常用的連通率法主要有路徑搜索法和帶寬投影法兩種，其中路徑搜索法主要是搜索“最短路徑”(即巖體破壞時需要的剪力最小的路徑)上的連通率來確定巖體的連通率［14］;帶寬投影法則是統計一定帶寬范圍內的、與其破壞方向夾角小于允許值的結構面，然后計算連通率，即

式中:k為巖體連通率;Σ LT為剪切方向上結構面的投影總長度;L為剪切方向巖體的總長度。本文采用帶寬投影法計算巖體的力學參數。

2 Hoek-Brown經驗估算法

通過大量的巖體試驗，并對試驗結果進行統計分析后，Hock和 Brown應用試錯法，于1980年提出了裂隙巖體狹義的Hock-Brown經驗強度準則，并在1992年針對該準則的不足，提出了修正后的經驗公式［15］:

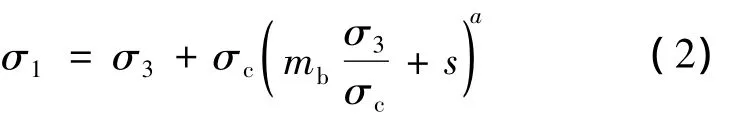
式中:σ1、σ3分別為巖體破壞時的最大、最小主應力;σc為巖塊單軸抗壓強度;mb為經驗參數;s、a為與巖體特征有關的常數。與式(2)相對應的等效巖體力學參數φ與c的計算公式為

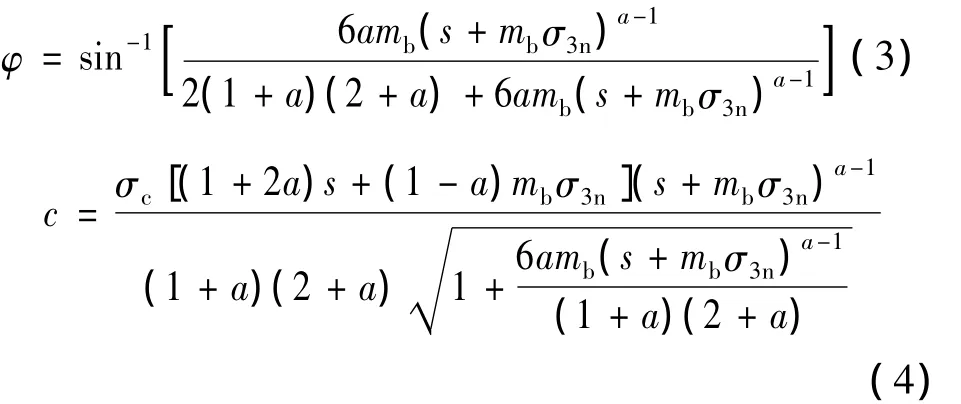
式中:φ為巖體內摩擦角;c為巖體黏聚力;σ3n為側限應力上限值與巖塊單軸抗壓強度的比值。應指出的是，Hoek-Brown經驗公式中的有關參數是通過巖體質量分級體系RMR和地質強度指數獲得的，目前還可應用巖體計算軟件Roclab計算巖體的抗剪強度。

3 實例力學參數估值比較

3．1 工程概況

鎮安抽水蓄能電站位于陜西省商洛市鎮安縣月河鄉境內，地處秦嶺山區，上水庫位于月河右岸支流金盆溝內，水庫正常蓄水位1392.00m，總庫容1172萬m3，死水位 1367.00 m，有效庫容861萬m3，最大壩高120.00 m。

工程區地處秦嶺山區腹地，屬侵蝕山地地貌，上水庫地面高程為1260.00～1330.00 m，左岸最高山峰海拔1729.80 m，右岸黑山海拔2000.90 m。山高坡陡，坡度為 50°～70°，局部為陡崖，岸坡高度約150 m。地表植被繁茂，以生長松木、雜木、灌木等林地為主。區內大小沖溝發育，展布以N-E向為主，少數近S-N向。上水庫岸坡巖性主要為大理巖，其中主要發育 4 組節理:138°∠75°、107°∠74°、80°∠67°、57°∠56°。

3．2 連通率法的力學參數估值

對鎮安抽水蓄能電站上庫右壩肩大理巖進行野外節理統計，得到各組節理的分布特征，如表1所示。

依據表1的節理分布特征進行結構面網絡模擬，在模擬過程中，按照帶寬投影法(帶寬取2 m)計算不同方向的連通率。每次模擬的區域面積為50 m×50 m。為使模擬結果符合結構面分布規律，每個模擬區域均反復模擬多次，由此得到上庫右壩肩巖體結構網絡模擬圖，如圖1所示。

根據圖1的模擬結果，利用自編的結構面模擬軟件求得右壩肩在垂直岸坡方向上的最大連通率為56.13%，可利用經驗公式(5)(6)計算邊坡巖體的力學參數［14］:

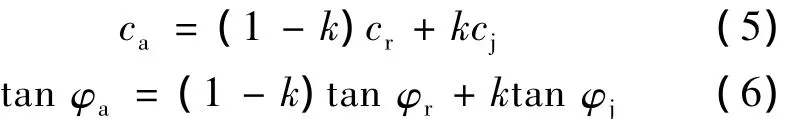
式中:ca、tanφa為節理巖體的綜合抗剪強度指標;cr、tanφr和 cj、tanφj分別為巖橋和結構面的抗剪強度指標。

表1 上庫右壩肩大理巖節理分布特征

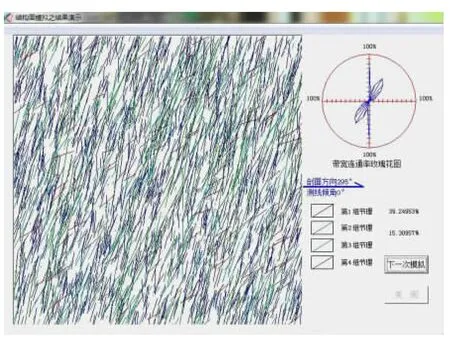
圖1 上庫右壩肩巖體結構網絡模擬

根據室內試驗測得 cr=1.8 MPa，φr=50°;由現場回彈試驗及巴頓公式［16］得到 cj=0.02 MPa，φj=35°;k值取最大連通率56.13%。將數據代入式(5)(6)，求得上庫右壩肩巖體的黏聚力、內摩擦因數分別為0.82 MPa和0.92。

3．3 Hoek-Brown經驗估算法的力學參數估值

首先根據巖體質量分級體系RMR，計算地質強度指數，然后根據式(7)～(9)計算 a、s、mb的值［14］:

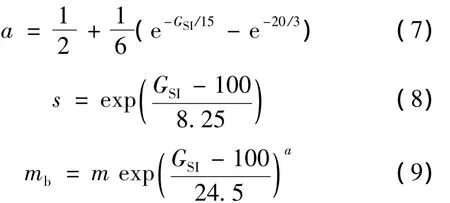
式中:GSI為地質強度指數。σc值根據室內試驗結果測出，σ3n按式(10)計算:

式中:σ3max為側限應力上限值;σcm為巖體的單軸抗壓強度;ρ為巖體密度;H為邊坡高度。利用式(7)～(10)計算出上庫右壩肩大理巖的力學參數為:a=0.505，s=0.0026，mb=1.353，σ3max=2.10，將各參數值代入式(3)(4)，可以得到上庫右壩肩巖體的黏聚力、內摩擦因數分別為0.708 MPa和0.894。

3．4 力學參數估算比較

從前文的估算結果可以看出，連通率法計算的大理巖力學參數與Hoek-Brown經驗估算法的估算值比較接近，后者稍小于前者，其中內聚力約低13%，內摩擦因數約低3%，采用Hoek-Brown經驗估算法時，如果巖體內部發育3組以上節理，可以將巖體近似看作均質體，并不關注某個方向的結構面和巖橋的力學參數，而是考慮巖體整體的力學參數;而采用連通率法計算巖體力學參數時，要考慮最大連通路徑方向上的結構面和巖橋的力學參數。兩種方法的估算結果比較接近，但并不存在確定的大小關系，在實際工程中可根據工程邊坡具體情況并參照有關規范選取較安全的參數。

4 結語

Hoek-Brown經驗估算法已被納入相關工程技術規范，并在國內外諸多工程中得到廣泛運用。本文以鎮安抽水蓄能電站上庫大理巖邊坡工程為實例，分別運用連通率法和Hoek-Brown經驗估算法對邊坡巖體的力學參數進行估算，計算結果表明連通率法的估算結果稍大于Hoek-Brown經驗估算法，但兩者十分接近，因此利用連通率法估算邊坡巖體力學參數也是一種簡便易行的有效方法。

［1］陳祖安，潘家錚，何璟，等．中國水力發電工程:工程地質卷［M］．北京:中國電力出版社，2000:141-145．

［2］肖建勛，程遠帆，王利豐．巖體結構面連通率研究進展及應用［J］．地下空間與工程學報，2006，2(2):325-328．(XIAO Jianxun，CHENG Yuanfan，WANG Lifeng．Development of research of connectivity rate of discontinuities in rock mass and application［J］．Chinese Joumal of Underground Space and Engineering，2006，2(2):325-328．(in Chinese))

［3］CAI M，KAISER P K，UNO H，et al．Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system［J］．International Journal of Rock Mechanics ＆ Mining Sciences，2004，41(1):3-19．

［4］汪小剛，陳祖煜．應用蒙特卡洛法確定節理巖體的連通率和綜合抗剪強度指標［J］．巖石力學與工程學報，1992，11(4):345-355．(WANG Xiaogang，CHEN Zhuyu．Determination of joint persistence and shear strength parameters of rock masses by Monte Carlo method［J］．Chinese Journal of Rock Mechanics and Engineering，1992，11(4):345-355．(in Chinese))

［5］ZHANG X．A two dimensional model of en-echelon jointed rock masses with multi-discontinuity geometry parameters［J］．Rock Mechanics and Rock Engineering，1989，22(3):231-242．

［6］陳劍平，肖樹芳，王清．隨機不連續面三維網絡計算機模擬原理［M］．長春:東北師范大學出版社，1993．

［7］徐光黎，潘別桐，唐輝明．巖體結構模型與應用［M］．武漢:中國地質大學出版社，1993．

［8］EINSTEIN H H，VENEZIANO D，BAECHER G B，et al．The effect of discontinuity persistence on rock slope stability［J］．International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1983，20(5):227-236．

［9］黃建安，王思敬．斷續結構巖體失穩破壞的分離面［J］．水文工程地質，1984，28(3):21-25．(HUANG Jianan，WANG Sijing．Separation plane of instability failure in the fractured structured rock mass［J］．Chinese Journal of Hydrogeology and Engineering Geology，1984，28(3):21-25．(in Chinese))

［10］姚家建，王秋明，馮承樹．緩傾角結構面連通系數的研究［J］．工程地質學報，1989，3(1):43-51．(YAO Jiajian，WANG Qiumin，FEN Chengshu．A study on the connection ratio of lower dip structure plane［J］．Chinese Journal of Engineering Geology，1989，3(1):43-51．(in Chinese))

［11］汪小剛，賈志欣，陳祖煜．巖石結構面網絡模擬原理在節理巖體連通率研究中的應用［J］．水利水電技術，1998，29(10):43-47．(WANG Xiaogang，JIA Zixing，CHEN Zhuyu．An application of discontinuities network modeling principle in the research of discontinuities connection ratio of jointed rock mass［J］．Irrigation Works and PowerTechnique，1998，29(10):43-47．(in Chinese))

［12］CAI M，KAISE P K，UNO H，et al．Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system［J］．International Journal of Rock Mechanics ＆ Mining Sciences，2004，41(1):3-19．

［13］ YANG X L，YIN J H．Slope Equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown Criterion［J］．Rock Mechanics and Rock Engineering，2010，43(4):505-511．

［14］陳祖煜，汪小剛，楊健，等．巖質邊坡穩定分析:原理、方法、程序［M］．北京:中國水利水電出版社，2005．

［15］ HOEK E，WOOD D，SHAH S．A modified Hoek-Brown criterion for jointed rock masses［C］//Proceeding of Rock Characterization，Symposium on International Society of Rock Mechanics．London:British Geotechnical Society．1992:209-213．

［16］劉佑榮，唐輝明．巖體力學［M］．北京:化學工業出版社，2008．