基于ANSYS的起重機新型弧弦主梁力學分析

李新華，陳澤宇，劉 洋

(中南林業科技大學 機電工程學院，長沙 410004)

0 引言

門式起重機是一種搬運大型物料的起重設備，廣泛用于國民經濟的各個部門，在現代化生產中占有重要地位[1]。隨著門式起重機的使用范圍越來越廣，對其安全性能和力學性能也越來越重視。目前市場上的門式起重機中主梁大多采用平直主梁結構，很少采用其他新型主梁結構形式。下承式拱橋隨處可見，因為這種梁-拱組合體系同時具備受彎和承壓的特點而廣泛應用。其結構的主要優點是利用梁的受拉，來抵消拱在豎向載荷下產生的水平推力[2]。本文依據下承式拱橋的受力特點，參照該橋梁的結構形式，提出了一種新型弧弦主梁結構，并利用ANSYS對改進后的主梁進行力學分析。

1 新型弧弦主梁的結構模型

新型弧弦主梁（以下簡稱新型主梁）的結構設計，就是在原來傳統主梁的基礎上，加設一弧形梁，中間通過焊接連桿與平直梁連接，新型主梁結構如圖1所示。

圖1 新型主梁結構

理論上，這種新型主梁可以利用平直梁的受拉來抵消弧在小車豎向載荷作用下產生的水平力，與傳統主梁相比，減小了在豎向載荷的作用下產生的最大應力和應變[3]。圖2分別為傳統主梁和新型主梁的受力簡圖，根據圖2來比較兩種主梁的彎矩及撓度。

1)傳統主梁的彎矩和撓度：

2)新型主梁的彎矩和撓度：

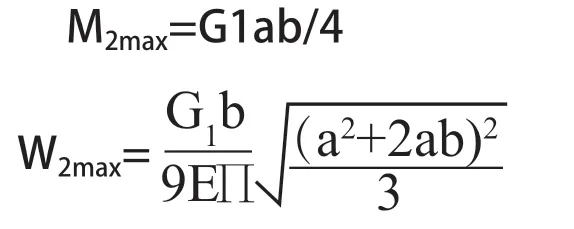
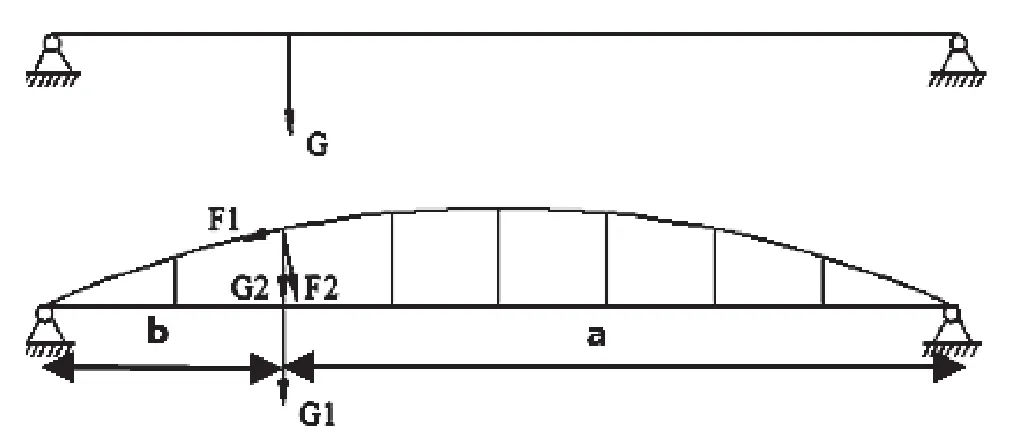
圖2 受力簡圖

由于新型主梁在豎直方向的力被弧梁和拉桿分擔了一部分，則G1=G-G2，其中G為吊重。根據圖1所示，F1=G2Sina；F2=G2Cosa，弧梁和連桿將一部分的豎向力分解成了切向力和徑向力，明顯可得M1max>M2max；W1max>W2max。新型主梁的彎矩和撓度都小于傳統平直梁的彎矩和撓度。理論上證明了在相同的載荷作用下，新型主梁結構上產生的最大應力和應變要小于改進前傳統主梁。

2 有限元建模

2.1 主要參數

該門式起重機的跨度為22.5m，額定起升量Pg=30t，小車的輪距3.6m，兩相鄰大隔板的間距1.5m，隔板厚度0.006m。腹板的高度H=1.3m，兩腹板的間距B=0.5m，腹板的厚度t3=0.006m，上下蓋板的厚度t1=t2=0.016m，主梁的截面圖如圖3所示。

圖3 主梁截面

2.2 模型建立與網格劃分

在ANSYS前處理模塊中分別設置分析類型、單元種類、實常數以及材料參數。在本文中主要采用SHELL63單元和BEAM188單元。SHELL63具有彎曲和薄膜能力，且該平直梁板材的長度不小于其厚度的10倍，應選用SHELL63單元[4]。弧形梁和起連接用作的連桿采用BEAM188單元，該單元適用于應力強化部分，符合弧形梁和接連桿的實際受載情況。建模過程中采用自下而上的方法，通過依次創建關鍵點、線、面等單元達到最終的建模效果。新型梁的材料都采用Q345，其具體參數如表1所示。

表1 材料參數

網格劃分是ANSYS有限元分析的重要環節，網格劃分的方法和類型直接影響單元的規模和分析的計算精度[5]。網格劃分太稀，計算簡便，但是計算精度不高，與實際工作情況相差較大。網格劃分太密，會提高分析結果的計算精度，但同時會使單元規模和計算規模增大，增加計算機的計算負擔，因此要綜合考慮計算規模和計算精度來確定網格大小[6]。本例中，通過多次的計算分析，確定網格大小為0.1m，采用自由劃分產生的節點個數為8494，網格劃分后的有限元模型如圖4所示。

圖4 主梁網格模型

2.3 邊界條件的設置和危險工況選擇

實際情況中，該主梁與端梁是搭接相連的，所以把主梁左右兩端的面上都加上全約束，這樣能比較真實地模擬出主梁與端梁的連接。

根據理論力學和門式起重機工作的實際情況，能夠確定小車滿載制動，置于跨中時，主梁的應變和所受應力值最大，此狀態為門式起重機的最危險工況，應該著重分析。為了使起重機正常、安全地工作，起重機主梁結構應該滿足強度和剛度的要求。對此類門式起重機應按強度計算載荷-第二類載荷，即起重機按工作狀態最大載荷進行強度計算，應選取可能出現對主梁最不利的載荷組合[7]。

2.4 載荷施加

該門式起重機的計算參數：小車自重Pc=8564kg；額定起升重量Pg=30t；動載荷系數φ=1.25；內陸風壓q=150N/m2。工作中，小車運行在軌道上，而軌道鋪在主梁的上蓋板。為了分析簡便，可以認為載荷是直接施加在主梁的上蓋板面上，選擇車輪附近上蓋板面上的節點為受力點，把最大輪壓平均加載在所選的節點上[8]，每個車輪的載荷大小為F=G總/4=120512.5N。

3 靜力學分析

靜力學分析主要是指計算分析結構的應變、應力的分布和大小，用最大的符合應力評價結構的靜強度、最大的符合應變評價其靜剛度[9]。主梁結構主要采用Q345鋼，其屈服極限φ=345MPa，安全系數取n=1.34，主梁的許用應力為 [σ]=σa/1.34=257.5MPa，起重機的許用撓度為[f]=L/800=28mm。

分別對兩種不同起重機主梁在同一危險工況下進行有限元分析，得到的有限元分析結果（如圖5、圖6所示），獲得了起重機主梁在相同工況下改進前后的最大應力和應變的值以及分布情況。

從應力云圖可以直觀看出新型主梁的應力分布比傳統主梁的應力分布更均勻，新型主梁上的弧梁和連桿也相應的承擔了一部分力，在連桿與主梁的連接處、連桿與弧梁的連接處，應力大小為31MPa左右。整個新型主梁結構的應力呈對稱分布，在車輪點處出現應力集中，最大應力為171MPa，這是受到集中力的原因。另外在主梁與端梁的搭接處也出現了應力集中，應力大小為99.4MPa，可能是對主梁結構單獨建模時，僅簡單的在此連接面施加了全約束所致，主梁上其他部分的應力為19MPa。從應變云圖看出，新型主梁的跨中處變形大的范圍減小了，結構的變形也是對稱分布，趨勢是由中間向兩端逐漸變小。

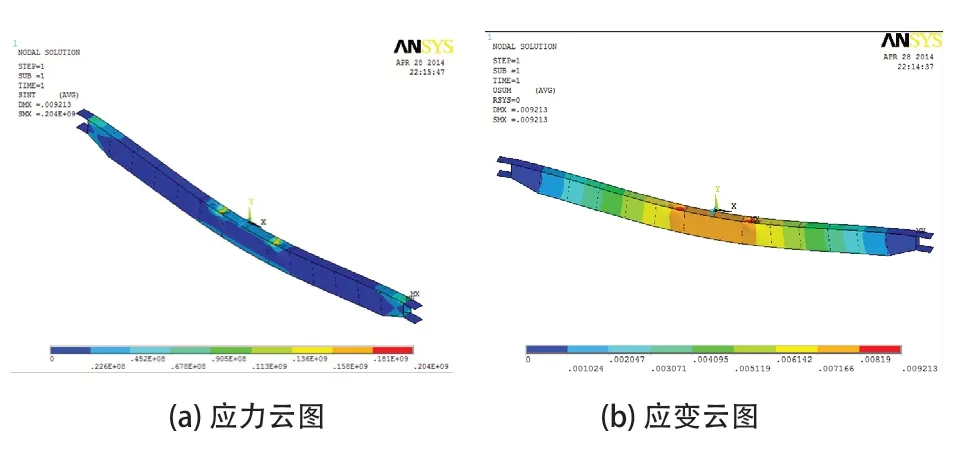
圖5 傳統主梁的應力和應變云圖

從分析結果來看，結構改進前的最大應力是為188MPa、最大應變為9.2mm，改進后的最大應力為171MPa、最大應變為6.6mm，均小于許用的應力和應變，滿足設計的要求。結構改進后的應力、應變的改善量分別為9.04%和26.26%。

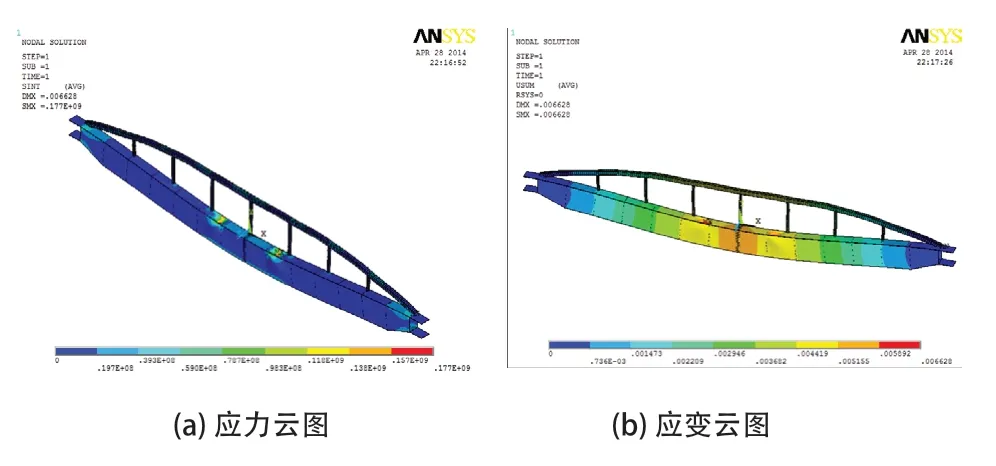
圖6 新型主梁的應力和應變云圖

4 結論

通過對起重機主梁結構改進前后的靜力分析結果的對比，發現新型主梁結構的應力、應變較結構改進之前的應力、應變有所減小。進一步證明了這種新型弧弦主梁結構形式不僅改善了應力、應變的大小和分布狀況，并且有很大的設計余量，在符合設計的前提下，可以對主梁的尺寸優化，達到節約鋼材、降低制造成本的目的，更為起重機的輕量化發展和主梁的新式結構設計提供了參考。

[1]王金諾,于蘭峰.起重運輸機械金屬結構[M].北京：中國鐵道出版社,2002.

[2]姜晨光.橋梁建造技術指南[M].北京：化學工業出版社,2011.

[3]蔣連海,李新華.弧弦梁的研究及其在起重機主梁上的應用[J].制造業自動化,2014,36(7)：76-77,129.

[4]賈振杰,宋曉娟,許映秋,等.基于ANSYS的造船用龍門起重機主梁靜力分析[J].機械制造與自動化,2012,41(5)：98-100,109.

[5]齊玉紅.基于ANSYS的橋式起重機主梁結構優化設計研究[D].鄭州大學,2011.

[6]徐錫鋒,程文明,蔡錕.參照斜拉橋特點的門式起重機結構改進及有限元分析[J].起重運輸機械,2013,(2)：65-68.

[7]戚其松,范小寧,徐格寧,等.基于Ansys的門式起重機主梁優化設計[J].起重運輸機械,2013,(8)：32-35.

[8]秦東晨,齊玉紅.基于ANSYS的30t橋式起重機主梁結構優化設計[J].礦山機械,2011,39(5)：46-49.

[9]姚志林.10t門式起重機結構強度研究[J].建設機械技術與管理,2006,19(7)：96-100.