三次元送料機構干涉曲線設計與研究

黃 偉，楊亞威，李夢群，寧學濤

HUANG Wei1,2,YANG Ya-wei1,LI Meng-qun2,NING Xue-tao1,2

(1.中國科學院寧波材料技術與工程研究所 先進制造技術研究所，寧波 315201；2.中北大學 機械與動力工程學院，太原 030051)

0 引言

在現代化工業領域中，隨著制造業的快速發展，工業自動化程度的不斷提高，用機器取代人工已經成為趨勢[1]。自動送料裝置在很大程度上滿足了企業在生產上的要求。相比人工，自動送料效率高，成本低，安全可靠性強。多工位送料機構已經逐漸替代了傳統的手工送料和單工位送料機構來提高生產效率[2]。然而不同的應用環境要求采用不同的多工位送料機構，這勢必會增加送料機構的設計難度，也使得送料機構的運動軌跡設計更具要求。在進行送料機構設計中，存在一個不可避免的問題即沖壓滑塊與送料機械手在相對運動過程的干涉問題，發生干涉會造成沖壓滑塊與送料機械手發生碰撞，造成機械結構的損壞，所以對送料機構進行無干涉設計以及通過繪制干涉曲線對機構設計和運動軌跡的合理性進行檢查是十分必要的，羅云華等人對行星式送料機構的干涉曲線設計進行了研究，但其方法缺乏通用性，針對這一情況，本文提出一種可應用到多種沖壓送料機構的運動學分析法，并以參數化的形式對可實現聯動的三次元送料機械手進行整個無干涉設計和軌跡規劃。

1 干涉曲線原理

干涉曲線主要是沖壓滑塊在上下沖壓過程中與送料機械手夾持器運動過程中的相對運動關系的圖標和曲線及下模與機械手夾持器的運動關系，是一個三維的空間曲線[3]，如圖1所示。干涉曲線是一種相對運動軌跡，是為了檢驗模具在沖壓過程中與送料機構運動過程中不發生干涉情況的一項指標。在機械結構的設計過程中需要確定的參數包含移送行程、夾取行程、舉升行程、送料桿內寬，每分鐘達到的次數最大搬送重量（制品+夾爪）等[4～6]。以沖壓滑塊的工作位置為基準，畫出送料機械手夾持器的平面干涉曲線圖來直觀的觀察是否發生干涉。通常判斷是否產生干涉的原則是設置其間隙量為30mm，在需要進行干涉檢測的運動過程中其相對運動間隙小于30mm被認定為干涉，否則被認為不干涉。當間隙小于30mm時需要對機械結構或是運動軌跡作出進一步修改，以達到無干涉的要求。

圖1 空間干涉曲線

2 三次元送料周期圖規劃

本文以自主研發設計的三次元送料機械手為研究對象，三次元沖壓送料機械手的主要設計參數如表1所示，送料機械手機構需進行干涉曲線檢查機械運動簡圖如圖2所示。

表1 送料機械手運動參數表

圖2 機械運動示意圖

三次元送料周期是以滑塊的運動周期為基準對機械手夾持器的相對位置以0o～360o的圓周期表示，根據每分鐘沖壓次數為35次的要求，計算出滑塊運動周期約為1.7s。為了保證工件能夠從一工位到下一工位過程中不被沖壓，需要保證沖壓滑塊與送料機械手夾持器在提降、送退、夾張的運動過程中相互配合，協同工作。

本文研發的三次元送料機械手將采用聯動的形式，即提升與送料和松開與回退的過程聯合運動，可提高效率。三次元送料周期可直觀的表示機構工作過程中的提降、移退、夾張的時間分配以及整個運動過程中機械機構運動的軌跡設計發生聯動的時間,整個運動過程中聯動發生在提降與移送以及夾張與回退的過程[7]。根據實際生產的需要可以調控聯動的時間以改善運動軌跡，在設計過程中值得注意的是在夾手夾緊以后和夾手松開以前要停留一段時間以保證工件能夠穩定的放到下模,一般時間為0.02s（轉換成周期的角度變化為50左右。根據沖壓滑塊與送料機械手夾持器在提降、送退、夾張的運動過程中相互配合，協同工作進行時間上的規劃，可繪制如圖3所示的三次元送料周期圖，更直觀的表示沖壓滑塊與送料機械手各個過程的時間分配關系。

3 干涉曲線的參數化無干涉設計與檢查

圖3 三次元送料周期圖

傳統的無干涉設計方法只能針對一種沖壓送料機構進行無干涉設計，本文提出了一種可以滿足不同種類的沖壓送料機構的運動學分析法通過參數化的方式進行無干涉設計及優化。通過B樣條曲線對三次元送料機械手的機械機構進行運動學分析，以參數化方式進行送料機構的軌跡規劃和無干涉設計。

B樣條曲線是一種靈活的曲線，曲線的局部形狀受相應頂點的控制很直觀[8]。通過對頂點控制技術，可以使整個B樣條曲線在某些部位滿足一些特殊的技術要求。B樣條曲線表達式為：

在上式中i=0,1,2,…,m，Pi+k為控制頂點，Fk,n(t)為B樣條基函數，可以看出：B樣條曲線是分段定義的。如果給定m+n+1個頂點Pi(i=0,1,2,…,m+n)，則可定義m+1段n次的參數曲線。

在以上表達式中：Fk,n(t)的n次B樣條基函數，也稱B樣條分段混合函數。其表達式為：

式中k=0,1,2,…,n連接全部曲線段所組成的整條曲線稱為n次B樣條曲線。

依次用線段連接點 Pi+k(k=0,1,…,n)所組成的B樣條曲線在tk時刻每個點是S(tk)表示為：

為了避免三次樣條函數曲線過渡不平滑[9]，本文采用五次B-spline樣條曲線對X-Y-Z三軸的軌跡進行規劃。

根據軌跡規劃每兩段相鄰曲線在連接點處位置、速度、加速度、加加速度連續得出以下關系：

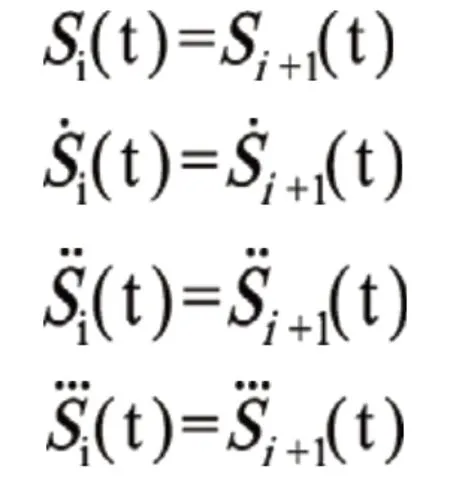
參數化設計是指零件和部件形狀比較定型，用一組參數約束該幾何形狀的一組結構尺寸序列，參數與設計對象的控制尺寸有顯示對應，當賦予不同參數時，就可以驅動原幾何圖形達到新的目標幾何圖形[10]。設計人員根據工程關系和幾何關系來指定設計要求。每次改變這些設計參數時來維護尺寸或工程參數的初值這些基本關系[11]。本文對三次元送料機械手進行運動學分析，運用python軟件進行編程，把運動學方程以語言的方式寫入程序通過更改送料全過程的時間分配或周期運動參數，來調節送料機構與沖壓滑塊周期曲線來進行機構的參數化設計，達到無干涉設計的目的。通過參數化設計可以大大提高模型的生成和修改的速度，在產品的系列設計方面提高了工作效率和工作質量，具有較大的應用價值。

3.1 機械手送退夾張提降周期曲線

根據沖壓滑塊與機械手的相對運動關系和三向周期表可知，當沖壓滑塊開始運動時，移送已經進行了半個移送的行程，把沖壓上死點時刻設為整個周期運動的起始時刻0時刻。根據移送和回退行程以及沖壓的周期為1.7s，分別規劃送退、夾張、升降的運動點，再通過B樣條曲線進行五次插值。X、Y、Z在周期內對應的運動坐標如表2 所示

在滿足沖壓滑塊與機械手送料、夾張、升降在同一時間內協同工作的條件下，采用Python編程軟件，根據五次基樣條曲線進行插值運算，通過反復調節時間參數最后可得到合理的三向送料機械手與沖壓滑塊的運動周期曲線如圖4所示，圖4直觀反映了沖壓滑塊運動一周期與進退、夾張、升降運動曲線的相對關系。

圖4 三向送料周期曲線

3.2 干涉曲線

研究機械手送料過程中的干涉問題主要考慮沖壓滑塊和送料機械手夾持器干涉、下模同夾持器及產品的干涉。沖壓滑塊同夾持器關系表現在解除夾緊、送料、退料的過程。下模同機械手上夾持器干涉主要表現在送料過程。

3.2.1 下模與送料機械手夾持器的干涉檢查

下模固定于整個機械支架上面，下模的位置不隨整體機構的運動而改變，下模與夾持器的設計關系如圖5所示，從圖5可看出我們只需檢查要機械手夾持器在運動過程中是否會對下模產生干涉即可（夾持器與下模間隙不下于25mm）。

表2 沖壓周期時間t與規劃點對應關系

圖5 下模與夾持器的關系

通過B樣條曲線以下模為基準對機械手夾持器進行軌跡規劃，機械手夾持器升降與移送過程和夾張與回退的過程部分編寫程序，得出送料過程中與下模的干涉以及送料退料過程上下平面的干涉曲線，如圖6所示。

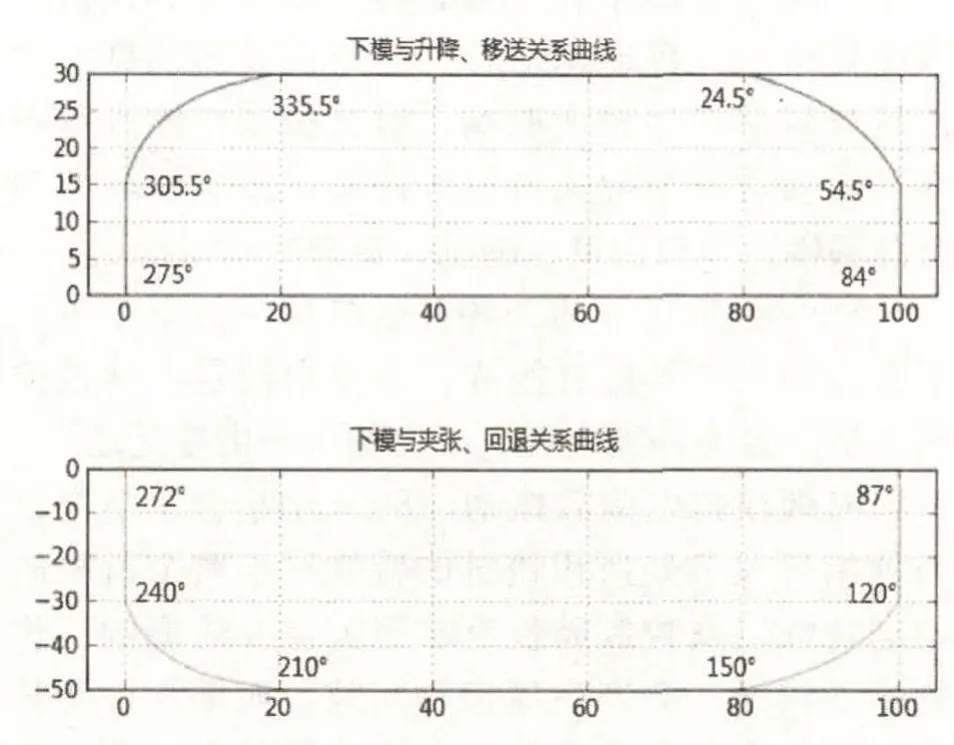
圖6 下模與機械手的干涉曲線

3.2.2 沖壓滑塊與送料機械手的干涉關系

沖壓滑塊與機械手夾持器一直處于空間運動關系，沖壓滑塊以行程為100mm，以周期為1.7s進行周期運動的沖壓運動，為了使干涉檢查更直觀，將采用相對位置曲線表示沖壓滑塊與送料機械手的關系。沖壓滑塊每進行一周期要轉動3600，以沖壓滑塊曲柄轉動的角度變化為基準，反映機械手夾持器的運動軌跡，從而使得從時間和空間上更直觀的表示沖壓滑塊與進給、回退、夾張的干涉問題。圖7是從運動分析的角度，繪制空間干涉曲線，對沖壓滑塊和機械手夾持器進行干涉曲線的繪制和無干涉設計。

圖7 沖壓滑塊與夾持器干涉曲線

4 結論

本文總結以往干涉設計的不足提出了一種可對多種沖壓送料機構進行干涉曲線設計和檢查的方法——運動學分析對機構的干涉曲線進行參數化設計，得到三次送料的周期曲線、下模與機械手夾持器的干涉曲線以及沖壓滑塊與機械手夾持器的整個運動過程的空間干涉曲線，以運動學參數化的方式能夠更直觀更快速的檢查機械結構以及軌跡的規劃是否合理性并能夠迅速改正，為機構設計提供更有價值的參考。

[1]南雷英,戚春曉,孫友松.沖壓生產自動送料技術的現狀與發展概況[J].鍛壓裝備與制造技術,2006,41(02):18-21.

[2]方芳,李承璋,方孝安.模具自動化改造技術[J].汽車工藝與材料,2011,31(06):51-57

[3]李傲宏,朱雷.干涉曲線在多工位模具生產線中的應用[J].模具制造,2010,10(03):77-79.

[4]羅云華,張祥林,張穎,黃早文.多工位自動送料系統的無干涉設計與研究[J].鍛壓技術,2004,29(05):49-52.

[5]謝丹.汽車左右前地板多工位級進模設計方法[J].模具制造,2011,11(05):27-29.

[6]成虹,主編.沖壓工藝與模具設計[M].北京市:高等教育出版社,2006.

[7]華中工學院等五院（校）《機械傳動及曲柄壓力機》編寫組[M].機械傳動及曲柄壓力機.北京市:人民教育出版社,1976.

[8]S.A.Bazaz and B.Tondu.Minimum time on-line joint trajectory generatorbased on low order spline method for industrial manipulators[J].Robotics andAutonomous Systems,29(04):257–268,1999.

[9]L.Biagiotti and C.Melchiorri.Smooth trajectories for high-performance multi-axes automatic machines[A].In Proc.4th IFAC Syposium on Mechatronic Sys-tems[C].Heidelberg,G,Sept.1(02):175-180,2006

[10]陳帆,馬志良.基于設計邏輯的參數化模型建立及其特點[J].建筑與文化,2014,15(01):126-127.

[11]孟祥旭,徐延寧.參數化設計研究[J].計算機輔助設計與圖形學學報,2002,14(11):1086-1090.