基于ADINA的鉛芯橡膠支座對渡槽隔震效果的數值模擬

王化翠，盧興旺，苑司樂

（1.河海大學水利水電學院，江蘇南京210098；2.天津市濱海水業集團股份有限公司，天津300381；3.河南黃河勘測設計研究院北京分院，北京100073）

渡槽的地震安全問題一直都是水工結構抗震領域內關注的焦點之一，由于該類結構上部水體產生的巨大質量及薄壁槽身，使其結構具有不同于一般結構的特殊性，在理論研究、試驗研究、設計經驗方面缺乏相對成熟的依據［1］。由于渡槽和橋梁在結構形式上十分相似，因此借鑒成熟的橋梁結構減震、隔震研究成果是解決問題的有效途徑。傳統的工程結構抗震思想是依靠增加結構的剛度，然而對地震作用的抑制并不是十分顯著，而且不利于優化結構體型，節約資源。近些年來，隔震技術在實際工程中得到了廣泛的應用。在已發生的幾次大規模地震中，采用隔震技術的建筑物都達到了預期的目標，體現了良好的抗震性能［2］。鉛芯橡膠支座是目前應用比較廣泛的一種隔震支座［3］，大量實際地震驗證了它具有良好隔震效果。鑒此，本文基于有限元程序ADINA建立鉛芯橡膠支座以及渡槽隔震結構的數值分析模型，研究鉛芯橡膠支座的非線性滯回特性及其對渡槽結構的隔振效果，以期為結構抗震設計提供科學合理的參考依據。

1 研究理論與方法

1.1 鉛芯橡膠支座的雙線性分析模型

橡膠材料具有超彈性，在荷載作用下發生大變形大位移，表現出強烈的非線性特征。在ADINA程序中有多種材料模型用來模擬橡膠，本文選擇常用的Mooney-Rivilin模型研究分析橡膠材料的特性。橡膠材料的應力-應變關系是由應變能密度函數W定義的，對于Mooney-Rivilin模型而言應變能密度函數W是應變不變量I1和I2的函數［4］，即

式中：C1和C2是材料力學性能常數。

鉛是一種理想的彈塑性材料，應力-應變曲線在屈服前呈彈性關系，屈服后塑性段曲線斜率為零，選擇ADINA程序中的Bilinear模型來模擬鉛的材料特性。鉛的屈服應力較低，在塑性變形條件下還具有較好的疲勞特性，是一種較好的阻尼器，鉛芯橡膠支座具有良好的滯回特性，滯回曲線飽滿而穩定，滯回曲線近似呈現為雙線性行為。日本、新西蘭規范均建議采用雙線型模型，我國的抗震分析中一般也采用雙線型模型進行分析計算［5］。圖1為鉛芯橡膠支座的雙線性模型，圖中Qy為鉛芯的屈服力，K2為屈服后剛度，K1為屈服前剛度。

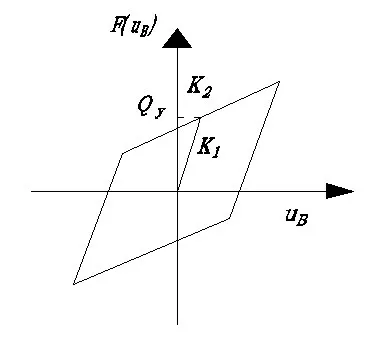
圖1 鉛芯橡膠支座的雙線性模型Fig.1 The bilinear model of lead rubber bearing

1.2 動力分析方法

結構體系的動力平衡方程表示為［6］

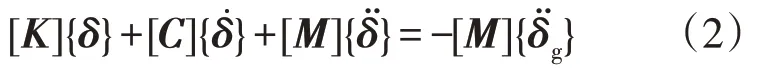
式中：{δ}，，分別為結構的節點位移、速度和加速度列陣；為地震時地面運動加速度列陣；[K]為系統的整體剛度矩陣；[C]為系統的整體阻尼矩陣；[M]為結構的集中質量矩陣。

時程分析法可以觀察到結構在不同時刻下結構的動力響應，并且可以計算非線性動力問題。考慮到鉛芯橡膠支座的非線性力學特性，本文在分析地震作用時采用時程分析法。

1.3 ADINA流固耦合理論

渡槽中的水體采用ADINA勢流體單元模擬，基于亞音速速度公式的勢流體流固耦合有限元方程為［7］：

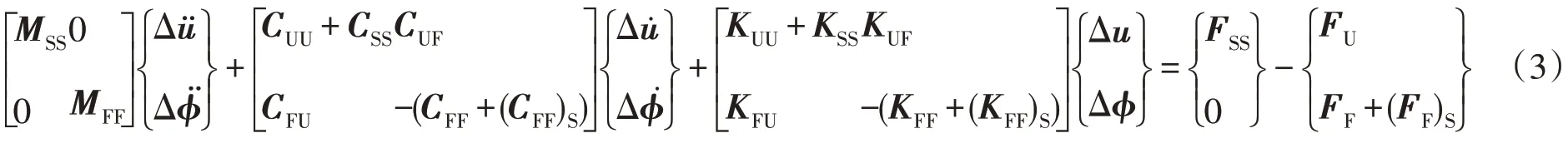
式中：Δu，Δφ分別為未知的位移矢量增量、勢增量；MSS，CSS，KSS，FSS分別為結構的質量、阻尼、剛度矩陣和荷載矢量；MFF為流體質量矩陣；CUU，CFU，CUF，CFF分別為流固耦合界面上固體自身的、固體對流體造成的、流體對固體造成的、流體自身的阻尼矩陣；KUU，KFU，KUF，KFF分別為流固耦合界面上固體自身的、固體對流體造成的、流體對固體造成的、流體自身的剛度矩陣；FU，FF，()S分別為結構邊界所受的流體壓力、流體連續性方程對應的體積分與面積分。

2 鉛芯橡膠支座數值模型的算例驗證

2.1 鉛芯橡膠支座有限元模型的建立

本文選用文獻［4］中的鉛芯橡膠支座作為有限元計算的原型，通過有限元計算與試驗結果的對比驗證本文有限元計算的正確性。鉛芯橡膠支座的尺寸是300 mm×300 mm，一共有10層橡膠，每層3.5 mm；9層鋼板，每層2.2 mm；上下封板20 mm；中間鉛芯直徑70 mm。

鉛芯在灌入橡膠板和鋼板孔時，鉛芯的體積比孔的體積大，鉛芯被牢固的壓入孔中，橡膠支座發生水平位移的時候，鉛芯是被迫發生剪切變形的，因此鉛芯可以與橡膠板和鋼板共節點；在鉛芯橡膠支座的實際工作狀態中，極少出現橡膠板與薄鋼板的剝離現象，兩者是在高溫高壓下粘結形成的，可將橡膠板與薄鋼板共節點。在ADINA中使用3D solid單元建立鉛芯橡膠支座有限元模型，如圖2所示，整個有限元模型一共有15 729個節點，15 360個單元。約束條件為底面固定約束，四周自由。計算方法采用1節介紹的理論與方法進行計算分析。

2.2 有限元分析結果與試驗結果的對比

本文僅對文獻［4］中的工況一進行模擬，工況一是在0.05 s內施加12 MPa 的均布豎向荷載，保持豎向荷載不變，以0.2 Hz頻率施加支座剪切變形γ=100%的水平正弦曲線位移荷載。圖3是有限元結果和試驗結果的對比圖，驗證了本文有限元分析程序ADINA數值模擬方法的正確性。

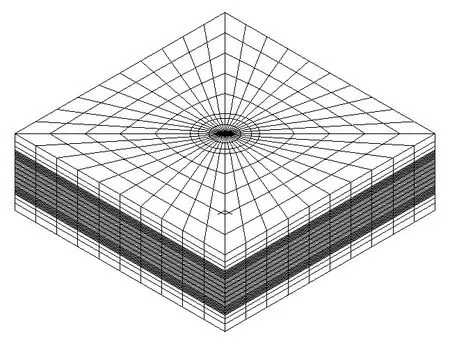
圖2 支座的有限元模型Fig.2 3D finite element modal

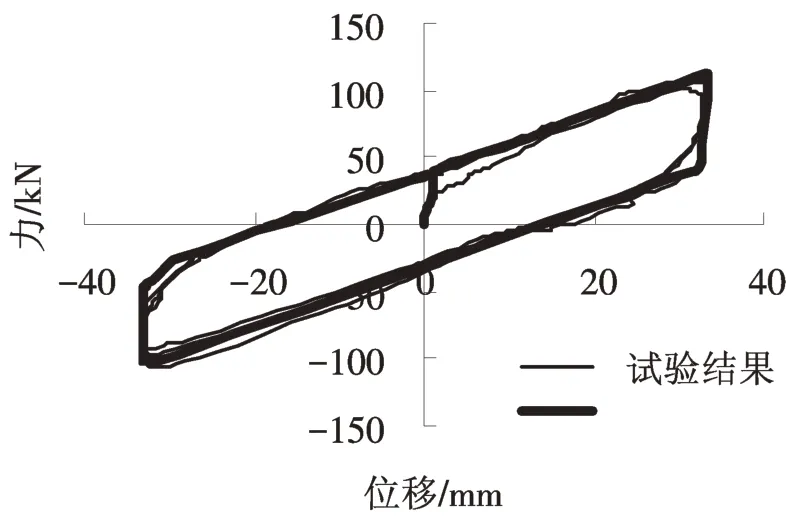
圖3 有限元結果與試驗結果對比Fig.3 The comparison of the finite element and test results

3 實際工程應用

3.1 工程概況與有限元模型的建立

某渡槽實際工程單跨23 m，槽體底寬6 m，槽體高4.5 m；槽內水體寬5 m，高2.7 m；下部支承結構型式為實體重力墩，由墩帽、墩身、承臺組成，槽體與墩臺之間共設置4個鉛芯橡膠支座，槽身為鋼筋混凝土結構。槽體混凝土C50，墩帽混凝土C40，墩體和承臺混凝土C25，工程為Ⅱ類場地，設計地震烈度為7度，地震動峰值加速度為0.1 g。為研究隔震支座在地震作用下對渡槽結構的隔振效果，分別建立了該渡槽的有限元隔震模型和非隔震模型。槽體、槽墩、承臺采用3D solid單元模擬；水體采用勢流體單元模擬，運用ADINA流固耦合算法考慮動水壓力；鉛芯橡膠支座采用非線性彈簧單元模擬。坐標軸規定：X向為順槽向，Y為橫槽向，Z為豎向。混凝土材料參數：C50彈性模量取33.5 GPa，泊松比取0.167，密度取2 500 kg·m-3，C40 彈性模量取32.5 GPa，泊松比取0.167，密度取2 500 kg·m-3，C25彈性模量取28 GPa，泊松比取0.167，密度取2 500 kg·m-3，混凝土動態彈模參數較靜態彈模參數提高30%。鉛芯橡膠支座的屈服前剛度為8.26×106N·m-1，屈服后剛度為2.36×106N·m-1，屈服力為159 kN。圖4為本文建立的有限元分析模型。

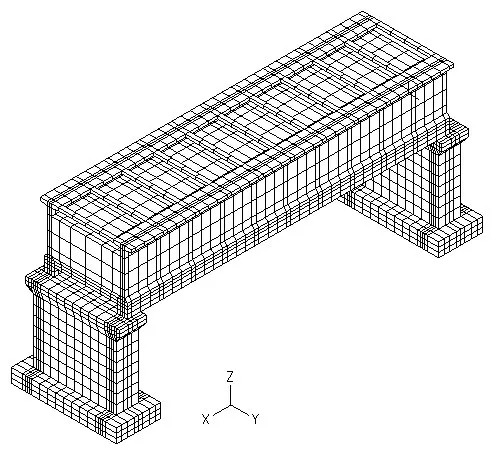
圖4 渡槽有限元模型Fig.4 3D finite element modal of aqueduct

3.2 結構自振特性分析

分別對隔震渡槽結構和非隔震渡槽結構進行結構自振特性分析，提取結構的前6階模態進行分析，兩種模型的頻率見表1，由表中數據可知，渡槽使用隔震支座時每階頻率均有不同程度的下降，第一階頻率降低了47%，這充分說明隔震支座對降低頻率、延長結構周期起到明顯的效果。具體延長的多少與結構自身的特性、隔震支座的特性有關，可以通過改變支座力學參數來適當調整結構的周期。從振型方面看，隔震和非隔震結構的振型大體相同，僅在第7階振型之后發生了變化。

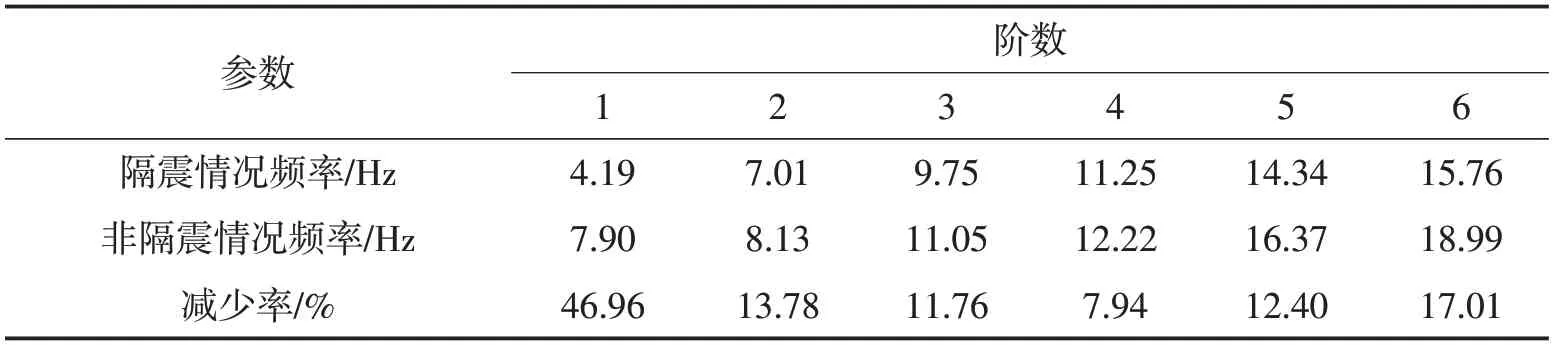
表1 隔震與非隔震兩種情況下的頻率對比表Tab.1 The frequency comparison in isolated and non-isolated conditions

3.3 地震反應分析

為了研究設置鉛芯橡膠支座后渡槽抗震性能，本文運用時程分析法對渡槽進行地震響應分析。對渡槽橫向輸入7度人工地震波，觀察隔震支座對渡槽結構的隔振效果。地震波加速度按照《水工建筑物抗震設計規范》［8］標準設計反應譜擬合人工波，峰值加速度為0.1 g，特征周期Tg為0.2 s，地震持時10 s。本文不計結構靜力影響，單獨研究地震荷載下的結構動力響應。

表2為正常水位下設置隔震支座與不設置隔震支座時槽體關鍵部位的地震響應值。圖5為具體典型點的位移和應力的時程曲線。從圖表中可以看出，設置隔震支座后渡槽絕對位移增大，但渡槽跨中頂部與底部的相對位移、跨中頂部與跨端頂部的相對位移均下降顯著。渡槽結構的加速度降幅達56%，第一主應力、正應力也較非隔震時降低50%以上，整個渡槽槽體的地震響應明顯下降。以上分析可知：設置隔震支座后結構的地震動力響應得到了很大改善，隔震支座可以明顯降低結構的地震響應，從而使結構的抗震性能得到提高。

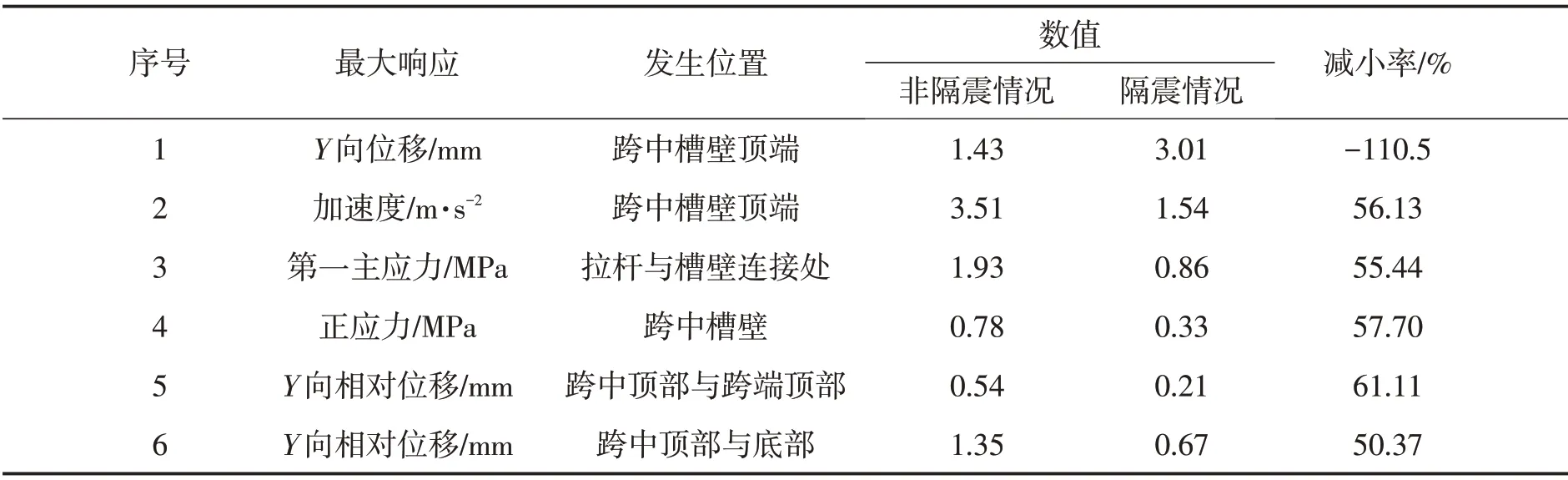
表2 結構地震響應值對比表Tab.2 Comparison of structural seismic response

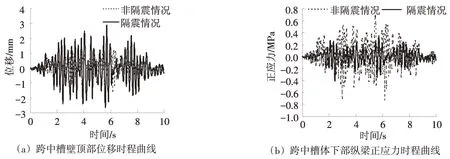
圖5 跨中槽體地震響應時程曲線圖Fig.5 Time history curves of seismic response

4 結語

1）建立了鉛芯橡膠支座的數值模型，采用有限元分析程序ADINA 模擬鉛芯橡膠支座的動態力學性能，得到的結果和實驗值大體吻合，驗證了分析理論和方法的正確性。因此可以利用有限元方法優化鉛芯橡膠支座的力學性能，通過改變橡膠厚度、鉛芯直徑等參數優選隔震支座，而不必進行多次昂貴的試驗。

2）分別對設置鉛芯橡膠支座的渡槽結構與不設置鉛芯橡膠支座的渡槽結構進行時程分析，結果表明：設置隔震支座后，槽體的加速度、應力狀況得到了很好的改善，地震響應明顯降低，結構的抗震性能得到明顯的提高。

3）設置鉛芯橡膠支座后槽體位移增大，但僅是鉛芯橡膠支座的大變形引起的，槽體跨中頂部與底部的相對位移、跨中頂部與跨端頂部的相對位移顯著減少。需要注意加強相鄰兩跨之間的止水等連接部位設計，可通過設置柔性連接、優化支座力學性能等方式減小相鄰垮的影響，保證槽體的安全。

［1］劉云賀，陳厚群.大型渡槽鉛銷橡膠支座減震機理的數值模擬［J］.水利學報，2003（12）：98-103.

［2］張艷紅，胡曉.大型渡槽隔震研究［J］.水利學報，2005，36（11）：1307-1313.

［3］熊世樹，周正華，王補林.鉛芯橡膠隔震支座恢復力模型的分析方法［J］.華中科技大學學報，2003，20（02）：28-31.

［4］葉志雄，李黎，聶肅非，等.鉛芯橡膠支座非線性動態特性的顯式有限元分析［J］.工程抗震與加固，2006，28（6）：53-56.

［5］朱伯龍，張琨聯.建筑結構抗震設計原理［M］.上海：同濟大學出版社，1994.

［6］曹宗楊，張撩軍.拱壩-庫水動力流固耦合作用的有限元數值研究［J］.水電能源科學，2013，31（4）：58-61.

［7］中國水利水電科學研究院，電力工業部昆明勘測設計研究院，電力工業部西北勘測設計研究院，等.SL203-97 水工建筑物抗震設計規范［S］.北京：中國水利水電出版社，1997.

［8］張漢云，張燎軍，李龍仲，等.水電站地面廠房鞭梢效應及抗震分析［J］.水電能源科學，2012，30（01）：92-126.

［9］高劍平，王斌，劉禮君，等.多層框架結構利用鉛芯疊層橡膠支座加層減震分析［J］.華東交通大學學報，2009，26（1）：1-6.