基于故障阻抗計算的非同步故障測距新方法

傅軍棟，李 澄，王 鍇，樊海全

（華東交通大學電氣與電子工程學院，江西 南昌330013）

在電力系統中，擔負電能輸送任務的高壓輸電線路發生故障最多，快速準確的故障定位對系統安全穩定和經濟運行十分重要。在電力工程界，輸電線路故障定位裝置的出現不但減輕了人工巡線勞動強度，而且使得測距更加精準［1］，在電力牽引網貫通線［2-4］中還存在故障測距適應性問題。因此，對故障測距領域進行更加快速、準確、靈活等方面的研究具有重要的實際意義。

輸電線路短路故障常有發生，考慮到電力系統運行方式變化及過渡電阻的存在會對單端量測距結果影響較大，文章主要研究在原理上不受上述影響的雙端量測距。雙端量法需要用到兩側的數據［5］，廣域測量系統中的PMU（phasor measurement unit，相量測量單元）可以提供兩側同步數據。然而，PMU優化配置滿足狀態觀測時可實現對全網的動態實時監控，即并非在全網所有廠站、母線都配置該裝置，且考慮到裝置失靈時必然存在兩端數據非同步，產生測距誤差。

迄今為止，國內外學者提出的雙端數據測量非同步的故障測距方法有限，主要有構造非線性方程［6-8］、估算非同步角［9］、消去不同步角［10］的3種方法。考慮到求解非線性方程時采用的迭代法收斂性和估算非同步角時估算誤差均具有不確定性問題，消去非同步角法就成了最有效可靠的方法。因此，主要研究如何消去非同步角來實現故障測距。

采用輸電線路集中參數模型，提出了基于故障阻抗計算的非同步故障測距新方法。該方法首先利用雙端電氣量求故障導納和故障阻抗，使得故障阻抗表達式中僅含故障距離一個未知量，并且在計算過程中巧妙地消去了非同步角影響，然后基于金屬性短路故障阻抗的純電阻性采用共軛法構造出以故障距離為未知量的一元二次方程，最后給出了偽根的判別方法，求解方程即完成測距。仿真結果表明該方法簡單易行，測距精度高，不受非同步角的影響，能適用于各種故障類型，魯棒性好［11］。

1 原理

1.1 線路模型

用單線圖表示經完全換位的單回輸電線路，線路發生單相接地短路故障如圖1所示。以母線S，R為始末端的線路全長為l，線路采用集中參數模型，單位長度阻抗為Z。兩端母線電壓和電流分別為US，IS和UR，IR，故障點F距離始端S距離為d，故障阻抗為ZF。

對于集中參數模型的輸電線路，依據電路基本原理，從始端S推算至故障點F的電壓UFS和末端R推算至故障點F的電壓UFR分別為

1.2 非同步電氣量校正

通常情況下，電氣量測量非同步是指測量裝置的時鐘誤差，誤差由裝置本身固有的缺陷而產生。雙端量法故障測距需要用到兩端的電壓、電流數據。在電氣量測量非同步時，利用這些數據進行計算得到的測距結果誤差較大，所以出于測距精度的考慮就必須對非同步電氣量進行校正。以始端時鐘為參考時刻，末端母線電壓和電流皆因非同步測量而變化，而線路單位長度阻抗Z和長度l則與之無關。以下對末端非同步測量的電壓和電流進行校正，記末端R側時鐘相對于始端S側時鐘的偏差為t，則非同步角δ=2πt/40=πt/20（40表示采樣頻率為2 kHz時一個周期的采樣點數）。由于δ=0就是同步測距的情況，因此非同步測距必然適用于同步測距。于是，校正后的末端R側的電壓和電流為

此時，校正后的從末端R側推算至故障點F的電壓為

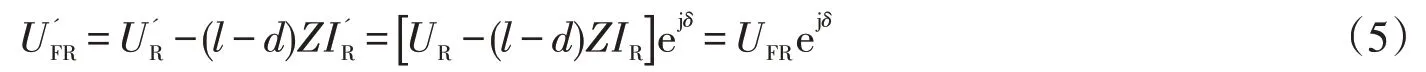
依據電路基本原理可知，從始端S側推算至故障點F的電壓UFS與校正后的從末端R側推算至故障點F的電壓相等，且都等于故障點電壓UF；從始端S側流入故障點F的電流IS與校正后的從末端R側流入故障點F的電流之和為故障電流IF：

1.3 故障阻抗計算

故障阻抗就是在故障點處故障相導線與地之間或者幾個故障相導線間發生的非正常連接的阻抗，可依據歐姆定律計算故障阻抗ZF。在故障點F處，由故障點電壓UF和故障電流IF可推得故障導納YF：

將（6）（7）代入上式，并結合（4）（5）可得（9）：

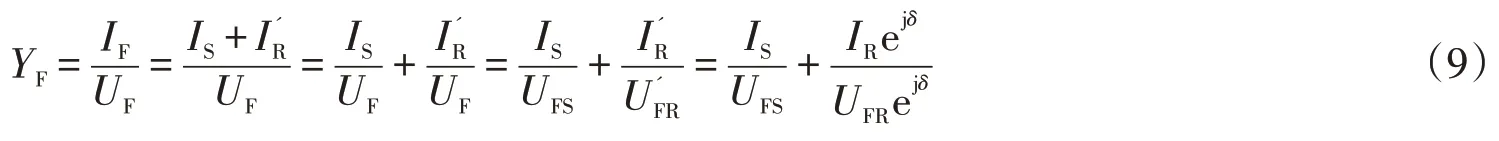
在電路分析中，用阻抗或導納表示歐姆定律是一種普遍形式。注意到阻抗和導納互為倒數，可由ZFYF=1得故障阻抗ZF：

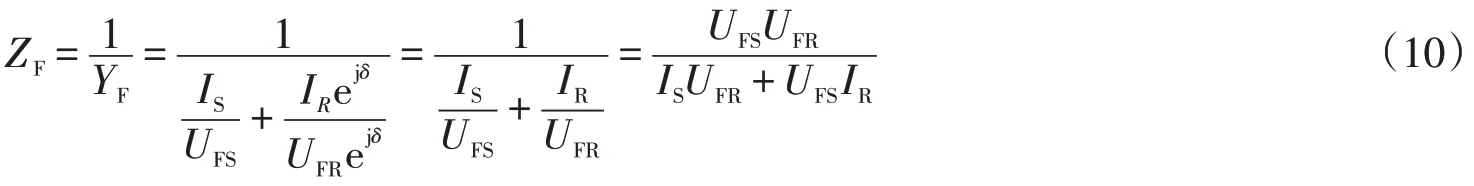
上式中ejδ≠0 恒成立，對ejδ的約分消除步驟有意義。從右端分式中看出故障阻抗計算表達式中不含ejδ，消除了非同步角的影響，因此（10）式可方便地用于非同步故障測距分析。故障阻抗計算表達式為分式，分別定義故障阻抗計算分子Q和故障阻抗計算分母W：

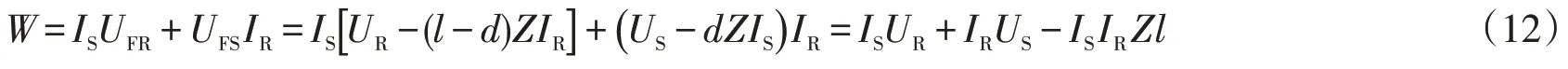
式中：Q的表達式系數A，B，C分別為：A=-Z2IRIS，B=USZIR-URZIS+Z2ISIRl，C=US(UR-ZIRl)。

從（11）和（12）可見，當雙端電氣量和線路基本參數一定時，Q是d的二次函數，W是常數。因此，故障阻抗ZF可以寫成（13）：

1.4 共軛法構造方程求d

系統中電氣量大部分用相量表示，而復數是相量分析方法的基礎，復數的代數形式為f=a+jb（其中，j=為虛單位，復數f的實部a=Re[f]，虛部b=Im[f]），其共軛復數為f*=a-jb。共軛法就是對方程等式兩邊同時取共軛復數形式以得到新的方程。發生短路故障時，故障阻抗通常情況為純電阻，其復數阻抗的虛部為零。對（13）兩邊取共軛復數，此時有故障阻抗的共軛復數與故障阻抗相等，即=ZF，則有（14）：

式中：W*為故障阻抗計算分母W的共軛復數；為UFS的共軛復數；為UFR的共軛復數；A*，B*，C*分別為故障阻抗計算分子Q的表達式系數A，B，C的共軛復數。

考慮到W和W*不為零，為不失一般性，聯立（13）（14）消去ZF，寫成適用于非零W和W*形式情況，即W*UFSUFR=，整理得（15）：

其中：

p=W*A-WA*；

q=W*B-WB*；

r=W*C-WC*；

A*=-Z*Z*；

B*=；

C*=；

W*=。

顯然p≠0 恒成立，方程（15）的解為

因此，僅需確定一元二次方程的各項系數p，q，r，就可以求得故障距離d，這里存在兩個解d1和d2，需要去除偽根。

1.5 偽根識別

首先注意到輸電線路的長度為l，其故障距離d必然滿足（17）：

其次，將解得的兩個解d1和d2分別代入（13）計算，可得到相對應的故障阻抗計算ZF1和ZF2，而實際故障阻抗值為ZF。雖然測量計算中不可避免的誤差會使計算值與實際值之間存在誤差，但是誤差不會太大。真實故障距離對應的故障阻抗計算值必然與實際值更為接近，故障阻抗計算值必然滿足（18）：

由（18）得到對應的兩個解d1和d2之一即為真根。至此，采用（17）（18）進行判別即可方便地去除偽根。

2 算法實現

采用包含于各種短路故障中的正序分量進行計算。因為線路兩端母線電壓和電流獲取容易，所以在線路參數已知時由前述原理可方便地確定一元二次方程的系數，進而求解方程實現測距。于是，測距差Δd=d-dS，測距誤差Δ：

式中：d為計算故障距離；dS為實際故障距離；l為線路全長。

至此，故障阻抗計算法的故障測距算法步驟如下：

1）開始；

2）輸入線路參數和長度l；

3）確定線路單位長度阻抗Z、始端電壓US、始端電流IS、末端電壓UR、末端電流IR及各自的共軛復數值Z*，，，，；按照式（11）計算故障阻抗分子Q的表達式系數A，B，C及其共軛復數值A*，B*，C*；按照式（12）計算故障阻抗分母W及其共軛復數值W*；

4）由步驟3中確定的各值計算一元二次方程方程（15）中的系數p，q，r并依據（16）計算故障距離d1,2；

5）按照（17）（18）判別偽根后得到故障距離真根d；

6）按照式（19）計算測距誤差Δ；

7）輸出故障距離d和測距誤差Δ；

8）結束。

3 仿真驗證

為驗證所提出的非同步測距新方法，參照雙端系統模型（如圖2），在PSCAD中搭建一條長為120 km的500 kV 的三相單回輸電線路進行仿真分析。表1 和表2 分別為系統參數和贛洪都—贛州500 kV 線路基本參數。

圖2 雙端系統模型Fig.2 Model of two-end system

表1 系統參數Tab.1 System parameters

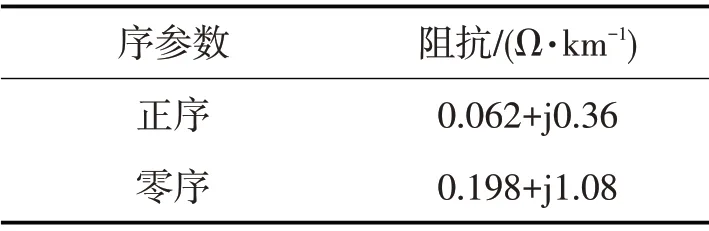
表2 輸電線路參數Tab.2 Transmission line parameters

3.1 單相接地短路故障測距

線路A相接地短路故障發生時刻為0.3 s，故障時延0.1 s。兩側系統中性點接點，故障電阻為10 Ω。仿真采樣頻率為2 kHz，利用故障后50 ms之內的數據進行測距計算。由于故障相兩側電壓和電流中含有基波、諧波分量和衰減直流分量，因此為克服衰減直流分量以及諧波分量的影響，采用測距精度較高的差分傅氏濾波算法進行濾波，由濾波后的數據按照對稱分量法計算各正序分量。最后，利用MATLAB按照本文提出的故障阻抗計算法進行編程與計算，即可求得故障距離d和誤差Δ。

3.1.1 非同步角對測距結果的影響

為了考察非同步角δ對測距結果的影響，當線路上不同地點發生單相接地短路故障時，計算出當δ在-180°到180°之間變化時采用故障阻抗計算法的測距結果（見表3）。

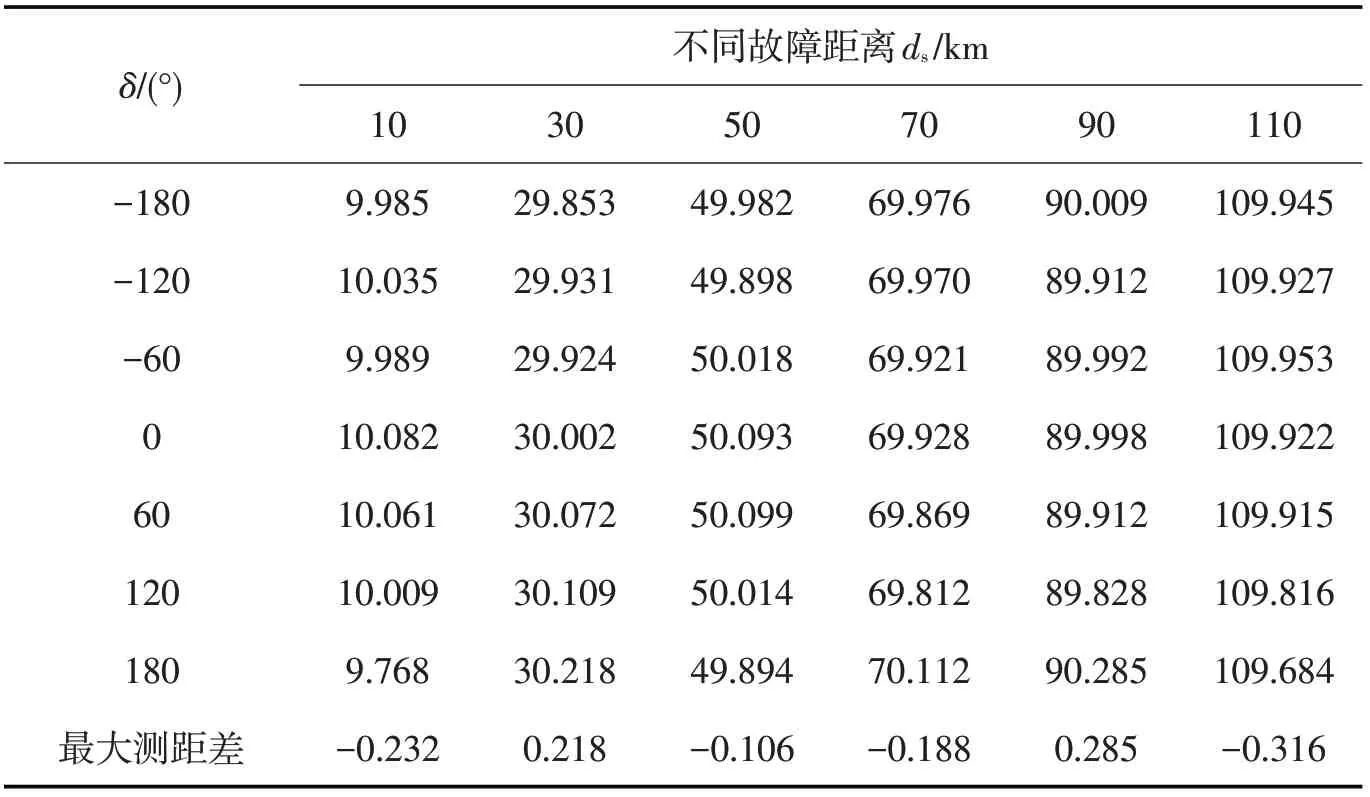
表3 非同步角對測距結果的影響Tab.3 The effect of unsynchronized angle to fault location result

從表3可以看出，120 km長的線路在10 km到110 km之間發生故障的最大測距差為-0.316 km，越靠近線路中間點時測距差越小，最小測距差為-0.106 km，非同步角δ對新方法測距結果影響甚微。

3.1.2 故障電阻對測距結果的影響

選取當δ=60°時線路不同故障距離dS發生單相接地短路故障，不同故障電阻Rg對應的測距結果如表4 所示。從表中可以看出，當故障電阻從100 Ω至500 Ω變化時，最大與最小測距差分別為0.210 km 與0.034 km，可見故障電阻對測距結果幾乎沒有影響。

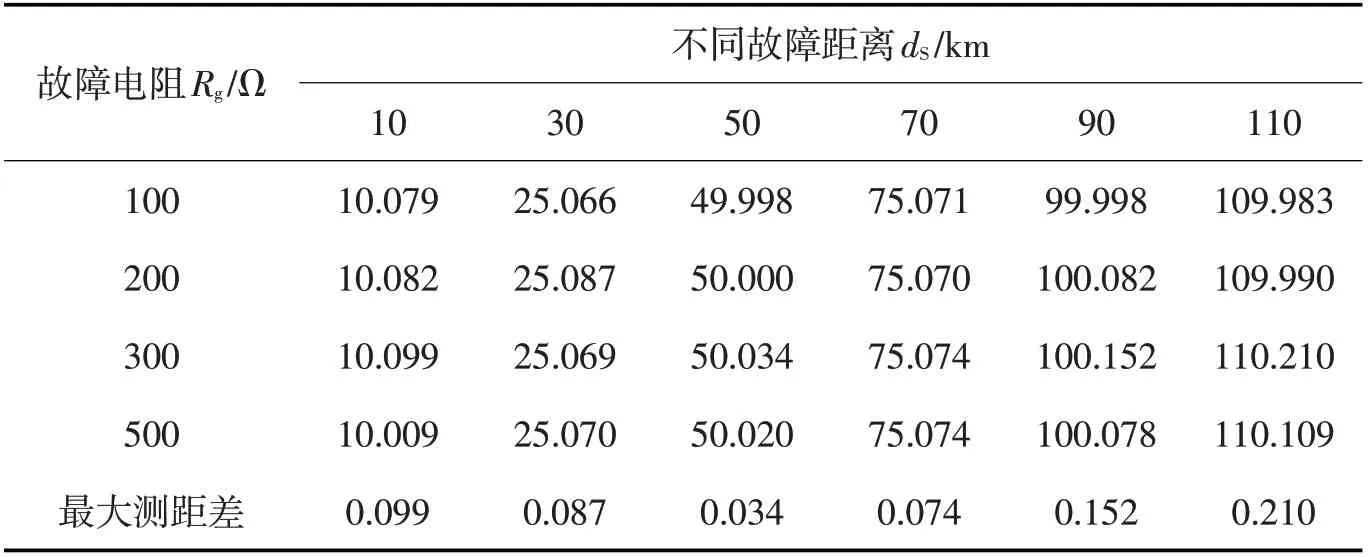
表4 不同故障電阻對測距結果的影響Tab.4 The effect of different fault resistance to fault location result

3.2 不同短路故障類型測距

參照前述單相接地故障測距步驟，分別對兩相接地、兩相短路、三相短路情況采用新方法進行計算。圖3 給出了對應于各短路故障在不同非同步角δ和不同故障距離dS的測距誤差Δ情況。從圖中可以看出，越靠近線路中點測距誤差越小，越靠近兩側誤差越大。從圖3（a）可以看出，單相接地短路最大測距誤差不超過0.27%；從圖3（b）可以看出，兩相接地短路最大測距誤差不超過0.5%；從圖3（c）可以看出，兩相短路最大測距誤差不超過0.5%；從圖3（d）可以看出，三相短路最大測距誤差不超過0.25%。由此可知三相短路測距誤差最小，新方法可以適用于各種短路故障。

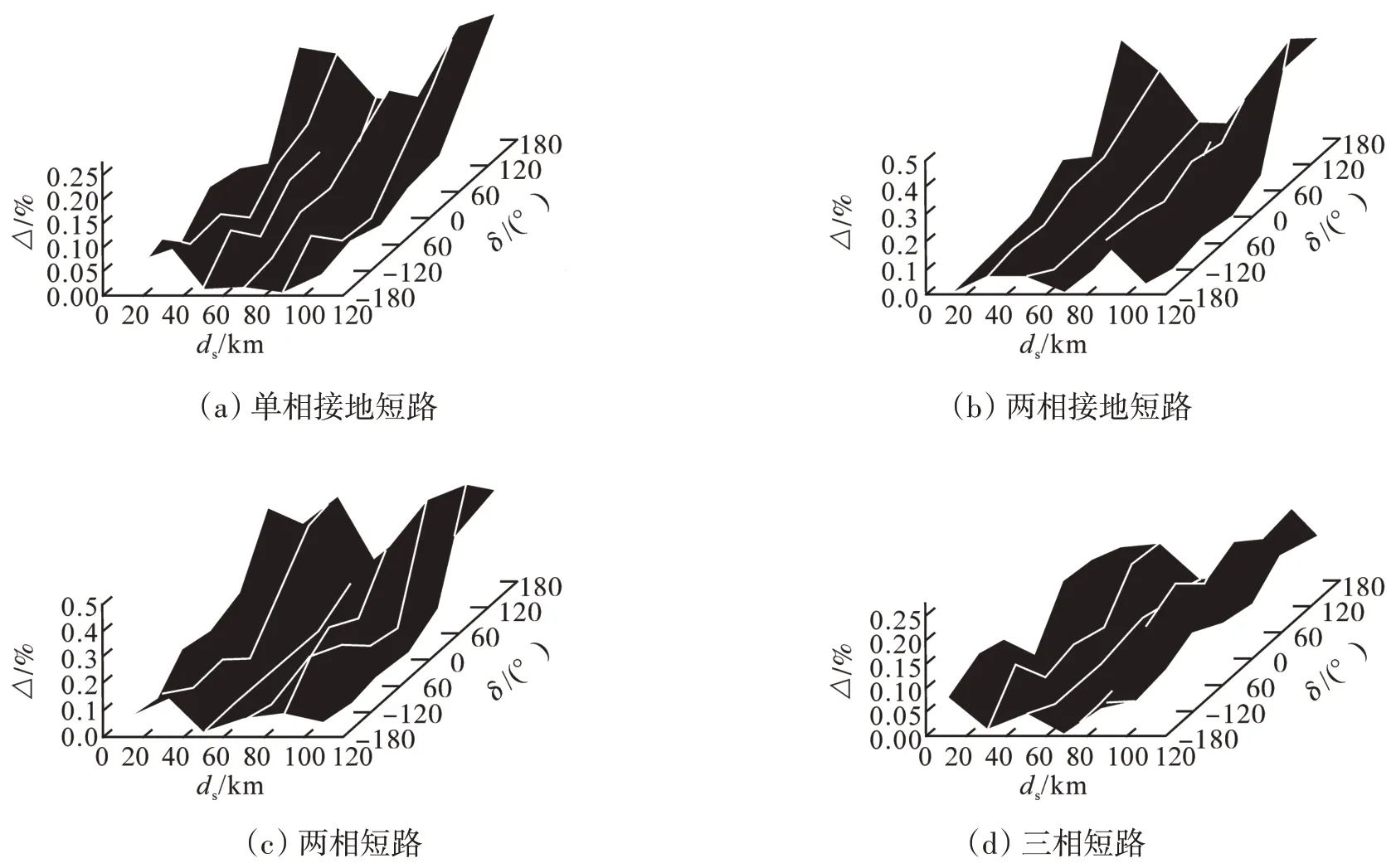
圖3 各種短路故障的測距誤差Fig.3 Fault location error of all short-current fault

4 結論

基于輸電線路集中參數模型提出了雙端測距新方法，適用于各種金屬性短路故障。該方法主要利用故障阻抗計算和共軛法構造了故障距離一元二次方程，該方程的求解與偽根判別方便。仿真表明該方法簡易可行，測距精度高，且不需要雙端數據同步。但是，該方法還存在不足之處，不能適用于非金屬性短路故障，具體方法有待進一步研究。

[1]葛耀中.新型繼電保護和故障測距的原理與技術[M].西安:西安交通大學出版社,2007:256-257.

[2]何人望.電力貫通線故障測距方法的適應性分析[J].華東交通大學學報,2003,20(1):16-19.

[3]邱萬英.一種電力貫通線單相接地故障測距的新方法[J].華東交通大學學報,2010,27(4):48-51.

[4]楊豐萍,王喜燕.AT供電牽引網故障測距仿真研究[J].華東交通大學學報,2012,29(5):34-37.

[5]MEKHAMER S F,ABDELAZIZ A Y,M EZZAT&T S.Abdel-salam.fault location in long transmission lines using synchronized phasor measurements from both ends[J].Electric Power Components and Systems,2012,40(7):759-776.

[6]徐鵬,王鋼.雙端非同步數據故障測距的非線性估計算法[J].繼電器,2005,33(1):16-20.

[7]蔣春芳,王克英.基于參數估計的雙端不同步故障測距算法[J].繼電器,2008,36(1):1-4.

[8]李勛,石帥軍,龔慶武.采用信賴域法和雙端非同步數據的故障測距算法[J].高電壓技術,2010,36(2):396-400.

[9]張愛楓.不需要雙端數據同步的工頻故障測距新方法[J].重慶大學學報,2003,26(8):78-81.

[10]施世鴻,何奔騰.基于分布參數模型的雙端非同步故障測距算法[J].電網技術,2008,32(9):84-88.

[11]陳錚,董新洲,羅承沐.單端工頻電氣量故障測距算法的魯棒性[J].清華大學學報,2003,43(3):310-313.