基于線性補償函數的機載雙基SAR二維頻譜研究

黃 歡

（中國民航飛行學院 模擬訓練中心，四川 廣漢 618307）

0 引言

機載雙基SAR 是將發射機和接收機放置在兩個不同的飛機平臺的靈活系統。由于在任意構型下，飛機運動模式和天線的照射模式存在多種的配置方式，已至于任意構型的機載雙基SAR 比傳統單基SAR 能夠得到更為廣泛的應用[1-2]。

二維頻譜解析表達式模型是機載雙基SAR 的高效成像技術基礎。然而，在推到二維頻譜時面臨著巨大的困難。雙基SAR 斜距史函數是由兩個不同的雙曲線函數的疊加，從而駐定相位時間點是四次方函數的根[3]，導致無法得到準確的根表達式。因此，無法直接利用駐定相位定理求解任意構型機載雙基SAR 二維頻譜。

為了避免求解四次方函數的根表達式，Loffeld[4-5]和Wang[6]先后提出分析由不同運動平臺產生的多普勒頻率比例關系來計算雙基SAR二維頻譜，然而忽略由于多普勒頻率的空變性帶來的成像算法的缺陷。對于特殊的雙基SAR 系統，上述空變性是無法忽略的，因此產生了新的問題。Liu 等提出一種二維頻譜解析模型，即Air-Phase 模型(AP 模型)[7]。但它存在的缺陷在于只能用于小斜視角下的系統[8]。為了得到適用于一般的雙基系統的二維頻譜模型，Neo[9]利用級數反演的方法等效求解駐定相位時間點得到雙基二維頻譜模型。雖然它能夠近似等效雙基SAR 二維頻譜，但是它的等效精度與表達式的復雜度成正比的。

本文提出了一種適用于任意構型的機載雙基SAR 的二維頻譜解析式模型，它是通過曲線擬合將斜距史函數等效為有利于利用駐定相位定理的函數得到的。首先采用曲線擬合方式將雙基SAR 斜距史等效為雙曲線-線性疊加函數。等效后的斜距史函數能夠方便地利用駐定相位定理得到最終的雙基SAR 二維頻譜解析式。對解析式分析得到，提出的二維頻譜模型精確且非常簡潔，并類似于單基SAR 的二維頻譜。最后通過仿真數據驗證了上述二維頻譜模型能夠很好地表示任意構型的機載雙基SAR。

1 基于線性補償函數的斜距史等效

任意構型的機載雙基SAR 斜距史表達式如式（1）所示。

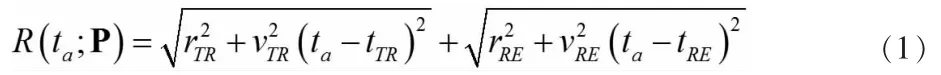
其中，向量P 代表參考點位置，rTR，vTR和tTR分別代表發射機最短斜距史、運動速度、零多普勒時刻，rRE，vRE和tRE代表接收機最短斜距史、平臺運動速度和零多普勒時刻。從（1）中可以看出，由于兩平臺是相互獨立的，導致雙基斜距史函數是兩個不同的雙曲線函數的和函數，因此，給駐定相位時間展開點的求解帶來了困難。

為得到簡潔的機載雙基二維頻譜解析式，將雙基斜距史函數等效為如下的表達式，即式（2）：

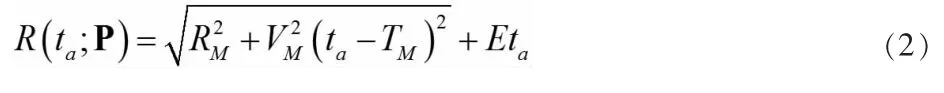
其中，RM、VM、TM分別是等效的最短斜距史、平臺運動速度和零多普勒時刻，M 代表單基平臺，E 表達誤差補償函數的系數。現通過泰勒公式將得到式（2）的泰勒級數表達式，如下所示。

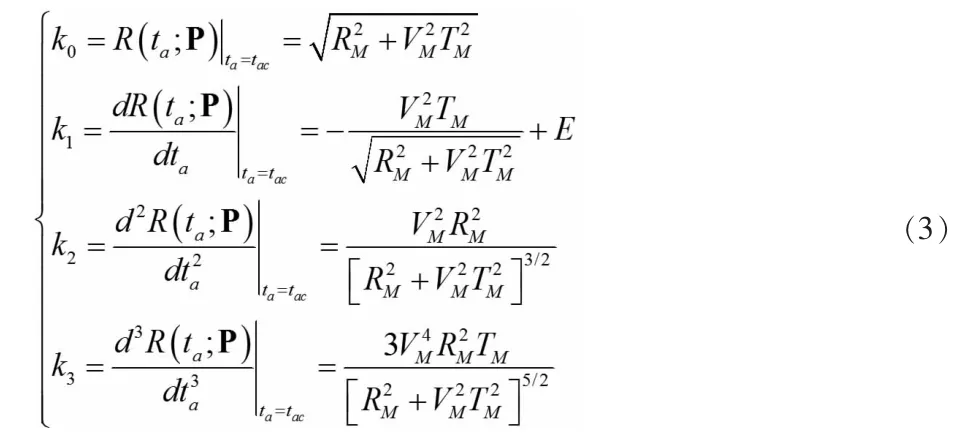
其中，ki，i=0，1，2，3 是關于方位向時間ta的i 階泰勒系數。通過一系列處理，式（3）中的系數可以得到：

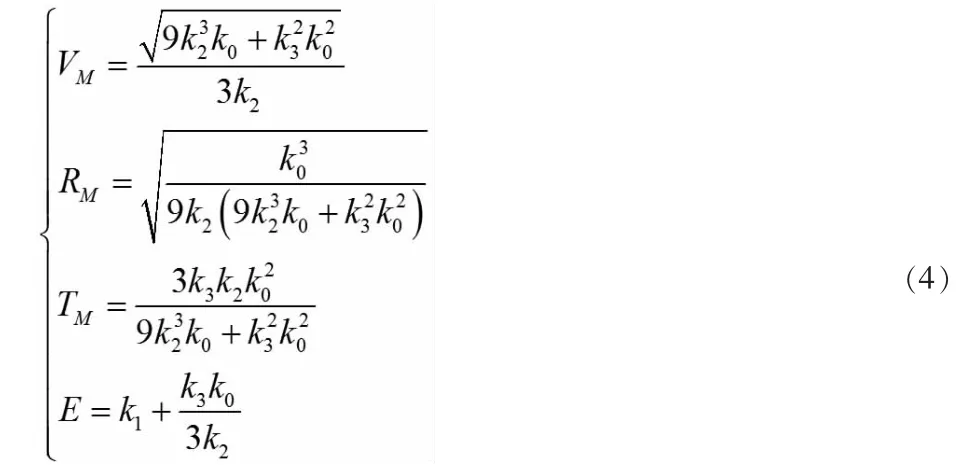
將式（4）帶入到式（2），能夠得到雙基斜距史函數。

2 二維頻譜解析式

通過式（2）～（4）和駐定相位定理，駐定相位展開時間點能夠得到：

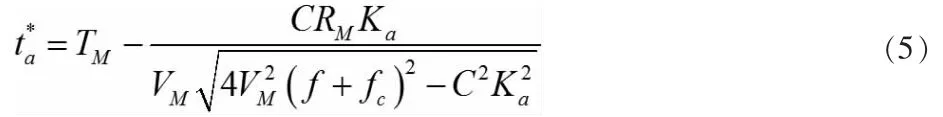
其中，Ka是等效的多普勒頻率，因此，二維頻譜解析式能夠表示為：

δ(·)是參考點的RCS。

分析式（7）發現，表達式形式類似于單基SAR 的二維頻譜形式。由于Ka是距離-方位耦合函數，因此它使得二維頻譜解析式能夠更加精確、簡潔。

3 仿真結果

為驗證上述二維頻譜的有效性，給出不同斜視角運動夾角的機載仿真結果。在整個仿真過程中，載頻fc=9.65GHz，帶寬B=100MHz，脈沖重復頻率PRF=800Hz，合成孔徑時間T=2s，其他相關參數如表1 所示。

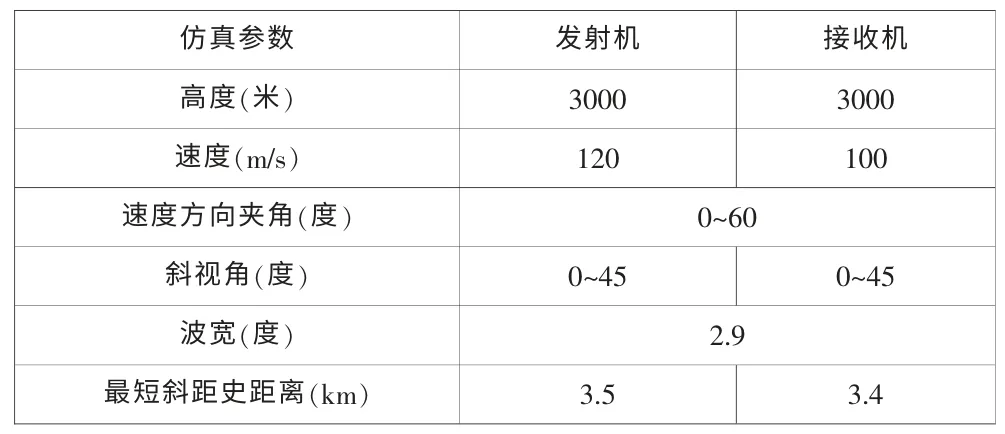
表1 系統參數Tab.1 System parameters

首先根據上述仿真參數，分析上述方法的斜距史等效誤差與CFA頻譜模型的斜距史等效誤差[10]之間的差別。其中，圖1 顯示兩種等效方式在斜視角(β)和平臺運動方向夾角(α)不同的情況下所帶來的斜距史等效誤差。

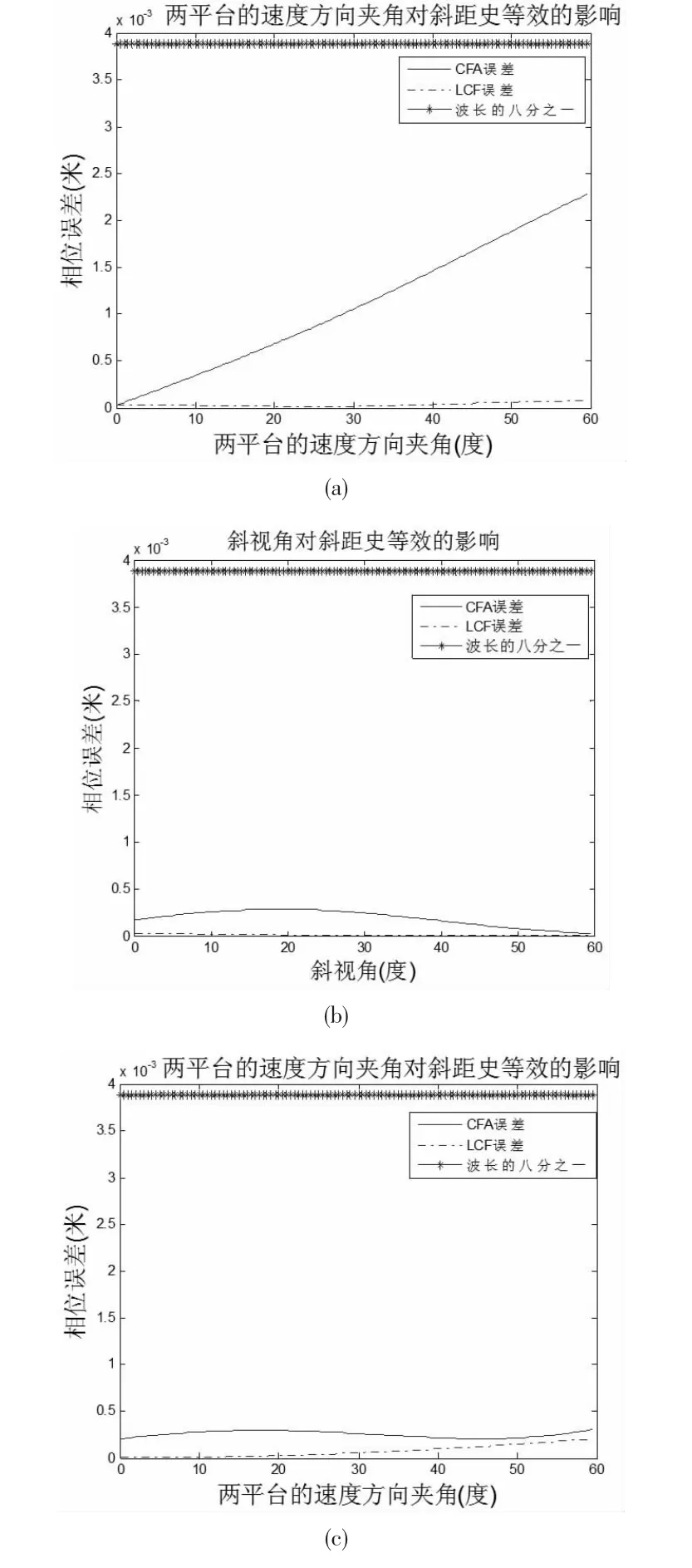
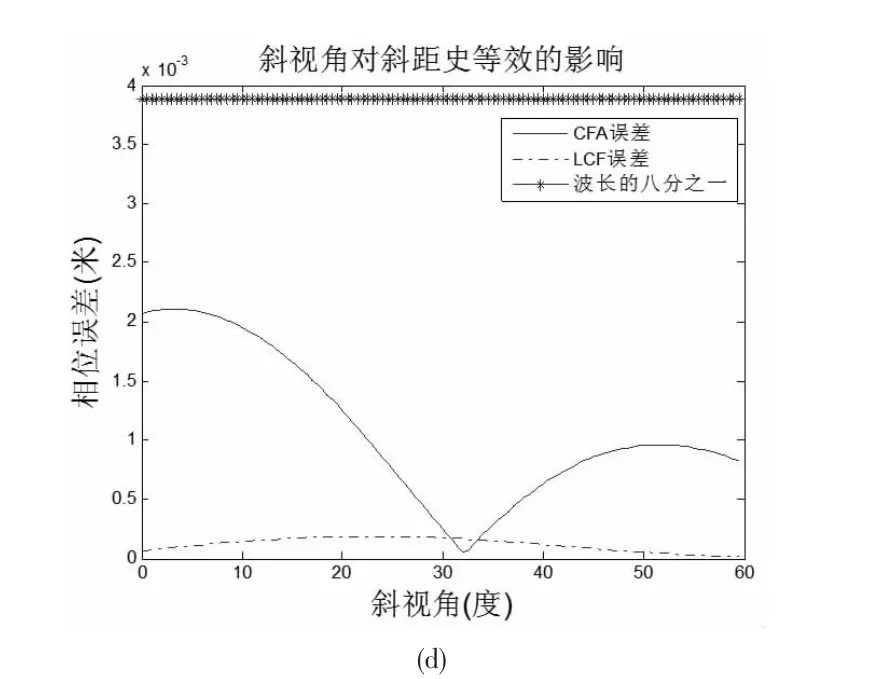
圖1 平臺運動方向夾角和斜視角變化對斜距史等效誤差的影響(a)β=0°,平臺運動方向夾角變化對等效斜距史誤差的影響(b)α=10°,斜視角變化對等效斜距史誤差的影響(c)β=30°,平臺運動方向夾角變化對等效斜距史誤差的影響(d)α=50°,斜視角變化對等效斜距史誤差的影響Fig.1 Influence on slant range history approximate error(SRHAE)with the variety of platforms’ motion and squint angle (a) whenβ=0°,Influence on SRHAE with the variety of platforms’ motion(b)whenα=10°,Influence on SRHAE with the variety of squint angle(c) whenβ=30°,Influence on SRHAE with the variety of platforms’motion (d) when α=50°,Influence on SRHAE with the variety of squint angle

雖然在圖1(d)中，在斜視角為30 度(β=30°)時，CFA 模型產生的斜距史等效誤差略小于上述方法產生的誤差，但是在不同的仿真情況下，本方法產生的斜距史等效誤差都要優于CFA 模型。從圖1 中也可以看出，兩種等效方式所產生的等效誤差都遠遠小于發射信號波長的八分之一，對點目標的聚焦不會產生任何影響[10-11]，因此說明上述方法的精確性和有效性。為進一步研究上述二維頻譜解析式的精確性，將從四種不同的平臺運動方向夾角和斜視角情況出發，分析參考點目標的聚焦效果。圖2 給出了四種情況下參考點目標補償上述二維頻譜后的聚焦結果。從圖2 中知道，參考點目標能夠得到很好的聚焦。為分析聚焦結果的性能，我們將利用3dB 面積和二維積分旁瓣比(2D-ISLR)作為評判標準[11]。其中，表3 給出四種情況下的聚焦性能。

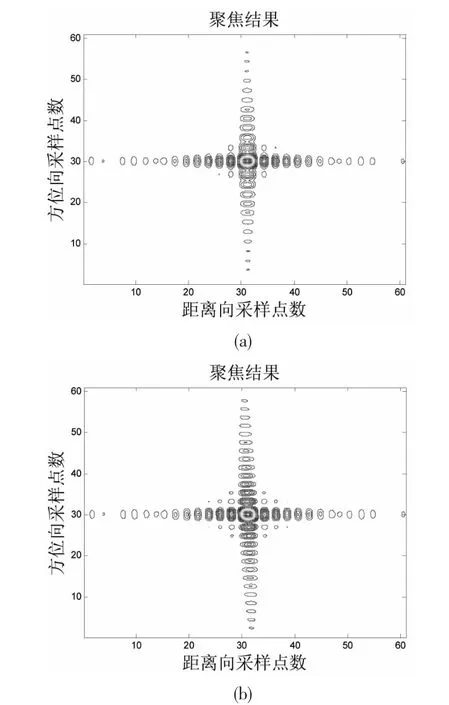
圖2 參考點目標聚焦結果(a)α=0°,β=0°(b)α=20°,β=15°(c)α=40°,β=30°(d)α=60°,β=45°Fig.2 The focus result of reference point targets(a)α=0°,β=0°(b)α=20°,β=15°(c)α=40°,β=30°(d)α=60°,β=45°

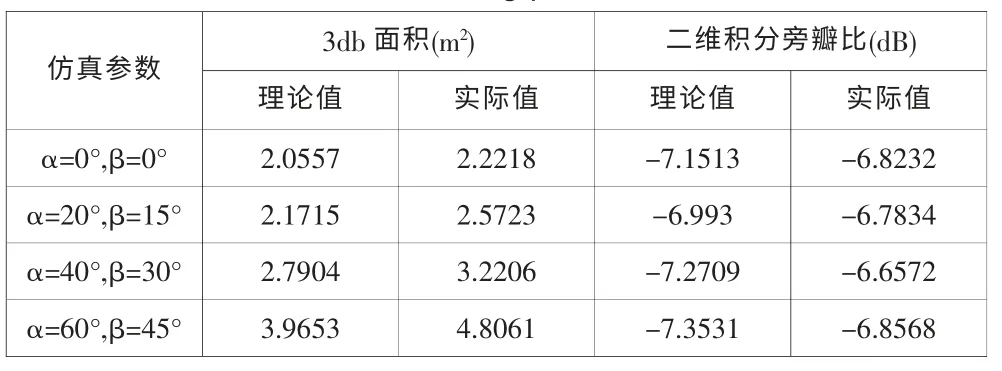
表2 聚焦性能Tab.2 Focusing performance

從表2 中可知，補償上述二維頻譜聚焦后，參考點目標的3db 面積和二維積分旁瓣比的實際值非常接近于理論值，說明上述二維頻譜的有效性和精確性。通過整個仿真結果說明采用上述的等效方法得到的二維頻譜解析式精確且簡潔，對之后的研究提供了良好的基礎。

4 結論

提出一種基于泰勒原理的斜距史等效方法，能將機載雙基二維頻譜斜距史等效為簡潔形式的表達式，從而方便地使用駐定相位定理求得二維頻譜解析式，而且由此求解得到的二維頻譜解析式簡潔且精確，為以后的成像算法的研究提供理論基礎。最后，通過對機載雙基SAR 的大量仿真，驗證了上述二維頻譜解析式的有效性。

［1］Ben Kassem M J，Saillard J，Khenchaf A.BISAR mapping I.Theory and modelling[J].Progress In Electromagnetics Research，2006，61:39-65.

［2］Schlund M，von Poncet F，Hoekman D H，et al.Importance of bistatic SAR features from TanDEM-X for forest mapping and monitoring [J].Remote Sensing of Environment，2013.

［3］Clemente C，Soraghan J J.Bistatic slant range approximation using Chebyshev Polynomials[C].Radar Conference (RADAR)，2011 IEEE.IEEE，2011:789-792.

［4］Loffeld O，Nies H，Peters V，et al.Models and useful relations for bistatic SAR processing[J].Geoscience and Remote Sensing，IEEE Transactions on，2004，42(10):2031-2038.

［5］Ul-Ann Q，Loffeld O，Nies H，et al.A point target reference spectrum based on Loffeld’s bistatic formula (LBF) for hybrid configurations[C].Emerging Technologies，2008.ICET 2008.4th International Conference on.IEEE，2008:74-77.

［6］Wang R，Deng Y K，Loffeld O，et al.Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase [J].Geoscience and Remote Sensing，IEEE Transactions on，2011，49(10):3504-3520.

［7］Zhe L，Jian-yu Y，Xiao-ling Z，et al.An approximated analytical solution for two-dimensional spectrum of spaceborne/airborne hybrid bistatic SAR[C].Communications，Circuits and Systems，2007.ICCCAS 2007.International Conference on.IEEE，2007:822-825.

［8］Liu Z，Yang J，Zhang X，et al.Frequency domain imaging algorithm for spaceborne/airborne hybrid bistatic SAR [C].Geoscience and Remote Sensing Symposium，2007.IGARSS 2007.IEEE International.IEEE，2007:842-845.

［9］Neo Y L，Wong F，Cumming I G.A two-dimensional spectrum for bistatic SAR processing using series reversion[J].Geoscience and Remote Sensing Letters，IEEE，2007，4(1):93-96.

［10］Huang H，Zhang X，Liu Z.A SIMPLE REFERENCE POINT SPECTRUM MODEL AND MODIFIED OMEGA-K IMAGING ALGORITHM FOR SPACEBORNE/AIRBORNE BISTATIC SAR，Geoscience and Remote Sensing Symposium(IGARSS)，2013 IEEE International.IEEE，2013:2497-2500.

［11］Dai C Y，Zhang X L.Omega-K algorithm for bistatic SAR with arbitrary geometry configuration[J].Journal of Electromagnetic Waves and Applications，2011，25(11-12):1564-1576.