物理實驗與測量不確定度

楊海平

（烏恰縣質量技術監督局 質量與計量檢測所，新疆 烏恰845450）

1 不確定的概念

“不確定度”一詞是指可疑、不能肯定或測不準的意思,不確定度是測量結果所攜帶的一個必要的參數,以表征測量值的分散性、準確性和可靠程度.不確定度反映了可能存在的誤差分布范圍,即隨機誤差分量和未定系統誤差分量的聯合分布范圍.一個完整的測量結果不僅要給出該量值的大小(即數值和單位),同時還應給出它的不確定度,用不確定度來表征測量結果的可信賴程度.于是測量結果應寫成下列標準形式:x=x±U(單位）Er=U/x×100%式中x 為測量值,對等精度多次測量而言,x 為多次測量的算術平均值;U 為不確定度,Er 為相對不確定度.

2 不確定的分類和評定方法

測量不確定度通常由幾個分量構成,按數值的評定方法不同可將分量分為A 類和B 類.A 類分量是指在同一條件下多次重復測量時由一系列觀測結果用統計方法計算的分量,用符號“UA”表示.B 類分量是指用非統計方法計算的其他分量,用符號“UB”表示.測量不確定度有三種定量表達方式:①標準不確定度:用標準偏差表示的測量結果的不確定度.②合成標準不確定度:由若干標準不確定度合成的不確定度.③擴展不確定度:用包含因子k 乘以合成標準不確定度,得到擴展不確定度,這樣可以得到一個區間的量,該區間包含了合理賦予的被測量值分布的大部分. 它將合成標準不確定度擴展了k 倍, 從而提高了置信水平。

2.1 直接測量的不確定度的評定

2.1.1 單次直接測量的標準不確定度的評定

在物理實驗中經常遇到單次測量的情況.原因是多次測量時A 類不確定度遠小于B 類不確定度,或物理過程不能重復,因此無法多次測量.在一般情況下,簡化的做法是采用儀器誤差,作為單次測量的不確定度的估計值.故U=UB（x）=Δ儀

2.1.2 多次直接測量的標準不確定度的評定

多次直接測量的A 類標準不確定度的評定

在相同條件下,對某一物理量x 進行n 次等精度獨立測量,其測量值分別為x1，x2，…，xn則該測量值的最佳估計值為算術平均值,即：

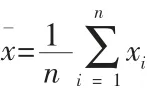
在這種情況下,單次測量的標準偏差Sx由貝塞爾公式得到：

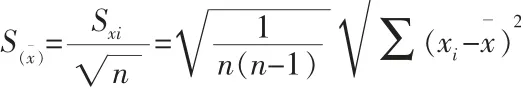
由于多次測量的平均值比一次測量值更準確,隨著測量次數的增多,平均值收斂于期望值.因此,通常以樣本的算術平均值作為被測量值的估計(即測量結果),以平均值的標準偏差S（xˉ）作為測量結果的標準不確定度即A 類標準不確定度所以：

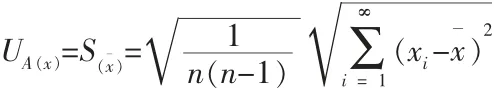
（1）這里直接把S（xˉ）作為A 類標準不確定度uA（xˉ）,測量次數不是很少時,對應的置信率為68.3%,當測量次數不太多(教學實驗測量中均為有限次測量,一般只有5-10 次),這時測量結果偏離正態分布,而服從t分布.則A 類不確定度分量uA（xˉ）由S（xˉ）乘以因子tp求得,即：

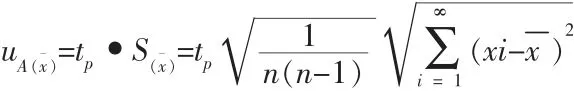
（2）多次直接測量的B 類標準不確定度的評定

在物理實驗中,B 類標準不確定度的數值主要來自以前的測量數據,對有關技術資料和測量儀器特性的了解和經驗,技術說明書或其他證書以及手冊等提供數據.若已知B 類分量誤差的極限,則B 類不確定度為

在缺乏信息難以分清分布的情況下,以不確定度偏大假設為準,一律按均勻分布處理.即：

（3）多次直接測量的合成標準不確定度的評定按方和根合成原理可以得到直接測量的合成不確定度公式,即：

2.2 間接測量不確定度的評定——不確定度的傳遞與合成

設間接測量量y 可寫成直接測量量x1，x2，…，xn的函數y=f（x1，x2，…，xn）.則間接測量y 的最佳值為y=f(x1，x2，…，xn) .由誤差的全微分表達式：

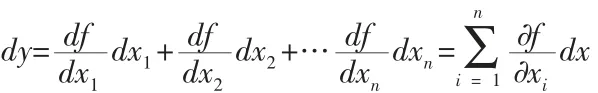
?(其中dy,dxi分別為y 及xi 的誤差),從誤差傳遞的代數和式可以導出標準偏差的方和根合成,即：

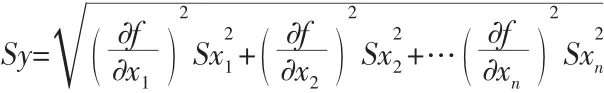
（4）式中Sy 為間接測量量的標準偏差;Sxi為直接測量量的標準偏差.在各量X1，…，Xn互相獨立的前提下,式（4)的標準偏差傳遞公式在數學上是嚴密的. 人們公認Uy為以標準偏差形式表示的不確定度,其傳遞公式形同標準偏差的形式,也是各分量與偏導數之積的方和根,于是得到間接測量的總不確定度的近似公式為：

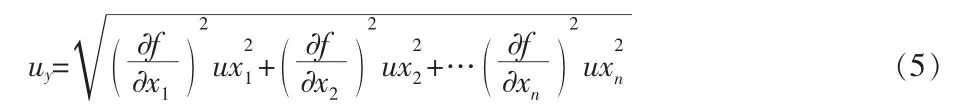
不確定度的概念和體系是現代誤差理論發展的基礎上建立和完善的,是對測量結果評定和表示國際標準化和規范化的重要體現.掌握不確定度的概念,應作為物理實驗的基本要求,這是物理實驗內容改革的一個重要環節.

［1］董有爾,張天喆.近代物理實驗[M].北京:科學出版社,2006:44-55.

［2］朱鶴年.物理實驗研究[M].北京：清華大學出版社,1990:12-43.

［3］JJF1059-1999 國家質量技術監督局.測量不確定度評定與表示[S].中國計量出版社,1999.