科恩否定原理的局限及其嘗試性修正

李 鐵，張大松

(1.武漢商貿職業學院通識教育學院，武漢 430205;2.華中師范大學 馬克思主義學院，武漢 430079)

科恩否定原理可表述為:對于任何E和H，如果E報道物理上可能的一個事件或一些事件或一個合取式，那么，如果 S［H，E］＞0，則 S［﹁H，E］=0［1］177。在批判數學概率邏輯的局限性基礎上，科恩否定原理體現出自身的理論價值和應用價值，但它本身仍然存在一定的局限性，這種局限性表現為理論自身的不一致性和應用上的不恰當性。其根本原因在于否定原理采取了過強的否定策略。

一、科恩否定原理的實質

科恩的否定原理可表述為，任一命題H被賦值大于零級的支持等級時，否定H只能獲得零級的支持等級。科恩給出了如下的證明:對于任一全稱量化條件命題

(1)?x(Rx→Sx)，它的否命題為

(2)?x(Rx∧﹁Sx);

由于(1)或蘊含(1)的命題得到了成功檢驗，故可對它指派大于零的支持等級。但是由于(2)不是全稱量化條件命題，因而它不可檢驗并指派支持等級，它的支持等級只能從蘊含它的命題的檢驗結果而獲得。但這一結果必定是零。例如，如果

(3)?x(Fx→Kx)

(4)?x((Fx→Kx)→(Rx∧﹁Sx))

都能得到有力檢驗結果，那么就能分別通過合取原理和后承原理得到，(3)和(4)的合取所具有的歸納支持至少與(2)的支持等級一樣。因為(2)是這一合取式的后承。但是，我們又可知，(4)所通過的檢驗一定是(1)未能通過的;如果(1)具有正支持等級，那么就不可能通過檢驗以間接的方式確立(2)的正支持等級。所以(2)的支持等級不可能大于零。證畢［1］177－178。

否定原理實際上要表明的是，如果假說H基于證據E得到了大于零級的支持，那么基于同樣的證據就不能對它進行否定，同時基于同樣證據的其他假說相對于H不具有競爭地位。它有著深刻的內涵。首先，在性質上，它表明歸納概率邏輯的句法結構與數學概率邏輯的句法結構不可通約。在數學概率中，否定原理是互補的，即Pr(﹁p)=1－Pr(p)，而在歸納支持中，否定原理不具有這種減法性質，是非互補的。因此歸納支持是一種不同于數學概率的獨立的邏輯句法。其次，在方法論上，它強調不同權重的證據對假說的歸納支持等級的影響。這種測度是通過相關變項法得以實現的。第三，它體現了局部支持的思想，當假說基于背景知識得到大于零級的支持時，那么它不能被否定。否定原理是科恩理論最具特色的規則，同時也是科恩整個理論體系的基石，但它在理論和應用方面卻存在一定的局限。

二、科恩否定原理的局限性

科恩否定原理的局限性主要體現在理論內部及其推廣應用上。理論上的局限，主要是否定原理會導致系統內的邏輯矛盾。應用上的局限主要是否定原理對假說保護過強，拒斥競爭假說的合理性，不符合科學實際。導致這種局限性的主要原因是否定原理過強的否定性。

理論內部的非一致性體現在如下兩種情況中。

情況1 科恩在給出否定原理的證明后即設想:假設假說H1基于證據E得到大于零級且不完全的歸納支持，同時H2由于解釋了H1中反常的E，故 H2→﹁H1，且 H2的支持等級大于 H1，令:

(1)S［H1，E］＞ i/n+1，S［H2，E］＞ j/n+1，(n＞j＞i＞0)

(2)由否定原理，可得:S［﹁H1，E］=0;

(3)由 H2→﹁H1和后承原理，可得:S［﹁H1，E］≥ S［H2，E］＞0;

(4)因此(2)和(3)矛盾。

對于這一矛盾，科恩認為因為邏輯推論是正確的，又沒有理由對相關變項提出質疑，那么一定是相關變項集的排序出了問題，因此重新對相關變項集的序列進行考察可以解決矛盾。但科恩的這個理由與其歸納支持邏輯的整體思想相沖突。在科學實際中，科學家對相關變項集的排序是審慎的，變項的證偽能力同樣是依據經驗和已被科學共同體接受的背景知識確定的，如果一出現矛盾就修正相關變項集，無疑會使科學實踐遷就于邏輯定理。科恩在此陷入了自相矛盾，一方面堅持經驗主義原則，一方面又使經驗讓步于邏輯規律;更重要的是，它與歸納概率邏輯的局部支持宗旨相悖。

情況2 設H1和H2屬于同一競爭假說集，令S［H1，E］＞ i/n+1，S［H2，E］＞ j/n+1。

(1)由否定原理得:S［﹁H1，E］=0，S［﹁H2，E］=0;

(2)由析取原理得:S［H1∨﹁H1，E］=i/n+1，S［H2∨﹁H2，E］=j/n+1;

(3)由二值邏輯排中律得:H1∨﹁H1=1，H2∨﹁H2=1;因此(H1∨﹁H1)?(H2∨﹁H2);

(4)由齊一性原理和(3)得:S(H1∨﹁H1，E)=S(H2∨﹁H2，E);

因此(2)和(4)矛盾。

科恩雖然利用后承原理對這一矛盾提出自己的辯護，但已被證明他的反駁仍然是無效的。同時有學者認為，導致矛盾的根本原因在于相關變項法的語義解釋與經典二值邏輯的語義解釋之間存在矛盾。經典二值邏輯要求在同一思維過程中必須遵循排中律，但是相關變項法允許H和﹁H同時為零。這樣的批評是合理的，但這樣一來就要對二值邏輯的語義解釋和相關變項法的語義解釋同時做出修正，這樣不僅使邏輯系統的修改代價過大，而且亦不能解決情況1中出現的矛盾。

科恩否定原理在應用上的不恰當性主要指基于同樣的證據否定原理不承認競爭假說的地位，即假說H一旦得到某種程度的歸納支持，那么同樣的證據E不支持﹁H獲得大于零級的支持。結合物理學史上著名的光本性實驗，可以更直觀地發現否定原理在應用上的不恰當性。

光的本性論在歷史上曾有兩種觀點，惠更斯首先提出波動說，隨后牛頓提出粒子說。由于牛頓在當時的影響巨大，因此多數人支持光的粒子說。到底光的本質是粒子的還是波動的?科學家們設計了這樣的實驗，使光在兩種不同的介質中傳播，觀察光從一種介質到另一種介質時發生的情況。實驗以空氣和玻璃作為兩種不同的介質，結果顯示，光從空氣到玻璃面時既發生了反射又發生了折射。牛頓對此的解釋是，光的這種既反射又折射“痙攣”是由以太傳遞給粒子的。惠更斯則用幾何學理論解釋了光的反射和折射。這一實驗表明，基于相同的證據，相互競爭的假說都可得到一定程度的支持，甚至是相同等級的支持。但顯然科恩的否定原理與該實驗不符:首先通過相關變項法，可得粒子說和波動說的歸納支持等級，其中相關變項只有一個——光傳播的介質，變素只有玻璃 v1，R表示“是光”，S表示“是粒子”，F表示“是波”。

對于粒子說H1有:

(1)S［?x(Rx→Sx)，?x(Rx∧Sx∧T1x)］=1/2

(2)S［?x(Rx→Sx)，?x(Rx∧Sx∧T2x∧v1)］=2/2

因此，S［H1，E］≥2/2。

對于波動說H2有:

(1)S［?x(Rx→Fx)，?x(Rx∧Fx∧T1x)］=1/2

(2)S［?x(Rx→Fx)，?x(Rx∧Fx∧T2x∧v1)］=2/2

因此，S［H2，E］≥2/2。

根據否定原理，S［H1，E］＞ 0，那么 S［﹁H1，E］=0;又 H2→﹁H1，可根據后承原理得 S［H2，E］＜0。同理可證S［H1，E］＜0。可見否定原理在此自相矛盾，它與科學實際不符。

綜上所述，科恩系統的不一致性和應用的不恰當性都與否定原理有關，因此有必要考察否定原理本身的合理性。

否定原理存在局限性的主要原因是采取了過強的否定策略。所謂過強的否定策略是指由于堅持了二值邏輯的矛盾律，導致歸納支持的弱肯定性與矛盾律的強否定性不協調。通過分析科恩對否定原理的證明，可以發現這種不協調性。

科恩否定原理可以用一個蘊含式表示:(S［H，E］＞0)→(S［﹁H，E］=0)，該蘊含式前件體現了科恩的歸納支持思想，蘊含關系即為科恩的否定規則，后件為否定規則的結論。在科恩那里，全稱條件句假說H的支持等級是通過對特稱命題的逐級檢驗確定的，其推理模式為(T表示假說通過的實驗檢驗):

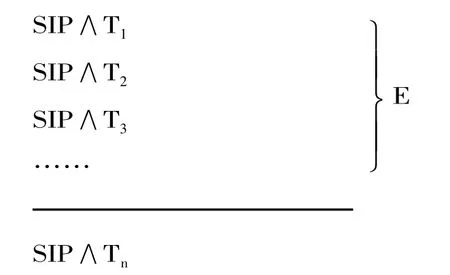
SIP與 SAP為差等關系，從 SIP不能必然推出SAP，因此SAP獲得的支持等級是歸納的。又SOP(﹁SAP)為特稱命題，其支持等級不可通過直接檢驗確定，而只能通過檢驗SEP間接地確定。因為SIP與SEP為矛盾關系，SIP通過的檢驗必然是SEP無法通過的，所以SEP的支持等級必然為零級。可見，否定原理是以歸納推理和矛盾律為邏輯內核的，依據前者全稱命題H獲得大于零級的支持等級，依據后者﹁H只能得到零級的支持。正因如此，科恩的否定原理在整體的邏輯性上出現了弱肯定與強否定的不協調，這種不協調性也必然會導致科恩整個邏輯系統的不一致性。事實上，從二值邏輯的觀點看，當S［H(SAP)，E］＞0時，即 S［H，E］的實質為 SIP，那么，S［﹁H，E］則為SOP，顯然，S［﹁H，E］不必然為零。正是因為科恩采取了不協調的邏輯規則，使得否定原理在應用中出現“怪論”，即SIP成立時，SOP不成立。

科恩否定原理在邏輯上的不協調也必然導致語義解釋上與實際不符。科恩否定原理在語義解釋上，不允許相同的證據對競爭假說都給予大于零級的支持，而在證據理論中，同一證據可以支持不同的假說。證據的基本特征為語句性、經驗性和相關性。證據語句在不同的語境下，可以有不同的指稱，其相關性也隨之變化。對于同一領域的競爭假說，證據都可起到相應的支持作用，這種支持作用既可能體現為對競爭假說提供不同程度的支持(甚或相同程度的支持)，也可能體現為對競爭假說不同部分的支持。因此在科學實際中，允許相互矛盾的假說并存。而科恩通過嚴格的矛盾律，拒斥了競爭。雖然這對假說給予了最大程度的保護，但不符合科學實際。

綜上，科恩否定原理內部存在弱肯定與強否定之間的矛盾，它必然導致系統的非一致性和不恰當性。要消除這種矛盾，必須對否定原理進行相應的修正。

三、科恩否定原理的嘗試性修正

科恩否定原理弱支持與強否定間的矛盾可以通過兩種途徑來調和，一是保留強否定，對弱支持進行加強修正;另一方法是，保留弱肯定，對強否定采取相應的弱化。考慮到科恩體系的整體特點以及它的理論和實踐價值，第一種途徑將使得科恩的系統更為復雜，其結果將不利于局部辯護，因此本文采取了第二種策略來修正科恩的否定原理。

科恩的歸納支持體現了局部辯護的思想，但是科恩并沒有對局部支持進行定量研究，只是考察某一S是P成立的條件，從而推出在同樣條件下所有S是P，這樣的支持太弱了，因為它不能保證在同樣條件下所有S是P。進一步的，他否定了在同樣條件下有S不是P的可能性。因此，在維護局部支持的前提下，應該對整體否定進行弱化。另一方面，在科學實際中，允許矛盾的存在，因此為了使歸納概率邏輯具有更好的應用推廣性，應當在放棄排中律的同時，也放棄矛盾律。基于這樣的考量，可以在三值邏輯的框架下對否定規則進行修正。

科恩的邏輯系統是一個等級系統，這與次協調邏輯的等級序列有共性。就是說，任一命題的歸納支持都是依靠相關變項的證偽等級來確定的，那么相應地，對它的否定也應該具有這樣的等級性。同時，由于次協調邏輯不嚴格遵守二值邏輯的矛盾律，因此它的真值允許有第三值(如表1所示)。

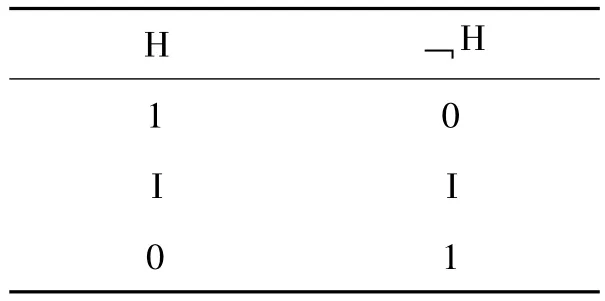
表1 真值表

但是在科恩邏輯系統中，任一命題都可通過實驗檢驗確定它的支持等級，因此H不取I，它可取［0，1］之間的值。這樣我們可以重新構造歸納概率邏輯的真值表，如表2(α表示H的取值)。

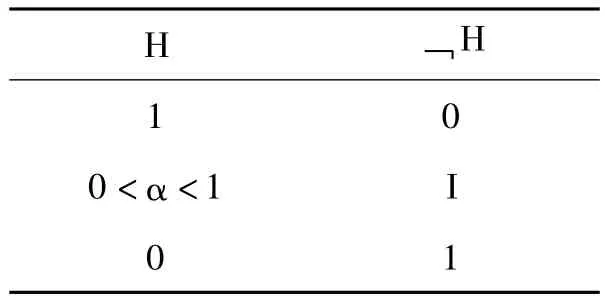
表2 真值表

由此，在歸納概率邏輯中任一命題H的值可以有3種情況，其中復合命題的賦值規則遵守三值邏輯的運算規則。在這一框架下，可對否定原理作出修正:

(1)S［H，E］=1 時，S［﹁H，E］=0

(2)0＜S［H，E］＜1 時，S［﹁H，E］=I

(3)S［H，E］=0時，S［﹁H，E］=1

由于歸納支持的相關變項法對相關變項集合不假定完全的樣本空間，它是一個開放的集合，允許任何時候當新的相關變項被發現時進入到該集合中，因此H的歸納支持等級在事實上永遠無法取到1，這樣修正方案(1)可去除。當S［H，E］=0時，說明假說H在經驗中無法被觀察到，也無需設計實驗來檢驗，修正方案(3)可去除。因此修正后的否定原理可表述為:對于任何E和H，如果E報道物理上可能的一個事件或一些事件或一個合取式，那么，如果 S［H，E］＞0，則 S［﹁H，E］=I。

科恩否定原理經三值邏輯框架的修正，會具有多方面的意義。

第一，它放棄了矛盾律和排中律，這樣相關變項法的語義解釋和三值邏輯的語義解釋相調和。鞠實兒教授在對科恩系統進行批判時，指出科恩系統的不一致性和不恰當性的根本原因在于相關變項法的語義解釋和二值邏輯語義解釋相矛盾。修正后的否定原理以三值邏輯為框架，其語義解釋也具有三值性，即:(1)一個可檢驗命題H具有j(j＞0)級的歸納支持等級，當且僅當它在至少有一可能世界Wj中為真;(2)當H具有j(j＞0)級的歸納支持等級時，其否命題﹁H具有不確定的歸納支持等級，亦即不能確定﹁H在任何可能世界Wj中必假。

第二，否定原理弱肯定與強否定之間的矛盾得以調和，使得歸納概率邏輯系統本身更加一致，在應用上也更加恰當。可考察上文情況2在否定原理修正后的情形。設H1和H2屬于同一競爭假說集，令 S［H1，E］＞ i/n+1，S［H2，E］＞j/n+1。

(1)由否定原理得:S［﹁H1，E］=0，S［﹁H2，E］=0;

(2)由析取原理得:S［H1∨﹁H1，E］=I，S［H2∨﹁H2，E］=I;

(3)由賦值規則得:H1∨﹁H1=I，H2∨﹁H2=I;因此(H1∨﹁H1)?(H2∨﹁H2);

(4)由齊一律得:S(H1∨﹁H1，E)=S(H2∨﹁H2，E)=I;

因此(3)和(4)不矛盾。

可見，修正后的否定原理不會導致系統矛盾。同時修正后的否定原理給予了競爭假說一定的地位，但它又不會對被驗假說構成威脅，因為I的支持力低于任一大于零級的支持等級的支持力。從而其推廣應用也更加寬泛，更能貼近科學的實際。比如，基于反射和折射實驗，光的粒子性得到大于零級的支持時，光的波動性不被否定，反之亦然。

第三，修正后的否定原理采取弱否定策略，大大提高了它的辯護功能。科恩系統在對休謨問題的解決上曾遭到這樣的批評:由于歸納概率邏輯系統的局部化程度過高，因此它們的辯護性過低。綜觀科恩系統的全貌，可以看到科恩一方面努力保持著他的系統在正向(歸納支持)上的開放性，一方面又在負向(否定規則)上是完全封閉的。其原因是，科恩在假說提供歸納支持的同時在竭盡全力地對它給予最大程度的保護。因此，他不得不構造復雜的邏輯句法，不斷提高其系統的局部化程度。修正方案對否命題賦值為I，這一策略既打破了科恩系統在負向上的封閉性，同時對假說又不構成威脅。因此，修正方案雖然未觸及科恩的局部支持系統，但它對否定律的弱化使得整個系統更加柔性，從而能大大提高它的辯護功能。

當然，還應看到，盡管對否定原理的技術性修正使得科恩體系在理論上更一致、應用上更恰當，但在整體上它仍然面臨著語境等方面的困境。正如凱伯格所說:“局部歸納法無論在技術上作出怎樣的改進，它都面臨一個一般性的挑戰，即如何判別由最初的不同資料或背景知識所導致的意見分歧;局部歸納法不可能解決這一問題，除非它適當擴展其歸納辯護所依據的語境，但這樣一來它又不可避免地趨向整體辯護和整體歸納。”［2］因此，在局部辯護綱領的指引下，非帕斯卡概率邏輯的研究任重道遠。

［1］Cohen L J.The Probable and the Provable［M］.Loden:Oxford University Press，1977.

［2］何向東.“歸納問題”的邏輯哲學研究述評［J］.哲學研究，2005(12):79 －83.

［3］鞠實兒.非巴斯卡歸納概率邏輯研究［M］.杭州:浙江人民出版社，1993.

［4］張巨青.科學邏輯［M］.2版.長春:吉林人民出版社，1987.

［5］張大松.科學確證的研究進路探微［J］.江海學刊，2009(6):24－29.