改進灰色預測模型在城市用水量預測中的應用

■羅 松，孫傳斌 ■九江市城市規劃市政設計院，江西 九江 332000

城市用水量預測對于城市規劃、供水系統的管理及指導城市供水設施的建設有著重要的意義。隨著我國城市與工業生產的規模不斷擴大，水作為城市生存和發展的制約性因素，在我國大部分城市成為稀缺資源，全國2/3的城市面臨缺水。合理地預測城市用水量，對城市具有顯著的社會意義和經濟意義。目前，常用的城市用水量預測方法有年增長法、GM(1，1)灰色模型法、時間序列法、回歸分析預測法等。

GM(1，1)模型具有要求歷史用水量數據少、不考慮分布規律、不考慮變化趨勢、運算方便、易于檢驗等優點，因此得到了廣泛應用，并取得了令人滿意的效果。但是還存在這一定的局限性:一是當數據離散程度越大，即數據灰度越大，則預測精度越差;二是不太適合給水系統的長期后推若干年的預測［1］。所以，需對預測模型進行一定的改進，使得預測精度(0)(k+1)=(1)(k+1)-(1)(k)高。

Verhulst模型是1837年德國生物學家Verhulst在研究生物繁殖規律時提出的。其基本思想是生物個體數量是呈指數增長的，受周圍環境的限制，增長速度逐漸放慢，最終穩定在一個固定值。Verhulst模型主要用來描述具有飽和狀態的過程，即“S”型過程，常用于人口預測、生物生長、繁殖預測及產品經濟壽命預測等［2］。

1 模型介紹

1．1 GM(1，1)模型

設為x(0)為n個元素的原始數列:

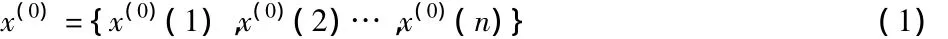
其中，x(0)(k)≥0，k=1，2，…，n;

x(1)為x(0)的一階累加(1-AGO)序列:

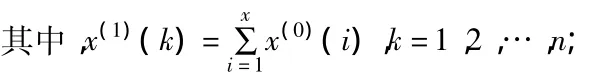
z(1)為x(1)的緊鄰均值生成序列:

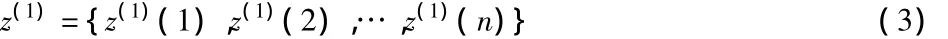
其中，z(1)(k)=0．5x(1)(k)+0．5x(1)(k-1);k=2，3，…，n．

建立灰色GM(1，1)模型的一級白化微分方程為

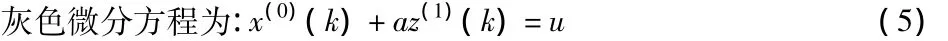
其中，a—為發展系數;u—為灰色作用量。

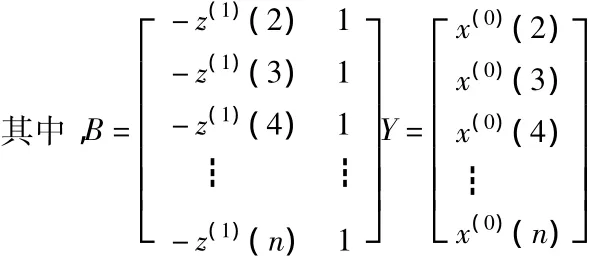
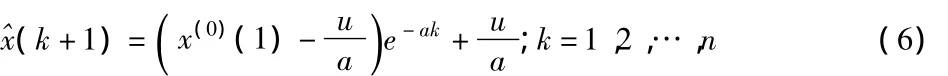
對此式做一階累減(IAGO)還原計算，得原始序列的GM(1，1)預測模型為:

1．2 新陳代謝GM(1，1)模型

隨著觀測時間的推移，不斷有新的觀測信息加入原始序列中，使得數據信息量不斷豐富。由于數據值不斷增長，早起數據所占份額逐漸減少而顯得較為次要，于是提出有了新陳代謝模型，也就是在增加一個新信息的同時，把最早的一個老信息刪掉，從而維持數據總量保持不變［3］。

新陳代謝處理后x(0)得:

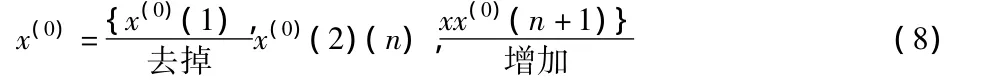
接下來重復GM(1，1)模型(2)～(7)進行建模計算

1．3 灰色Verhulst模型

根據原始數據序列x(0)分別得到一次累加新數據序列x(1)以及緊鄰均值生成序列z(1)，建立灰色Verhulst模型的白化微分方程為:

a、b 含義同 GM(1，1)模型，a——發展系數，b——灰作用量。

灰色Verhulst模型的時間響應式:

其中，k=1，2，…，n-1

的Verhulst預測模型還原值為:

當 k→∞時，若a＞0，則x(1)(k)→0;若a＜0，則x(1)(k)→，即有充分大的k使x(1)(k+1)和x(1)(k)充分接近，此時x(0)(k+1)=x(1)(k+1)x(1)(k)≈0，系統趨近死亡，在處理“S”型或部分“S”型過程時預測精度更高。

2 模型精度檢驗實例分析

一般認為，預測精度≥85%，則認為預測是成功的［3］。目前預測值精度分級的一般原則如表1所示，表中MAPE為平均絕對百分比誤差，其計算公式如下:

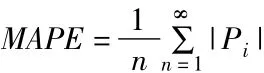
式中:n—樣本數據個數;Pi—相對百分比誤差(%)。

表1 預測精度劃分表

表2 陜西省某城鎮水廠2010年的供水量(單位:m3)

對該城鎮1月～9月用水量進行建模，預測10月～12月用水量。

從表3可以得出，GM(1，1)模型、新陳代謝GM(1，1)模型以及灰色Verhulst模型的MAPE分別是6.16%、5.32%、6.07%，都屬于高精度預測。預測效果:新陳代謝GM(1，1)模型＞灰色Verhulst模型＞GM(1，1)模型。

表3 用水量預測值與實際值的比較結果

3 結論

本文采用灰色系統理論對城市用水量進行預測，針對GM(1，1)模型存在的問題，提出了新陳代謝GM(1，1)模型。結果表明，新陳代謝模型(動態等維新息模型)比基本的GM(1，1)模型和Verhulst模型預測精度更高，擬合效果更好，適用于城市的用水量預測。

［1］尹學康，韓德鴻.城市需水量預測［M］.中國建筑工業出版社，2006(2):111.

［2］郭廣猛.用 GM(1，1)模型和Verhulst模型進行建筑物沉降預測［J］.巖土工程界，2000，3(10):33-37.

［3］趙鴻賓.給水管網系統理論與分析［M］.中國建筑工業出版社，2003.