正整數方冪方陣的循序逐增規律與費馬定理——兼證費馬定理不成立的必要條件

張爾光

（韶關市人大機關，廣東 韶關512000）

筆者研究結果表明，任何一個正整數方冪（n＞1）均可表為數學方陣。正整數方冪方陣的各種數的循序逐增現象，反映了正整數方冪方陣的循序逐增規律性，而費馬定理與此規律有著密切聯系。

1 正整數2次冪方陣的循序逐增規律

筆者認為，要想弄清楚正整數方冪方陣的循序逐增規律性，應從對正整數2次冪方陣的研究入手，弄清楚正整數方冪方陣與正整數方冪的三角矩陣之間的關系，注重對正整數方冪方陣的各種數的循序逐增現象的研究，進而發現矩陣的各種數的循序逐增規律。

1.1 任何一個正整數平方均可表為由“1”組成的方陣或三角矩陣

筆者在《地圖與數學的組合、排列及三角矩陣》一文（見《數學學習與研究》2011年第19期）中，經證明得出結論：任何一個正整數（n＞1）的2次冪均可表為一個由“1”組成的方陣，而且這個方陣既可表為一個由“1”組成的三角矩陣，也可表為兩個由“1”組成的三角矩陣。

根據正整數2次冪的方陣和三角矩陣的規律，遵循組合數“循序逐增”的基本原理，正整數的2次冪的方陣和三角矩陣可以圖1來表示。其定理為

圖1 n2的方陣和三角矩陣圖

從“n2的方陣和三角矩陣圖”看出，正整數2次冪的方陣，其方陣元素“1”是曲尺形排列，雖與三角矩陣的表達方式不同，但兩者表達的意思（或叫內容）相同。可見，正整數方冪方陣與正整數方冪三角矩陣是等同關系。據此，為著論證的方便，筆者在下文論證正整數方冪方陣時，則以三角矩陣的表達方式來替代，并用之于證明方陣的各種數的循序逐增的規律。

1.2 方陣（三角矩陣）的各種數的概念

圖2 三角矩陣（方陣）的各種數的概念解釋圖

本文所說的方陣（三角矩陣）的各種數，是指矩陣的邊線數、中線數、同行數列相加之和（見圖2圖解）。所說的各種數的循序逐增現象，是指這些數及數列差反映出來的規律有序的東西。

從圖2看出，邊線數，是指三角矩陣的左斜邊線數和右斜邊線數，左斜邊線數即是方陣的第一列數，右斜邊線數即是方陣的第一行數；中線數，是指位于三角矩陣中間的數，即是方陣的左上角至右下角的斜線數；同行數列相加之和，是指三角矩陣同一行的數列各數相加后的得數，即是方陣的曲尺形行列數各數相加后的得數。

規律1 正整數2次冪方陣的同行數列相加之和是循序逐增的兩個正整數平方差的依次排列。

從圖1看出，正整數2次冪方陣（三角矩陣），其同行數列相加之和是循著奇數“1,3,5,7,9,…”的次序排列。這“1,3，5,7，9,…”，既是奇數，又是與正整數的2次冪有著密切聯系的數：1是12-02之差，3是22-12之差，5是32-22之差，7是42-32之差，9是52-42之差，此后依次類推。可見，正整數2次冪方陣，其同行數列相加之和為循序逐增的兩個正整數的平方差（即“n2-(n-1)2”之差）的依次排列，亦是循序逐增的兩個正整數的同次方差（即“nk-(n-1)k”之差）的依次排列。這表明正整數方冪方陣是一個循序逐增的擴展過程。此規律是正整數方冪方陣的核心規律。

規律2 正整數2次冪方陣的同行數列相加之和的數列差是循序逐增的兩組“兩個正整數平方差”之差。

從“n2的方陣和三角矩陣圖”的同行數列相加之和可知，正整數2次冪方陣的同行數列相加之和的數列差依次為“2,2,2,…”。此數列差“2”，是不同的前后兩組“兩個正整數平方差”之間的差。正整數方冪方陣的“同行數列相加之和的數列差”的公式為：

同行數列相加之和的數列差=[(n+1)k-nk]-[nk-(n-1)k]

如：1與3之差為2，已知1是“12-02”之差，3是“22-12”之差。據此，n為1，k為2，那么，得:[(1+1)2-12]-[12-(1-1)2]=(22-12)-(12-02)=3-1=2

再如：3與5之差為2，已知3是“22-12”之差，5是“32-22”之差。據此，n為2，k為2，那么，得:[(2+1)2-22]-[22-(2-1)2]=(32-22)-(22-12)=5-3=2

又如：5與7之差為2，已知5是“32-22”之差，7是“42-32”之差。據此，n為3，k為2，那么，得:[(3+1)2-32]-[32-(3-1)2]=（42-32）-（32-22）=7-5=2

2 正整數方冪方陣的各種數的循序逐增規律

筆者研究結果表明，遵循正整數方冪方陣的循序逐增規律，任何一個正整數方冪均可表為其同行數列相加之和為循序逐增的兩個正整數的同次方差的方陣。

現以正整數的3次冪、4次冪、5次冪的方陣為例予以證明。例證1 正整數3次冪的方陣（三角矩陣）,見圖3。

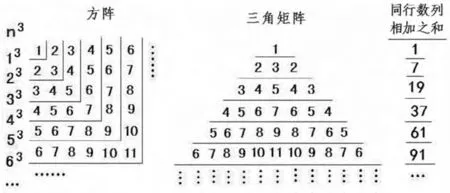
圖3 正整數3次冪的方陣和三角矩陣

例證2 正整數4次冪的方陣（以三角矩陣表達），見圖4。

圖4 正整數4次冪方陣（以三角矩陣表達）

例證3 正整數的5次冪的方陣（以三角矩陣表達）,見圖5。

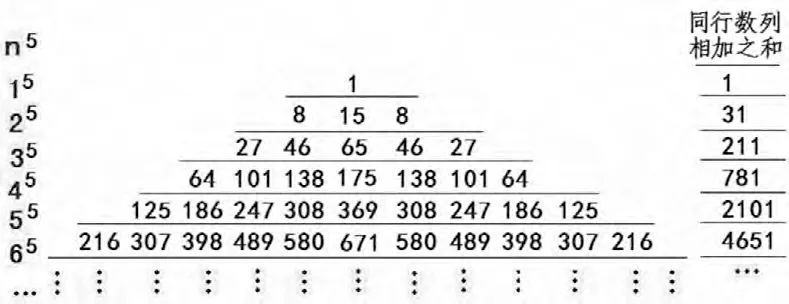
圖5 正整數5次冪方陣（以三角矩陣表達）

2.1 正整數方冪方陣的同行數列相加之和及數列差的循序逐增規律

現依照正整數方冪方陣的循序逐增原理，對正整數的3次冪、4次冪、5次冪的方陣（三角矩陣）的各種數及數列進行分析。

從圖3看出，正整數3次冪方陣，k=3，其同行數列相加之和依次為“1,7,19,37,61，…”，是前后兩個正整數的同次方差（即“n3-(n-1)3”之差）的依次排列。“n3-(n-1)3”可表為“nk-(n-1)k”。

從圖4看出，正整數4次冪方陣，k=4，其同行數列相加之和依次為“1,15,65,175,369，…”，是前后兩個正整數的同次方差（即“n4-(n-1)4”之差）的依次排列。“n4-(n-1)4”可表為“nk-(n-1)k”。

從圖5看出，正整數5次冪方陣，k=5，其同行數列相加之和依次為“1,31,211,781，2101，…”，是前后兩個正整數的同次方差（即“n5-(n-1)5”之差）的依次排列。“n5-(n-1)5”可表為“nk-(n-1)k”。

依照歸納法，得出結論，正整數方冪方陣的同行數列相加之和為前后兩個正整數的同次方差的依次排列。前后兩個正整數的同次方差可表為“nk-(n-1)k”。

根據正整數方冪方陣的同行數列相加之和的循序逐增規律，可求得正整數方冪方陣的各行同行數列相加之和累加得數的循序逐增規律，也即是正整數方冪方陣的循序逐增規律。見圖6。

根據圖6反映出來的方陣的同行數列相加之和循序累加的規律，求得正整數方冪（方陣）的定理，即：

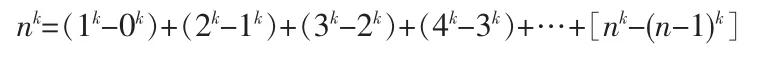
圖6

根據方陣的同行數列相加之和循序累加的規律，可知：

根據正整數方冪方陣的同行數列相加之和數列，可求得正整數方冪方陣的同行數列相加之和數列差之定理為：

同行數列相加之和數列差=［(n＋1)k－nk］-［nk-(n-1)k］

2.2 正整數方冪方陣的中線數及數列差的循序逐增規律

從圖3看出，正整數3次冪方陣，k=3，其中線數數列依次為“1,3，5,7,9，…”，是前后兩個正整數的“n3-1-(n-1)3-1”之差的依次排列。“n3-1-(n-1)3-1”可表為“nk-1-(n-1)k-1”。

從圖4看出，正整數4次冪方陣，k=4，其中線數數列依次為“1,7,19,37,61，…”，是前后兩個正整數的“n4-1-(n-1)4-1”之差的依次排列。“n4-1-(n-1)4-1”可表為“nk-1-(n-1)k-1”。

從圖5看出，正整數5次冪方陣，k=5，其中線數數列為“1,15,65,175,369,…”前后兩個正整數的“n5-1-(n-1)5-1”之差的依次排列.“n5-1-(n-1)5-1”可表為“nk-1-(n-1)k-1”。

依照歸納法，得出結論，正整數方冪方陣的中線數的循序逐增規律是前后兩個正整數的“nk-1-(n-1)k-1”之差的依次排列。

根據正整數方冪方陣的中線數的循序逐增規律，可求得正整數方冪方陣的中線數數列差之定理為：［(n＋1)k-1－nk-1］-［nk-1-(n-1)k-1］

2.3 正整數方冪方陣的邊線數及數列差的循序逐增規律

從圖3看出，正整數3次冪數方陣的邊線數數列是“1,2,3,4,5，…”（即“13-2,23-2,33-2,43-2,53-2…”）的依次排列。 “13-2,23-2,33-2,43-2,53-2…”可表為“1k-2,2k-2,3k-2,4k-2,5k-2…”。

從圖4看出，正整數4次冪數方陣的邊線數數列是“12，22，32，42，52，…”(即“14-2,24-2,34-2,44-2,54-2…”)的依次排列。“14-2,24-2,34-2,44-2,54-2…”可表為“1k-2,2k-2,3k-2,4k-2,5k-2…”。

從圖5看出，正整數5次冪數方陣的邊線數數列是“13，23，33，43，53，…”(即“15-2,25-2,35-2,45-2,55-2…”)的依次排列。 “15-2,25-2,35-2,45-2,55-2…”可表為“1k-2,2k-2,3k-2,4k-2,5k-2…”。

依照歸納法，得出結論，正整數方冪方陣的邊線數的循序逐增規律為“1k-2,2k-2,3k-2,4k-2,5k-2…”的依次排列。

已知正整數方冪方陣的邊線數數列為“1k-2,2k-2,3k-2,4k-2,5k-2…”的依次排列，那么，可知邊線數數列差的循序逐增規律，即：

第一行邊線數與第二行邊線數之差為“2k-2-1k-2”之差；

第二行邊線數與第三行邊線數之差為“3k-2-2k-2”之差；

第三行邊線數與第四行邊線數之差為“4k-2-3k-2”之差；

第四行邊線數與第五行邊線數之差為“5k-2-4k-2”之差；

第五行邊線數與第六行邊線數之差為“6k-2-5k-2”之差，此后依次類推。

2.4 正整數方冪方陣的同行邊線數至中線數的數列差的循序逐增規律

根據正整數方冪方陣的中線數的循序逐增規律和邊線數的循序逐增規律，可知:

第一行邊線數與第二行邊線數之差是為第二行邊線數至中線數的數列差，即“2k-2-1k-2”之差；

第二行邊線數與第三行邊線數之差是為第三行邊線數至中線數的數列差，即“3k-2-2k-2”；

第三行邊線數與第四行邊線數之差是為第四行邊線數至中線數的數列差，即“4k-2-3k-2”；

第四行邊線數與第五行邊線數之差是為第五行邊線數至中線數的數列差，即“5k-2-4k-2”。此后依次類推。2.5 正整數方冪方陣的規律模式

根據上文求得的正整數方冪方陣的各種數的循序逐增規律之定理，可構建組成正整數方冪方陣的規律模式，見圖7、圖8。

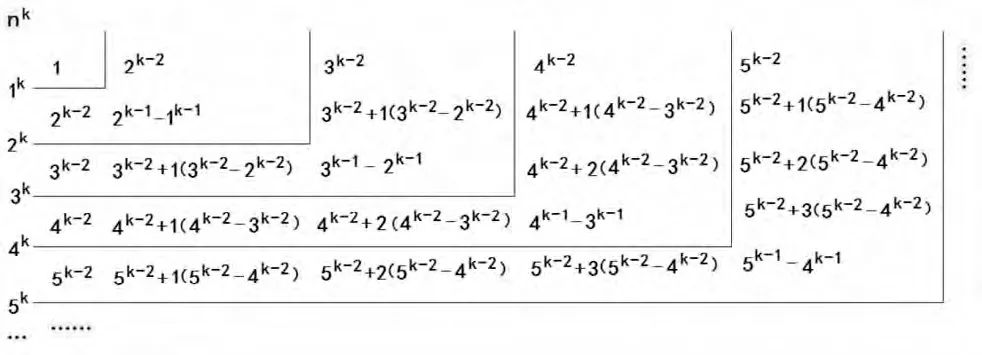
圖7 （正整數方冪方陣的規律模式之一）

圖8 （正整數方冪方陣的規律模式之二）

那么，依照正整數方冪方陣的規律模式可構建出正整數任何次冪（正整數n＞1，次冪k＞1）的方陣。對此，筆者無需舉例贅證。

3 正整數的“xn+yn=zn”方程式與正整數方冪矩陣

正整數的“xn+yn=zn”方程式中的一種數學現象：

在正整數的“xn+yn=zn”方程式中，如將xn、yn、zn三者的次數由1至2、至3的等式做分析，不難發現其存在的一種數學現象。

事實告訴我們，當xn、yn、zn三者的次數為1（即n=1）時，即在“x+y=z（z≥2）”方程式中，任何一個z（即大于1的正整數）均可表為兩個正整數相加之和，反之，任何兩個正整數相加之和均可表為另一個正整數。因此，“x+y=z（z≥2）”成立。

事實還告訴我們，xn、yn、zn三者的次數為2時，即在“x2+y2=z2（z≥2）”方程式中，不可能做到任何一個大于1的正整數平方（即z2）均可表為兩個正整數平方相加之和，比如62、72、82不可能表為一個正整數平方加另一個正整數平方；反之，也不可能做到任何一個正整數平方加一個正整數平方等于另一個正整數平方（即z2），比如“22+32”、“32+52”、“45+52”，其和不可能等于另一個正整數平方。因此，在“x2+y2=z2（z≥2）”方程式中，只是存在部分一個正整數平方（即z2）可表為兩個正整數平方相加之和，部分一個正整數平方加一個正整數平方等于另一個正整數平方（即z2）。所以，正整數的“x2+y2=z2（z≥2）”方程式有成立與不成立之分。

事實和費馬定理告訴我們，xn、yn、zn三者的次數為3時，即在“x3+y3=z3（z≥2）”方程式中，任何一個正整數三次方（即z3）均不可能表為兩個正整數三次方相加之和，反之，任何兩個正整數三次方相加不可能等于另一個正整數三次方（即z3）。因此，正整數的“x3+y3=z3（z≥2）”不成立

可見，在正整數的“xn+yn=zn”方程式中，冪的次數僅是從1至2、至3的增升，其結果就發生了“完全成立→部分成立→完全不成立”如此截然不同的質的變化。正整數的“xn+yn=zn”方程式中反映出來的冪的次數循序逐增現象，有它的不可理解性。顯然，如從正整數的“x2+y2=z2”的成立等式和不成立等式的異同之處入手，運用方陣等式的方法來研究它，這對于另辟蹊徑破解費馬定理是有積極意義的。

4 正整數的“x2+y2=z2”中成立等式與不成立等式的異同

筆者研究結果表明，在成立的正整數的“x2+y2=z2”的方陣等式中又分為兩類，一類是z2方陣的“末行數列相加之和”等于x2的方陣等式；另一類是x2、y2、z23個方陣是為方陣群的方陣等式，其3個方陣群是前一類方陣等式的3個方陣分別乘上“n2”而組成。

4.1 z2方陣的“末行數列相加之和”等于x2的方陣等式的證明

根據正整數的“x2+y2=z2”的方程式可知，z2方陣＞x2方陣、y2方陣。筆者依照從小到大的次序，設定x2方陣＜y2方陣＜z2方陣。那么，在z2方陣的“末行數列相加之和”等于x2的方陣等式中，x2、y2、z23個方陣之間存在什么內在聯系呢？為此，請看圖9。

為著證明的表述不發生混淆，方陣的“同行數列相加之和”的行次以“z”表示。

從圖9看出，當方陣的z行的“同行數列相加之和”為奇數平方時，必定會產生一個成立的“x2+y2=z2”的方陣等式。

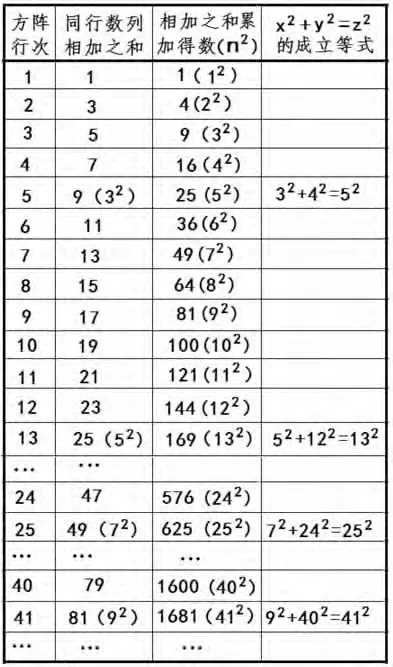
圖9

如，方陣第5行“同行數列相加之和”9為32，就產生了“32+42=52”的成立等式，即z2為52，y2為42，x2為32；

再如，方陣第13行“同行數列相加之和”25為52，就產生了“52+122=132”的成立等式，即z2為132，y2為122，x2為52；

又如，方陣第25行“同行數列相加之和”49為72，就產生了“72+242=252”的成立等式，即z2為252，y2為242，x2為72。

從圖9中成立的“x2+y2=z2”的方陣等式看出，y2方陣就是z2方陣減去末行數列而形成的方陣，x2方陣的x2等于z2方陣的“末行數列相加之和”。據此，可以說，y2方陣和x2方陣是z2方陣分解出來的兩個完整的方陣。為此，現對z2方陣做分解證明。

為便于區別，將z2方陣的末行元素以“①”來表示。

例證1 “52=42+32”方陣等式的z2方陣的分解證明

已知 z2方陣為52方陣，z2=52。

第一步 將52方陣的末行數列分解出去，則為y2方陣，即方陣等式中的42方陣。可見，(5-1)2=42，表為(z-1)2=y2。

第二步 將52方陣分解出來的末行數列組成x2方陣，即方陣等式中的32方陣。可見，52-(5-1)2=32，表為z2-(z-1)2=x2。z2方陣的“末行數列相加之和”等于x2。

第三步 將z2方陣及分解形成的y2方陣和x2方陣表為方陣等式：

從上方陣等式看出，52方陣=42方陣+32方陣。可見，“52=42+32”的方陣等式成立。此證。

例證2 “132=122+52”方陣等式的z2方陣的分解證明

已知 z2方陣為132方陣，z2=132。

第一步 將132方陣的末行數列分解出去，則為y2方陣，即方陣等式中的122方陣。可見，(13-1)2=122，表為(z-1)2=y2。

第二步 將132方陣分解出來的末行數列組成x2方陣，即方陣等式中的52方陣。可見，132-(13-1)2=52，表為z2-(z-1)2=x2。z2方陣的“末行數列相加之和”等于x2。

第三步 將z2方陣及分解形成的y2方陣和x2方陣表為方陣等式：

從上方陣等式看出，132方陣=122方陣+52方陣。可見，“132=122+52”的方陣等式成立。此證。

例證3 “252=242+72”方陣等式的z2方陣的分解證明

已知 z2方陣為252方陣（方陣元素以點表示1），z2=252。

第一步 將252方陣的末行數列分解出去，則為y2方陣，即方陣等式中的242方陣。可見，(25-1)2=242，表為y2=(z-1)2。

第二步 將z2方陣分解出來的末行數列組成x2方陣，即方陣等式中的72方陣，可見，252-(25-1)2=72，表為z2-(z-1)2=x2。z2方陣的“末行數列相加之和”等于x2。

第三步 將z2方陣及分解形成的y2方陣和x2方陣表為方陣等式：

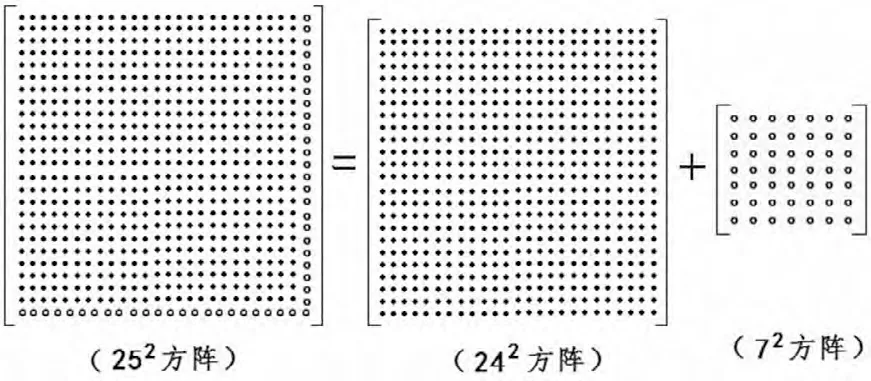
從上方陣等式看出，252方陣=242方陣+72方陣。可見，“252=242+72”的方陣等式成立。此證。

綜上例證1、例證2、例證3的證明，依照歸納法，可知z2方陣的“末行數列相加之和”等于x2的方陣等式中的x2、y2、z23個方陣之間的關系：

結論1 y2方陣是z2方陣減去末行數列后形成的方陣，可表為(z-1)2=y2。

結論2 x2方陣是由z2方陣的末行數列組成的方陣，z2方陣的“末行數列相加之和”等于x2，可表為z2-(z-1)2=x2。

結論3 z2方陣可分解為2個小于其的完整的方陣，即為y2方陣和x2方陣，可表為z2=y2+x2=(z-1)2+［z2-(z-1)2］。4.2 x2、y2、z23個方陣是為方陣群的方陣等式

例證1 “62+82=102”的方陣等式

從“62+82=102”的方陣等式可知，x2方陣為62方陣，而62=(32*22)，表明62方陣是由“22”個32方陣組成的方陣群；y2方陣為82方陣，而82=(42*22)，表明y2方陣是由“22”個42方陣組成的方陣群；z2方陣102方陣，而102=(52*22)，表明z2方陣是由“22”個52方陣組成的方陣群。由此可知，“62+82=102”的方陣等式的3個方陣，是“32+42=52”的方陣等式的3個方陣分別乘上“22”而組成的方陣群,即“62+82=102”等于“(32*22)+(42*22)=(52*22)”。又從102方陣可知，其末兩行的“同行數列相加之和”相加（即17+19）之和為36，而36=62，正是“102-82”（即“z2-y2”）之差。可見，z2-y2=x2。“62+82=102”的方陣等式成立。

例證2 “92+122=152”的方陣等式

從“92+122=152”的方陣等式可知，x2方陣為92方陣，而92=(32*32)，表明92方陣是由“32”個32方陣組成的方陣群；y2方陣為122方陣。而122=(42*32)，表明y2方陣是由“32”個42方陣組成的方陣群；z2方陣為152方陣，而152=(52*32)，表明z2方陣是由“32”個52方陣組成的方陣群。由此可知，“92+122=152”的方陣等式的3個方陣，是“32+42=52”的方陣等式的3個方陣分別乘上“32”而組成的方陣群,即“92+122=152”等于“(32*32)+(42*32)=(52*32)”。又從152方陣可知，其末三行的“同行數列相加之和”相加（即25+27+29）之和為“81”，而“81”=92，正是“152-122”（即“z2-y2”）之差，可見，z2-y2=x2。“92+122=152”的方陣等式成立。

綜上例證1、例證2的證明，x2、y2、z23個方陣為方陣群的方陣等式的特征可歸納為：

特征1 z2、y2、x2此3個方陣群是z2方陣的“末行數列相加之和”等于x2的方陣等式的3個方陣分別乘上“n2”而組成。

特征2 z2方陣減去y2方陣（即“z2-y2”）之差，是正整數平方,等于x2方陣的x2，可表為x2=z2-y2。

4.3 兩類正整數的“x2+y2=z2”中成立等式的關系及共同特征

從上證明可知，z2方陣的“末行數列相加之和”等同于x2的方陣等式，與x2、y2、z23個方陣為方陣群的方陣等式具有源與流的關系。后者的z2、y2、x23個方陣為前者的z2、y2、x23個方陣分別乘上“n2”而組成的方陣群。據此，在已知前者的3個方陣的條件下，同時乘上“n2”，可知后者的z2、y2、x23個方陣群，求得后者的“x2+y2=z2”的成立等式。見圖10。

從圖10看出，z2方陣的“末行數列相加之和”等于x2的方陣等式存在，那么，x2、y2、z2為方陣群的方陣等式必定存在。可見，前者衍生后者，后者延伸前者，兩者是源與流的關系，是一脈相承的同一本質的方陣等式。正因為如此，所以，在兩者的“x2+y2=z2”的方陣等式中，不論是x2=z2-y2，還是y2=z2-x2都是成立的。而這，正是兩類正整數的“x2+y2=z2”的成立等式的共同特征。

圖10

遵循正整數方冪方陣的循序逐增規律，根據“x2+y2=z2”方陣等式中x2、y2、z23個方陣之間的關系，可設定，z2方陣是存在的已知方陣，y2方陣也是存在的已知方陣（即為“(z-1)2方陣”），而未知的則是x2方陣，即z2方陣的“末行數列相加之和”（即“z2-(z-1)2”之差）是否等于x2。基于這一解讀，在求證正整數的“x2+y2=z2”的等式時，只需求證z2方陣的“末行數列相加之和”是否等于x2這個關鍵點便見分曉，而無需作更多的證明。

4.4 正整數的“x2+y2=z2”不成立等式的根本原因

例證1 62=52+x2等式的z2方陣的分解證明

已知 z2方陣為62方陣（見圖11），62方陣減去末行數列而形成的y2方陣為52方陣(即(6-1)2=52)；需求證的是62方陣的“末行數列相加之和”（即“62-(6-1)2”）是否等于x2。

圖11

從62方陣可知，其“末行數列相加之和”為62-(6-1)2=11≈3.1662，不是正整數平方。而由62方陣的末行數列(元素)組成的x2方陣（見圖12），處于32余2、42缺5之狀態，是不完整的正整數2次冪方陣。可見，62方陣分解的兩個方陣，y2方陣為52方陣成立，而x2方陣是不完整的方陣。所以，62=52+x2等式作為正整數的“x2+y2=z2”等式是不成立的等式。此證。

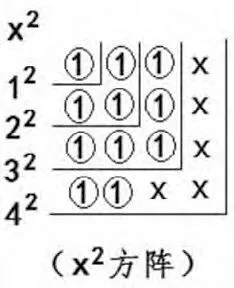
圖12

例證2 72=62+x2等式的z2方陣的分解證明

已知 z2方陣為72方陣（見圖13），72方陣減去末行數列而形成的y2方陣為62方陣（即“(7-1)2=62”），需求證的是72方陣的“末行數列相加之和”（即“72-(7-1)2”之差）是否等于x2。

圖13

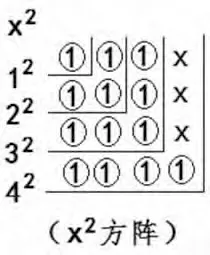
圖14

從72方陣可知，其“末行數列相加之和”為72-(7-1)2=13≈3.60562，不是正整數平方。而由62方陣的末行數列(元素)組成的x2方陣（見圖14），處于32余4、42缺3之狀態，是不完整的正整數2次冪方陣。可見，72方陣分解的兩個方陣，y2方陣為62方陣成立，而x2方陣是不完整的方陣。所以，72=62+x2等式作為正整數的“x2+y2=z2”等式是不成立的等式。此證。

綜合例證1、例證2的證明，得出結論:正整數的“x2+y2=z2”不成立等式的根本原因,在于z2方陣的“末行數列相加之和”（即“z2-(z-1)2”之差）不可表為正整數的平方，z2方陣只能分解為一個完整的y2方陣和一個不完整的x2方陣。

4.5 正整數的“x2+y2=z2”的成立等式與不成立等式的區別

從以上的方陣等式證明可知，正整數的“x2+y2=z2”的成立等式與不成立等式的區別主要在于z2方陣的“末行數列相加之和”（即“z2-(z-1)2”之差）是否等于x2，成立的等式，z2-(z-1)2=x2（包括x2、y2、z2分別乘上“n2”后的“x2=z2-y2”），x2的x是正整數；不成立的等式，則z2-(z-1)2≠x2（包括x2、y2、z2分別乘上“n2”后的“x2≠z2-y2”），x2的x不是正整數。這種區別，還反映在方陣的“同行數列相加之和”與“相加之和累加得數”的兩種數字之關系的不同。成立的等式，因z2方陣的“同行數列相加之和”的平方根是正整數，所以，在“相加之和累加得數”中存在其等同數；不成立的等式，因z2方陣的“同行數列相加之和”的平方根不是正整數，所以，在“相加之和累加得數”中不存在其等同數。

4.6 結論

綜上正整數的“x2+y2=z2”的方陣等式的證明，得出結論：

結論1 在正整數的“x2+y2=z2”的方陣等式中，z2方陣是方陣等式的核心方陣，是設定的已知方陣。可通過已知的z2方陣，推知y2方陣的y2=(z-1)2，x2方陣的x2=z2-(z-1)2。

結論2 z2方陣的“末行數列相加之和”（即z2-(z-1)2）是組成x2方陣的元素，是方陣等式的關鍵要素。

結論3 “x2=z2-(z-1)2”的x為正整數是方陣等式成立的必要條件，是求證方陣等式是否成立的關鍵點。

5 對費馬定理的證明

1995年英國數學家安德魯·懷爾斯與其學生理查·泰勒應用橢圓曲線的原理對費馬定理做出了證明。筆者認為，費馬定理是一個關于正整數方冪之間關系的方程式命題，應用正整數方冪方陣的原理對其做出證明，這似乎更合乎該命題的題意。基于這個觀點，筆者嘗試運用方陣等式的證明方法，從費馬定理不成立的必要條件的角度，對費馬定理進行論證。

5.1 費馬定理的另一種表述

四川科學技術出版社于1985年出版的《古今數學趣話》一書的《能下金蛋的母雞——“費馬猜測”古今談》對費馬定理的原本內容是這樣表述的：“不可能把一個整數的立方表為兩個整數的立方和，也不可能把一個整數的四次冪表為兩個整數的四次冪和。一般來說，不可能把任意一個次數大于2的整數的方冪，表為兩個整數的同次方冪之和。”用現代的專業用語來說，就是當n＞2時，不定方程：

xn+yn=zn不存在正整數解。

筆者認為，上段文字關于費馬定理的內容，用正整數方冪方陣的原理的語言來表述，則為：

不可能把一個整數的立方的方陣表為兩個整數的立方的方陣，也不可能把一個整數的四次冪的方陣表為兩個整數的四次冪的方陣。一般來說，不可能把任意一個次數大于2的整數的方冪的方陣，表為兩個整數的同次方冪之方陣。其不定方陣等式為

xn方陣+yn方陣=zn方陣 n＞2時不存在正整數解。

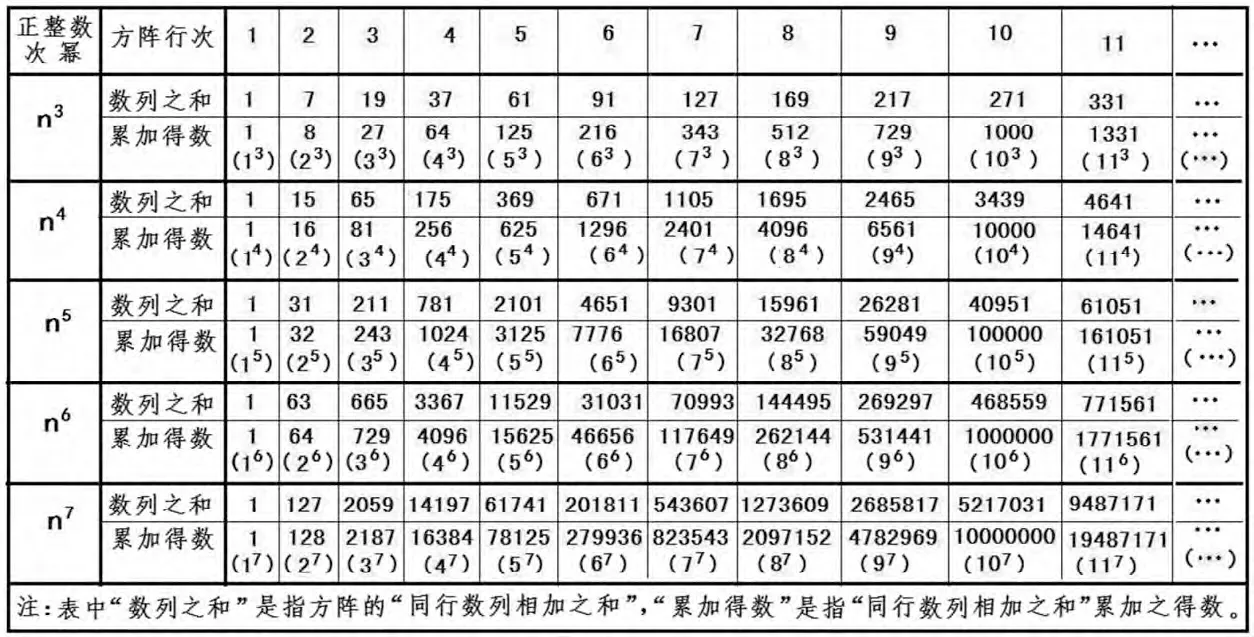
圖15

5.2 對“xn+yn≠zn”（n≥3）的證明

根據對正整數的“x2+y2=z2”的方陣等式的證明結論，遵循正整數方冪方陣的循序逐增原理，在正整數次冪n＞2的“xn+yn=zn”的方陣等式中，同樣zn方陣是設定的已知方陣，yn方陣為zn方陣減去末行數列而形成的方陣﹝即yn=(z-1)n﹞，是可推知的方陣，而xn方陣的“xn=zn-(z-1)n”x為正整數是方陣等式成立的必要條件，zn方陣的“末行數列相加之和”是否等于xn，是求證方陣等式是否成立的關鍵點。對此，既可從方陣的“同行數列相加之和”的數字中有無與“相加之和累加得數”等同的數予以驗證，也可直接對“xn=zn-(z-1)n”做出證明。

5.2.1 方陣的“同行數列相加之和”中無與“相加之和累加得數”等同的數

事實證明，在正整數次冪n＞2后，方陣的“同行數列相加之和”中（“1”除外，下同）不存在有與“相加之和累加得數”等同的數。請看圖15。

圖15是正整數1至11、次冪為3至7的方陣的“同行數列相加之和”和“相加之和累加得數”的統計表。從該表看出，在正整數的3次冪、4次冪、5次冪、6次冪、7次冪的方陣的兩種數字中，2至11行的“同行數列相加之和”中均不存在有與“累加得數”等同的數。據此，得出結論：在正整數次冪n＞2后，方陣的“同行數列相加之和”的數字中（1除外）不存在有與“相加之和累加得數”等同的數。

5.2.2 對“xn=zn-(z-1)n”的“x”是不是正整數的證明

筆者研究結果表明，在正整數次冪n＞2后，之所以方陣的“同行數列相加之和”中不存在有與“相加之和累加得數”等同的數，這是因為，“xn=zn-(z-1)n”等式中的“x”不是正整數。

例證1 以正整數的3次冪方陣的“同行數列相加之和”為例

綜上實例證明，得出結論，在“x3=z3-(z-1)3”等式中，在z為正整數的條件下，“x”不是正整數，即“z3=y3+x3”不存在正整數解。此證。

例證2 以正整數4次冪方陣的“同行數列相加之和”為例

綜上實例證明，得出結論，在“x4=z4-(z-1)4”等式中，在z為正整數的條件下，“x”不是正整數，即“z4=y4+x4”不存在正整數解。此證。

例證3 以正整數5次冪方陣的“同行數列相加之和”為例

綜上實例證明，得出結論，在“x5=z5-(z-1)5”等式中，在z為正整數的條件下，“x”不是正整數，即“z5=y5+x5”不存在正整數解，此證。

依照歸納法，得出結論：在“xn=zn-(z-1)n”等式中，在z為正整數的條件下，“x”不是正整數。因此，“zn=yn+xn”不存在正整數解。所以，費馬定理成立。此證。

5.2.3 對“xn=zn-(z-1)n”等式是否成立的證明

在z、x均為正整數的條件下，“xn=zn-(z-1)n”等式是否成立呢?現予以證明。

設定“z2=y2+x2”是成立的正整數2次冪的方陣等式。據此，次冪n＞2時，依照正整數方冪方陣的原理，“zn=yn+xn”可表為：

z2*zn-2=(y2*yn-2)+(x2*xn-2)

正整數方冪方陣的循序逐增原理告訴我們，在正整數次冪n＞2時，不論正整數z及方冪如何升增，“z2*zn-2=zn”都是成立的。而作為zn方陣減去末行數列而形成的yn方陣，不論zn方陣的z及n如何升增，其“yn=(z-1)2*(z-1)n-2”（即“(z-1)n=(z-1)2*(z-1)n-2）”）都是成立的。(如，設zn=53，已知z=5，n=3，那么，yn=(z-1)2*(z-1)n-2=(5-1)2*(5-1)3-2=42*4=43;又如，設zn=67，已 知z=6，n=7，那 么，yn=(z-1)2*(z-1)n-2=(6-1)2*(6-1)7-2=52*55=57。)

那么，當zn方陣的n＞2時，其“zn-(z-1)n=xn”是否成立呢。對此，將該等式分為“zn-(z-1)n”（zn方陣的“末行數列相加之和”）和“xn”（即xn方陣的xn）兩部分來解讀，q并做出證明。

依照zn方陣的zn=z2*zn-2的表達方式，zn方陣的末行數列相加之和“zn-(z-1)n”則可表為：（z2*zn-2）-[(z-1)2*(z-1)n-2]

例證1 設z2=y2+x2為52=42+32，現求證zn方陣為53方陣時，“zn-(z-1)n=xn”是否成立。

已知 z=5，n=3。那么，將“z=5，n=3”套入“（z2*zn-2）-[(z-1)2*(z-1)n-2]”得:

可見,53-43≠33，zn-(z-1)n≠xn。所以，“zn-(z-1)n=xn”不成立。此證。

例證2 設z2=y2+x2為132=122+52，現求證zn方陣為135方陣時，“zn-(z-1)n=xn”是否成立。

已知z=13，n=5。那么，將“z=13，n=5”套入“（z2*zn-2）-[(z-1)2*(z-1)n-2]”得:(132*135-2)-[(13-1)2*(13-1)5-2]=135-125=371293-248832=122461可見,135-125≠55，zn-(z-1)n≠xn。所以，“zn-(z-1)n=xn”不成立。此證。例證3 設z2=y2+x2為252=242+72，現求證zn方陣為254方陣時，“zn-(z-1)n=xn”是否成立。

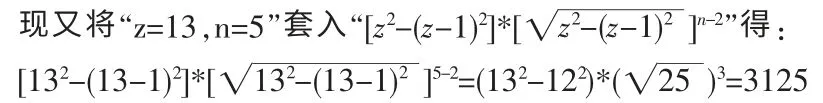
已知z=25，n=4。那么，將“z=25，n=4”套入“（z2*zn-2）-[(z-1)2*(z-1)n-2]”得:

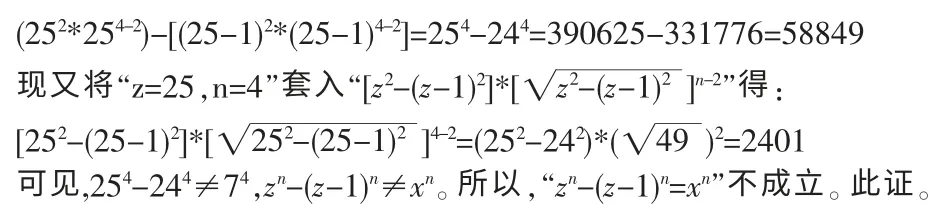
綜例證1、例證2、例證3的證明，依照歸納法，得出結論：當正整數次冪n＞2時，因為zn-(z-1)n≠xn，所以，“zn-(z-1)n=xn”不成立。當正整數次冪n＞2時，因為“zn-(z-1)n=xn”不成立，所以，“zn=yn+xn”也不成立。此證。

5.3 總的證明結論

事實上，根據“xn方陣+yn方陣=zn方陣”成立等式的必要條件和費馬定理給出的“同次方冪”的原則，用逆向思維方式去思考，不難明白，對費馬定理的證明，其實就是對“（x2*xn-2）+（y2*yn-2）≠z2*zn-2”做出證明。現證明如下：

同 理，∵zn-2＞yn-2，∴（y2*yn-2）÷zn-2＜y2，亦 即（y2*yn-2）＜（y2*zn-2），或 是（y2*yn-2）≠（y2*zn-2）。

由此得出結論：（x2*xn-2）+（y2*yn-2）≠z2*zn-2。所以，費馬定理成立。此證。

［1］張爾光.正整數的方冪的方陣與費馬定理——費馬定理不成立的必要條件[J].數學學習與研究,2012,23:115-119.