基于MATLAB的6自由度機器人假肢工作空間分析

朱雪梅，姚有峰，汪明珠

（皖西學院基礎實驗中心傳感網與信息處理綜合應用創新平臺，安徽 六安237012）

隨著我國經濟的發展，社會保障制度在逐漸得到完善，針對殘疾人士的基本型輔助器具的研發也受到了重視，可替代人手的機器人假肢研究變得更加重要［1］。機器人學的研究一般在機械結構設計之初要進行機器人運動學分析，機器人運動學方程的建立是為了對所設計的結構進行數學分析，方便對機器人運動軌跡進行計算機仿真、機器人控制方程的設計以及機器人結構和運動設計的計算［2］（P3-4），從而實現對機器人假肢的控制，增強控制系統穩定性，調高抗干擾能力［3］。解決機器人假肢運動學方程的主要方法有數值法和解析法，其中數值法計算方法簡單，但計算速度慢，不能獲得全部的解。解析法能得到所有可能的解，但是計算過程復雜。將數值法的蒙特卡洛法和計算機仿真軟件MATLAB相結合，可以很好地解決機器人運動學方程解的問題。

1 建立假肢數學模型

機器人假肢主要是需要通過對機械結構的控制實現人體上下肢的基本功能，在對機器人假肢進行設計之初，要充分考慮設計所需實現的功能，根據各個桿件的結構以及自由度的數量設計出合理的假肢結構圖。在機器人假肢結構圖的基礎上，根據各個關節參數建立其D-H坐標系，從而得到假肢運動學方程［4-6］，建立機器人假肢的數學模型。對于機器人假肢控制系統的設計，則主要是在結構圖及運動學方程的基礎上對各個自由度及關節實現控制。

1．1 機器人假肢結構圖

根據仿人形上肢的機器人上假肢的功能需求，充分考慮各個關節桿件的結構參數設計了6自由度上假肢圖件，如圖1所示，基礎底部即肩部，又稱作0桿，通過0桿將假肢與人體固定；肩部旋轉構件稱作1桿，通過該桿件實現人大臂的旋轉功能；大臂構件稱作2桿，即實現人的大臂支撐功能；小臂轉動支撐稱作3桿，即實現人的小臂支撐功能；小臂轉動構件稱作4桿，即實現人的小臂轉動功能；假手構件稱作5桿，即實現人的手部功能。該機器人上假肢包括6個自由度，其中5個是運動自由度，1個是手部局部自由度。根據其結構與動作特性，其各種參考如圖1所列，其中a圖是正視圖，b圖是側視圖。

1．2 建立D-H坐標系

6自由度機器人假肢運動學主要研究機器人假肢的運動，包括上假肢的各個手部桿件機構姿態以及各個關節運動角度等運動的學科［7］（P98-100），在已知機器人假肢的所有連桿長度和關節角度等的基礎上，計算出機械結構末端手部的位姿［8］（P49-50）。如果想要實現假肢手部末端抓取物體的功能，即控制手部末端到期望的位置，并且實現抓取及其他相關動作，則必須知道假肢的連桿長度和各個關節所需轉動的角度，這就叫做逆運動學分析［9］。由此可見，正運動學方程解的結果是唯一的，而逆運動學方程具有多解性，這就給假肢姿態問題的求解帶來很大的困難［10］。首先要根據機器人假肢結構圖建立D-H坐標系（圖2）。

圖1 機器人假肢結構圖

機器人假肢的運動學坐標系如圖2所示，以大地坐標系為基礎坐標系，則機器人假肢的固定基坐標x、y、z構成的絕對坐標系，原點位置設在基座與桿件的交點上，即大臂與手臂的支撐桿件的交點處。而坐標x0、y0、z0構成的坐標系o0以及坐標x1、y1、z1構成的坐標系o1的原點也是在此交點處，這樣建立固定基的便利之處是可以減少支撐處到大臂長度d0的影響；由坐標x2、y2、z2構成的坐標系o2與小臂連桿相連，坐標z1和坐標z2的距離是a2；由坐標x3、y3、z3構成的坐標系o3與坐標x2、y2、z2構成的坐標系o2在一個原點，可以減少小臂抬起的過程中位移的影響；由坐標x4、y4、z4構成的坐標系o4與手部相連，小臂長為d4；由坐標x5、y5、z5構成的坐標系o5的位置與手部工作中心點重合，其坐標系是由手部的運動方式來確定的，坐標系o4與坐標系o5之間的距離為a5。在建立坐標系時，一定要注意第一個和最后一個坐標系的原點的位置，它們將決定機器人的總變換方程。

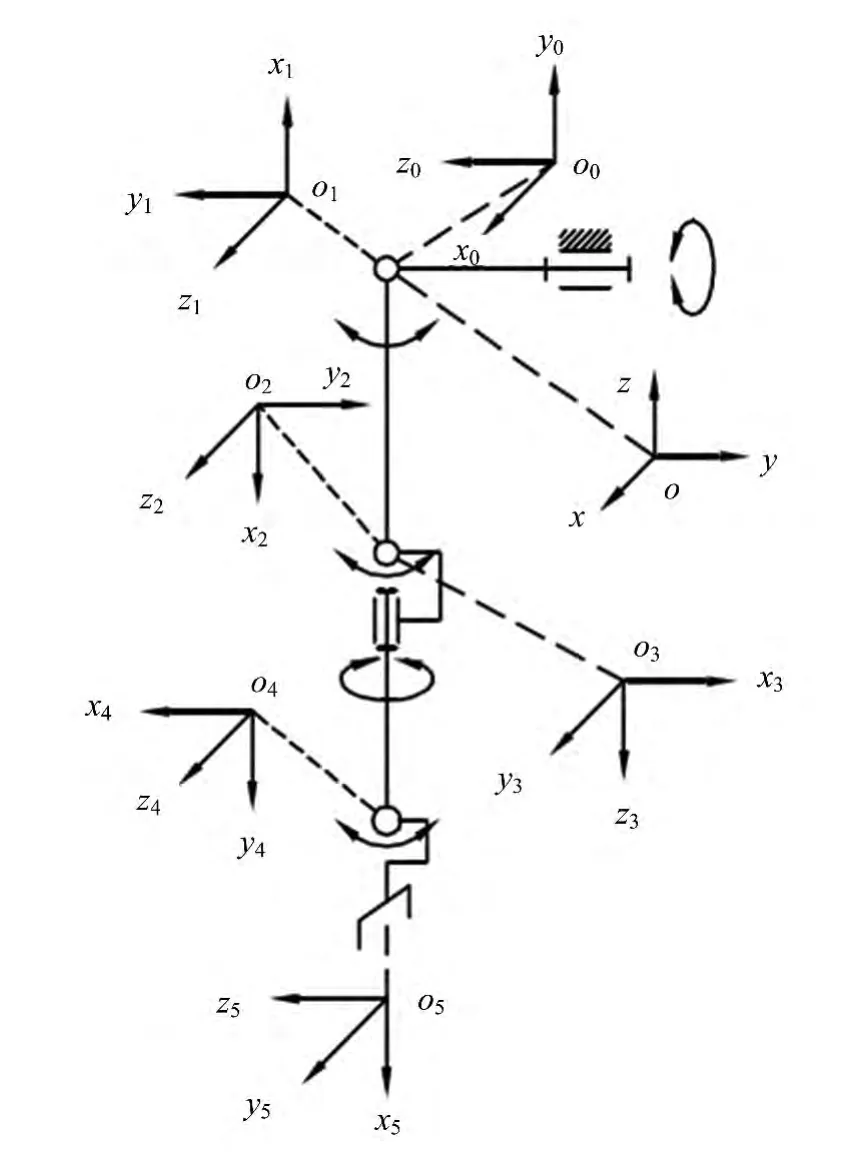
圖2 機器人假肢的D-H坐標圖

1．3 機器人假肢的運動學方程

結合圖2“D-H法”建立的坐標系圖，可以推導出機器人假肢的運動學方程，具體方法如下：首先根據坐標圖確定各個關節的參考坐標系，然后確定各個關節連接桿件相對于所選擇的基礎坐標系的空間幾何關系，即關節坐標系之間的變換，最后計算出機器人上假肢手部末端坐標系和基礎坐標系之間的變換矩陣，得到整個機器人上假肢的運動學方程。其中，根據變換矩陣的需要，表明坐標間關系的四個參數為［8］（P11）：

ai：是從zi-1軸和zi軸間的最小距離；

αi：是由zi-1軸轉向zi軸繞xi軸的偏轉的關節角度（按右手規則）；

θi：是由xi-1軸轉向xi軸繞zi-1軸的偏轉的關節角度（按右手規則）；

di：是從第i-1坐標系的原點到zi-1軸和xi軸的交點沿zi-1軸的距離。

由前面的原則可得，通過D-H法建立6自由度機械手臂運動學坐標系參數，如表1所示。

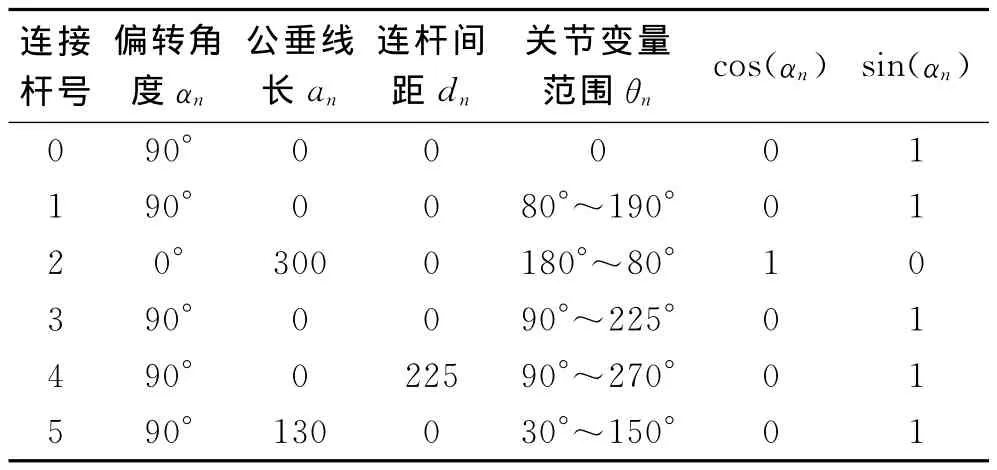
表1 機器人假肢連桿與關節參數

根據表1所示的參數得到A矩陣，并用A矩陣來表示T矩陣。機器人假肢的手部末端裝置即為連桿6的坐標系，它與連桿i-1坐標系的關系可由i-1T6表示為［4］（P53）：

其中：

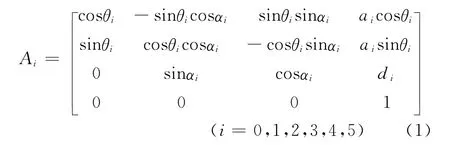
根據式（1）可以列出其各桿件的A矩陣并將表（1）數據代入該矩陣可得：

用公式iT6＝AiAi＋1…A5類推：

于是，可求得機器人假肢的T變換矩陣

2 機器人假肢工作空間的確定

機器人假肢的工作空間就是機器人假肢正常受控制執行動作時，手部末端構件坐標系的原點所能達到位置點的集合，是由整個上假肢自身的關節桿件長度和旋轉角度等特性指標決定的。對于機器人假肢，其機械結構、連桿長度、各個關節的坐標系以及運動學方程都是已知的，則機器人假肢末端的手部能到達的點的集合就稱為機器人假肢的工作空間，可以通過數學方程結合機器人的連桿和關節的約束條件，求出每個關節的運動范圍。

2．1 機器人假肢的工作空間分析

機器人假肢有6個自由度，其工作空間的形成可以看做是各個自由度相對上個自由度旋轉運動所形成的空間，具體過程：手部末端執行器的坐標系o5繞桿件4坐標系o4的z4軸旋轉到的坐標位置，這些坐標點在坐標系o4中形成的空間W4（p）；然后W4（p）隨桿件4的坐標系o4一起繞桿件3坐標系o3的z3軸旋轉，則在坐標系o3中形成了工作空間W3（p）。同樣的，在坐標系o2、o1、o0分別旋轉后可以形成假肢各個關節桿件對應的工作空間。由于各個關節的旋轉角度和桿件參數的限制，在機器人假肢各個關節自由度運動時可能會出現手部末端桿件不能達到的坐標點，這些坐標位置點在工作空間之內形成的空間稱為空腔，而穿透工作空間的坐標點形成的空間則稱為空洞。

將機器人假肢運動學方程結合表1的桿件參數和關節可變化的范圍，解出手部末端機構坐標系原點的全部解，表1中連接桿件的長度參數是確定的，則手部末端機構的工作空間則主要是由各個關節角度變化量θi（i＝1，2，3，4）決定的，用齊次坐標表示為：

2．2 機器人假肢的工作空間仿真

圖3 機器人假肢工作空間的蒙特卡洛分布圖

將隨機選取的關節變量值θi代入步驟（1）建立的機器人假肢運動學方程數學模型，即可得到假肢手部末端機構在工作空間的任意可到達的點。（4）利用MATLAB仿真軟件的繪圖工具將這些點繪制成圖形顯示出來，即機器人假肢手部末端機構工作空間的蒙特卡洛分布圖。

可任意設置計算的循環次數并繪圖，選取的計算次數越多，則計算所得到的末端隨機點越多，但也增加了計算的數據量和仿真的時間，因此選擇合適的計算次數即可。綜合考慮選擇把計算循環次數設為5 000，對應地可以得到假肢末端手部對應的5 000個隨機點，分析結果如圖3所示。

從程序仿真運行結果可以看到，機器人假肢末端手部機構的工作空間為一近似缺橢球的形狀，基本實現人類手臂在大臂固定時手部能到達的空間范圍點。且該空間范圍內部空間緊湊，無空穴和空洞，蒙特卡洛法可以把機器人假肢的工作空間用圖形直觀顯示出來，不僅可以直觀地看到所設計的假肢的理想效果，精確了軌跡規劃，而且有利于后續的控制系統的設計等工作。

3 結語

針對仿人形上肢機器人假肢的基本功能需求，提出了一種基于6自由度機器人上假肢運動學和工作空間分析方法。根據所設計的假肢結構圖數學模型，建立D-H坐標系，并結合各個關節參數和角度變化進行運動學方程的建立和工作空間的求解。借助蒙特卡洛方法，通過MATLAB進行機器人假肢的工作空間的仿真分析。此方法不僅精確了機器人假肢軌跡規劃，而且對機器人假肢的設計具有實用價值。

［1］肖源．我國殘疾人輔助器具技術發展現狀及其原因的剖析［J］．科技創新導報，2011，3（28）：246-246．

［2］黃真，孔令富，方躍法．并聯機器人機構學理論及控制［M］．北京：機械工業出版社，1997．

［3］田西勇．機器人軌跡規劃方法研究［D］．北京：北京郵電大學（碩士學位論文），2008．

［4］蔡自興．機器人學［M］．北京：清華大學出版社，2000．

［5］A．Green，J．Z．Sasiadek．Adaptive Control of a Flexible Robot Using Fuzzy Logic［J］．Journal of Guidance and Dynamics，2005，28（1）：36-42．

［6］孟慶鑫，王曉東．機器人技術基礎［M］．哈爾濱：哈爾濱工業大學出版社，2010．

［7］（美）克來格（Craig，J．J．）．機器人學導論［M］．贠超，譯．北京：機械工業出版社，2006．

［8］（美）尼庫（Niku，S．B．）．機器人學導論——分析、系統及應用［M］．孫富春，譯．北京：電子工業出版社，2004．

［9］王海，蔡英鳳，張為公．一種7DOF機械臂逆運動學解析算法及應用［J］．江蘇大學學報，2011（5）：254-259．

［10］熊大柱．一種7自由度生機電假肢手臂的結構設計及運動學分析［D］．武漢：華中科技大學（碩士學位論文），2013．