動態隨機非參數數據包絡分析法及其應用

汪茂泰，何永芳

（1.安徽工程大學 人文學院，安徽 蕪湖 241000；2.西南財經大學 工商管理學院，成都 611130）

隨機非參數數據包絡分析（StoNED）是Kuosmanen（2006）提出的一種效率測度的非參數前沿分析方法。該方法較好的將隨機誤差項與非效率項進行了有效分離，又免除了生產函數形式預設導致設定誤差與效率估計相混淆的缺陷；且該方法僅依賴于DEA和SFA所建立的原有概念和原理，無需引入新的概念和工具，對于熟悉DEA和SFA的學者可以比較容易理解和掌握。因此，StoNED一經提出就得到廣泛的應用和擴展。

1 動態隨機非參數數據包絡分析法

StoNED標準模型最早圍繞截面數據開展研究，但需要對技術非效率項以及隨機誤差項做標準的SFA假設（非效率項和隨機誤差項必須分別服從截取正態分布和標準正態分布）。而面板數據有助于減少截面數據模型的參數分布的相關假設，并且可以采用純非參數形式來估計前沿面以及非效率項。

考慮到生產技術和效率變化，我們在生產函數 f(x)的基礎上引入時間變量t，把生產函數重新設定為f(x ，t)，t=0，1，···，T ；同時用 ui(t)替代非效率項ui。

在StoNED標準模型中，假設合成誤差的方差是獨立于廠商規模的，一旦違背此假設可能會導致不同廠商之間出現異方差性。因此，我們采用乘法誤差結構形式來從降低可能存在的異方差性。基于應用方便的目的，我們將StoNED模型設定為如下形式：

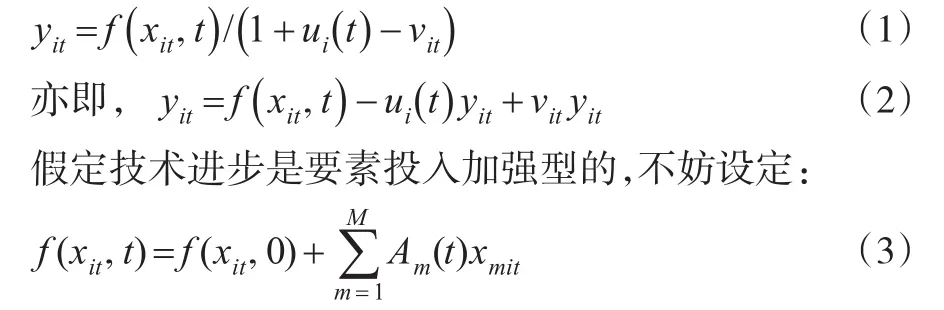
其中，f(xit，0)是指基期的生產函數，而函數Am(t)表示投入型技術進步。可以證明：若 f(xit，0)單調遞增且Am(t)≥0 ，則 f(xit，t)也是單調遞增的；若 f(xit，0)是凹的，則 f(xit，t)也是凹的。顯然，方程（3）優良的特性給我們在StoNED框架下設置技術進步提供了方便：可以用非參數形式來估計基期生產函數 f(xit，0)，用非參數或者參數形式來設置技術進步。更重要的是，不管如何設置Am(t)的形式，都不會影響 f(xit，t)的凹性在不同時期的一致性。

為了減少待估參數的個數，我們采用二次方程（新引入2M個未知參數）設定技術進步：

在CNLS（凹面非參數最小二乘法）框架中，使用純非參數形式來設定效率變化是不可行的，除非強加眾多的嚴格假設。如果沒有足夠的嚴格約束，效率變化很難與隨機誤差區別開。因此，我們采用半參數方法：非參數形式估計生產函數，參數方程來估計非效率項ui(t)。按照Cornwell et a（l1990）的做法，將非效率項設定為二次多項式：

若bi=ci=0，表示效率變化水平是常數；若bi?0，ci=0，表示效率變化呈線性增長；若ci≠0，表示效率呈非線性變化。

將式（2）、（3）、（4）和式（5）相結合，得到待估計的回歸方程：

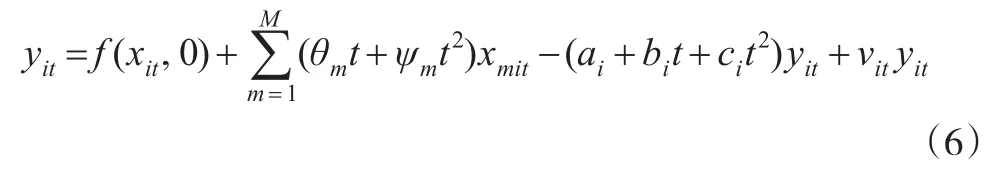
為了估計基期生產函數 f(xit，0)以及參數θ、ψ、a、b、c，構建CNLS估計模型：

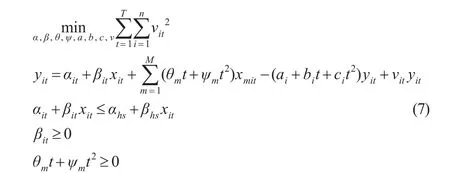
其中，目標函數是最小化誤差項的L2范數。第一約束是回歸方程，用切超平面αit+βitxit來表示基期生產函數f(xit，0)；第二約束是用不等式對切超平面施加凹形限定；第三約束是對生產函數施加單調性限制；第四約束是技術限制。以上約束條件可以確保 f(xit，t)的單調性和凹性。

以上模型可以采用GMAS（General Algebraic Modeling System）軟件進行估計。

2 數據來源與處理

本文所使用的原始數據來自中國官方公開出版的2004～2010年間服務業分行業數據。經過適當處理，這些數據構成了一個包括14個服務行業在7年里共98個觀察值的面板數據。

2.1 分行業的實際產出

本文采用增加值作為度量服務業產出的指標。2004～2010年服務業分行業的增加值數據來自歷年的《中國第三產業統計年鑒》和《中國統計年鑒》。《中國統計年鑒》給出了歷年第三產業增加值指數（上年為基期）。由于數據的限制，除了“交通運輸、倉儲和郵政業”、“批發和零售業”、“住宿和餐飲業”、“金融業”以及“房地產業”直接使用各自給定的增加值指數外，其他行業均統一使用“其他”欄給定的增加值指數。將上述增加值指數換算成以2004年為基期的增加值平減指數，并對歷年服務業各行業名義增加值進行折實處理，就可以得到歷年服務業分行業的實際產出。

2.2 分行業的勞動投入

勞動投入雖然包括就業人數、勞動收入、勞動時間、勞動強度以及勞動質量等方面的內容，但眾多學者均認為用就業人數來代替勞動投入的變動是合適的（原毅軍等，2009），因此本文也采用此指標來衡量勞動投入。

《中國第三產業統計年鑒》并未公布2004年以來分行業年底就業總人數，只公布了城鎮單位、私營和個體就業人數等城鎮就業人數。考慮到安徽的就業結構比較接近于全國的水平，所以我們假設全國第三產業各行業鄉村就業人員比例結構與安徽是一致的，從而可以根據第三產業總就業人數、城鎮就業人數以及安徽省第三產業各行業鄉村就業人員結構估計出全國第三產業各行業鄉村就業人數，再將城鎮就業人數與鄉村就業人數相加就近似得到2004～2010年分行業年底就業總人數。

2.3 分行業的資本投入

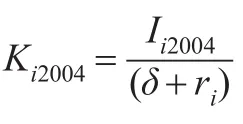
《中國統計年鑒》、《中國第三產業統計年鑒》和《固定資產投資統計年鑒》給出了全行業固定資產投資指數，但未給出分行業固定資產投資指數。我們假設各行業的固定資產投資指數均等于全行業的固定資產投資指數，并調整為以2004年為基期，由此得到各行業實際固定資產投資值。結合上述估算辦法，就可以得到歷年各行業資本存量實際值。

3 模型及其測算

結合模型（7），本文的動態隨機非參數數據包絡分析模型設定為：

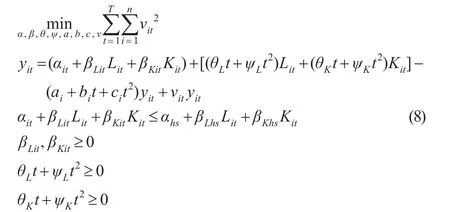
運用GAMS軟件，可以估計出相應的參數值。

關于技術進步Am(t)，結果顯示資本增強型技術進步幾乎為零（θK=0，ψK=0），技術進步主要體現在勞動投入上（θL=-0.064，ψL=0.064）。據測算，在7年時間里，技術進步生產函數增長了1.7倍。近年來，服務業從業人員的數量穩步上升，從業人員的質量快速提高，大量優質人才的加入使得服務業的技術進步明顯。

將 f(xit，0)與Am(t)相結合來考察要素投入的邊際產出（βmit+tθm+t2ψm），結果如表1所示。2004～2010年，各行業的勞動邊際產出出現明顯增長，而資本的邊際產出出現下降或者維持不變。近年來，我國服務業的資本和勞動投入都顯著增加，但相對于勞動投入，資本投入的增加更加明顯（各行業固定資產投資實際年增長率在14%以上）。因此，從邊際報酬遞減規律來看，出現邊際產出變化的分異也是一個可以預期的結果。從估計值來看，房地產行業的勞動邊際產出遠遠高于其他行業，而居民服務和其他服務業相對最低；各行業資本的邊際產出非常低，幾乎接近于零。按照西方經濟學理論，在完全競爭市場中，太低的邊際產出意味著投資過度，而較高的邊際產出意味著投資不足。雖然我國服務業市場化進程在加快，但還未形成完全競爭狀態，在部分行業還存在嚴格的政府管制。因此，我們不能用西方經濟學理論來解釋這一現象。我們認為，我國資本投資并不過度，在政府管制下，有限的資本投資并沒得到充分的利用，存在大量的資本浪費和閑置，太低的邊際產出原因在于資本的質量以及利用不足。

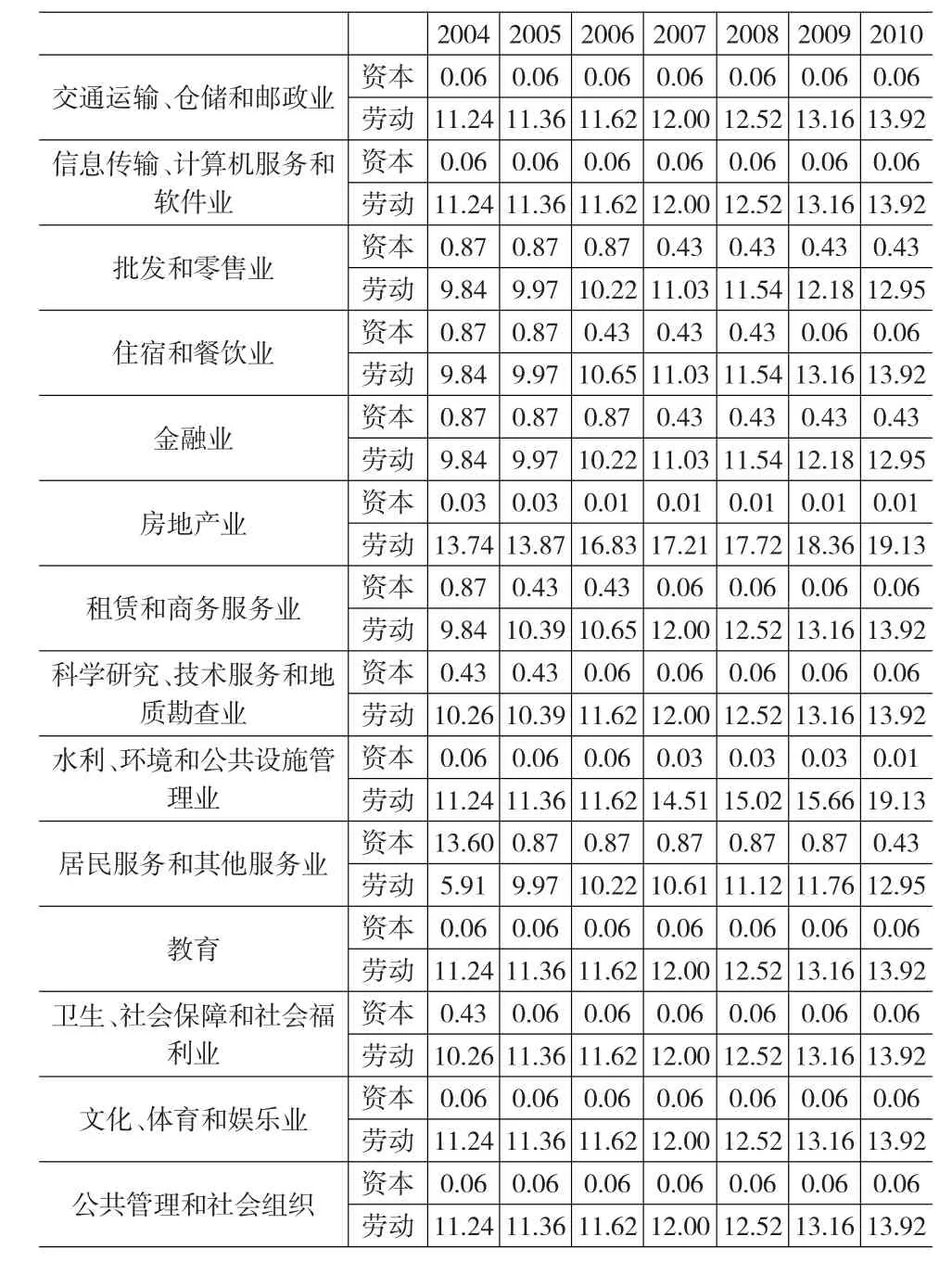
表1 投入的邊際產出的估計值

為清晰的比較不同年份不同行業的效率水平，我們采用標準化的形式[1/(1+ui(t))]來表示效率值，結果如表2所示。所有效率估計值均落在區間[0，1]上，效率估計值1代表最有效率，0代表最沒效率。注意，這里效率估計值是全效率估計值，既包括技術效率又包括規模效率等。由表2可見：在2004～2010年間，金融業都是最有效率的；其次是房地產業，但其效率值呈逐年下降趨勢；信息傳輸、計算機服務和軟件業以及交通運輸、倉儲及郵政業的效率也相對較高，并且逐年穩步上升。最沒效率的行業為文化、體育和娛樂業，但近年來其效率得到顯著提升。為剔除行業自身內外部環境對效率估計的影響，我們考察了不同行業年平均效率變化率（相對效率可以很好的捕捉截面的異質性）。如表2所示：居民服務和其他服務業、批發和零售業以及租賃和商務服務業顯示出相對較高的效率改善（年均6%以上）；而住宿和餐飲業以及教育業效率改善比較溫和（年均在1%左右）。整體來看，雖然我國服務業效率較低，但大部分行業均進入了快速上升階段，只有房地產業以及水利、環境和公共設施管理業等出現效率下降現象。這也反映出我國服務業發展的階段特征：長期以來，我國服務業進入管制較嚴、市場壟斷程度較高，一定程度上制約了技術進步。隨著服務業市場化程度的逐步提高，為應對外部競爭的加劇，各行業內部更加注重組織結構的調整和優化完善，這就為效率提升提供了巨大空間。

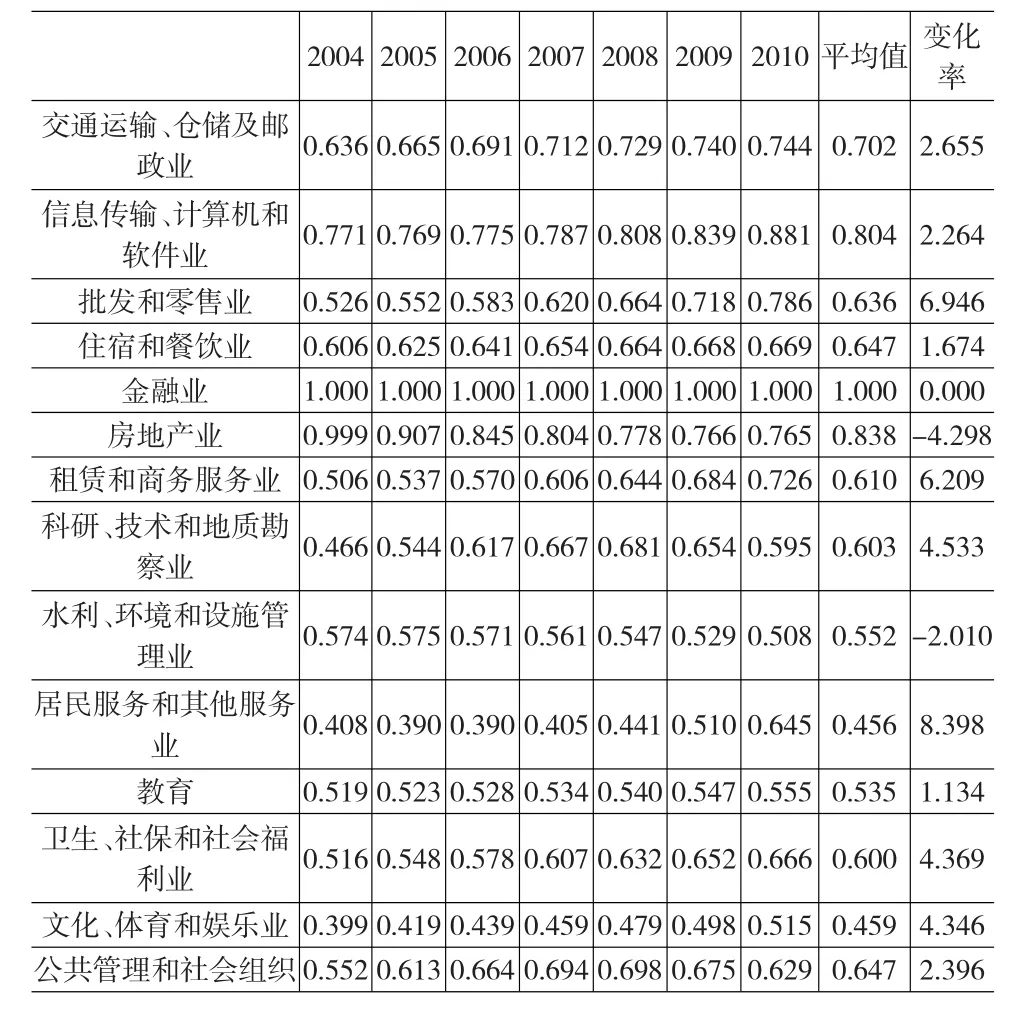
表2 2004～2010年相對效率水平值[1/(1+ui(t))]及其變化率 (%)

4 結論

為解釋跨期生產技術和效率變化，我們介紹了動態隨機非參數數據包絡分析方法。

隨后運用動態隨機非參數數據包絡分析方法，對我國服務業各行業的技術進步及其效率改善進行了測算。2004～2010年，我國服務業資本增強型技術進步幾乎為零，技術進步主要體現在勞動投入上。整體來看，我國服務業效率水平較低，但大部分行業均進入了快速上升階段。

動態隨機非參數數據包絡分析法為考察跨期技術變化和效率變化提供了很好的度量工具，但我們也應注意到：隨機非參數數據包絡分析法雖然綜合了DEA和SFA的優良特質，但也保留了它們的部分局限性。在模型的設定中，眾多的約束條件也帶來了這種分析方法的局限性。另外，在考察技術進步時，時間跨度要足夠長。本文受制于數據的可得性，我們只采用了7年的數據，技術進步的測算結果就不太準確。

[1]Kohli U.A Cross-National Product Function and The Derived Dem and for Imports and Supply of Exports[J].Canadian Journal of Economics,1982,(18).

[2]Kuosmanen T.Stochastic Nonparametric Envelopment of Data:Combining Virtue of SFA and DEA in A Unified Framework[C].MTT Discussion Paper,2006.

[3]Kuosmanen T.Stochastic Nonparametric Envelopment of Panel Data:Frontier Estimation With Fixed and Random Effects Approaches[C].MTT Discussion Paper,2010.

[4]籍艷麗,趙麗琴.一種效率測度的新方法：隨機非參數數據包絡分析法[J].統計與決策，2011,（5）.

[5]原毅軍,劉浩,白楠.中國生產性服務業全要素生產率測度——基于非參數Malmquist指數方法的研究[J].中國軟科學,2009,(1).