基于單整相依測度的非線性協整檢驗方法

周麗莉，李 露，丁東洋

（南昌大學a.廉政研究中心；b.經濟管理學院，南昌330031）

0 引言

在對多元間序列變量建模時，首先需要進行變量的非平穩性檢驗與變量間的協整關系檢驗。如果兩個或多個非平穩時間序列變量的線性組合是平穩的，則表明它們之間存在線性協整關系。根據Granger的定義，存在變量yt，xt～I(1)滿足如下回歸模型：

其中α稱為r×n調節矩陣，β是n×r協整向量矩陣，εt～N(0，Σ)，r和 p分別表示協整秩和滯后期長度，式（2）反映了時間序列變量對非均衡偏差進行修正的動態機制。基于式（1）和式（2）表述的標準協整理論，大量的研究對其進行完善和拓展，線性協整理論日趨成熟。

研究表明，宏觀和金融時間序列中存在大量的非線性特征，如貨幣供給沖擊對產出的非對稱性效應；通貨膨脹與通貨緊縮的非線性轉換調節特征；資本市場具有分形和非線性特征；以及收入差距與經濟增長的非線性協整關系等等[1]。雖然線性協整模型在數據分析中仍占有重要地位，但是在上述問題中卻無法有效地描述變量之間的非線性和非對稱變動特征。為了將非線性模型引入時間序列分析，大量的研究開始對線性協整進行拓展，隨著Tong(1990)[2]構建閾值自回歸模型以及Balke and Fomby(1997)[3]提出兩變量的閾值協整模型，非線性時間序列分析領域逐漸成為研究熱點。至今，非線性時間序列研究取得了豐碩的成果，但是對于非平穩序列的非線性協整理論研究在國內外都處于起步階段，面臨的問題很多，采用的方法也有所差異。現有的文獻中主要具有兩種途徑將格蘭杰定理拓展到非線性協整分析，一種是基于格蘭杰的表述定理構建非線性誤差修正模型，其基本思路與格蘭杰表述定理并無根本差異，關鍵在于描述非線性特征；第二種則是直接進行非線性協整關系分析，涉及的問題主要包括非線性協整關系的表述，非線性協整關系的檢驗以及非線性協整模型的推斷等。本文針對非線性協整分析的第二種途徑，基于單整相依測度建立檢驗框架，重點探討同時處理非平穩性和非線性的統計方法，并指出未來的研究方向。

1 非線性協整關系的表述

1.1 線性協整的非線性拓展

Granger(1995)[4]首先提出使用長期記憶和短期記憶的概念，如果時間序列的信息隨著時間而衰減，那么稱為短期記憶的，否則稱為長期記憶的，對長記憶時間序列的沖擊有永久性影響。如果存在函數 f使得zt=f(yt，xt)具有短期記憶特征，則稱長期記憶序列yt和xt之間是非線性協整關系。將I(0)和I(1)的線性概念正確拓展后，可將協整的含義從線性拓展到非線性。給定條件均值函數E(yt+h|It)，It=(xt，xt-1，...)表示處于時間 t的已知信息。對于任意時間 t，隨 h 逐漸增大時，M(t，h)=E(yt+h|It)， h＞0趨于常數μ，則稱序列{yt}是依均值短期記憶的(SMM)。更準確的說，對于所有t，E |M(t，h)-μ|2＜c(h)，當 h趨于無窮時，其中c(h)≡c(h，t)是趨于0的正序。如果{yt}不滿足上述條件，則稱為依均值拓展記憶的(EMM)。從數學上的嚴格性來說，應該指定{yt}是相對于{xt}來說SMM或EMM的，Granger則假定xt=yt，并在后期研究中使用依均值長期記憶(LMM)代替了以往使用的EMM。

然而非平穩序列的非線性轉換無法保證時間的原始性質不發生改變，所以這種直接在線性協整的基礎上拓展的非線性協整定義可操作性差，特別是當時間序列是非線性或非高斯時，無法應用傳統的自相關和周期圖等相依測度方法，原有的檢驗和推斷方法都將失效。而且以上對于非線性協整關系的陳述過于籠統，還可能引發出現識別問題。一些研究認為應該限定函數 f的類型以避免識別問題[5]，一個可行的解決方法是對函數zt=g(yt)-h(xt)變形，再使用條件均值的持續性測度方法。

1.2 基于單整相依測度的非線性協整關系表述

對于任意時間t，隨h逐漸增大時，m(t，h)=E(yt+h|xt)，h＞0趨于常數μ，則稱序列{yt}是配對依均值短期記憶的(PSMM）。更準確的說，對于所有t，E |m(t，h)-μ |2＜c(h)，當h趨于無窮時，其中c(h)≡c(h，t)是趨于0的正序。如果{yt}不滿足上述條件，則稱為配對依均值拓展記憶的(Pair wise EMM,PEMM)。從上述定義和迭代期望定理，可知SMM進程即是PSMM。但反過來說并不成立，存在屬于PSMM但不是SMM的進程，雖然在實際中很少遇到[6]。

當存在非線性（或非高斯分布）時，自協方差不能刻畫相依特征，分析人員需要更可靠的度量方法，如利用配對回歸函數m(t，h)。一般來說，這些函數的推斷需要用到窗寬選擇的非參數估計方法，限制了其應用范圍。基于測度論，回歸函數m(t，h)可以由單整回歸函數γt，h(x)表述：

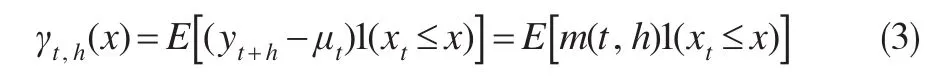
式(3)的推導依據是迭代期望定理，γt，h(x)測度稱為單整配對回歸函數(IPRF)，也可采用不同于示性權重1(xt≤x)的其他權重函數[7]。相依結構γt，h(x)的單整測度適于在非線性時間序列中檢驗感興趣的假設，與m(t，h)不同，它不需要平滑估計，并且很容易通過抽樣模擬估計。此外，它還刻畫了Granger給出的配對概念，并且使這些概念更易于操作。

令范數||||表示非遞減，如果對于所有函數 f和g，對 任 意 x都 有 |f(x)≤g(x)| ，則 | |f||≤| |g ||。 令 距 離d(f.g)=‖f-g‖。通常非遞減范數是L2范數和上確界范數。對于任意時間t，隨h逐漸增大時，‖γt，h(x)‖ ， h ＞ 0 趨于0，則稱序列{yt}是相對距離d配對SMM（PSMMd）。更準確的說，對于所有t，‖γt，h(x)‖ ＜c(h)，當 h 趨于無窮時，其中c(h)≡c(h，t)是趨于0的正序。如果{yt}不滿足上述條件，則稱為PEMMd。

基于以上概念，非線性協整定義如下：對于兩個PEMMd序列 yt和 xt，如果存在函數 f使得 zt=yt-f(xt)是PSMMd，那么序列yt和xt之間存在非線性協整關系。

2 非線性協整關系的檢驗

由上述定義可知，非線性協整關系的檢驗首先需要考察時間序列的平穩性問題，然后再對變量間是否存在非線性協整關系進行檢驗。但是經過經過非線性變換的時間序列生成結構將具有非線性特征，傳統的ADF等單位根檢驗方法已不再適用，Engle-Granger等協整檢驗方法也將以更高概率拒絕存在協整關系的原假設。

2.1 單位根檢驗

考慮到非線性結構對單位根檢驗的影響，當前在非線性協整分析中常用的單位根檢驗方法包括修正的ADF檢驗、秩檢驗方法以及全距單位根檢驗方法。

修正的ADF檢驗方法實際上是采用泰勒展開式對ADF統計量的分布以及檢驗臨界值進行修正，蒙特卡洛模擬表明修正后統計量的小樣本性質優于傳統的ADF檢驗。單位根的秩檢驗方法可以避免傳統的DF類型檢驗非線性持續性和離群值時的高度敏感性。我們更傾向于于提倡的方法是全距單位根檢驗(RUR)方法，即對序列一階差分后的全距進行檢驗。全距是時間序列在任一時間點極大值和極小值的差，因而全距的差異是對記錄的測度。對新的記錄數量計數，是一種區分時間序列平穩和非平穩很好的途徑，原因在于平穩序列新紀錄的頻率消失的要比具有單位根序列的更快。已有文獻證明了對于單調變換、誤差分布、結構突變和額外離群值的檢驗都比較穩健[8]。

2.2 非線性協整關系的檢驗

基于非線性協整關系的表述，對變量間非線性協整關系的檢驗主要是考察非線性模型的短記憶和長記憶特征，當前研究中常用的方法包括R/S檢驗和秩檢驗方法等。

R/S檢驗是檢驗記憶依賴強度的一種非參數方法。R/S統計量度量的是變量與均值離差的標準化全距，值越大表明記憶依賴性越強。雖然R/S統計量相對穩健，但是對于時間跨度較小的樣本檢驗功效較低。協整關系的秩檢驗方法首先在秩序列間進行差分，如果不存在協整，秩序列趨于發散，否則演化相似。記錄數協整檢驗(Record Counting Cointegration test,RCC)是在秩檢驗基礎上拓展的方法，將協整序列間的同步跳躍記錄數，也就是兩個序列同時發生跳躍的計數作為檢驗統計量。顯然，具有協整關系的序列同步跳躍的數量就會很大。對于單調非線性、結構突變以及那些不需要先驗估計量的線性和非線性協整函數檢驗，RCC都是比較穩健的[9]。

除此之外還有從信息理論角度進行協整關系檢驗的相關系數法，以及從頻域分析角度進行檢驗的李雅普諾夫指數法等。

2.3 非線性協整分布的測度

直觀上，在協整條件下對yt做長期的非線性預測時，極早期的xt應該與極早期的yt一樣重要。在線性假定下進行模擬，依據 γt，h(x)和隨 h趨于無窮小時的收斂速度，可以定義持續性和非線性協整的分布測度。對于分布相依，我們建議采用Kosfeld and Robe(2001)[10]給出的定義。令 ft，h(y，x)，kt+h(y)和 gt(x)分別表示yt+h和xt的二元和邊際密度。可以采用海林格距離定義：

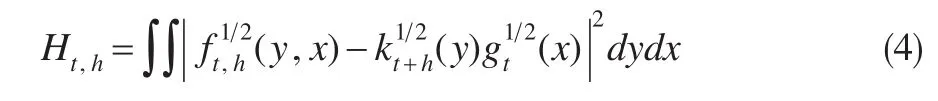
同時根據Ht，h隨h發散到無窮大時衰減到0，定義依分布配對短期記憶（PSMD）。分布持續性與混合概念關系密切。實際上，在均勻的時間 t上，Ht，h≤2α(h)，其中 α(h)即為一種α混合系數。

但是這種非線性分布持續性測度依賴于平滑估計，如核估計量Gouriéroux and Jasiak,2002)[11]。與條件均值測度相似，我們建議采用單整相依測度，而不用平滑，建立方程：

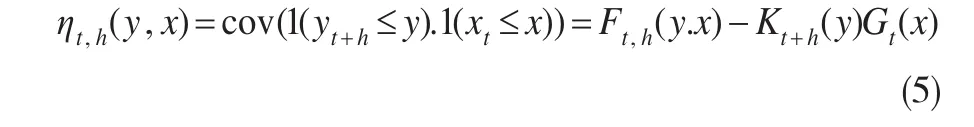
式(5)中 Ft，h(y.x)，Kt+h(y)以及 Gt(x)分別為 yt+h和 xt的二元和邊際累積分布函數。ηt，h(y.x)測度可以通過在不同的滯后值采用抽樣模擬進行估計，即經驗分布函數。進而可以推斷兩個依分布持續性的序列yt和xt在滿足下列條件時，是依分布非線性協整的：

3 非線性協整模型的推斷

非線性協整分析的建模過程主要包括五個步驟：第一檢驗變量間是否存在非線性協整關系；第二估計非線性協整函數 f，包括參數方法和非參數方法，這是非線性協整問題的重點和難點；第三檢驗zt=f(yt，xt)的短期記憶特征，也就是單位根檢驗；第四利用估計的非線性協整函數f構建非線性誤差修正模型，并估計參數；第五利用非線性協整模型的推斷結果進行預測。

3.1 參數方法

如果能夠確定非線性回歸函數的形式，則可以采用參數方法估計非線性協整函數。基于單整相依測度方法，我們建議采用具有單整回歸變量的非線性模型：

g(x-c，γ)通常采用 Logistic 函數形式 -1/(1+e-γ(x-c))。如果δ=0，回歸模型將退化為線性 yt=βxt+zt，此時修正非線性最小二乘估計結果是漸近有效的。式(7)為非線性回歸模型的特殊形式，基本形式可表示為：

xt是單整回歸變量，β為參數向量，vt是均值為0的平穩誤差項，f(xt，β)是時間序列xt的平滑函數。從傳統漸近理論角度看，雖然有的文獻嘗試了單指數型回歸的拓展，但已有研究還是都受限于模型中 p=1的情形，也就是向量 xt的結構中 (1，xt，xt-1，...，xt-p)，p 僅取到1。限于單變量情形的外在原因在于通常漸近理論并不適用于p＞1的情形，如基于當前時區(local time)的漸近技術不可能出現p＞2。問題的內在原因是當p＞2時，p元布朗運動的非復發性特征。同時在傳統漸近理論中，β估計量的特征，如非線性最小二乘估計量(NLSE)，依賴于 f(xt，β)所屬函數的具體類型。通常使用的函數類型是可積函數、漸近齊次函數和指數函數。

但是NLSE的收斂速度依賴于函數特定形式，在某些情況下涉及隨機尺度。為了處理隨機尺度，可以采用三角行列式漸近技術[12]，擺脫β估計量的收斂速度依賴于函數特定形式的難題。

3.2 非參數方法

在實際分析中，非線性回歸函數的形式通常是難以確定的。如果函數形式選擇有誤，接下來的參數估計和預測都將產生偏差。非參數方法不必假定模型的非線性回歸函數已知，利用樣本已有的信息展開對非線性協整函數 f的估計。常見的非參數方法包括神經網絡法、交替條件期望（ACE）算法以及非參數漸近方法等[13]。

神經網絡法是一種不需要事先選擇模型形式的非參數方法，其基本思想是將比較合理的變量間的非線性函數關系構建成一個廣義模型，利用遞歸算法逼近未知的非線性協整函數。Karlsen and Tj?stheim(2001)[14]采用零常返馬爾科夫進程理論進行非線性協整檢驗，相關研究極大的推動了非參數檢驗方法的發展。ACE算法實際上很早就出現在Granger的相關研究中，該方法不需要嚴格的分布假設，通過最小化回歸模型的期望均方誤差估計非線性轉換函數，其基本思想是利用非參數數據平滑技術，迭代計算直至均方誤差達到最小，進而獲得變量的最優轉換。

對基于單整相依測度方法表述的非線性協整關系，近單整非參數漸近方法是一種可行的途徑[15]，重點在于估計非線性回歸模型的轉移函數 f(xt)：

其中序列yt和xt是單變量可觀測非平穩過程，vt是不可觀測的平穩過程。 f(xt)的非參數核估計如下：

其中Kx，h(xt)=h-1K((y-x)/h)，K是核函數，h是窗寬參數。非平穩進程族通常被稱為β0常返馬爾科夫過程，滿足了經常性時間尾部分布的限制，可以處理的類型包括隨機游走、單位根過程以及非線性非平穩過程。與平穩狀態的非參數估計理論不同，非線性回歸轉移函數呈現出很慢的收斂速度，非參數漸近理論非常有利于非線性協整模型推斷理論的完善和發展。

4 總結與展望

在線性框架下，已有較完備的理論和工具研究協整問題，然而對非線性下的協整問題，還面臨著很大的挑戰。實現非線性擴展有兩種方法，一種是應用向量誤差修正模型，但仍然采用線性協整回歸。另一種方法是考慮非線性協整回歸方程。對于這兩種方法，我們建議采用可操作性較強的單整相依測度，因為該方法易于估計且不必對數據平滑。未來研究中很重要的一個研究方向就是對單整測度非線性協整推斷方法進行完善。

從當前的研究來看，傳統的線性協整方法在國內的宏觀及金融時間序列分析中仍占據主流地位，然而近10年來逐漸有越來越多的學者在對中國的經濟問題分析中采用非線性協整模型。通過對國內相關文獻的梳理可以發現，由于非線性協整函數選擇的不同而存在眾多不同形式的非線性協整模型，其中常用的包括閾值協整模型、馬爾科夫機制轉換模型以及平滑轉換機制模型等。在一些實證研究中可以發現利用非線性協整模型分析中國宏觀經濟和金融市場中變量間的關系[16]，揭示了原有線性分析框架下難以描述的動態特征，可以更加清晰的反映各種變量間的長期依賴關系和短期動態調整機制，有助于決策者有效的制定宏觀調控政策。但是這幾類典型模型僅體現了非線性協整理論的部分內容，非線性協整函數的估計和選擇是未來研究的重點和難點。

在內生和平穩的前提下，分析非線性時間序列模型相對容易，但拓展到非平穩性時，當前計算方法仍存在不足。特別的，對于非平穩變量進行非線性轉換的傳統漸近分析結果依賴于函數的特定形式，并且只能分析單變量的情形[17]。未來研究的另一個重要方向就是將漸近分析拓展到多元變量的框架下，并進一步完善計算方法。

[1]王少平.宏觀計量的若干前沿理論與應用[M].天津:南開大學出版社,2003.

[2]Tong H.Non-linear Time Series:A Dynamical Systems Approach[M].Oxfod:Oxfod University Press,1990.

[3]Balke S,Fomby B.Threshold Cointegation[J].International Economic Review,1997,（38）.

[4]Granger C W J.Modeling Nonlinear Relationships Between Extended-Memory Variables[J].Econetrica,1995,63(2).

[5]雷欽禮.非線性協和模型：理論與方法[J].統計研究,2009,26(3).

[6]Leybourne S J,Taylor A M R.Persistence Change Tests and Shifting Stable Autoregressions[J].Economics Letters,2006,91(1).

[7]Escanciano J C,Velasco C.Testing The Martingale Difference Hypothesis Using Integrated Regression Functions[J].Computational Statistics and Data Analysis,2006,51(4).

[8]Aparicio F,Escribano A,Sipols A E.Range Unit-Root(RUR)Tests:Robust Against Nonlinearities,Error Distributions,Structural Breaks and Outliers[J].Journal of Time Series Analysis,2006,27(4).

[9]Escribano A,Sipols A E,Aparicio F.Nonlinear Cointegration and Nonlinear Error Correction:Record Counting Cointegration Tests[J].Communications in Statistics,Simulation and Computation,2006,35(4).

[10]Kosfeld R,Robe S.Testing For Nonlinearities in German Bank Stock Returns[J].Empirical Economics,2001,26(3).

[11]Gouriéroux C,Jasiak J.Nonlinear Autocorrelograms:An Application To Inter-Trade Durations[J].Journal of Time Series Analysis,2002,23(2).

[12]Choi I,Saikkonen P.Tests For Non-Linear Cointegration[J].Econometric Theory,2010,26(3).

[13]張世英,樊智.協整理論與波動模型—金融時間序列分析及應用[M].北京:清華大學出版社,2004.

[14]Karlsen H A.Semiparametric Regression Estimation in Null Recurrent Nonlinear Time Series[J].Annals of Statistics,2001,29(2).

[15]Krusea R.Long Memory and Changing Persistence[J].Economics Letters,2012,114(3).

[16]王少平,歐陽志剛.中國城鄉收入差距對實際經濟增長的閾值效應[J].中國社會科學,2008，(2).

[17]Granger C W J.Some Thoughts on The Past and Future of Cointegration[J].Journal of Econometrics,2010,158(1).