中心極限定理在統計推斷中的應用

丁 健，李紅菊

(安徽新華學院公共課教學部，安徽合肥230088)

在經濟數學的實際問題中，隨機變量到處可見，許多隨機變量服從正態分布，即使有些隨機變量不服從正態分布，但它們的和也近似服從正態分布，這是由中心極限定理決定的.在概率論中凡是在一定條件下判定隨機變量之和的分布是正態分布的定理統稱為中心極限定理.中心極限定理解釋了正態分布廣泛存在的原因，并為解決實際問題時利用正態分布提出了理論依據.目前教科書上僅對中心極限定理做了理論上的闡述，對它的實用價值涉及較少，本文通過統計推斷中的實際問題來說明中心極限定理的廣泛應用.通過對實際問題的探討和學習，學生能夠較深刻地理解和掌握中心極限定理，這對教學有實際意義.

1 中心極限定理

獨立同分布的中心極限定理和棣莫弗－拉普拉斯中心極限定理是我們所熟悉的兩大類中心極限定理，具體內容如下:

獨立同分布的中心極限定理［1］設隨機變量 X1，X2，…，Xn相互獨立，且服從同一分布，E(Xi)=u，D(Xi)= σ2，i=1，2，…，n，則當 n 很大時，隨機變量，即

棣莫弗 －拉普拉斯中心極限定理［1］在n重伯努力試驗中，事件A在每次試驗中發生的概率為p，ηn為事件A發生的次數，則當n充分大時，有或

2 中心極限定理的實際應用

2.1 中心極限定理在統計估計中的應用

數理統計一般研究正態總體均值和方差的統計估計，而由簡單隨機抽樣得到的隨機變量是相互獨立且服從同一分布的，所以在實際問題中，不論總體服從什么樣的分布，只要樣本的容量充分大，我們就可以根據中心極限定理把隨機變量的和近似看成服從正態分布，直接利用中心極限定理進行統計推斷，對總體中未知參數進行區間估計.

不論總體服從什么分布，只要選擇的樣本容量足夠大，根據中心極限定理，樣本均值為選取樞軸量關于總體均值的置信水平為1－α的置信區間為在許多實際問題中，我們還經常碰到總體分布和總體方差均未知的情況，此時可以用樣本方差s2作為總體方差D(X)的無偏估計量，用s2代替D(X)，根據中心極限定理，仍可以求出μ的置信水平為1－α的置信區間

例1 以X表示某一工廠生產的某種器材的壽命(以小時計)，經驗表明D(X)=1156，現從總體中取得一容量為49的樣本，得到各個觀察值，并計算出樣本均值珋x=1589，樣本方差s2=1122.25.求總體均值μ在置信水平為0.95時的置信區間.

解 由題意可知，從總體中抽取了一個大樣本(n=49)，不論總體服從什么樣的分布，根據中心極限定理，樣本均值

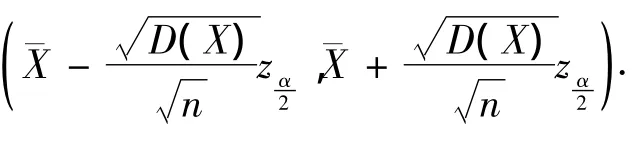
1－α=0.95，總體均值μ的置信水平為0.95的置信區間為查正態分布表得.代入觀察值得到這家工廠制造的器件平均壽命的置信水平為0.95的置信區間為(1579.48，1598.52)，這說明這家工廠制造的器件平均壽命在(1579.48，1598.52)的概率不小于0.95.

注 如果在例1中不知總體的方差，仍可以計算出總體均值μ的置信水平為0.95的置信區間

如果試驗是伯努力試驗，隨機事件A發生的概率p未知，可以從總體中抽取一個容量(n)很大的樣本，fn表示事件A發生的次數。當樣本容量很大時，二項式分布近似于正態分布，即)，對 p進行統計估計，則關于p的置信水平為1－α的置信區間為

例2 糧站有一大批糧種，欲了解糧種的發芽率p，在其中任選了6400粒進行試驗，試驗結果5000粒發芽，求糧種發芽率p的置信水平為0.99的置信區間.

1－α=0.99，得到發芽率p在置信水平為0.99時的置信區間為

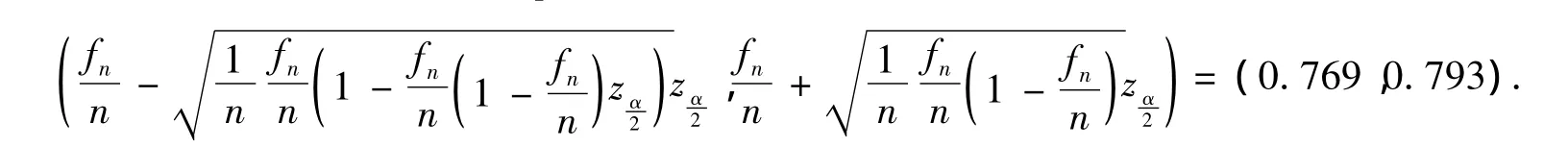
2.2 中心極限定理在假設檢驗中的應用

假設檢驗是統計推斷的另一個重要內容.對總體分布函數的形式或關于總體參數值的陳述叫做統計假設［1］.總體的分布或參數未知的情況下，通過一些預知的知識對總體提出兩個假設H0和H1，然后根據樣本去判斷是接受H0還是拒絕H0的過程是假設檢驗［1］.

在許多實際經濟問題中，研究的幾乎都是大樣本．根據中心極限定理，當樣本容量很大時，對總體的均值進行假設檢驗，提出原假設 H0:E(X)=μ0，可以選取檢驗統計量或，當原假設H0成立時，檢驗統計量Z近～似N(0，1)，選擇顯著性水平為α，此時H0的拒絕域為

例3 某農業大學研究在改善栽培條件下黃豆的重量是否有明顯改變，已知改善條件前黃豆的平均重量μ0=350(單位:mg)，σ未知，現隨機地抽取100粒，測得這100粒黃豆的平均重量x珋=352.5mg，s2=25，問在顯著性水平α=0.05條件下改善栽培條件后黃豆的重量是否較之前重量有明顯差異?

解 由題意H0:E(X)= μ0;H1:E(X)≠μ0，其中μ0=350.

在顯著性水平 α=0.05的條件下，H0的拒絕域為|Z|≤zα=Z0.025.

查正態分布表z0.025=1.96，故|Z|=，所以接受原假設，即認為在顯著性水平α=0.05的條件下改善栽培條件后黃豆的重量較之前重量有明顯差異.

3 結語

由于實際的經濟問題均通過大樣本來估計總體，總體的分布已知不是必要的解題條件，只要當樣本容量很大，隨機變量的和總是近似服從正態分布，正是這個結論使得中心極限定理可以解決很多實際問題.本文僅探討了中心極限定理在統計推斷中關于總體未知參數的區間估計和假設檢驗的一些實際應用，其實在商業管理決策、函數極限求法、保險業、抽樣推斷中的概率預測和樣本容量的確定等實際問題中都會用到中心極限定理，所以對于中心極限定理的研究具有一定的理論意義和實際價值.

［1］盛驟，謝式千.概率論與數理統計及其應用［M］.北京:高等教育出版社，2010.

［2］劉家琨.應用概率統計［M］.北京:科學出版社，2004.