船體梁極限強度非線性有限元計算方法研究

張津寧 吳劍國

（浙江工業大學 建工學院 杭州310014）

引 言

非線性有限元法（NFEM）是計算和分析船體極限承載能力的強有力工具，它不僅可獲取船體承載能力的極值，而且可通過追蹤整個失穩過程中實際的荷載與位移關系獲得結構失穩前后的全部信息。近幾年來，隨著計算機技術的飛速發展，一些大型的通用有限元程序（如ANSYS、ABAQUS、MSC MARC，MD NASTRAN等），均被應用于船舶結構的極限強度計算，并得到一些成功的案例［1-4］，但非線性有限元計算的效率和精度很大程度需取決于建模技術的合理性。在CSR-H規范第1篇第5章附錄2中規定可采用非線性有限元方法作為船體梁極限強度分析的一種替代方法使用，但在規范中并未對有限元分析過程中的模型大小、網格劃分、邊界條件和初始缺陷等因素進行明確的規定，所以對船體梁極限強度非線性有限元計算方法進行研究很有必要。

本文采用ABAQUS軟件對 Dow 1/3 的比例護衛艦模型的船體梁極限強度進行計算，計算模型及中垂極限狀態下應力云圖見圖1和圖2；通過與Smith方法和模型試驗所得結果進行對比和分析，研究非線性有限元建模技術中各個因素對計算結果的影響；提出一種較為準確高效的船體梁極限強度非線性有限元計算方法。

圖1 計算模型

圖2 中垂極限狀態下應力云圖（放大50倍變形）

1 試驗模型

Dow 等［5］以一條 Leander 級的護衛艦為原型，以 1/3 的比例建立一個焊接船體模型進行崩潰試驗（見圖3）。模型施加中垂彎矩從而模擬實船的中垂狀態。試驗結果發現甲板及舷側板上部分結構的屈曲導致剖面的全面崩潰，試驗得到中垂狀態承載能力值為9.64 MN·m，曲線見圖4。

2 非線性有限元建模技術研究

2.1 模型大小

圖3 實驗模型結構形式和尺度

圖4 中垂狀態彎矩曲率圖

采用非線性有限元方法計算船體梁極限強度的過程中通常可選取單跨模型、多跨模型、一艙段模型等三種模型。通常情況下，加大計算模型在船長方向長度可更準確模擬模型破壞部分的邊界條件，但加長模型的同時也會大幅增加模型的單元數目，進而降低計算效率且增加計算成本。

本文推薦選取船舯部分兩個強框架之間的結構建立模型。這是因為在通常情況下，彎矩作用下船體梁的破壞形式是強框架之間加筋板的局部屈曲。所以認為在合理選取邊界條件的前提下可以采用兩個強框架范圍內構件模型來計算船體梁極限強度。另一方面橫向構件本身并不參與總縱彎矩的承載，研究發現有無橫向構件對極限彎矩的影響很小。所以在計算過程中可近似認為橫向構件所在平面是一個剛性面，進而使用約束條件替代橫向構件。

2.2 單元類型

由于船體梁的極限強度和屈曲有關，因此采用板單元模擬板格、加強筋腹板和面板，所得結果更準確。但如果在多跨模型和一艙段模型中使用板單元來模擬加強筋面板，會極大地增加模型網格劃分的難度。所以在多跨模型和一艙模型中可以使用梁單元來模擬加強筋的面板。在ABAQUS軟件中，通常使用S4R縮減積分殼單元和S4完全積分殼單元來進行弧長法以及準靜態法的計算。研究表明兩種單元所得極限強度和應力分布都基本一致。

2.3 網格密度

有限元分析中控制計算量的主要因素包括網格的疏密。控制網格密度最主要的因素是對于結構幾何非線性的考慮，其最基本要求是單元的尺度不能大于屈曲半波長度的一半。船體梁有限元模型網格劃分過程中要考慮有限元網格密度應該大到足以模擬板、扶強材、縱桁、艙壁、底板、甲板等這些結構所有相關的局部屈曲變形和局部塑形破壞。本文采用三種不同網格密度分別對三分之一護衛艦模型的極限強度進行計算。三種網格密度見圖5。

圖5 網格密度

圖5中：

（1）網格A

相鄰兩個加強筋之間板材劃分6個網格；加強筋腹板劃分3個網格；加強筋翼緣劃分2個網格。

（2）網格B

相鄰兩個加強筋之間板材劃分10個網格；加強筋腹板劃分6個網格；加強筋翼緣劃分6個網格。

（3）網格C

相鄰兩個加強筋之間板材劃分19個網格；加強筋腹板劃分6個網格；加強筋翼緣劃分2個網格。

通過對比可以發現：板材劃分網格相對較密的網格C模型的計算結果更接近實驗值；三種不同網格密度的有限元模型計算結果比較接近，網格C模型的計算結果相對于網格A模型的計算結果下降約4%。計算結果見圖6和表1。

圖6 不同網格模型極限強度中垂狀態

表1 中垂狀態下不同網格模型極限強度對比

船體梁的破壞主要源于加筋肋之間的板材發生局部屈曲，所以當板材劃分網格相對較密時所得的有限元計算結果更為精確。此外，可以發現三者計算結果比較接近，但網格C模型的計算量遠大于模型A。所以在實際研究過程中，使用A類型網格密度是合理高效的。

2.4 初始缺陷

有限元計算的另一個優勢也在于能在分析結構極限強度的過程中引入初始缺陷和殘余應力的影響。本文通過計算討論初始缺陷對船體梁極限強度的影響。

初始缺陷的一般經驗公式：板的初始屈曲撓度

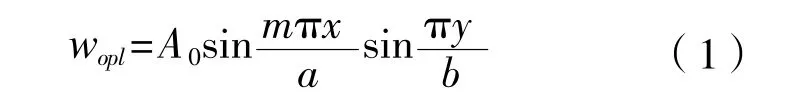
加強筋縱向初始變形

加強筋橫向初始變形

其中板的屈曲模式m取滿足公式時m的最小值，各參數見表2。

表2 初始缺陷的幅值

分別對以下三種有限元模型進行計算，三種計算模型見圖7。

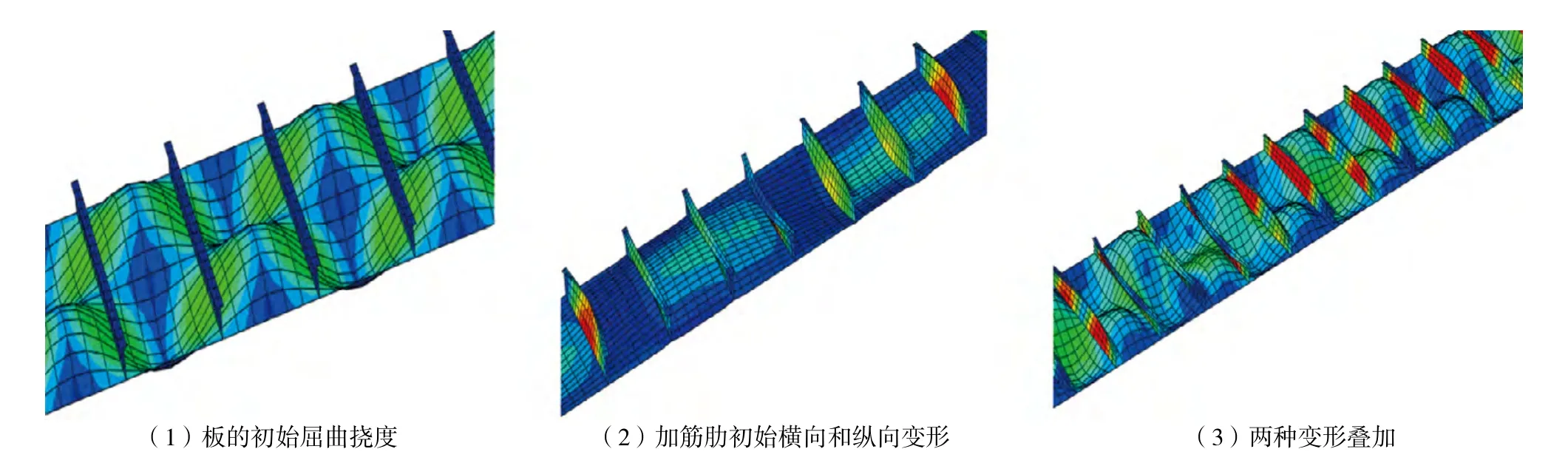
圖7 初始缺陷（放大50倍）

（1）引入板的初始屈曲撓度模型；

（2）引入加筋肋初始橫向和縱向變形模型；

（3）兩種變形疊加模型。

計算結果及對比見圖8和下頁表3。可以發現，初始缺陷對船體梁極限強度的影響較小，其中加筋肋的初始變形是主要因素。但應注意到在非線性計算過程中，引入初始缺陷對計算結果的收斂性有積極的貢獻。

2.5 邊界條件

圖8 不同初始缺陷模型極限強度中垂狀態

表3 中垂狀態下不同初始缺陷模型極限強度對比

有限元計算和分析過程中計算結果的準確程度很大程度上受邊界條件的影響。在船體梁極限強度的計算過程中，選取邊界條件首先需保證模型的邊界符合平斷面假設，即模型端部的所有點始終處于一個平面內。本文采用的邊界條件：

（1）固支邊界。一端固定，所有點與對應中性點耦合后施加彎矩。

（2）簡支邊界。模型兩個端面的所有點與對應中性點耦合，進一步使一端耦合點X、Y、Z方向位移固定，X方向轉角固定。另一端耦合點Y、Z方向位移固定。在兩個耦合點上加對稱彎矩。

計算結果見圖9和表4。通過對比可以發現，相比常用的一端固定一端施加彎矩的邊界條件，簡支邊界條件更接近實際情況。

圖9 不同邊界條件模型極限強度中垂狀態

表4 中垂狀態下不同邊界條件模型極限強度對比

2.6 分析方法

目前船體梁極限強度有限元計算中的主要分析方法有靜力法、弧長法和準靜態法。對于同時具有幾何非線性和材料非線性的模型，采用靜力法計算往往難以取得精確的極值。準靜態法的基本思想是將模型在加載的過程中任意時刻所經歷的中間狀態都大致視為靜力狀態，因此當加載過程進行得無限緩慢時，在各個時刻模型所處的狀態就可大致看作是靜態，該過程便是準靜態過程。

在很多情況下，準靜態法比靜力法更易求解，但準靜態法需要大量的時間增量步，因此計算效率相對較低。弧長法的優勢在于可以考慮剛度奇異的失穩點附近的平衡，而且可以通過追蹤整個失穩過程中實際荷載、位移關系獲得結構失穩前后的全部信息，且在相同情況下，其計算增量步遠小于準靜態法。

2.7 殘余應力

ISSC（2012）［6］綜合多項研究表明，殘余應力對船體梁極限強度的影響較小，并且焊接殘余應力對船體梁極限強度的影響發生在船舶建造初期，隨著船舶的營運，焊接殘余應力逐漸減小，周期一般在3個月左右。為較好地描述殘余應力，需建立實體單元的精細模型，比如扶強材之間就需要50多個單元，這對于船體梁模型是不可想象的。 因此，本文模型中不考慮殘余應力。殘余應力的影響通常放在準則的模型不確定之中加以考慮。

2.8 推薦模型

本文采用非線性有限元軟件ABAQUS對Dow 1/3 比例護衛艦構件模型的極限彎矩進行計算，模型材料選用屈服應力為245 MPa的鋼材。非線性計算時采用雙線性模式，其中應變硬化參數取1 000 MPa。模型兩端加對稱彎矩從而模擬船舯剖面的純彎破壞。計算過程中選用弧長法作為迭代控制方法。計算得到中垂狀態下彎矩曲率曲線極值（極限中垂彎矩）11.14 MN·m，見圖4。

綜上所述，本文推薦采用一種較合理的船體梁非線性有限元計算方法。應關注以下幾點：

（1）模型大小

單跨模型，即兩個強框架之間的結構模型（不包括強框架）。

（2）應力-應變關系

雙線性模式，其中應變硬化參數取1 000 MPa。

（3）網格密度

相鄰兩個加強筋之間板材劃分6個網格；加強筋腹板劃分3個網格；加強筋翼緣劃分2個網格。

（4）邊界條件

簡支梁模式的邊界條件，即采用耦合條件剛化模型兩個端面，取耦合點為簡支梁兩個端點，施加約束條件。

（5）分析方法

弧長法。

（6）初始缺陷

初始缺陷對船體梁極限強度的影響較小，但采用弧長法計算時引入初始缺陷更易求解。

3 結 論

本文通過計算和分析，提出一種較為準確高效的船體梁極限強度非線性有限元計算方法。我們采用上述方法完成了 10多艘大型運輸船船體梁極限強度計算，對于完善《船體梁極限強度的非線性有限元方法計算指南》具有一定的參考價值。

［1］ Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression-nonlinear finite element method investigations［J］.Ocean Engineering，2009，36：266-276.

［2］ Do Kyun Kim，Dong Hee Park.Lateral pressure effects on the progressive hull collapse behavior of a Suezmaxclass tanker under vertical bending moments［J］.Ocean Engineering，2013，63：112-121.

［3］ 王軍，孫豐，陳舸，等.船體典型結構局部強度考核試驗模型設計［J］ .船舶，2013（6）：40-46.

［4］ 湯紅霞，王曉宇，劉見華，等.艦船結構極限強度計算及試驗研究［J］.船舶，2014（3）：26-29.

［5］ Dow R S.Testing and analysis of 1/3-scale welded steel frigate model［A］.Proc.Of Intl.Conf.On Advances in Marine Structures，Dunfermline，U.K.，1991 ：749-773.

［6］ ISSC Ultimate strength［C］.Report of 18th International Ship And Offshore Structures Congress，2012-09：285-363.