基于總體最小二乘的多基地聲納系統(tǒng)定位算法

李 濤，屈也頻，梅風(fēng)華

（海軍裝備研究院航空裝備論證研究所，上海 200436）

0 引言

多基地聲吶定位技術(shù)由于其在覆蓋范圍、定位精度、抗隱身能力和戰(zhàn)術(shù)使用上的優(yōu)勢(shì)，已成為現(xiàn)階段聲吶技術(shù)領(lǐng)域研究的熱點(diǎn)［1-2］。現(xiàn)有的多基地聲吶系統(tǒng)通過(guò)獲得目標(biāo)的方位角、距離和多普勒頻移等測(cè)量結(jié)果，結(jié)合目標(biāo)與多基地聲納的相對(duì)位置關(guān)系解算出目標(biāo)坐標(biāo)［3-7］，但這種算法受測(cè)量誤差影響，在某些區(qū)域定位性能非常差。在多基地情形下，利用不同接收站的測(cè)量信息存在數(shù)據(jù)冗余的特點(diǎn)，充分利用各個(gè)接收站所獲得的測(cè)量數(shù)據(jù)可以改善這種現(xiàn)象［8］，文獻(xiàn)［9］和［10］則從提高測(cè)量信息利用率的角度，分別研究了基于卡爾曼濾波的單枚、多枚被動(dòng)定向浮標(biāo)定位算法，但共同的缺點(diǎn)是需已知測(cè)量信息的誤差模型。針對(duì)常規(guī)解算法進(jìn)行多基地聲納系統(tǒng)定位時(shí)，定位精度和穩(wěn)健性受測(cè)量誤差影響嚴(yán)重的問(wèn)題，提出基于總體最小二乘法的多基地聲吶定位算法。

1 多基地定位原理

以T-R3型多基地聲吶系統(tǒng)為例，考慮到聲納作用距離通常要高出探測(cè)目標(biāo)深度一個(gè)數(shù)量級(jí)以上，即目標(biāo)的垂直向的俯仰角很小，故只在水平坐標(biāo)內(nèi)考慮定位，以發(fā)射站為原點(diǎn)建立二維直角坐標(biāo)系，各基站的幾何關(guān)系如圖1所示。

根據(jù)圖1所示的幾何關(guān)系，可得目標(biāo)的定位方程如式（1）。

式（1）中，ρi=vτi，為發(fā)射站與第i個(gè)接收站之間的傳播距離，v為水中聲速，τi為發(fā)射站與接收基站之間的傳播延時(shí)，通過(guò)收發(fā)基地時(shí)間同步后，可以實(shí)現(xiàn)時(shí)延的測(cè)量。易知具有相同ρi 的目標(biāo)的軌跡集合構(gòu)成等時(shí)到達(dá)橢圓；θi由浮標(biāo)定向測(cè)出，具有相同θi的目標(biāo)軌跡集合構(gòu)成過(guò)接收站點(diǎn)的直線。易知式（1）方程組存在雙解，為消除模糊性，實(shí)際情況下可以通過(guò)附加浮標(biāo)作用距離信息、多址數(shù)據(jù)融合以及目標(biāo)軌跡連續(xù)等方法予以消除。

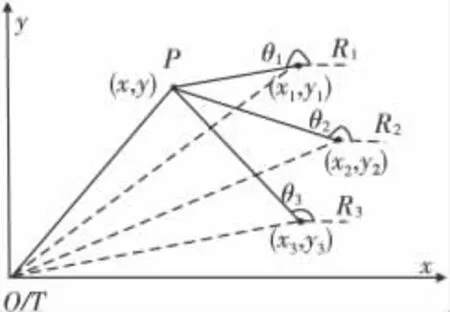
圖1 多基地聲納系統(tǒng)定位原理Fig.1 Position principle of multistatic sonar

由于ρi、θi及xi、yi均存在測(cè)量誤差，式（1）的解算結(jié)果會(huì)出現(xiàn)誤差，甚至無(wú)解，這在目標(biāo)靠近發(fā)射站與接收站連線（基線）時(shí)會(huì)更加突出，這是由于此時(shí)式（1）的第一個(gè)方程由于測(cè)距誤差的存在而不成立所致。當(dāng)存在多個(gè)接收站同時(shí)檢測(cè)到目標(biāo)時(shí)，可通過(guò)信息綜合處理技術(shù)提高定位精度，最簡(jiǎn)單的情況是對(duì)各個(gè)接收站的解算結(jié)果取平均

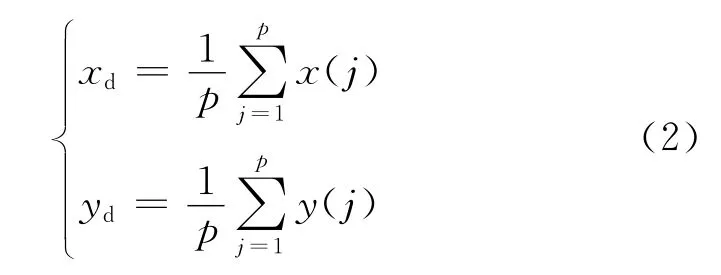
式（2）中，x（j）、y（j）為第i個(gè)有效接收站方程的解，xd、yd為綜合后的解算結(jié)果，p 為存在有效解的接收站數(shù)目。

2 基于總體最小二乘的定位算法

式（1）、式（2）的定位算法受ρi、θi及xi、yi的測(cè)量誤差影響較大，在多個(gè)接收站同時(shí)檢測(cè)到目標(biāo)的情形下，由于存在冗余探測(cè)信息，為了綜合利用不同接收站的測(cè)量信息，引入總體最小二乘方法來(lái)解決目標(biāo)定位問(wèn)題，其實(shí)現(xiàn)原理為：將測(cè)量方程進(jìn)行一定的數(shù)學(xué)變換，消去二次項(xiàng)，得到一組新的線性方程組。線性方程組的總體最小二乘解就是目標(biāo)的位置估計(jì)。

將式（1）消去二次項(xiàng)得

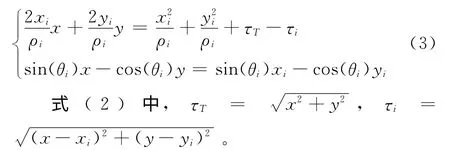
利用兩個(gè)接收站的測(cè)量結(jié)果消去未知量τT、τi，可得

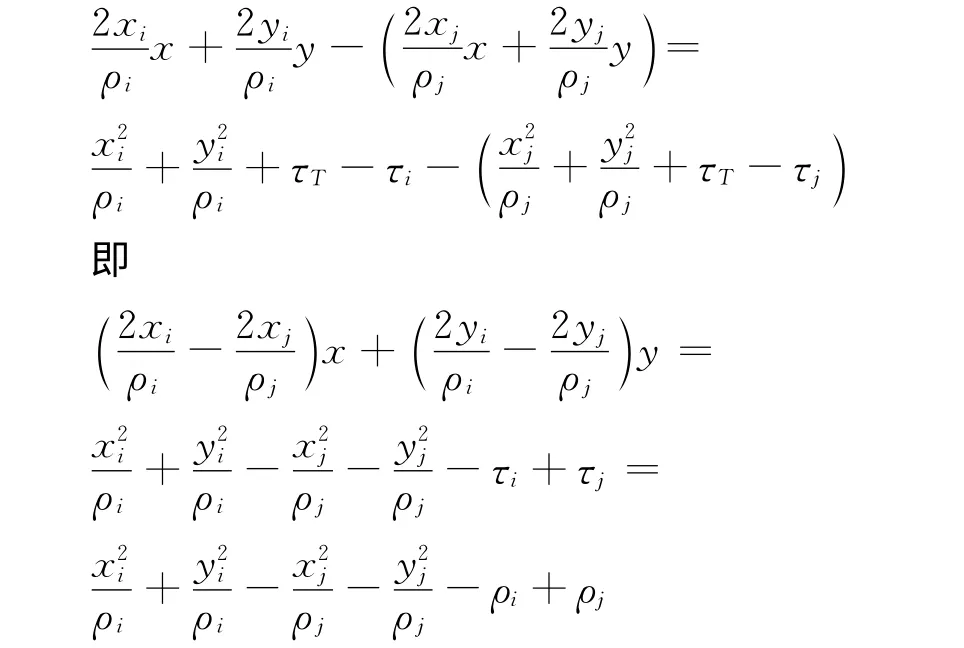
因此，利用多個(gè)接收站的測(cè)量結(jié)果可以建立線性方程組

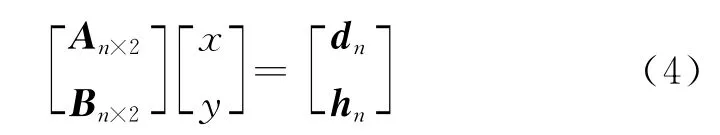
其中An×2、Bn×2為n×2維矩陣，dn、hn為n 維向量，n為接收站數(shù)目，且

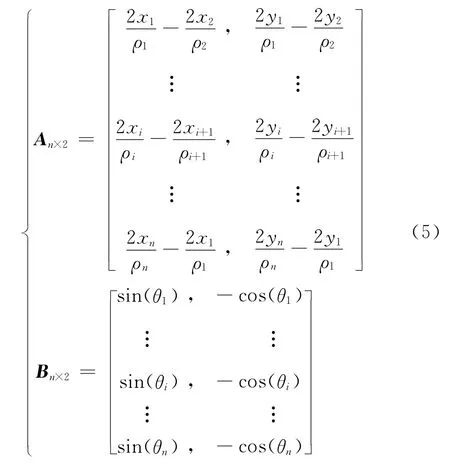
式（4）實(shí)際上是一組超定方程，通常可以通過(guò)最小二乘法來(lái)求解。觀察式（5）和式（6），由于ρi、θi及xi、yi均存在測(cè)量誤差，導(dǎo)致An×2、Bn×2及dn、hn均存在誤差，由于最小二乘法求解的過(guò)程只考慮將dn及hn的誤差最小化，不適合An×2、Bn×2均存在誤差的情形，因此下面基于總體最小二乘算法來(lái)求解式（4）。

將式（4）改寫(xiě)為：

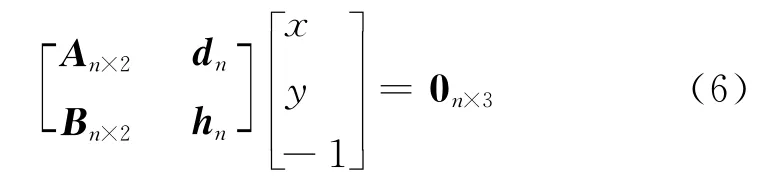
令

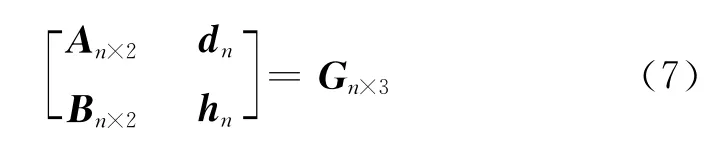
總體最小二乘法的求解過(guò)程即考慮誤差矩陣En×3，使得解，取最小特征值對(duì)應(yīng)的特征向量u，則

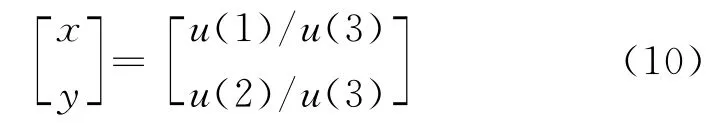
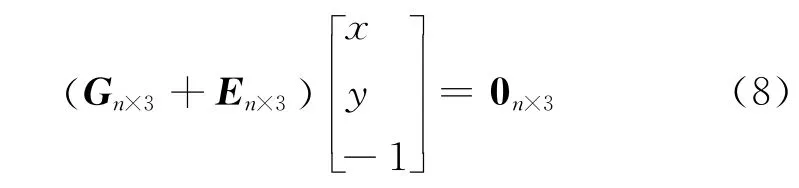
1）確定初始值u0、a，其中u0為任意3維向量

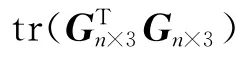
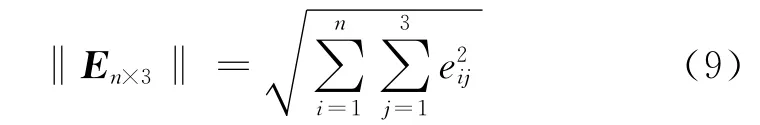
可見(jiàn)總體最小二乘法考慮的是將An×2、Bn×2及dn、hn的總體誤差最小化，因而更適 合式（4）的求解。

求解總體最小二乘解需對(duì)GTn×3Gn×3進(jìn)行特征分

3 計(jì)算機(jī)仿真

仿真試驗(yàn)通過(guò)式（1）、式（2）的直接解算法和基于冪迭代的總體最小二乘法來(lái)比較驗(yàn)證。

試驗(yàn)1 設(shè)接收站個(gè)數(shù)為3，接收站坐標(biāo)（5.4km，-8.4 km）、（10 km，0）、（5.4 km，8.4km），目標(biāo)坐標(biāo)為（5km，2km），浮標(biāo)散布范圍分別服從100 m、1 000 m 和2 000 m 內(nèi)的均勻分布，測(cè)向和測(cè)距誤差服從正態(tài)分布，對(duì)不同測(cè)向和測(cè)距方差下的定位方差進(jìn)行1 000次蒙特卡羅仿真，圖2給出了仿真的結(jié)果。

圖2的結(jié)果顯示，直接解算法在測(cè)距誤差及浮標(biāo)散布范圍增大時(shí)定位誤差迅速增大，顯示其對(duì)測(cè)距誤差和浮標(biāo)散布范圍非常敏感。采用總體最小二乘法較之直接解算法具有更好的定位精度，且穩(wěn)定性遠(yuǎn)高于直接解算法，尤其是在測(cè)距誤差及浮標(biāo)散布范圍較大時(shí)，總體最小二乘法顯示出抑制誤差的優(yōu)異性能。

試驗(yàn)2 設(shè)接收站個(gè)數(shù)為3，接收站坐標(biāo)（5.4km，-8.4 km）、（10 km，0）、（5.4 km，8.4km），改變目標(biāo)坐標(biāo)為（9.5km，0.5km），此時(shí)，目標(biāo)更加接近發(fā)射站與接收站連線。設(shè)浮標(biāo)散布范圍分別服從100m、1 000m 和2 000m 內(nèi)的均勻分布，測(cè)向和測(cè)距誤差服從正態(tài)分布，對(duì)不同測(cè)向和測(cè)距方差下的定位方差進(jìn)行1 000次蒙特卡羅仿真，圖3給出了仿真的結(jié)果。

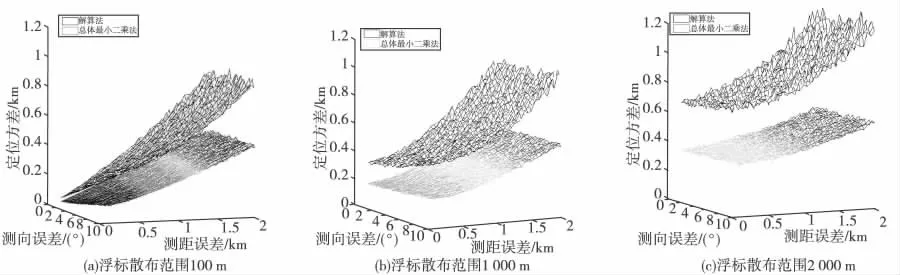
圖2 給定浮標(biāo)散布范圍時(shí)不同測(cè)向和測(cè)距誤差下的定位方差Fig.2 Positionvariance for different direction and distancemeasure error when specify buoy spread area

圖3 給定浮標(biāo)散布范圍時(shí)不同測(cè)向和測(cè)距誤差下的定位方差（目標(biāo)靠近基線）Fig.3 Positionvariance for different direction and distance measure error when specify buoy spread area（target near baseline）

圖3顯示結(jié)果與實(shí)驗(yàn)1相似，總體最小二乘法較之直接解算法具有更好的精確性和穩(wěn)定性。同時(shí)，由于目標(biāo)處在基線附近，采用式（1）解算時(shí)，會(huì)出現(xiàn)無(wú)解的情形，且出現(xiàn)無(wú)解情形的頻數(shù)隨測(cè)距誤差的增大而增大，但采用總體最小二乘法時(shí)，由于其能很好的擬合測(cè)量數(shù)據(jù)，即使是目標(biāo)處在基線附近且測(cè)距誤差較大的情形，依然能夠取得很好的定位精度，具有更好的穩(wěn)健性。

4 結(jié)論

本文提出了基于總體最小二乘法的多基地聲納系統(tǒng)定位算法，該算法首先將測(cè)量方程進(jìn)行一定的數(shù)學(xué)變換，得到一組新的線性方程組。通過(guò)求解線性方程組的總體最小二乘解估計(jì)目標(biāo)位置。仿真表明較之常規(guī)的解算法能夠取得更好的定位精度和穩(wěn)定性，同時(shí)解決了目標(biāo)處在基線附近，常規(guī)解算法隨測(cè)距誤差的增大而會(huì)出現(xiàn)無(wú)解情形的問(wèn)題。

［1］Coraluppi S.Multistatic sonar localization［J］.IEEE Journal of Oceanic Engineering，2006，31（4）：964-974.

［2］Sergey S.Localization in airborne multistatic sonars［J］.IEEE Journal of Oceanic Engineering，2008，33（3）：278-288.

［3］胡柱喜，孫明太，蘇維國(guó).被動(dòng)定向浮標(biāo)LOFIX 定位精度分析［J］.電光與控制，2009，16（12）：26-29

［4］孔銀壘，王英民.DIFAR 浮標(biāo)反正切目標(biāo)方位估計(jì)方法［J］.聲學(xué)技術(shù)，2010，29（4）：370-373

［5］王雋，王英民，陶林偉.浮標(biāo)定位算法的仿真研究［J］.聲學(xué)技術(shù)，2009，28（6）：95-98

［6］楊蕾.被動(dòng)型聲納浮標(biāo)定位技術(shù)研究［D］.哈爾濱：哈爾濱工程大學(xué)，2009.

［7］白菊蓉，毛永毅，張寶軍.多基地雷達(dá)空間定位算法和精度比較［J］.西安郵電學(xué)院學(xué)報(bào)，2008，13（1）：18-21.

［8］侯志國(guó)，何強(qiáng)，羅曉松.聲探測(cè)多傳感器多目標(biāo)定位與跟蹤方法［J］.電聲技術(shù)，2010，34（9）：40-42.

［9］陶林偉，王英民.一種新的單枚被動(dòng)定向浮標(biāo)目標(biāo)定位方法［J］.兵工學(xué)報(bào)，2011，32（3）：365-369

［10］陶林偉，王英民.基于擴(kuò)展卡爾曼濾波的DIFAR 浮標(biāo)陣定位算法及分析［J］.西北工業(yè)大學(xué)學(xué)報(bào)，2009（5）：738-744