基于飛輪儲能系統的無軸承無刷直流電動機內模控制

王 沖

(江蘇財經職業技術學院，淮安223003)

0 引 言

隨著科技和工業的發展，汽車作為方便快捷的代步工具已經走進千家萬戶。據統計，我國汽車保有量已經超過1.4 億輛，隨之也帶來能源危機和環境污染兩大不可忽視的問題。因此，開發高性能的儲能系統和清潔的新能源汽車對于我國生態文明建設和可持續發展都具有重要的意義。儲能系統作為電動汽車的能量轉換裝置是不可或缺的一部分。相比于傳統的蓄電池，飛輪儲能系統以其比能量高、壽命長、無污染、免維護等特點，得到了各國學者的青睞［1］。但是傳統軸承因為存在摩擦磨損，會對飛輪儲能系統的進一步發展產生一定的制約。相比于單純使用磁軸承支承，新型的無軸承電機將電機與磁軸承集成一體，不僅克服了磁軸承軸向空間長、結構復雜等不足，還具有轉速高、壽命長、免維護、無需潤滑和密封等優點，更適合作為飛輪儲能系統的驅動電機［2］。文獻［3］設計了一種應用于飛輪儲能系統的無鐵心無軸承電機/發電機，并對電機轉矩和懸浮力進行了有限元分析。文獻［4］提出一種外轉子型的無軸承永磁同步電機/發電機，飛輪直接安裝在外轉子表面;并設計了樣機，進行了轉子懸浮測試。文獻［5］提出一種單繞組無軸承飛輪電機，并分析了徑向懸浮力動態電流補償方法。文獻［6］提出一種應用于飛輪儲能系統無軸承交流單極電機，并分析了懸浮力模型。但是，目前國內外對于無軸承電機在飛輪儲能系統的中的應用尚處于樣機設計階段，對于控制系統的研究還并不多見，而電動汽車內部環境復雜、突發狀況多、模型易失配，要求控制系統對電機參數變化以及不確定的外部干擾具有較強的魯棒抑制能力。

本文介紹了無軸承無刷直流電動機懸浮力產生的原理，并建立了數學模型;對傳統的內模控制進行改進，采用兩自由度的內模控制方法;并設計了轉矩子系統和懸浮力子系統的內模控制器，利用MATLAB/Siumlink 仿真平臺搭建仿真模型，并與傳統的PID 調節方式進行對比。最后，通過樣機試驗驗證了系統的有效性，轉子能夠在沒有機械接觸的情況下穩定懸浮。

1 徑向懸浮力產生的原理

如圖1 所示，無軸承無刷直流電動機由定子軛、定子齒、轉子鐵心、永磁體和轉軸組成，定子齒均勻分布在定子軛內表面，轉矩繞組和懸浮力繞組采用集中繞組的形式，同時疊繞在定子齒上。其中，三相轉矩繞組A 相、B 相和C 相分別由A1，A2，A3，A4線圈，B1，B2，B3，B4 線圈和C1，C2，C3，C4 線圈串聯構成。懸浮力繞組a1 和a2 構成a 套懸浮力繞組，b1 和b2 構成b 套懸浮力繞組，c1 和c2 構成c套懸浮力繞組，每套懸浮力繞組都能獨立產生xoy平面的內的任意懸浮力。永磁體以表貼式安裝在轉子表面，轉子鐵心套在轉軸上。

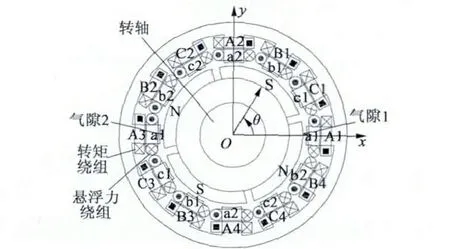
圖1 無軸承無刷直流電動機本體截面圖

無軸承無刷直流電動機懸浮力產生的原理主要是通過改變轉子周圍的氣隙磁密產生的。如圖1 所示，當轉子轉動到30°時，向a1 懸浮力繞組中通入如圖1 所示方向的電流，原有的氣隙磁密平衡被打破，使得氣隙1 處的磁通密度增加，氣隙2 處的磁通密度減小，產生沿著x 軸正方向的可控懸浮力;同理，當給懸浮力繞組a2 通電時也會使得轉子周圍的氣隙磁密不平衡，從而產生沿著y 軸方向的可控懸浮力，兩者合成就可以得到所需的懸浮力。所以，當我們對通入a 套懸浮力繞組中的電流的大小和方向進行調整時，就可以得到在xoy 平面內任意方向的可控懸浮力。圖2 是每套懸浮力繞組通電時產生的相位圖［7］。

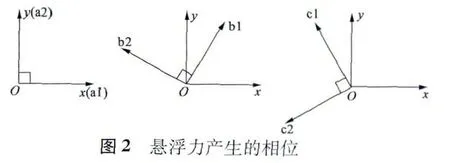
2 無軸承無刷直流電動機數學模型

2.1 轉矩子系統數學模型

在無軸承無刷直流電動機中，其轉矩子系統工作原理和數學模型與傳統的無刷直流電動機類似。其三相繞組的電壓方程:

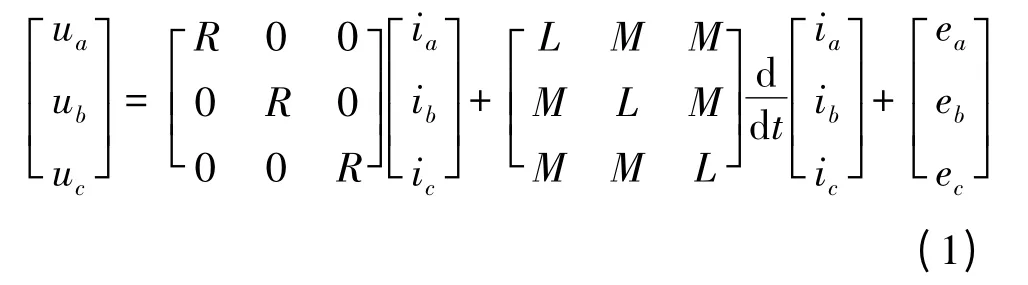
式中:ua，ub和uc為轉矩繞組相電壓;ia，ib和ic為轉矩繞組相電流;ea，eb和ec為轉矩繞組相電動勢;R為轉矩繞組電阻;L 為轉矩繞組自感;M 為轉矩繞組兩相間互感。

采用Y 型聯結時，ia+ib+ic=0，式(1)可簡化:

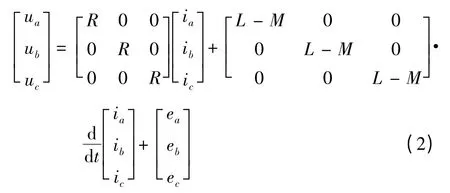
電磁轉矩方程式可表示:

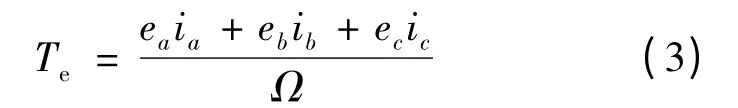
式中，Ω 是電機的機械角速度。

電壓平衡方程:

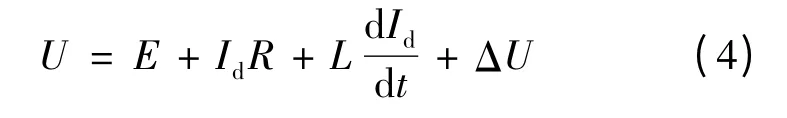
式中:U 是輸出電壓;E 是電樞繞組反電動勢;Id是電樞繞組電流;R 是電樞繞組電阻;ΔU 是功率開關管壓降。

2.2 懸浮力子系統數學模型

無軸承無刷直流電動機運行時，轉子主要受到兩種懸浮力。一種是由轉子偏心產生的不平衡磁拉力。當轉子未發生偏心時，轉子周圍磁密對稱分布，轉子受到的合力為零;當轉子發生偏心時，轉子周圍磁密不再平衡，所受合力不為零，即產生了沿著氣隙長度減小方向的不平衡磁拉力。第二種是懸浮力繞組通電產生的電磁力。因為轉子不再處于中心位置，所以需要給懸浮力繞組通電，產生電磁力以克服偏心產生的不平衡磁拉力，這樣才能使轉子的所受合力始終指向中心位置。不平衡磁拉力和電磁力相互作用，才能夠保持轉子的穩定懸浮［7］。

由于轉子偏心產生的不平衡磁拉力:

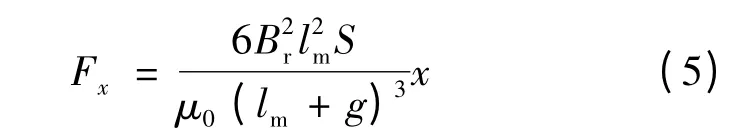
式中:lm為永磁體厚度;g 為平均氣隙長度;μ0為真空磁導率;S 為磁路的有效截面積;Br為剩磁密度。

懸浮力繞組a11通電時的電磁力:

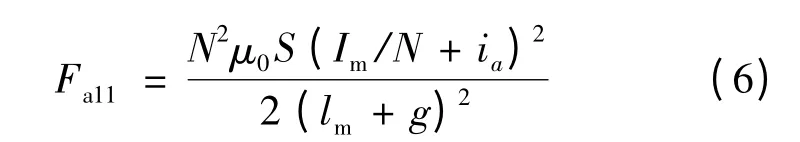
根據對電磁力Fa11的分析推導過程，可得懸浮力繞組a12通電時產生的電磁力:

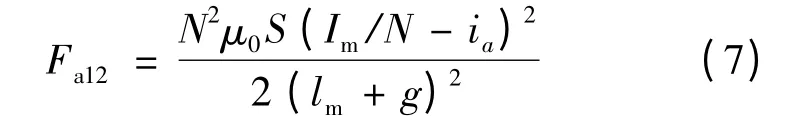
由式(6)、式(7)可得懸浮力繞組a1對轉子的電磁力合力:

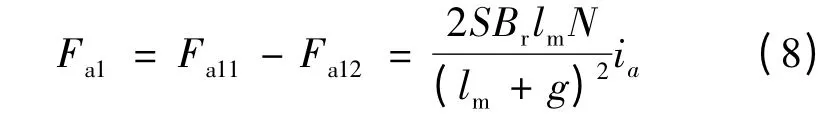
式中:N 為懸浮力繞組匝數;ia為懸浮力繞組通入的電流。

轉子沿著x 軸方向的合力為式(5)所示的不平衡磁拉力和式(8)所示的懸浮力共同作用形成，可以表示:

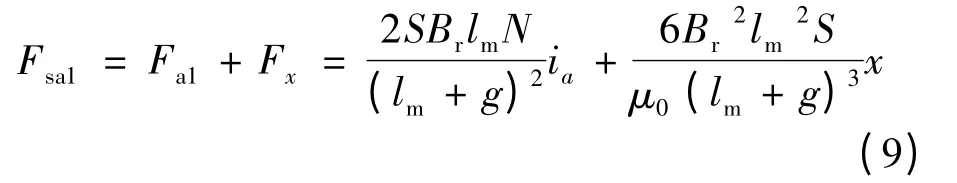
設轉子質量m，不考慮外加干擾力分量(主要為轉子重力)，則無軸承無刷直流電動機運動方程:

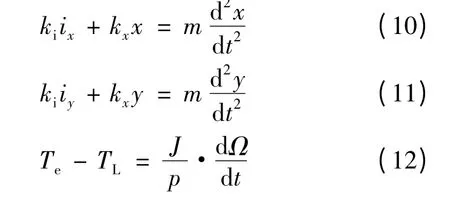
3 無軸承無刷直流電動機內模控制器設計

3.1 內模控制

內模控制是一種以過程數學模型為基礎進行控制器設計的先進控制策略，與傳統的反饋控制相比，其優點是具有更好的動態響應能力且能兼顧穩定性。

控制系統的抗擾性和跟隨性是衡量交流調速系統的的兩大重要技術指標。傳統結構的單自由度內模控制器在參數設計時需要對跟隨性和抗擾性進行平衡，在參數調節上增加了難度。圖3 是一種兩自由度內模控制結構，其中，Gp(s)為被控對象;Gm(s)為數學模型(s)為內模控制器;(s)為前饋控制器;R(s)，U(s)和Y(s)分別為參考輸入、控制輸出和系統輸出;d(s)為外部干擾。(s)調整系統的抗擾性，(s)調整系統的跟隨性［8］。

3.2 轉速子系統內模控制器設計

轉速子系統部分與傳統的無刷直流電動機類似，傳統的無刷直流電動機一般采用雙閉環調速系統，對其建模可以得到無刷直流電動機雙閉環調速系統的動態結構圖，如圖4 所示。［9］。

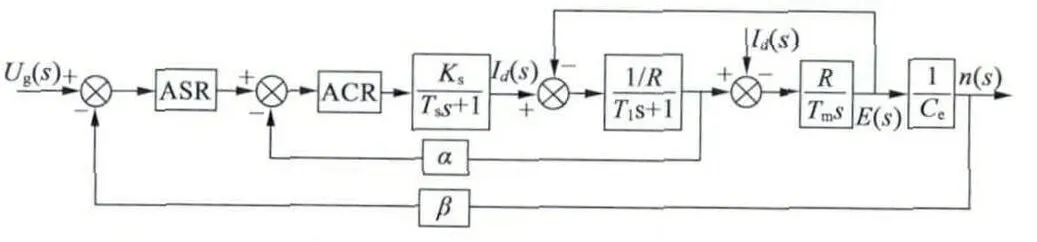
圖4 無刷直流電動機雙閉環調速系統動態結構圖

從圖4 中可以看出，在電流環內存在反電動勢的產生的交叉反饋，這意味著轉速環輸出量對電流環有一定的影響。但是在實際過程中，電流環的調節過程比轉速變化和反電動勢變化要快得多。即當電流調節過程結束時，反電勢只有很小的變化，因此在電流調節器快速調節過程中，可以認為反電勢E基本不變。則可以對電流環做簡化處理，得到如圖5 所示的電流環簡化結構圖。

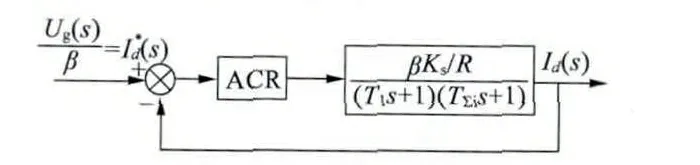
圖5 電流環簡化結構圖

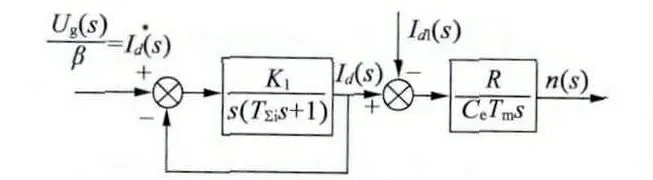
圖6 動態結構簡化圖

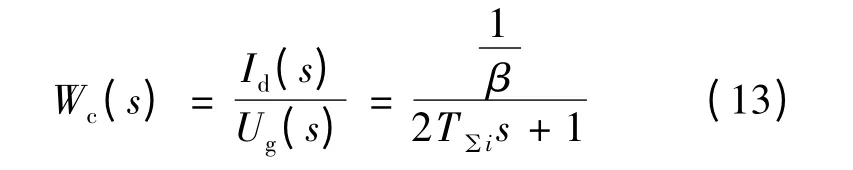
將簡化后的動態結構圖與兩自由度內模控制相結合可以到如圖7 所示的無刷直流電動機內模控制系統框圖。

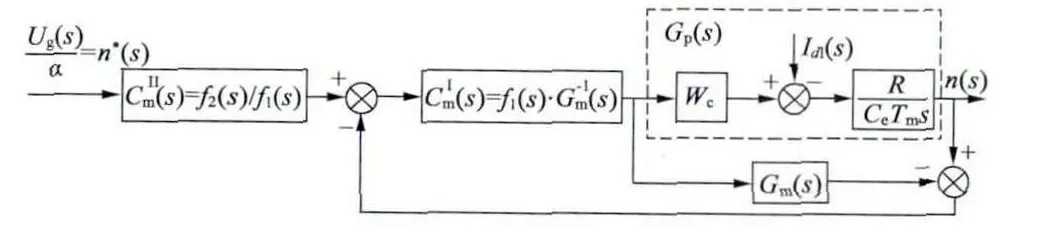
圖7 無刷直流電動機內模控制系統框圖

設計低通濾波器:

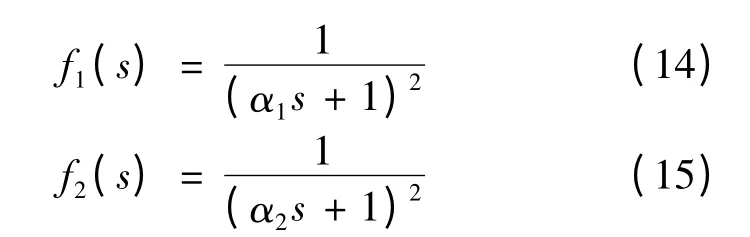
則對應的內模控制器和前饋控制器分別:

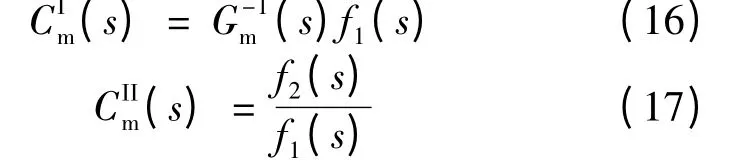
3.3 懸浮力子系統內模控制器設計

根據式(10)、式(11)的轉子運動方程，在忽略外部干擾的情況下，可以得到懸浮力子系統的傳遞函數:

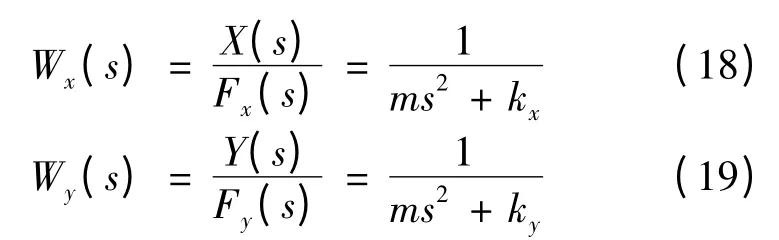
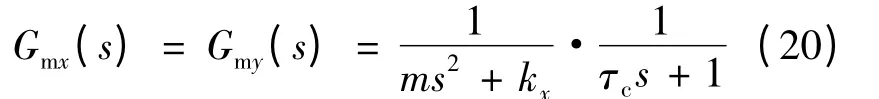
則設計x 軸內模控制器及前饋控制器:

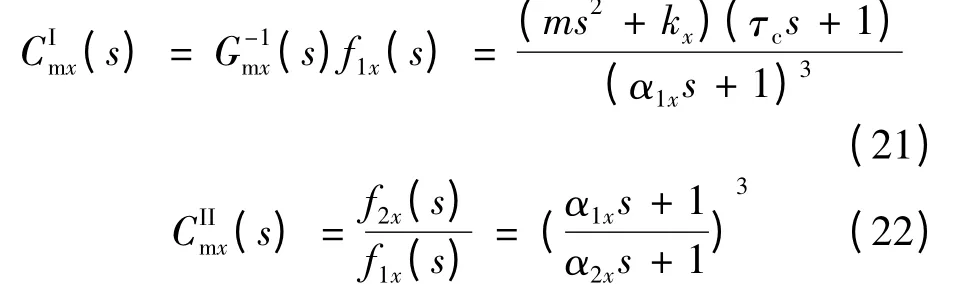
同理，y 軸內模控制器及前饋控制器:

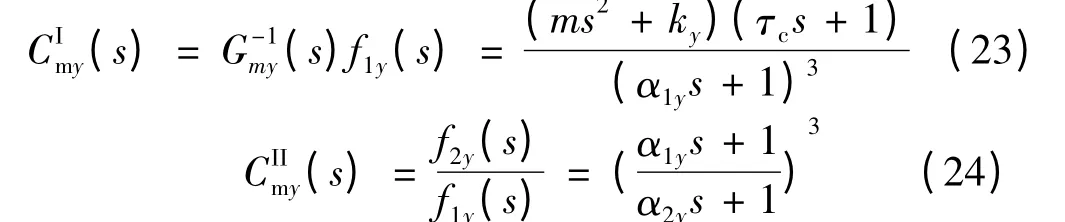
無軸承無刷直流電動機控制系統結構框圖如圖8 所示。

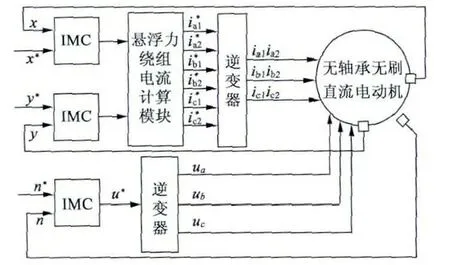
圖8 無軸承無刷直流電動機控制系統結構框圖

4 仿真結果及試驗

為了驗證所設計的內模控制系統的有效性，利用MATLAB/Simulink 工具箱搭建控制系統仿真模型，進行仿真實驗。仿真結果顯示，圖9 為電機轉速階躍響應曲線，電機給定轉速為1 500 r/min，在0.4 s時下降到1 000 r/min，實行減速運行。由圖9 可知，電機轉速響應較快，轉速幾乎無超調，能迅速達到額定轉速(小于0.1 s)，在0.4 s 突加負載，轉速發生階躍變化時，跟蹤時間短，系統的抗擾性和跟隨性良好。圖10 為轉矩響應曲線，電機起動轉矩大，保證了電機能夠在很短時間內達到額定轉速，由于摩擦轉矩的影響，電機的空載轉矩不為零，在0.4 s 負載突變時，電機的轉矩也隨之階躍變化。

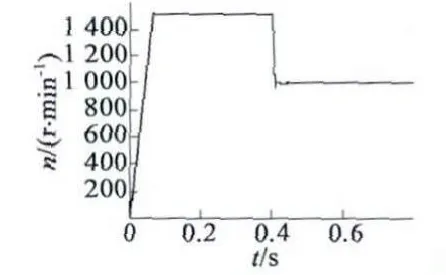
圖9 電機轉速響應曲線

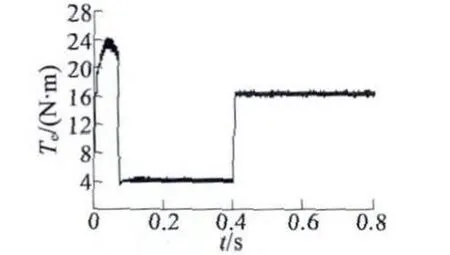
圖10 電機轉矩響應曲線

圖11(a)和圖11(c)分別為使用所設計的內模控制系統和傳統PID 控制系統下x 軸徑向位移階躍響應曲線;圖11(b)和圖11(d)為使用上述兩種控制系統下y 軸徑向位移階躍響應曲線。從圖11 中可以看出，使用內模控制系統的徑向位移響應曲線比使用PID 控制系統的徑向位移響應曲線更加平穩，位移發生突變時幾乎無超調。當x 軸方向位移給定突變時或y 方向位移給定突變時，徑向位移之間并沒有相互影響，驗證了徑向力之間的動態解耦效果。且當在0.4 s 突加負載和轉速發生變化時，x軸方向和y 軸方向位移也不受影響，系統的轉速和徑向力之間實現了動態解耦，保證了無軸承無刷直流電動機的穩定運行。

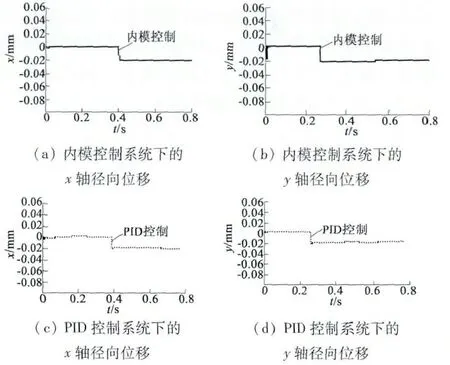
圖11 兩種控制系統下的徑向位移響應曲線

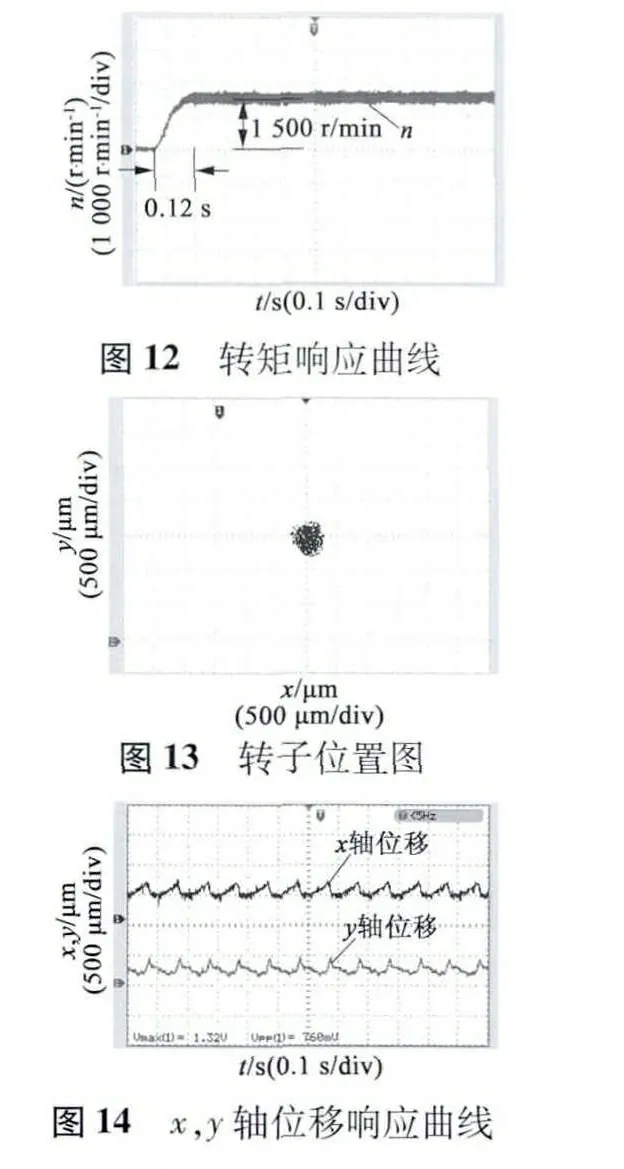
最后通過樣機進行試驗，樣機本體為無軸承無刷直流電動機，采用TMS320F2812 DSP 進行控制。試驗結果如下，圖12 是轉矩響應曲線，從圖12 中可以看出，轉矩響應時間為0. 12 s，到達額定轉速1 500 r/min，轉速相對比較平穩。圖13 是轉速穩定后的轉子位置圖，可見，轉子能夠懸浮于中心。圖14 是轉速穩定后x，y 軸的位移響應曲線，從圖中可見，x，y 軸的位移波動大約在200 μm 左右，波動不是很大，并且與圖13 相一致。由此可見，電機能夠穩定運行，并且能夠實現懸浮，懸浮性相對良好。

5 結 語

無軸承無刷直流電動機是一種新型的高性能電機，作為飛輪儲能系統的驅動電機具有潛在的應用價值。本文針對電動汽車中飛輪儲能系統運行環境復雜、狀況多變等情況，提出使用內模控制系統控制無軸承無刷直流電動機，以提高系統的跟隨性和魯棒性。本文介紹了無軸承無刷直流電動機徑向懸浮力產生的原理，并構建了數學模型。根據數學模型并結合兩自由度內模控制系統，分別設計轉速子系統和懸浮力子系統的內模控制器。通過仿真結果我們可以看出，相比于經典PID 控制系統，內模控制系統具有更加優越的抗干擾性能，為系統的全局穩定性提供了保障，使系統具有更好的跟隨性和魯棒性。最后，樣機試驗實現了轉子的穩定懸浮，驗證了系統的有效性。

［1］ 張邦力，胡漢春，何青，等. 飛輪儲能裝置儲能狀態控制研究［J］.機電產品開發與創新，2010，23(6):100－102.

［2］ 劉奕辰，朱熀秋. 無軸承無刷直流電機研究現狀及發展趨勢［J］.微電機，2014，47(8):74－78.

［3］ OOSHIMA M，KITAZAWA S，CHIBA A，et al.Design and analyses of a coreless－stator－type bearingless motor/generator for clean energy generation and storage systems［J］. IEEE Transactions on Magnetics，2006，42(10):3461－3463.

［4］ OOSHIMA M，KOBAYASHI S，TANAKA H. Magnetic suspension performance of a bearingless motor/generator for flywheel energy storage systems［C］//IEEE Power and Energy Society General Meeting，2010:1－4.

［5］ YUAN Y，SUN Y，HUANG Y.Radial force dynamic current compensation method of single winding bearingless flywheel motor［J］.IET Power Electronics，2015，8(7):1224－1229.

［6］ SEVERSON E，NILSSEN R，UNEDLAND T，et al. Suspension force model for bearingless AC homopolar machines designed for flywheel energy storage［C］//2013 7th IEEE，GCC Conference and Exhibition，2013:274－279.

［7］ 陳雷剛，朱熀秋.無軸承無刷直流電機徑向懸浮力精確數學模型［J］.中國電機工程學報，2012，32(36):75－81.

［8］ 周志超.永磁無刷直流電機控制及其在變槳距系統中的應用研究［D］.成都:西南交通大學，2010.

［9］ 李志坤，讓余奇.基于內模控制的直流無刷電機調速系統設計［J］.艦船電子工程，2009，29(2):188－191.