超混沌系統的反同步研究

李賢麗 張超穎 竇雪瑩

(東北石油大學，黑龍江 大慶 163318)

混沌運動是發生在確定的非線性系統中的一種隨機行為，其對初始條件高度敏感，具有復雜的動力學性質，且難以預測，目前廣泛地應用于物理學、地質學、生物學、化學及保密通信[1]等工程領域中。混沌在發現之初是用來解釋某些自然和物理現象的，如蝴蝶效應及天氣預報等。近年來，人們開始控制和應用混沌，混沌控制的主要方法有線性反饋法[2]、周期擾動與激勵控制[3]、參數擾動法。基于混沌控制的方法，在一定條件下，構造出四維自治超混沌系統，超混沌系統與混沌系統相比具有更為復雜的動力學行為，它具有兩個或兩個以上正的李雅普諾夫指數，拓撲結構更為復雜，動態行為更加難以預測，更難被破解。將超混沌同步技術應用于保密通信系統時，有著更強的保密性能。混沌信號應用于保密通信是要把有用信號隱藏在混沌信號里，再在接收端提取出有用信號，可以直接利用混沌通信，也可以利用混沌同步實現通信，所以對超混沌同步方法的研究也極為重要。混沌同步是混沌控制的一種特殊形式，混沌系統的同步類型有完全同步、投影同步、反同步[4,5]及相同步[6]等，混沌同步方法有自適應同步法[7]、反饋同步法[8]、基于狀態觀測器廣義投影同步法[9]和脈沖同步法[10]。

筆者針對超混沌liu系統，采用基于狀態觀測器法和反饋法設計合適的觀測器和控制器，從理論分析和數值計算兩個角度出發，研究超混沌系統在不同初始值條件下的反同步問題。同時，通過同步曲線和誤差曲線，比較兩種方法的不同之處。

1 基于狀態觀測器法實現反同步①

超混沌系統具有兩個正的李雅普諾夫指數，與三維混沌系統相比具有更加復雜的拓撲結構，所以其動力學性質也更為復雜。筆者選取一個超混沌liu系統[11]，其系統方程為：

(1)

其中，a=35，b=35，m=2，c=2，d=10。

首先，采用基于狀態觀測器的方法來實現liu系統自身的反同步。把系統(1)作為驅動系統并化為f(x)=Ax+Bg(x)+G的形式。驅動系統為：

(2)

其中，A、B、G、D為定常矩陣：

G=0

根據狀態觀測器理論，響應系統可表示為：

(3)

響應系統中的α為投影同步中的比例系數，為了使A-BD的特征值為負實部，取特征值為(-0.5，-1，-1.5，-2)，運用極點配置法得到矩陣D：

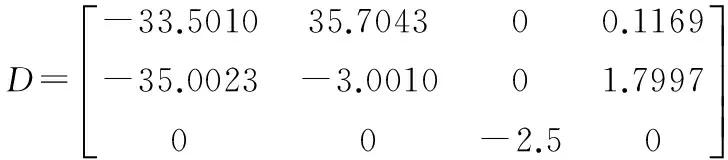
此時的響應系統為：

(4)

所謂反同步就是指混沌系統運動軌道的振幅大小相等、方向相反。因此，令比例系數α=-1，系統(1)的初始值為(2，20，35，-2)，系統(3)的初始值為(12，30，50，40)，利用Matlab進行數值仿真得到結果，此時驅動系統(1)和響應系統(3)實現了反同步，其系統的反同步曲線和反同步誤差如圖1、2所示。由圖2可知，系統的誤差e1、e2、e3、e4隨著時間的增加逐漸趨于零點，也就是驅動系統和響應系統達到了反同步。

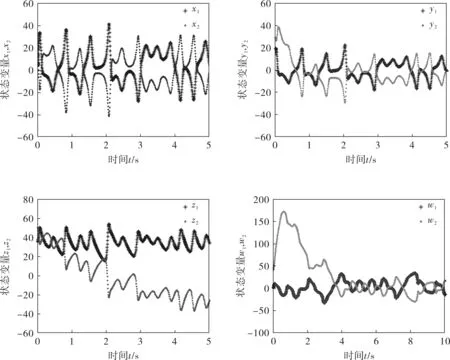
圖1 驅動-響應系統中的各狀態變量的反同步曲線

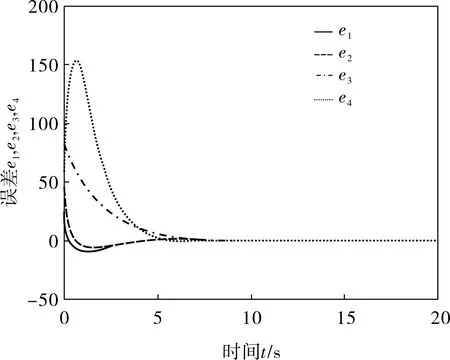
圖2 驅動-響應系統的反同步誤差曲線

2 反饋法實現反同步

同樣選取系統(1)作為驅動系統，那么，其同結構加了控制器后的響應系統為：

(5)

其實U=(u1,u2,u3,u4)T即將要設計的控制器。

將系統(1)和系統(5)相加，得到誤差動態系統為：

(6)

其中e1=x1+x2，e2=y1+y2，e3=z1+z2，e4=w1+w2，設計合適的控制器U=(u1,u2,u3,u4)T，將驅動系統(1)和響應系統(5)實現反同步。

以非線性控制理論為依據，設計控制器U為：

(7)

由式(6)、(7)可將誤差系統轉化為如下形式：

(8)

取李雅普諾夫函數為：

(9)

對式(9)取導數為：

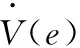
=e1[a(e2-e1)+μ1]+e2(be1-me4+μ2)+

e3(-ce3+μ3)+e4(de2+μ4)

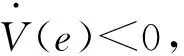
(10)

則可得：

令驅動系統(1)的初始值為(2，20，35，-2)，響應系統(5)的初始值為(12，30，50，40)，運用四階Runge-Kutta法在Matlab中進行數值仿真，從而得到系統的反同步曲線和反同步誤差曲線如圖3、4所示。

由圖2可知，當t=12.8s時，基于狀態觀測器法得到的同步誤差曲線趨于零點。由圖4可知，當t=3.0s時，反饋法得到的誤差曲線趨于零點，由此可知，對于一般系統而言，采用反饋法來實現系統的同步，雖然控制器設計復雜，但是同步速度較快。

3 結束語

根據狀態觀測器理論和李雅普諾夫定理，采用基于狀態觀測器法和反饋法分別設計了觀測器和控制器，對liu系統的反同步進行了理論論證，同時，利用Matlab對該系統進行數值模擬得到了系統的反同步曲線和反同步誤差曲線，驗證了兩種方法的可行性和有效性。基于狀態觀測器的方法具有算法簡單、計算量小的優點，與其相比，通過反饋法實現的系統同步，雖然控制器的設計較為復雜，但其同步速度相對較快，更適用于保密通信。

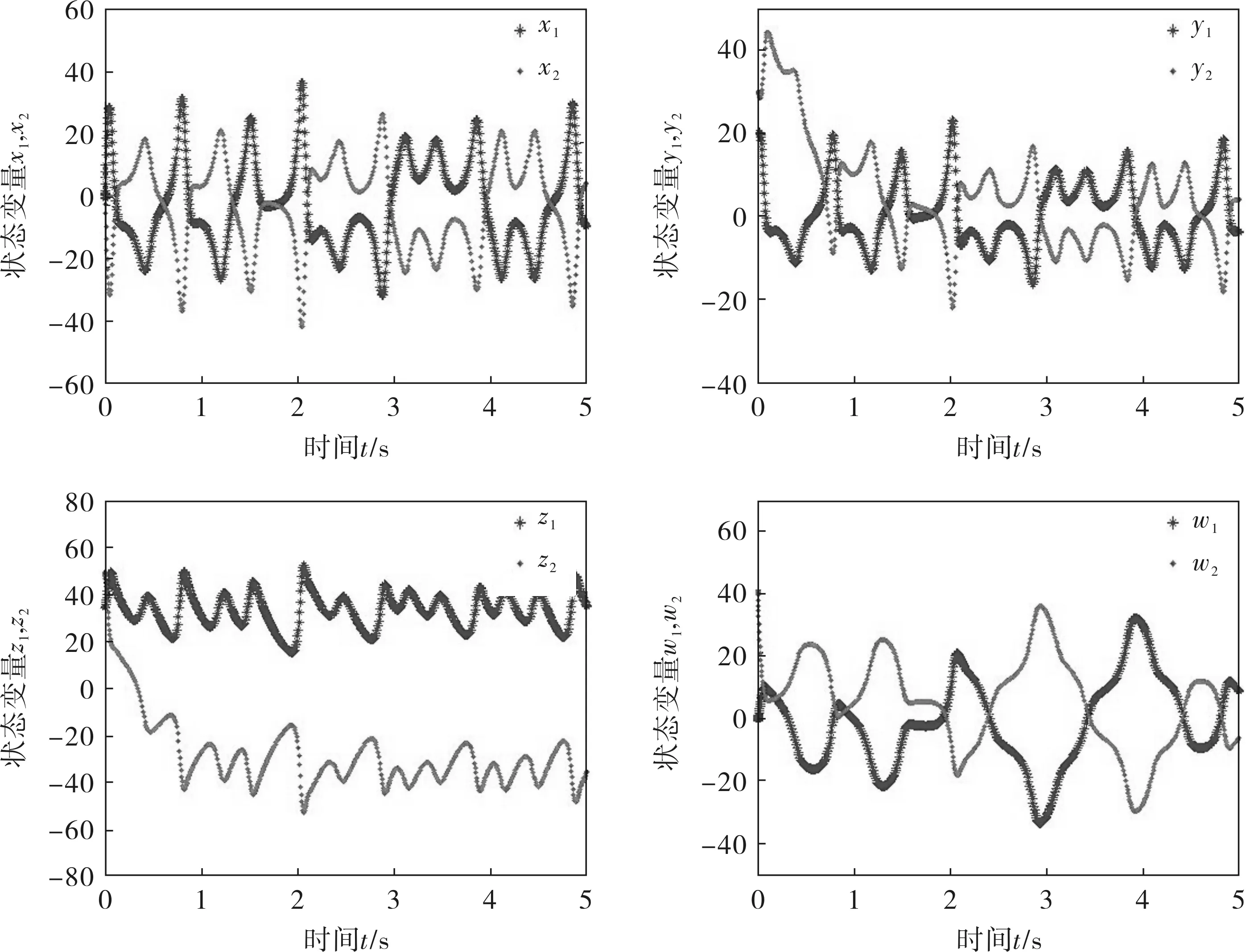
圖3 驅動-響應系統中的各狀態變量的反同步曲線

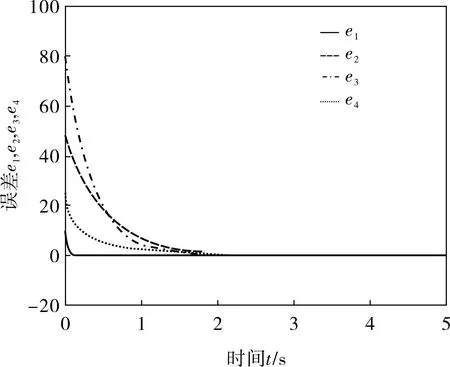
圖4 系統的反同步誤差曲線

[1] 李瑞紅,陳為勝,李爽.超混沌Lorenz系統的投影同步及其在保密通信中的應用[J].電路與系統學報,2011,16(2):41～45.

[2] 李賢麗,王升,張秀龍,等.四翼混沌吸引子系統控制[J].大慶石油學院學報,2011,35(4):117～122，14.

[3] 李賢麗,張笑宇,王升，等.Lorenz超混沌系統的周期擾動與激勵控制[J].大慶石油學院學報,2010,34(4):105～109，131.

[4] Chen J Y,Wong K W,Cheng L M,et al. A Secure Communication Scheme Based on the Phase Synchronization of Chaotic Systems[J].CHAOS,2003,13(2):508～514.

[5] 王興元.混沌系統的同步及在保密通信中的應用[M].北京：科學出版社,2012.

[6] Tam W M,Lau F C M,Tse C K.Analysis of Bit Error rates for Multiple Access CSK and DCSK Communication Systems[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2003,50(5):702～707.

[7] 單梁,劉光杰,李軍,等.Liu混沌系統的線性反饋和狀態觀測器同步[J].系統仿真學報,2007,19(6):1335～1338.

[8] Hu M F,Xu Z Y,Zhang R,et al.Adaptive Full State Hybrid Projective Synchronization of Chaotic Systems with the Same and Different Order[J].Physics Letters A, 2007,365(4):315～327.

[9] Zhang G, Liu Z R,Ma Z J.Generalized Synchronization of Different Dimensional Chaotic Dynamical Systems[J].Chaos,Solitons and Fractals,2007,32(2):773～779.

[10] 馬鐵東,江偉波,浮潔.基于比較系統方法的分數階混沌系統脈沖同步控制[J].物理學報,2012,61(9)：39～44.

[11] 高智中,王穎.一個新超混沌系統及其線性反饋控制[J].數值計算與計算機應用,2012,33(3):167～172.