基于PSO-LS-SVM的主蒸汽流量測量

周云龍 王 迪

(東北電力大學，吉林 吉林 132012)

火電機組主蒸汽流量的測量，對于機組經濟性能分析和節能降耗有著重要的意義。目前，對于主蒸汽流量的測量，主要有直接測量法和間接測量法兩種。直接測量法通常采用流量噴嘴(或孔板)方案，這種方法簡單、準確，但是會造成節流損失，對于大型火電機組而言，該過程損失是不可忽略的[1]。因此，目前對于主蒸汽流量的測量主要是采用基于機理建模的方法，依據反映汽輪機通流部分工作特性的費留格爾公式，但由于費留格爾公式的適用范圍，使用調節級后相關壓力參數需進行多次修正，計算過程較為復雜，并存在較大的誤差，容易影響機組其他參數的監測[2～4]。所以，利用相關參數建立一種簡單、準確并且不會對機組經濟性能產生影響的主蒸汽流量數學模型意義重大。

隨著人工智能的發展，火電機組參數軟測量技術日漸成熟，神經網絡[5]及支持向量機[6]等開始應用于主蒸汽流量的測量。統計學習理論是由Vapnik V建立的一種專門研究小樣本情況下機器學習規律的理論，支持向量機是在這一理論基礎上發展而來的一種新的學習方法，支持向量機能夠較好地解決小樣本、非線性、高維數和局部極小點的實際問題，在火電機組參數監測方面已有重要應用[7]。Suykens J A K和Vandewalle J提出最小二乘支持向量機方法(Least Squares Support Vector Machines,LS-SVM)，采用最小二乘線性系統作為損失函數，將求解過程變成線性方程組求解，求解速度相對加快[8]。和其他算法一樣，其性能依舊依靠參數的選擇，如何選擇最優參數以提高LS-SVM的學習和泛化能力，對于主蒸汽流量的軟測量極為重要。

微粒群優化算法(PSO)是近年來發展很快的一種智能尋優算法，與遺傳算法和蟻群算法相比，具有簡單、快速、易行的特點。為了研究主蒸汽流量的測量，筆者提出利用PSO算法優化LS-SVM參數，從而建立主蒸汽流量的測量模型。

1 最小二乘支持向量機算法①

支持向量機的主要思想是通過事先選擇的非線性映射將輸入向量映射到高維特征空間，在這個空間中構造最優決策函數[9]。在構造最優決策函數時，利用風險最小化原則，并巧妙地利用原空間的核函數取代高維特征空間的點積運算。

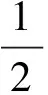
(1)

s.t.yi=φ(xi)·w+b+ξi，i=1，…，l

(2)

用拉格朗日法求解這個問題，即：

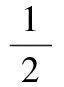
b+ξi-yi]

(3)

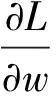
(4)

(5)

ai=cξi

(6)

w·φ(xi)+b+ξi-yi=0

(7)

定義核函數K(xi,xj)=φ(xi)·φ(xj)，K(xi,xj)是滿足Mecer條件的對數函數，所以優化問題轉化為求解線性方程：

首先，環境問題目前已經成為全球性問題，人類要想可持續發展，就一定要改變傳統的以犧牲資源和環境為代價殺雞取卵的發展方式。這就促進了節能技術在各個領域的應用。電氣自動化技術也產生了相應的節能技術研究領域，作為節能技術的重要組成部分，指導電氣自動化技術的健康發展。

從而得到非線性預測模型：

(8)

2 粒子群優化算法

最小二乘支持向量機算法作為預測模型，其正確性主要依賴于對正則化參數c和高斯核參數σ的選擇，這兩個參數決定了LS-SVM預測模型的學習能力和泛化能力。其中正則化參數主要用于控制函數的擬合誤差，正則化參數越大，擬合誤差越小，相應的訓練時間越長，但是過大會導致過擬合；高斯核參數越小，擬合誤差越小，訓練時間越長，若高斯核參數過小，也會導致過擬合。為了選擇最優的參數來建立預測模型，利用粒子群優化算法對參數進行優化。

粒子群優化算法是一種進化計算技術，最初由Kennedy J和Eberhart R提出[10]。PSO的基本思想是：將所優化問題的每一個解看作為一個微粒，每個微粒在n維搜索空間中以一定的速度飛行，通過適應度函數來衡量微粒的優劣，微粒根據自己和其他微粒的飛行經驗，來動態調整飛行速度，以期向群體中最好的微粒位置飛行，從而使所優化的問題得到最優解。

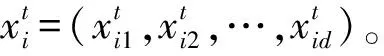
vij(t+1)=w·vij(t)+c1·r1·[pbestij(t)-xij(t)]+

c2·r2·[gbestj(t)-xij(t)]

(9)

xij(t+1)=xij(t)+vij(t+1)

(10)

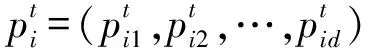
3 主蒸汽流量PSO-LS-SVM預測模型

3.1 PSO-LS-SVM預測模型的建立

按照式(9)、(10)更新粒子速度和位置，生成新一代種群。

根據設定的適應度函數，評價每個粒子的適應值，粒子的適應值越小，粒子的位置越好。其中，設定適應度函數為：

(11)

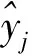
當計算終止后，將全局最優粒子映射為正則化函數和核函數，并以此為最優結果，從而得到LS-SVM預測模型。

利用建立好的預測模型對預測樣本進行預測。PSO-LS-SVM預測模型建立的流程如圖1所示。

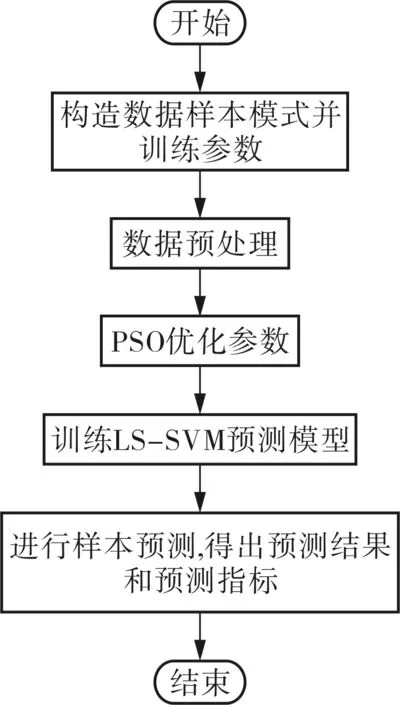
圖1 PSO-LS-SVM預測模型流程

3.2 模型特征變量的選取

主蒸汽流量實際是由進入汽輪機的流量與軸封門桿漏汽量、旁路蒸汽流量和扣除減溫水量得出的[11]，即：

G=Gq+Gl+Gp-Gj

(12)

式中G——主蒸汽流量；

Gj——各級減溫水流量；

Gl——軸封和門桿漏汽量；

Gp——旁路蒸汽流量；

Gq——進入主汽輪機蒸汽流量。

利用機理分析方法研究主蒸汽流量與相關機組運行參數之間的關系，筆者選擇機組負荷、主蒸汽壓力、主蒸汽溫度、各級減溫水流量、一段抽汽壓力、再熱器壓力和溫度、給水流量作為模型的輸入變量。訓練樣本的選取同樣是影響模型性能的重要因素，過少的訓練樣本無法滿足訓練要求，而過多的訓練樣本會導致訓練過擬合,影響網絡泛化能力。通常對訓練樣本的選取采用以下原則：樣本數據選取機組穩定運行工況下的典型數據；樣本數量的選取應與所構建的網絡特點對樣本數量的要求相適應。

筆者選取某330MW機組在65%～95%額定負荷工況的35組運行參數，其中均勻選擇其中30組數據作為訓練樣本，另外5組作為測試樣本。訓練樣本輸出擬合曲線如圖2所示，測試結果見表1，最大相對誤差為0.007 5。

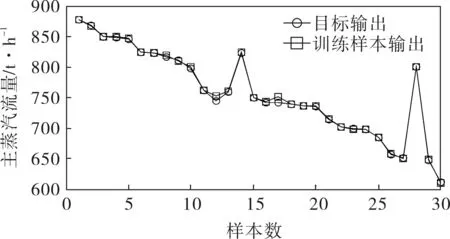
圖2 訓練樣本輸出擬合曲線

表1 PSO-LS-SVM預測結果

由圖2可知，采用PSO-LS-SVM算法對訓練樣本進行訓練，得到的結果能夠較好地反映期望值，證明該算法的正確性。由表1可知，利用該算法對測試樣本進行預測，計算結果能夠很好地反映出工程實際值，最大相對誤差在工程應用允許的范圍內。

為了研究粒子群算法的優化過程，在設定步數范圍內得出適應度隨優化步數的變化，變化曲線如圖3所示。通過觀察發現，適應度函數在約第125代時值最小，適應度為10.52。

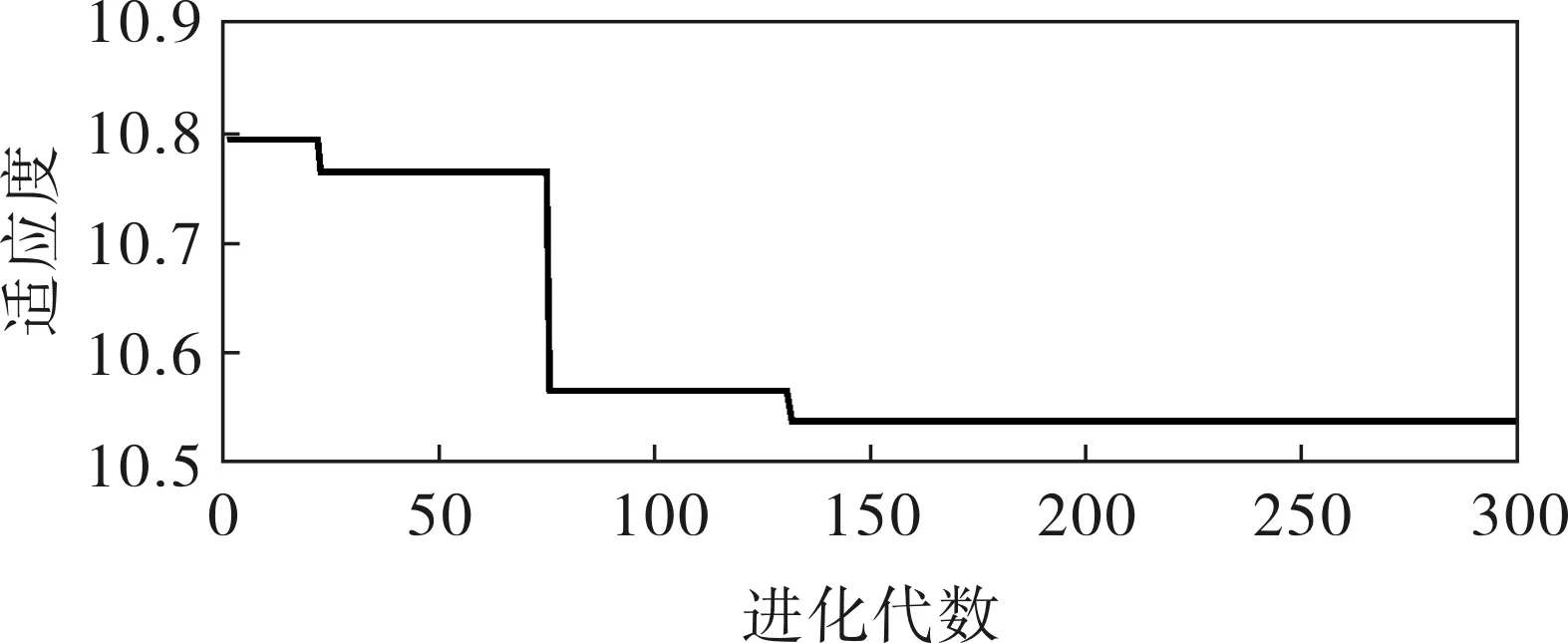
圖3 適應度隨進化過程的變化

4 結束語

利用粒子群優化算法優化最小二乘支持向量機的參數，以火電機組主蒸汽流量機理為基礎，選擇預測模型的特征變量，建立火電機組主蒸汽流量的預測模型，利用模型對參數預測值進行仿真研究，預測結果表明，利用粒子群算法優化最小二乘支持向量機參數的建模方法，能夠提高主蒸汽流量的預測精度，具有一定的工程實際應用性。

[1] 馮偉忠.大機組主蒸汽流量測量芻議[J].華東電力，2000，28(12)：14～17.

[2] 劉吉臻，閆姝，曾德良，等.主蒸汽流量的測量模型研究[J].動力工程學報，2011，31(10)：734～737.

[3] 李忠良.蒸汽流量測量的準確性分析[J].熱力發電，2009，38(3)：88～90.

[4] 李勇，王建君，曹麗華.汽輪機主蒸汽流量測量在線監測方法研究[J].熱力發電，2011，40(4):33～36.

[5] 王建星，付忠廣，靳濤，等.基于廣義回歸神經網絡的機組主蒸汽流量測定[J].動力工程學報，2012，32(2)：130～134.

[6] 王雷，張瑞青，肖增弘，等.基于SVM的主蒸汽流量回歸估計[J].華東電力，2008，36(12)：89～92.

[7] Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer,2005.

[8] Suykens J A K，Vandewalle J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3):293～300.

[9] 劉瑞蘭，牟盛靜，蘇宏業，等.基于支持向量機和粒子群算法的軟測量建模[J].控制理論與應用，2006，23(6)：895～899.

[10] Kennedy J,Eberhart R.Particle Swarm Optimization[C].Proc of IEEE International Conference on Neural Networks.Perth Australia：IEEE，1995:1942～1948.

[11] 趙晶睛，林中達.電廠主蒸汽流量測量與計算方法分析比較[J].燃氣輪機技術，2007，20(4)：39～42.