風力發電機組恒功率無模型自適應變槳距控制

姜 萍 趙振家

(河北大學 a. 電子信息工程學院；b. 羅克韋爾自動化實驗室，河北 保定 071000)

我國始終把可持續發展作為基本戰略路線，隨著近年煤炭及石油等常規能源的全面緊張，可再生能源的發展已是大勢所趨。我國風能資源豐富、且其成本相比其他可再生能源較低，在可再生能源中最具商業化和產業化發展前景。

近幾年來，變槳距風力發電機逐漸代替定槳距風力發電機成為主流機型。當風速達到額定風速以上時，變槳距風力發電機組可通過改變槳距角實現棄風，保持額定功率，實現功率的穩定。現如今大部分變槳距風力發電機組都采用PID算法，該算法簡單、易實現，但對于風力發電機組非線性、強耦合的特性，無法更好地維持功率恒定，因此如何改進算法，改善風力發電機組的控制性能，成為研究變槳距風力發電機的熱點之一。

羅秋濱等分析了無模型控制的抗干擾能力，克服了PID控制無法對非線性、強耦合系統實現穩定控制的弱點，并通過與PID調節器的抗干擾能力的仿真比較，進一步說明了無模型控制方法具有很強的抗干擾能力，對多變量強耦合系統進行控制可收到良好的效果[1～3]。曹榮敏和侯忠生利用Matlab軟件進行仿真實驗，證明了無模型方法對電機這種具有不確知動態非線性系統的有效性和穩定性[4]。金尚泰等將無模型自適應控制算法應用到永磁直線電機的速度控制中，控制器的設計僅需系統的輸入、輸出數據，并能夠實現參數適應性控制和結構自適應控制，仿真結果驗證了無模型自適應算法的有效性[5]。秦生升等基于微分幾何反饋線性化方法，提出變槳距風力發電機組恒功率控制策略，并將精確反饋線性化與H∞控制理論相結合設計了非線性H∞控制器，將其運用在風電變槳距控制中，在風速高于額定風速時調節風力機維持額定轉速[6，7]。張純明等根據模型參考自適應控制原理，以大型風力發電機組直流電動變槳距控制系統為研究對象，設計了一個高性能電動變槳距控制系統，并用李雅普諾夫穩定性分析給出自適應系統控制律[8]，仿真表明所設計系統有很好的跟蹤和伺服性。筆者基于無模型理論，設計了無模型自適應控制器，并將其運用在風電系統的變槳距控制中。

1 風力發電機組模型①

風力發電系統主要由風力機、齒輪傳動和發電機構成，其運行特性和控制策略與所用發電機類型和風力機特性密切相關。當風速從接近零上升到切入風速時，風力機經過齒輪傳動帶動發電機進行發電。根據不同的風況，風力發電系統的運行可以分為啟動區、最大風能追蹤區、恒轉速區和恒功率區[9]。

1.1 風力機模型

風輪是一種能截獲流動空氣所具有的動能，并將風輪葉片迎風掃掠面積內的一部分動能轉化為有用機械能的裝置圈。

由空氣動力模型可知，風力機吸收的機械功率為：

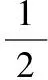
(1)

風力機的運動方程為：

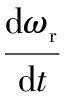
(2)

風力機轉矩與功率的關系為：

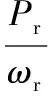
(3)

式中Cp(λ，β)——風能利用系數；

Jr——轉動慣量；

Pr——風力機捕獲的機械能；

R——風輪半徑；

V——風速；

β——槳距角；

ρ——空氣密度。

Cp(λ，β)的表達式為：

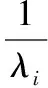
(4)

風輪所捕獲的風能與風速是3次方的非線性關系，Cp(λ，β)又具有λ，β的非線性特性，風力機的轉矩和功率之間又存在著某種耦合，因此風力機是一個非線性、強耦合的系統。

1.2 齒輪傳動模型

根據風輪氣動特性，風輪產生的轉矩Tr作用在帶有轉動慣量Jg的風輪上。風輪通過增速比為n的增速器連接到轉動慣量Jg的發電機上，發電機將產生反轉矩Te，得到傳動系統的質量塊模型：

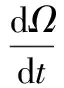
(5)

其中，k為常數。

1.3 異步電機模型

異步電機的運動方程為:

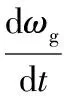
(6)

式中Jg——發電機的轉動慣量；

Te——發電機上的反扭矩；

Tm——高速軸上的扭矩；

ωg——發電機的機械角速度。

異步電機的電磁轉矩為[10]：

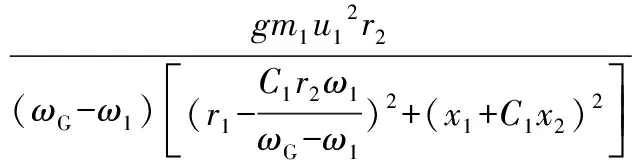
(7)

式中C1——修正系數；

g——發電機極對數；

m1——相數；

r1、r2——分別為定子和歸算后轉子繞組的電阻；

x1、x2——分別為定子和歸算后轉子繞組的漏抗；

u1——電網電壓；

ω1——同步轉速；

ωG——發電機的當量轉速。

異步發電機的功率需要去除不確定的銅損耗和鐵損耗，并且轉矩又與電壓、角速度存在非線性、強耦合關系，所以異步電機也是一個非線性、強耦合的系統。

綜上，風力發電機組中存在大量非線性、強耦合環節，傳統的PID調節已經不能滿足生產實際的要求，因此需要尋找更優的控制策略以對非線性、強耦合系統實現更好的調節。

2 變槳距原理

風機上的槳距角指的是葉片頂端翼型弦線與旋轉平面的夾角。調節槳距角的目的主要有：在啟動時獲得比較大的氣動扭矩，使葉輪克服驅動系統的空載阻力矩；在額定風速后，限制功率輸出，使功率平穩，保護機械和電路系統，同時降低載荷；剎車時，提供很大的氣動阻力，使葉輪的轉速快速降低，避免機械剎車造成慣性力太大而造成的傷害。

根據不同的風況，風力發電系統的運行可以分為啟動區、最大風能追蹤區、恒轉速區和恒功率區。在啟動區內，風速大于或等于切入風速時發電機并網發電；在最大風能捕獲區風力機組并網運行在最高轉速以下，風力機槳距角處于不調節的定槳運行狀態；在恒轉速區風力發電機組已達到最高轉速，但風力機的輸出功率尚未達到額定輸出狀態，為保護機組不過載，不再進行最大風能追蹤運行，而是通過風力機子系統的變槳距控制來調節槳距角，確保在允許最大轉速上的恒轉速發電運行；在恒功率區，隨著風速的增大風力機輸出機械功率不斷增大，發電機達到其功率上限。

2.1 風力發電機組功率和槳距角的關系

風力發電機組的功率和槳距角的關系可以近似表示為：

P(t+1)=f(P(t),P(t-1),…,P(t-ny),β(t),

β(t-1),…,β(t-nu))

(8)

2.2 控制律的計算

引入準則函數[11]：

J(β(k))=[|P*(k+1)-P(k+1)|2+

λ|β(k)-β(k-1)|2]

(9)

對β(k)求導并令其等于零，解得：

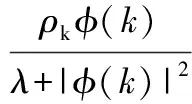
(10)

其中ρk是步長序列，λ是權重因子。控制律算法中λ的作用有兩個：其一是限制了Δβ(k)的變化，因此可以間接限制偽偏導數值量的變化；其二是可避免控制律算法中分母可能出現為零的這種奇異情況。從控制律算法可以看出，此類控制律與受控系統數學的模型結構和系統階數無關。

2.3 偽偏導數的計算

引入準則函數：

J(φ(k))=[(P*(k)-P(k-1)-φ(k)Δβ(k-1))2+

μ(φ(k)-φ(k-1))2]

(11)

進行與上述相類似的極小化程序，可以得到偽偏導數估計算法：

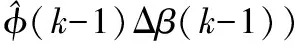
(12)

其中μ是權重因子，ηk是步長。

3 控制器的設計

由上述可以得到該系統不依賴于受控系統數學模型的無模型自適應方案[12]，即：

Δβ(k-1))

(13)

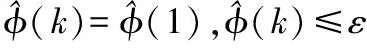
(14)

|Δβ(k-1)|≤ε

(15)

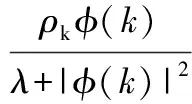
(16)

其中ηk，ρk∈(0，1]；μ，λ是權重因子；ε是一個充分小的數；φ(1)是φ(k)的初值。

筆者基于Matlab設計控制器，并將其在風力發電機組中進行仿真，當風速高于額定風速時，由實際功率和額定功率的偏差分別經過PID和無模型自適應(MFA)控制器進行調節。系統的結構框如圖1所示。

圖1 無模型自適應變槳距原理框圖

4 仿真分析

筆者基于Matlab/simulink對 3臺3MW風力發電機組進行了仿真實驗。定子的電阻為0.004 843(pu)，電感為0.124 8(pu)；轉子的電阻為0.004 377(pu)，電感為0.179 11(pu)，互感為6.77(pu)，極對數為3，轉動慣量為5.04(pu)，額定風速為9m/s。無模型控制器的參數λ=0.3，μ=0.8；PID控制器的參數kp=5，ki=25。當風速為階躍風速時，所得發電機功率和風力機轉速曲線如圖2、3所示。

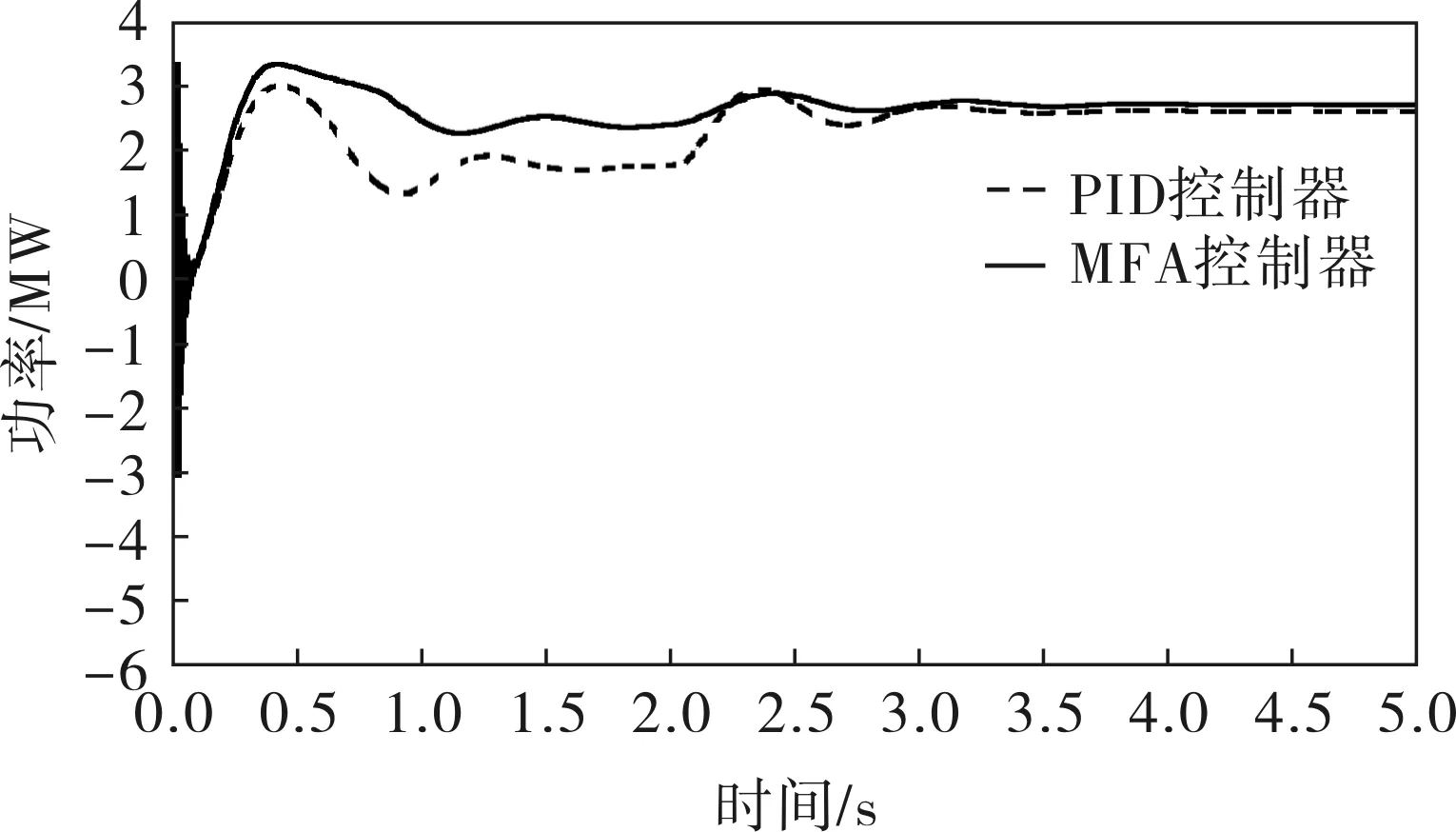
圖2 階躍風速下風力機功率效應曲線

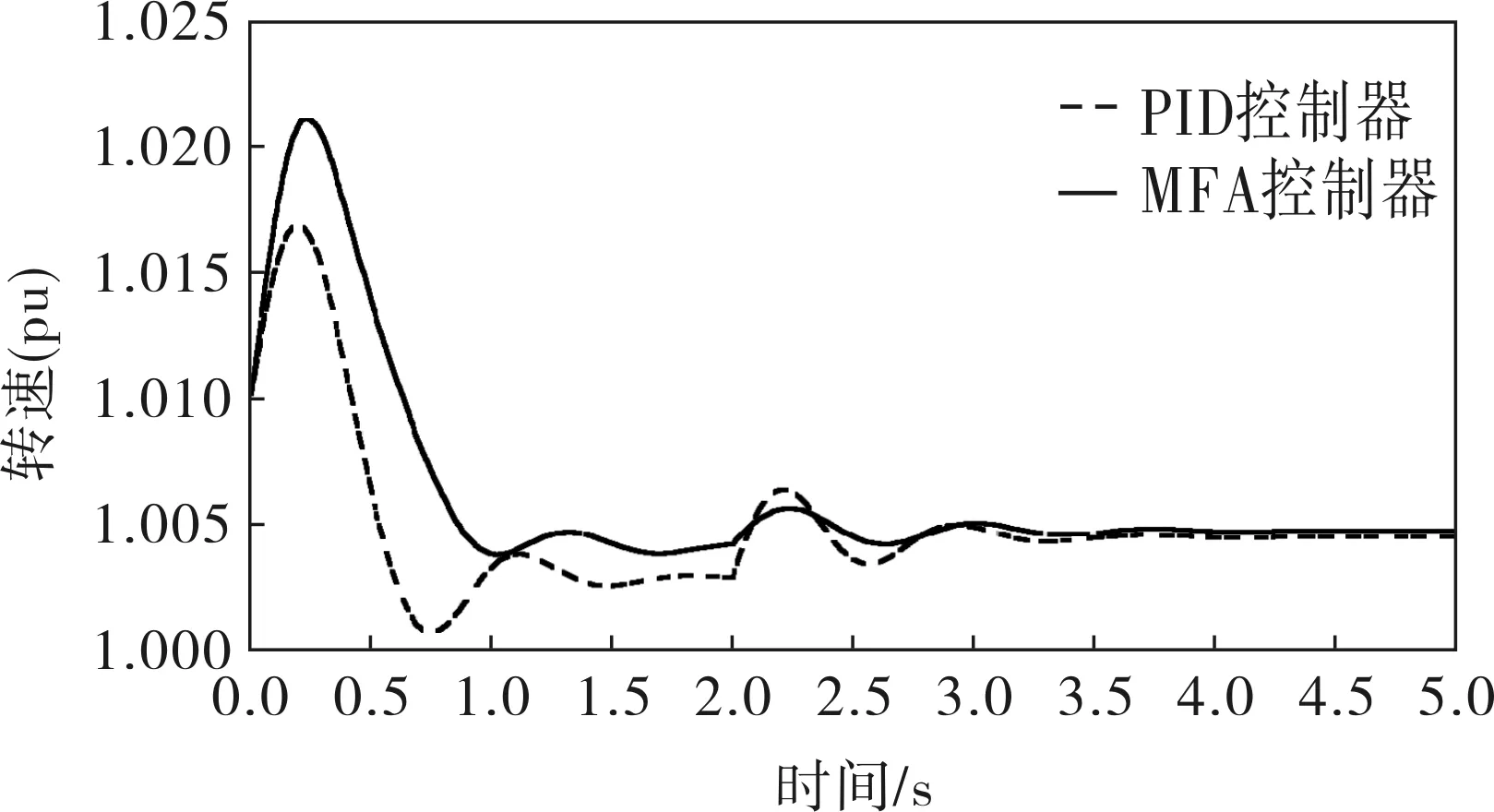
圖3 階躍風速下風力機角速度曲線

當風速為隨機風速時，所得發電機功率和風力機轉速曲線如4～6所示。

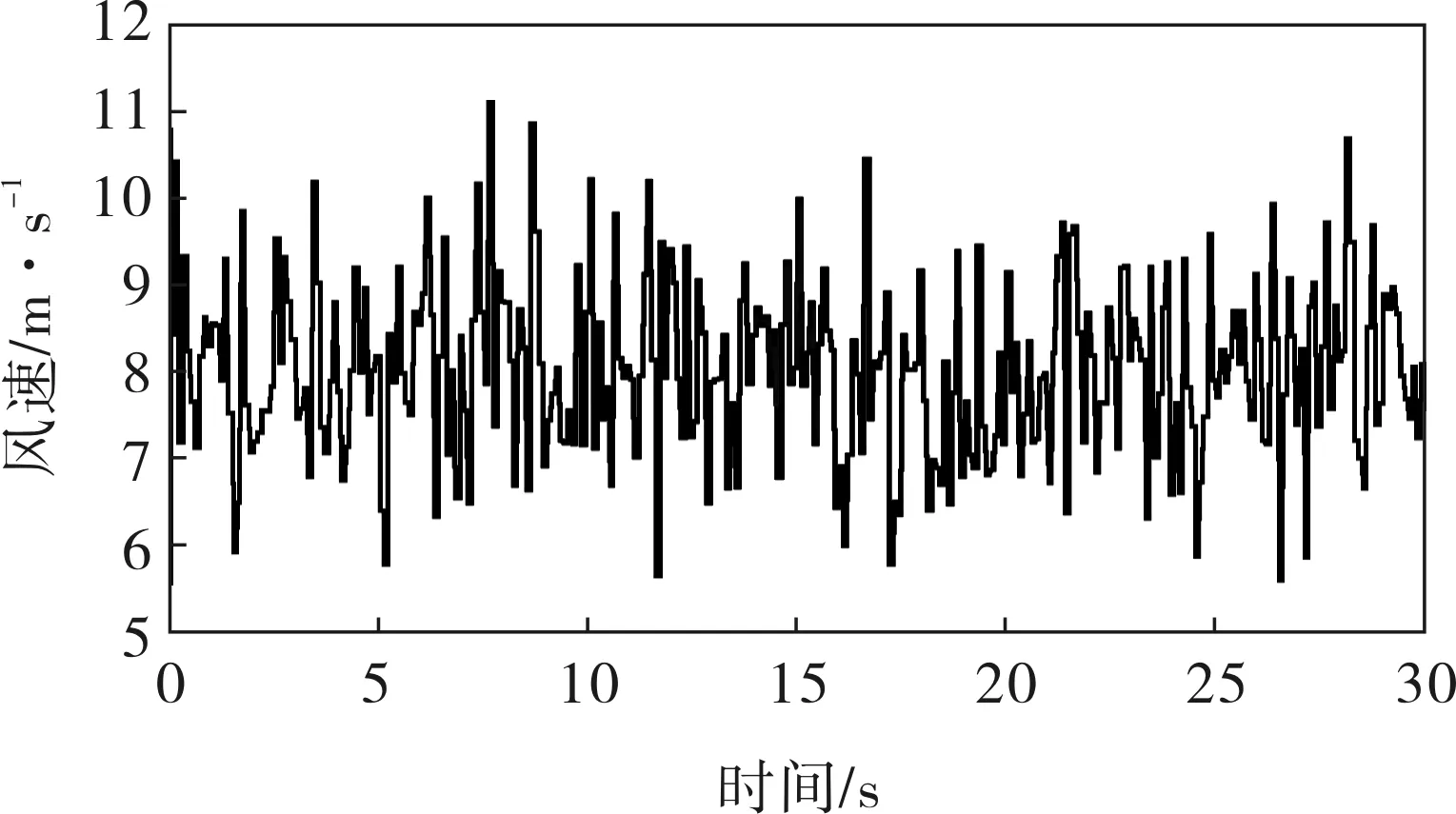
圖4 隨機風速實驗曲線

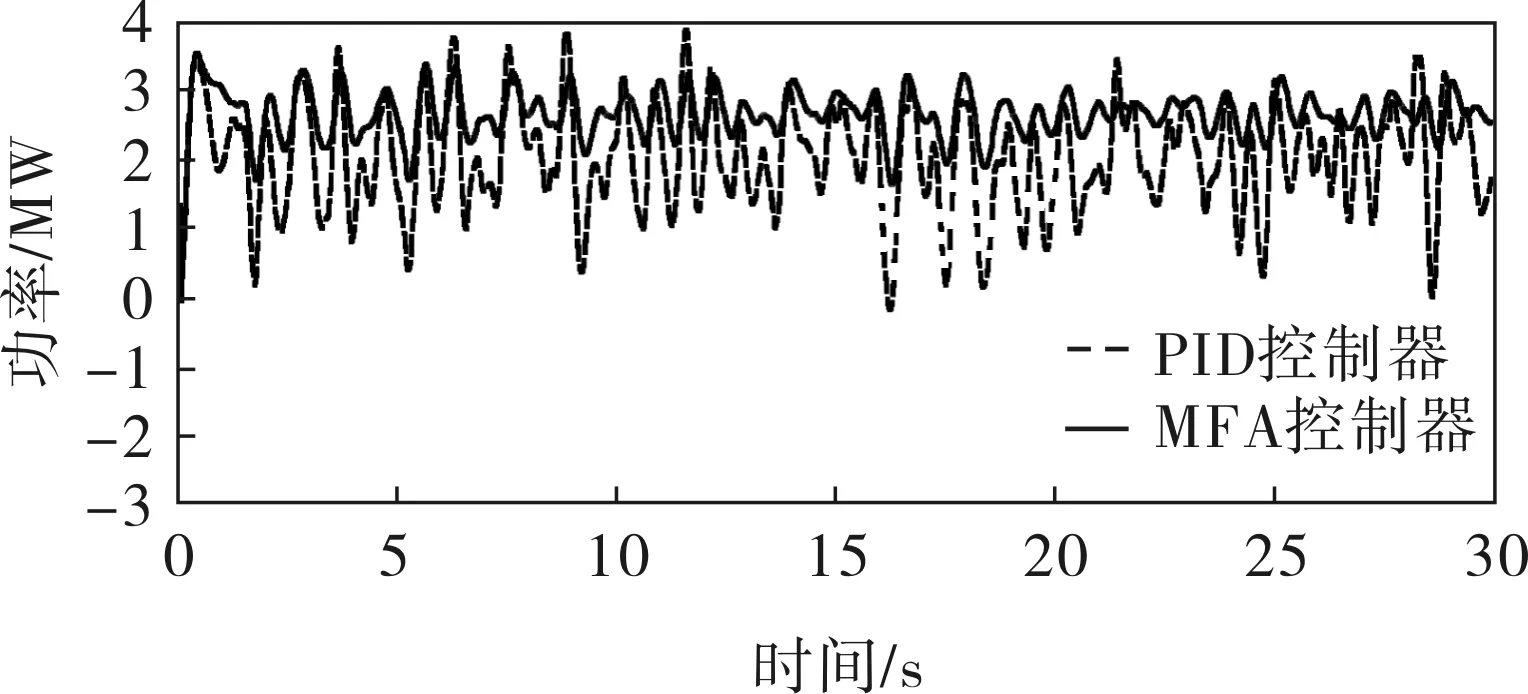
圖5 隨機風速下發電機功率曲線

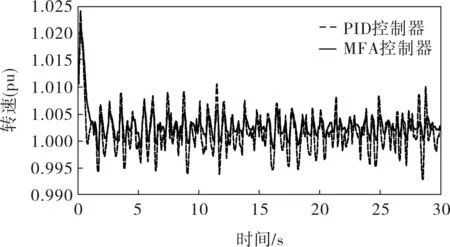
圖6 隨機風速下風力機角速度曲線

5 結束語

風力發電系統是一個非線性、強耦合的系統，并且風速的擾動性也極強。無模型自適應控制基于系統特性值動態估計，優化內部參數使系統克服時變和非線性，滿足系統動態和穩態要求。從實驗結果也可以看出，當風速在階躍風速和隨機風速下時，MFA控制器的控制效果明顯要好于PID控制器的，能夠更好地保持發電機的功率在額定功率下的穩定，實現恒功率控制。原因在于無模型自適應控制器能夠適應于非線性、強耦合系統，并且其抗干擾能力要強于PID控制，因此無模型自適應控制要明顯優于PID控制。

[1] 羅秋濱，李秀英，韓志剛.無模型控制方法的抗干擾能力分析[J].系統仿真學報，2008，20(13)：3472～3476.

[2] 蔣愛平，李秀英，韓志剛.從PID到無模型控制器[J].控制工程，2005，12(3)：217～221.

[3] 韓志剛，蔣愛平，汪國強.無模型控制方法對多變量耦合系統控制的應用研究[J].控制與決策，2004，19(10)：1155～1158.

[4] 曹榮敏，侯忠生.無模型控制方法在直線電機控制中的仿真研究[J].系統仿真學報，2006，18(10)：2874～2877.

[5] 金尚泰，侯忠生，王衛紅.無模型自適應控制方法在永磁直線電機控制中的應用[C].Proceedings of the 26th Chinese Control Conference.Zhangjiajie：IEEE,2007：748～751.

[6] 秦生升，胡國文，顧春雷，等.風力發電系統的恒功率非線性H∞魯棒控制[J].控制理論與應用，2012，29(5)： 617～622.

[7] 楊俊華，鄭儉華，楊夢麗，等.變漿距風力發電機組恒功率反饋線性化控制[J].控制理論與應用，2012，29(10)： 1365～1370.

[8] 張純明，姚興佳，張忠叢，等.模型參考自適應電動變槳距控制[J].控制理論與應用，2008，25(1)：148～150.

[9] 賀益康，胡家兵，徐烈.并網雙饋異步風力發電機運行控制[M].北京：中國電力出版社，2012.

[10] 王江.風力發電變槳距控制技術研究[D].合肥：合肥工業大學，2009.

[11] 侯忠生，韓志剛.非線性系統魯棒無模型學習自適應控制[J].控制與決策，1995，10(2)：137～142.

[12] 韓志剛.無模型控制器的設計問題[J].控制工程，2002，9(3)：19～22.