基于無差拍的永磁同步電動機直接轉矩控制方法研究
唐紅雨,劉賢興
(1.鎮江高等專科學校,鎮江212003;2.江蘇大學,鎮江212013)
0 引 言
永磁同步電動機(以下簡稱PMSM)以其可靠性好、效率高、適應性強、性價比高而被廣泛應用于各種高性能伺服系統中。直接轉矩控制(以下簡稱DTC)是一種較成熟的控制策略,無需對被控模型進行解耦計算,具有動態性能較好、魯棒性好、控制律不復雜等優點[1]。DTC 是將磁鏈和電磁轉矩作為控制變量,利用簡單的滯環比較器完成解耦控制,但轉矩和磁鏈脈動大,可調節性差。國內外學者對控制算法進行了研究與改進,其中無差拍控制技術由于其獨特的性能,引起了研究人員的關注。無差拍DTC 目標是讓轉矩和磁鏈在一個采樣周期結束時與給定值的誤差為零,具有較快的響應速度,在高速微處理芯片上易于實現[[2];文獻[3-5]從理論上可得到電機的磁鏈和轉矩無差控制的最佳參考電壓矢量,但增加了復雜性,求解狀態變量的計算大,物理意義不明確。文獻[6]研究了在電壓源逆變器輸出電壓受限條件下,無差拍DTC 的設計與實現問題。文獻[7]為了減小延時并提高伺服系統電流環控制性能,提出了一種基于無差拍控制原理的PMSM 魯棒預測電流控制算法。文獻[8]基于拉格朗日插值的無差拍預測控制算法,提出一種改進無差拍預測控制算法。文獻[9]提出一種新型的基于預測算法感應電機無差拍DTC 方法。
以上文獻多是研究了異步電機的無差拍DTC方法,從理論上可以推導出轉矩和定子磁鏈控制律,但實際采樣周期受限,還不能滿足在1 個周期實現誤差為零。同時,PMSM 本身的結構、性能與異步電機的區別,因而研究無差拍DTC 在PMSM 系統中的應用有一定的實際意義。本文對空間矢量脈寬調制(SVPWM)的電壓矢量計算方法進行改進,采用在一個周期內2 次采樣、2 次更新的策略,設計了PMSM在旋轉坐標系下的無差拍DTC,以角速度為輸入狀態變量,并通過擴張觀測器獲取磁鏈和轉矩的信號,該控制策略具有較好的動態響應,同時能夠減小轉矩和磁鏈脈動,提高系統控制的綜合性能。
1 PMSM 數學模型
PMSM 在旋轉坐標系dq 下的轉子磁通定向的電壓回路方程如下:
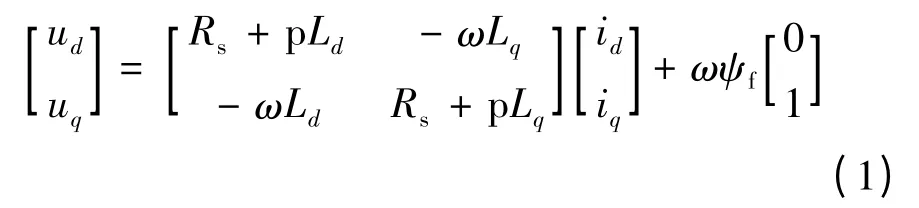
磁鏈方程:
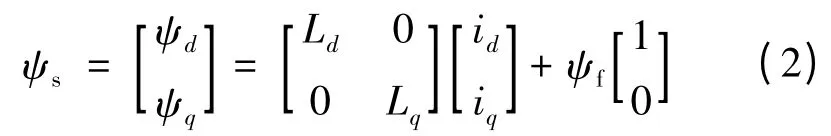
轉矩方程:
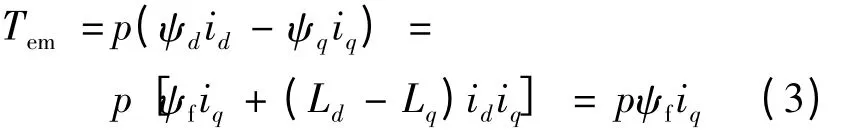
式中:p 為微分算子;id,iq和ud,uq分別為電機的d軸和q 軸的電流和電壓;Rs為電機的定子電阻;Ld,Lq分別為電機d 軸和q 軸的電感;對凸極式PMSM,存在Ld=Lq=L;ψs為定子磁鏈;ψf為電機的永磁通;Tem為電機扭矩;p 為電機的極對數;ω 為電機的角速度;B 和J 為電機的粘性摩擦系數和轉動慣量。
2 SVPWM 改進設計
2.1 SVPWM 占空比
對于電壓型PWM 逆變器,其輸出電壓空間矢量如圖1 所示。下面以扇區2 為例,分析PWM 信號調制和占空比,對于給定電壓矢量幅值Um,各個矢量輸出矢量時間由式(4)計算:
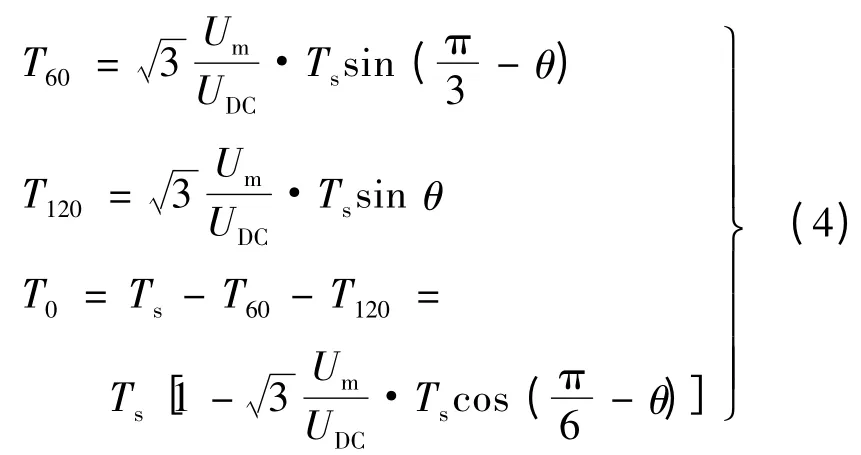
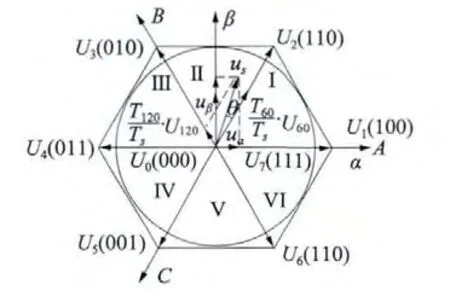
圖1 電壓空間矢量分布圖
2.2 PWM 更新時序改進策略
對于SVPWM 而言,在每個扇區內電壓矢量都不相同,目前在PWM 采樣、更新主要有2 種模式,如圖2 中模式1 和模式2 所示。
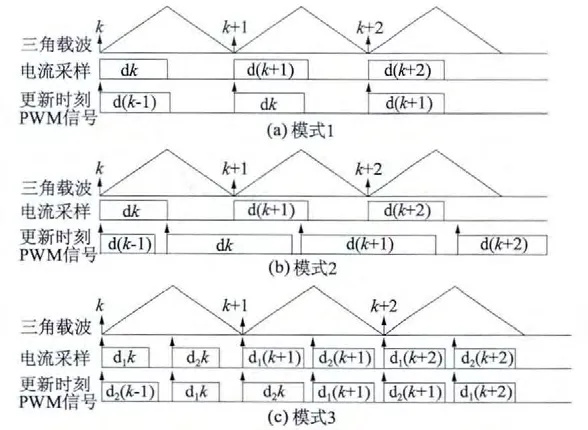
圖2 3 種PWM 更新策略對比
本文設計雙采樣雙更新,即在每個周期開始和中間時刻進行本周期的采樣時,同時把PWM 更新到上個周期的指令中,故采樣PWM 更新算法總共延時時間不會超過0.75Ts。如圖2 的模式3 所示,表1 為三種更新模式的延時時間對比。

表1 PWM 更新模式延時時間
3 無差拍直接轉矩控制律
3.1 dq 坐標系下的控制律
從定子磁場定向坐標上,可以設想ud控制磁鏈,而uq控制轉矩。無差拍控制[10-13]是在第k 個載波周期 [kTs,(k+1)Ts]開始時刻kTs,采樣得到的實際磁鏈和轉矩,計算得到磁鏈和轉矩的偏差Δψf和ΔTem,計算得到參考電壓矢量,然后運用SVPWM方法合成輸出電壓,使得在(k +1)Ts時刻的實際磁鏈和轉矩Tem跟蹤參考值和,Δψf=0,ΔTem=0。Ts為采樣周期,考慮到數字控制的采樣時間足夠小,將式(1)轉為電流形式后離散化:
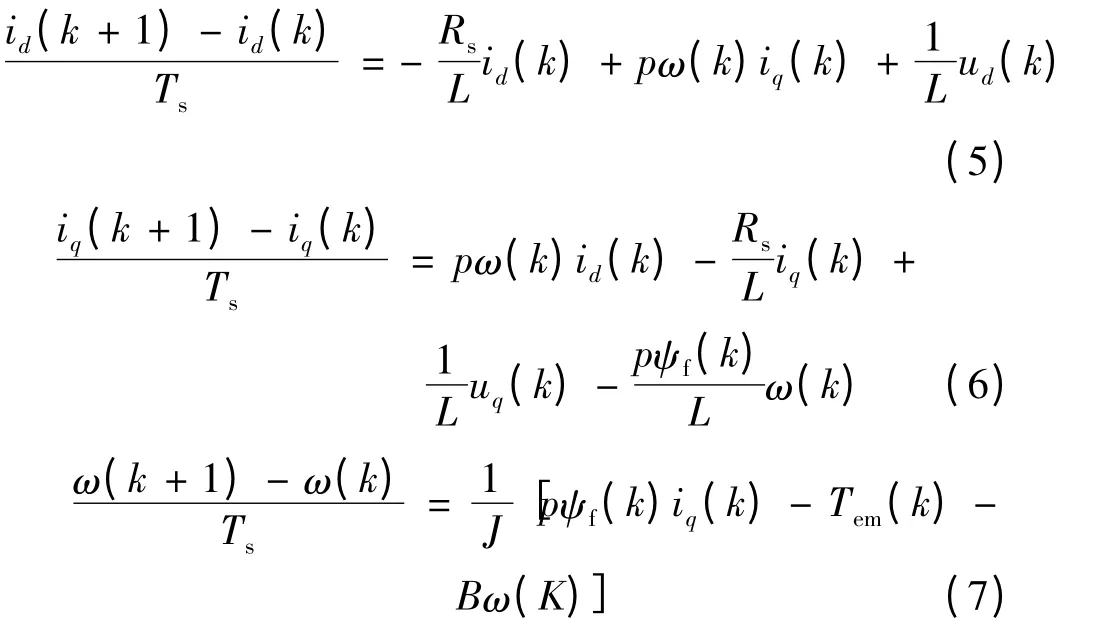
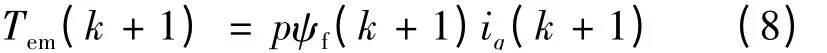
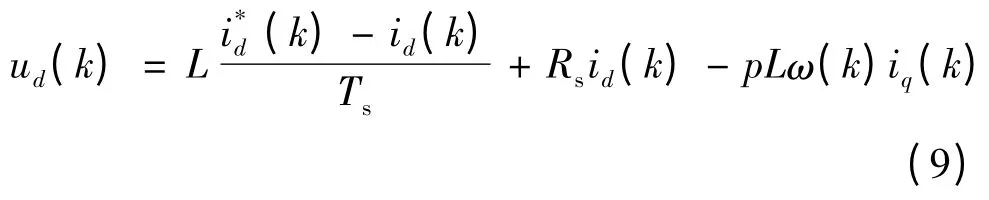
無差拍DTC 的思想就是要求在k +1 時刻的電機轉矩等于k 時刻的轉矩給定值,即:Tem(k +1)=(k),則相應的q 軸電流在k+1 時刻:
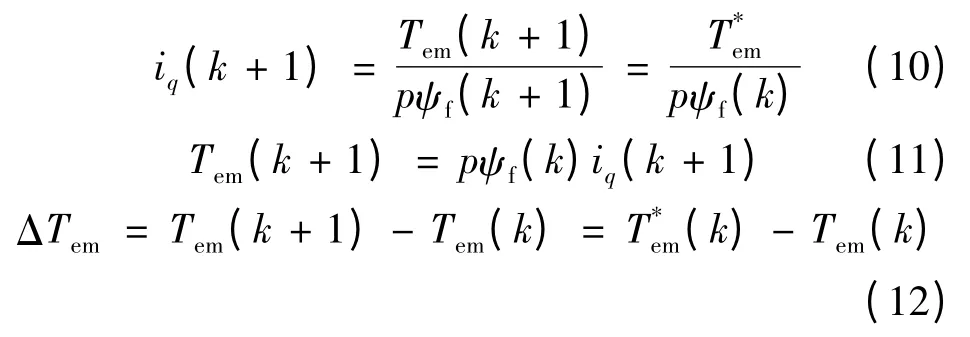
即:
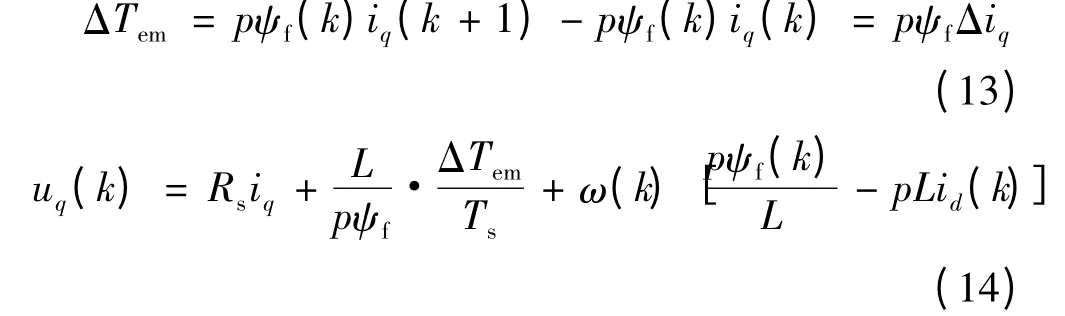
式(9)和式(14)中的ud(k)和uq(k)即是實現無差拍控制所需的電壓。
3.2 擴張狀態觀測器(ESO)估計
在電機運行過程中,電機參數會因發熱、磁飽和、dq 軸電流幅值、相角變化而變化,引起誤差。因此采用ESO 將所有參數變化對電流id,iq的影響分別用一個附加項表示[15],即:
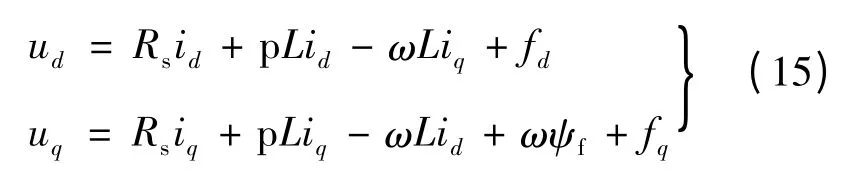
通過觀測補償這個附加項,可抑制系統參數變化,實現誤差矯正,提高系統魯棒性,ESO 可表示:
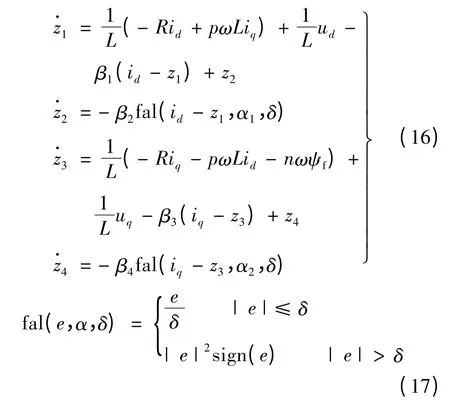
式中:z1,z3分別為id,iq觀測值;β1,β2,β3和β4為可調參數。在原點附近采用函數fal(e,α,δ)能夠消除高頻抖震,并實現控制增益隨誤差的變化而變化,δ為原點附近線性段的區間長度,α1,α2為可調參數,通常在0 到1 之間選擇。ESO 只需利用原對象的輸入和輸出信息進行觀測,釆用通用方法設計ESO 的參數β1,β2,β3和β4,保證觀測器的穩定性和快速性。將需要觀測的部分擴充為fd,fq的觀測值z2,z4,將其前饋補償到式(15)中,可實現對參數變化誤差的補償。
4 系統控制結構圖
PMSM 無差拍DTC 結構圖如圖3 所示,在α-β坐標系下,電機的電壓、電流信號和轉速信號由傳感器測出,定子磁鏈ψsα,ψsβ,θ 和轉矩根據模型由ESO計算得出,然后將磁鏈、電流轉換到兩相旋轉坐標系下,得到ψsd,ψsq,id,iq,ω 和Tem,再與給定值和比較,得到和ΔTem,再計算實現無差拍控制所需的ud,uq,通過SVPWM 計算出求出完整的空間電壓參考矢量后和作用時間,經dq/αβ 轉換環節,利用直流母線電壓和定子三相電流,計算得出SVPWM所需兩相靜止坐標系下參考電壓矢量uα,uβ,使實際電機轉矩達到期望值。在無差拍控制器之前,引入PI 環節實現調節,減少環境對電機參數的影響,降低定子磁鏈幅值和電壓的波動,提高狀態量觀測的準確性。
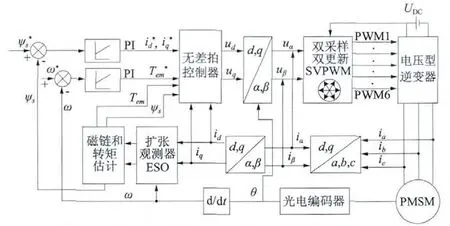
圖3 PMSM 無差拍DTC
5 仿 真
在MATLAB 中分別建立PMSM 無差拍DTC 和傳統DTC 控制系統,PMSM 參數如下:額定功率PN=1.5 kW,額定電壓UN=380 V,額定轉速nN=3 000 r/min,額定電流IN=3.5 A,極對數p =4,定子電阻RS=2.01 Ω,轉子電阻Rr=11 Ω,電感Ldq=0.237 8 mH,J=0.011 kg·m2,ψf=0.8 Wb,逆變器開關頻率為10 kHz,觀測器參數β1=100,β2=300,β3=800,β4=600,α1=0.5,α2=0.25,系統給定磁鏈為0.2 Wb。圖4 和圖5 分別為傳統DTC 和無差拍DTC 的定子磁鏈軌跡圖和電磁轉矩仿真圖。
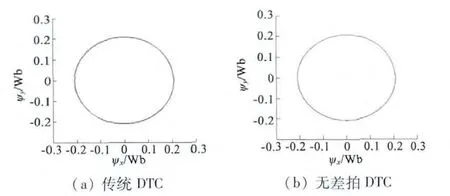
圖4 磁鏈仿真
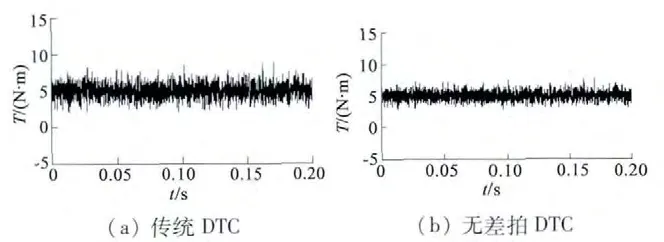
圖5 轉矩仿真
從圖4 的磁鏈仿真軌跡看出,無差拍DTC 減小了磁鏈脈動,從圖5 可以看出,無差拍DTC 有效降低了轉矩脈動,提高系統的魯棒性。圖6 為給定轉速為1 200 r/min,電動機起動時負載轉矩為0,電磁轉矩為5 N·m,5 s 突加負載轉矩2 N·m 時兩種方案系統響應情況對比。
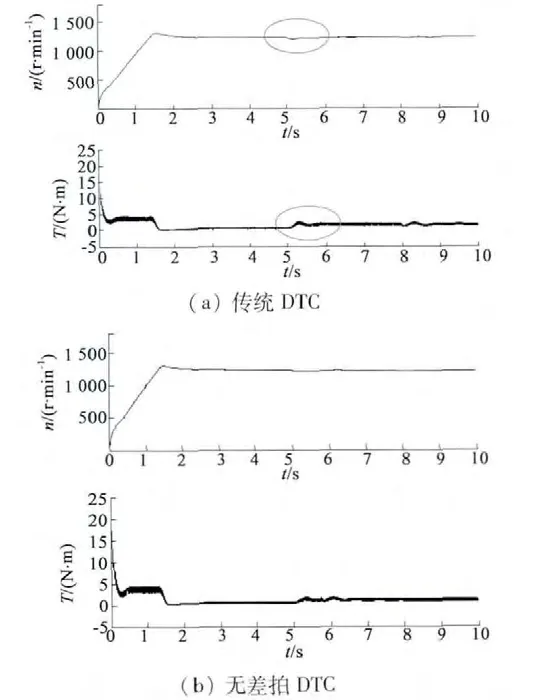
圖6 突加負載響應時的轉速與轉矩對比
從圖6 可以看出,無差拍DTC 具有較強的抗負載擾動,在突加負載的情況下,轉矩和轉速幾乎不會發生波動。圖7 為傳統DTC 和無差拍DTC 的PWM電壓信號跟蹤仿真圖,圖8 為兩種控制方法下的電壓跟蹤對比。
從圖7 看出,基于傳統DTC 算法的PWM 的輸出信號和期望值之間有滯后,而無差拍DTC 電壓信號只有0.75Ts,幾乎無滯后。從圖8 看出,無差拍DTC 比傳統DTC 快0.5 s。
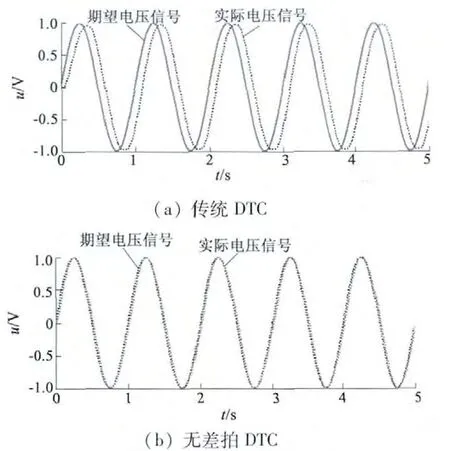
圖7 PWM 電壓信號
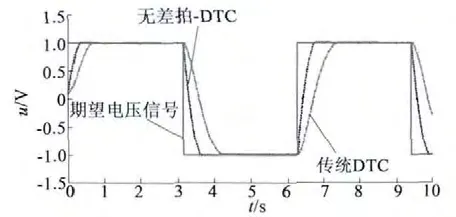
圖8 兩種方法的電壓跟蹤對比
6 結 語
本文分析了SVPWM 控制和傳統DTC 的優點,針對PMSM 的特點,結合了無差拍和DTC 的優點,提出了PMSM 無差拍DTC 方案。通過分析傳統PWM 占空比的不足,提出2 次采樣與更新策略,有效地減小了延時。根據PMSM 在旋轉坐標系下的數學模型,設計了擴張狀態觀測器,以定子磁鏈、轉子磁鏈和角速度為狀態變量,以電機參數變化為擾動量,在定子磁鏈定向坐標系中,理論上推導出PMSM 的無差拍直接轉矩電壓控制律,仿真實驗證明此方法能夠降低磁鏈和轉矩的脈動,具有較強的魯棒性、良好的動靜態性能。
[1] 聶晶,張興華,孫振興.效率最優的感應電機無差拍直接轉矩控制[J].電氣傳動,2013,10(43):23-27.
[2] 廖永衡,馮曉云,王珍.無差拍空間矢量調制直接轉矩控制簡化設計[J].電工技術學報,2011,6(6):95-101.
[3] 嚴殊,肖建.一種無差拍直接轉矩控制方法[J].電機與控制學報,2007,11(2):125-129.
[4] WEST N T,LORENZ R D. Implementation and evaluation of a stator and rotor flux linkage-based dead-beat,direct torque control of induction machines at the operational voltage limits[C]//2007 Industry Application Conference,42nd IAS Annual Meeting.2007:690-695.
[5] 王斌,王躍,王兆安.無速度傳感器的永磁同步電機無差拍直接轉矩控制方法[J].電機與控制學報,2014,6(6):42-49.
[6] 張興華,孫振興,沈捷.計及逆變器電壓輸出限制的感應電機無差拍直接轉矩控制[J].中國電機工程學報,2012,7(32):79-85.
[7] 牛里,楊明.基于無差拍控制的永磁同步電機魯棒電流控制算法研究[J].中國電機工程學報,2013,5(15):80-88.
[8] 鄭黎明,畢廣明,吳捷.應用SVM 的異步電動機直接轉矩控制仿真[J].微特電機,2008,36(5):49-51.
[9] 王晶鑫,姜建國.基于預測算法和變結構的矩陣變換器驅動感應電機無差拍直接轉矩控制[J].中國電機工程學報,2010,30(33):65-69.
[10] 劉英培,萬健如,梁鵬飛.基于擴展卡爾曼濾波器和空間電壓矢量調制的永磁同步電機直接轉矩控制[J]. 中國電機工程學報,2009,29(27):67-74.
[11] GUO You-gui,CHEN Cai-xue.Direct torque control system for induction machine fed by space vector modulated matrix converter[J].Control Theory & Applications,2008,4(2):383-388.
[12] 徐艷平,鐘彥儒.扇區細分和占空比控制相結合的永磁同步電機直接轉矩控制[J].中國電機工程學報,2009,29(3):102-108.
[13] 周揚忠;許海軍.直接轉矩控制永磁同步發電機相位自校正型定子磁鏈觀測器[J].中國電機工程學報,2012,6(18):98-108.
[14] YANG S M,LEE C H.A deadbeat current controller for field oriented induction motor drives[J].IEEE Transactions on Power Electronics,2002,17(5):772-778.
[15] KENNY B H,LORENZ R D.Stator and rotor-flux-based deadbeat direct torque control of induction machines[J].IEEE Transactions on Industry Application,2003,39(4):1093-1101.

