車用永磁電機電磁振動與噪聲分析

倪明明，廖連瑩，2，左言言，梅曉銘，耿玉芝

(1.江蘇大學，鎮江212013;2.常州工學院，常州213002)

0 引 言

永磁電機在給混合動力汽車帶來輕便的輔助動力時，也改變了它的噪聲、振動和聲振粗糙度(NVH)性能。雖然電機在工作過程中，產生的電磁噪聲聲壓級比傳統汽油機要小得多，但是該噪聲頻率很高［1］，而人耳對高頻噪聲又極其敏感，因此合理分析和降低電磁噪聲對改善混合動力汽車的NVH 性能，顯得很有必要。本文聯合使用JMAG，LMS Virtual. Lab 軟件，通過數值模擬的方式，對比某車用永磁電機在工作過程中不同位置處的振動位移響應和聲壓級變化情況。另外，還分析了不同模態阻尼下電機輻射聲壓級的衰減效率，為電機的減振降噪提供理論指導。

1 永磁電機電磁噪聲理論分析

1.1 負載凸極同步電機徑向力波

凸極永磁同步電機徑向力波可由Maxwell 方程得出［2］:

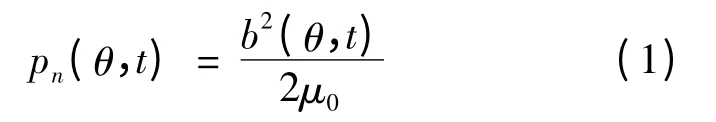
式中:pn(θ，t)單位為Pa，b(θ，t)為氣隙磁密，真空磁導率μ0=4π×10－7H/m。

空載時，忽略飽和狀態，氣隙磁密可以表示:

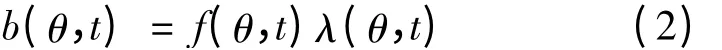
式中:f(θ，t)為氣隙磁勢;λ(θ，t)為氣隙磁導。

負載狀態下，除了空載主極磁場外，轉子中還產生電樞反應磁場，此時氣隙磁密幅值如下:

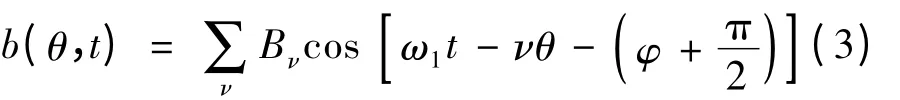
式中:Bν為電樞磁場ν 次諧波磁密幅值，且滿足:

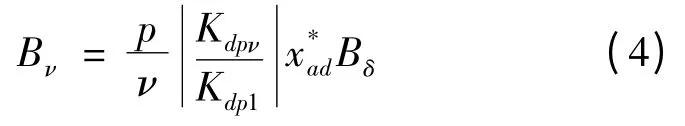
1.2 電磁振動與噪聲分析

如圖1 所示，電機在工作過程中會受到來自定子內表面的徑向力波pn(θ，t)而產生電磁振動，最終輻射到空氣中，成為電磁噪聲。

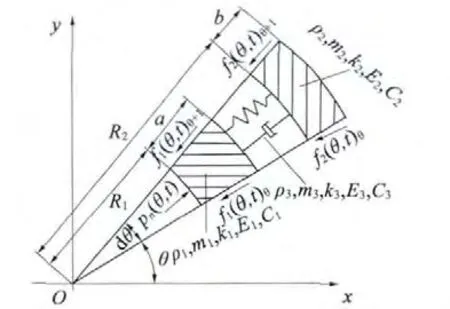
圖1 永磁電機振動模型

設定子鐵心、外殼和連接筋的密度，質量，剛度，彈性模量以及阻尼分別為ρ1，m1，K1，E1，C1;ρ2，m2，K2，E2，C2;ρ3，m3，K3，E3，C3;同時鐵心和外殼還受到相鄰剖切段的剪切力f1(θ，t)θ，f1(θ，t)θ+1和f2(θ，t)θ，f2(θ，t)θ+1。另外ζ 為系統阻尼比，根據帶耗散度的拉格朗日方程可以得到電磁振動方程為:

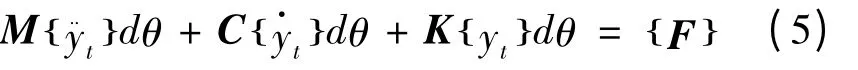
式中:M，C，K，F 分別為定子結構的質量矩陣，阻尼矩陣，剛度矩陣和激勵力矩陣，其值分別如下:

1.3 電磁噪聲分析

為了有效描述定子結構的自由輻射聲場，以下引入自動匹配層ΩAML(簡稱AML 層)作為虛擬的聲學邊界，電磁噪聲至ΩAML外包絡面時恰好被完全吸收［3－5］。當需要計算ΩAML以外的聲場時，以之作為激勵，計算其產生的輻射噪聲，從而描述整個自由聲場的聲輻射問題。

含AML 邊界的3 維頻域Helmholtz 方程:

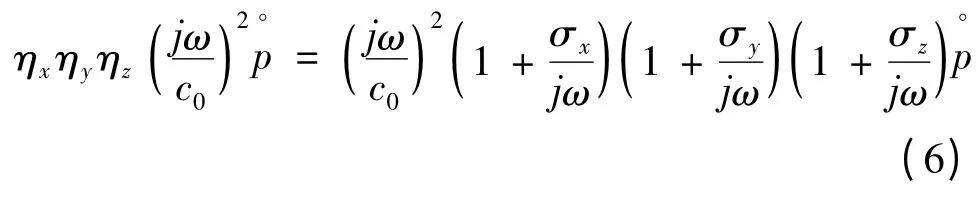
式中:σi代表i(i=x，y，z)方向的聲波衰減函數，且衰減效率ηi。為了便于化簡，這里引入輔助變量u［6－7］，其在x，y，z 上的投影如下:

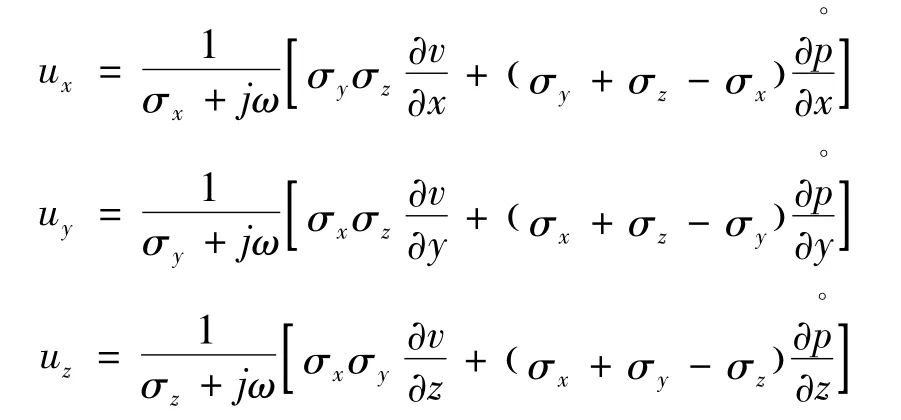
將u 代入式(10)，可以得到基于AML 方法的空間3維自由場聲輻射問題如下:

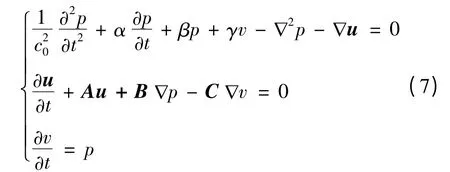
2 氣隙磁場有限元分析

本文采用JSOL 公司的JMAG 軟件仿真永磁電機，該電機為8極48槽，三相單層繞組，常用轉速1 200 r/min，永磁體矯頑力為920 000 A/m，相對磁導率為1.03，單匝等效繞組峰值電流為250 A［8－9］。其1 200 r/min 下某一時刻瞬態磁通密度云圖如圖2所示。

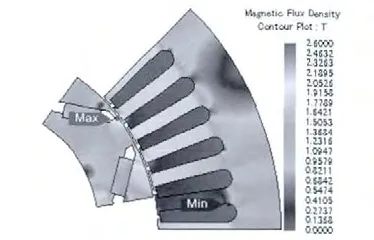
圖2 1 200 r/min 下某時刻磁通密度云圖

由圖2 可以看出，對定子結構產生影響的磁通密度主要集中在定轉子氣隙磁場以及定子槽與繞組接觸的地方，最大值可以達到2.6 T。為了清晰描述1 200 r/min 下徑向力波的變化，選取定轉子氣隙磁場中某一點的氣隙磁密頻譜如圖3 所示。

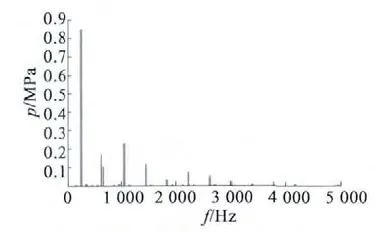
圖3 1 200 r/min 氣隙磁密頻譜

1 200 r/min 時電磁力波基波頻率為100 Hz，直流分量很小，只有1 887 Pa，不會對定子結構產生持續的靜壓力。二階低頻力波占主導地位，達到了0. 85 MPa，另外600 Hz，1 000 Hz，1 400 Hz以及2 200 Hz 和2 600 Hz 的中高頻力波幅值也相對較大，均可能引起定子結構較大的振動響應。

3 定子結構模態分析

該電機由機殼、定子鐵心、繞組、端蓋、轉子、永磁體、輸出軸、軸承等部分組成。由于定轉子之間是作用力與反作用力之間的關系，劃分網格時，如圖4所示，僅保留定子鐵心、外殼、端蓋、繞組以及軸承等部件［10］。

圖4 電機模型

為了便于劃分網格，將繞組線圈簡化為48 根銅條［11］。另外，為了表達出軸承的約束作用，同時簡化定子結構網格，本文將軸承簡化為2 個RBE2 單元，各部件的材料特性如表1 所示。

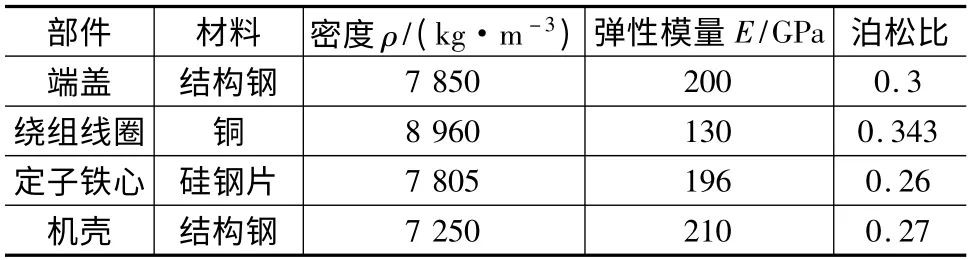
表1 定子結構材料屬性

限制軸承處3 個方向的平動自由度，計算定子結構前300 階約束模態振型，選取其前6 階振型如圖5 所示。由于定子結構沿傳動軸方向呈中心對稱，所以經常出現相鄰固有頻率非常接近的模態振型，這些模態除了在相位上存在差異，并無明顯區別。該定子結構的約束模態均為中高頻模態，其中前三階約束模態分別與第6 階和14 階力波頻率相接近，極有可能引起定子結構較大的電磁振動量。

圖5 約束模態振型

4 電磁振動與噪聲分析

4.1 電磁振動分析

將JMAG 仿真結果導入到LMS Virtual.Lab 中，并截取2 階氣隙電磁力，如圖6 所示。

圖6 二階氣隙電磁力

圖6 顯示電磁激勵力在空間沿徑向分層分布，在定轉子氣隙處以及定子與繞組相接觸的地方，電磁力幅值最大，二階最大電磁力僅1.82 N。使用模態疊加法計算定子結構在電磁激勵力下的振動位移響應，并提取機殼中點、機殼邊緣點、端蓋圓周孔邊緣點以及端蓋中心孔邊緣點的位移響應，如圖7 所示。

圖7 表明，X 方向上外殼中點振動位移最大，其次外殼邊緣點的振動響應量同比減小了30%左右;最后由于限制了端蓋中心孔的位移，該處的振動位移最小。這4 個監測點的響應頻率均出現在中低頻，其中150 Hz 的位移響應量最大，外殼中點X 方向達到了1.86 ×10－4mm。另外224 Hz，292 Hz 同樣出現了低頻響應量，達到了1.25 ×10－4mm 和1.47 ×10－4mm。除此之外，在1 502 Hz 和1 550 Hz的高頻區域，也出現了2 個較大的位移響應峰值點。

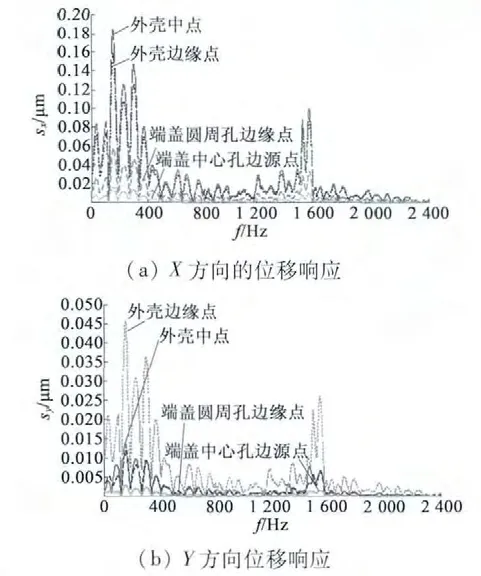
圖7 4 個觀測點的振動位移響應

在Y 方向上，這4 個監測點的峰值響應頻率與X 方向完全一致，僅僅在幅值上都小了一個數量級，這主要是因為電機在旋轉過程中，對X 方向產生了一個反向的沖力，該反力導致了定子在X 方向產生了更大的位移響應量。

4.2 電磁噪聲分析

如圖8 所示，本文以定子外殼位移響應作為邊界條件，采用AML 方法計算定子結構的輻射噪聲，同時使用XZ－YZ 相交垂直平面作為聲壓場點。計算電機在電磁激勵力作用下的A 記權聲壓級有效值，其某一階聲壓云圖，如圖9 所示。

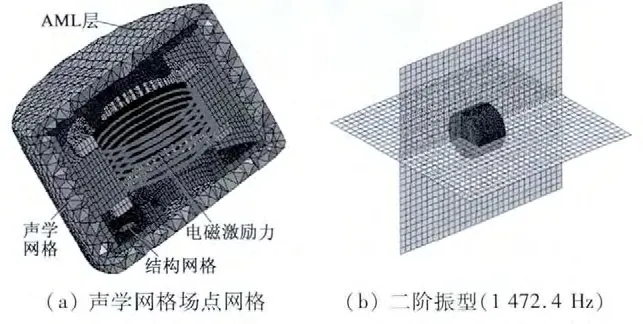
圖8 聲學網格和場點網格

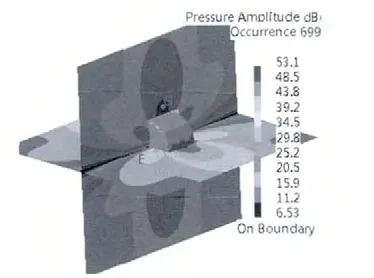
圖9 定子結構輻射聲壓分布

圖9表明該電機聲壓級最大值達到了53 dB(A)。由于軸承兩側受到約束，振動位移相對較小，因而軸承處定子輻射聲壓級明顯小于其他地方。如圖9 所示，選取靠近軸承、機殼中點以及靠近機殼邊緣的3個監測點，分析其在250 ～8 000 Hz 的A 記權聲壓級如圖10 所示。

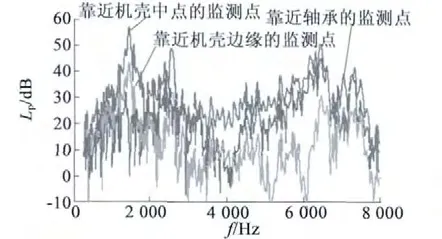
圖10 各監測點聲壓級有效值對比

250 ～2 000 Hz 中低頻段，3 個測點均在1 450 Hz 處出現峰值，靠近外殼中點、外殼邊緣點以及軸承處的聲壓級分別達到了57.03 dB(A)，43.22 dB(A)，31.91 dB(A)，這主要是由于外殼中點的振動位移響應明顯大于其他兩個測點。2 000 Hz 以后，靠近軸承的測點聲壓漸漸高于外殼邊緣點的聲壓，在5 500 Hz 以后，僅與靠近外殼中點的測點相差不到5 dB(A)，甚至在7 000 ～7 300 Hz 內，明顯超過了外殼中點的聲壓級，這主要是因為軸承處是不完全閉合的，電磁波可以從軸承間隙除輻射出來，且高頻電磁噪聲輻射能量較大，故而出現高頻段軸承處聲壓明顯變大的現象。

圖11 計算了0.5%、1%和2%模態阻尼下G 點的A 記權聲壓級有效值。

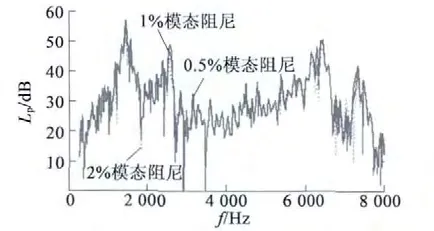
圖11 不同模態阻尼下聲壓級的變化

從總的頻段來看，模態阻尼對1 400 Hz 低頻噪聲和40 dB(A)以下的電磁噪聲基本沒有衰減作用，僅在1 450 Hz，2 550 Hz，6 440 Hz 以及6 950 Hz 的峰值響應頻率點對電磁噪聲有明顯的衰減作用，其中1 450 Hz 時，在0.5%，1%和2%模態阻尼下，聲壓級分別是57.03 dB(A)，54.39 dB(A)和49.96 dB(A)，衰減程度依次為4.6%和12.4%。同理，在2 550 Hz 時，衰減程度依次為3.2%和10.2%;6 440 Hz 時，衰減程度分別為1.2%和4.8%。由此看出，隨著頻率的增大，模態阻尼對電磁噪聲的衰減作用在逐漸下降。

5 結 語

(1)低階力波在電磁激勵力中占主導地位，定子結構中高階模態頻率遠遠大于激勵力頻率，對電磁振動結果影響不大;

(2)機殼中點振動位移響應量最大，軸承處振動位移響應量最小，電機工作過程中產生的切向反力使定子結構振動位移在X 和Y 方向的分量相差1個數量級左右;

(3)低頻段靠近軸承處聲壓級很小，隨著頻率的增大，靠近軸承位置的聲壓級迅速增大，但總的頻段來看，靠近外殼中點的聲壓級均明顯大于其他位置;

(4)模態阻尼對1 400 Hz 以下中低頻噪聲衰減作用很小，僅在1 400 Hz 以上的電磁噪聲峰值點出現明顯的衰減效果，且隨著頻率的增加，衰減效率在逐漸下降。

［1］ 陳秋明，陳勇.永磁同步電動機電磁振動噪聲機理研究［J］.微特電機，2013，41(8):1－5，19.

［2］ 陳永校，諸自強，應善成. 電機噪聲的分析和控制［M］. 杭州:浙江大學出版社，1987.

［3］ TURKEL E，YEFET A. Absorbing PML boundary layers for wave－like equations［J］. Applied Numerical Mathematics，1998，27(4):533－557.

［4］ 夏林樹.基于完美匹配層的無界條狀區域上Helmholtz 方程的譜方法［D］.廈門:廈門大學，2008.

［5］ SINGER I，TURKEL E. A perfectly matched layer for the Helmholtz equation in a semi－infinite strip［J］. Journal of Computational Physics，2004，201(2):439－465.

［6］ KALTENBACHER B，KALTENBACHER M，ImboSim. A modified and stable version of a perfectly matched layer technique for the 3－d second order wave equation in time domain with an application to aeroacoustics［J］.Journal of Computational Physics，2013，235:407－422.

［7］ KIM S，PASCIAK J E.Analysis of the spectrum of a cartesian perfectly matched Layer (PML)approximation to acoustic scattering problems［J］. Journal of Mathematical Analysis and Applications，2010，361(2):420－430.

［8］ HSU J S，，AYERS C W，COOMER C L，et al.Report on Toyota/Prius Motor Design and manufacturing Assessment［R］. US:Oak Ridge Nation Laboratory，2004.

［9］ AYERS C W，HSU J S，MARLINO L D，et al.Evaluation of 2004 Toyota Prius Hybrid Electric Drive System InterimReport［R］.US:Oak Ridge Nation Laboratory，2004.

［10］ 毛文貴，傅彩明，彭浩舸，等. 立式電機定子的振動特性仿真研究［J］.湖南工程學院學報(自然科學版)，2008，18(2):22－25，29.

［11］ 崔淑梅，于天達，宋立偉.基于ANSYS 和SYSNOISE 的電機噪聲仿真分析方法［J］.電機與控制學報，2011，15(9):63－67.