變頻調速系統(tǒng)低頻電壓補償規(guī)律探討

江春冬，田曉梅

(河北工業(yè)大學，天津300130)

0 引 言

變頻調速系統(tǒng)在基速以下進行調速時，常常要保證磁通為額定磁通，以保證既能充分利用電動機的鐵心出力，又不至于使磁路進入飽和狀態(tài)，磁阻過大，電機發(fā)熱嚴重。現(xiàn)有的開環(huán)變頻調速系統(tǒng)往往采用恒壓頻比控制，但恒壓頻比控制在高頻時控制精度還好，低頻時如果仍舊忽略定子漏阻抗上的壓降，則電磁轉矩下降較大，影響低頻帶載能力，故實際上市場上的通用變頻器異步電動機變頻調速系統(tǒng)基頻以下均采用帶低頻電壓補償?shù)暮銐侯l比控制［1－2］。

但是，低頻電壓應當補償多少?現(xiàn)有文獻中主要以恒定子電動勢頻率比為目標，補償時主要考慮負載大小和定子電阻的影響，對定子漏電抗補償結果的影響往往忽略。但無疑，電抗的大小對補償電壓也會有影響，影響有多大?是否可以忽略?本文從這個角度出發(fā)，試圖得到一些可供大家參考的結果。

1 低頻電壓補償規(guī)律

1.1 恒壓頻比控制思想的來源

如前所述，低頻時希望保證磁通恒定，由異步電動機穩(wěn)態(tài)時的磁動勢公式和定子電動勢平衡方程，當頻率較高，定子漏阻抗上的壓降較小，忽略之，定子電壓和感應電動勢的有效值相同，因此要保證變頻調速時磁通恒定，由式(1)，就要保證電動勢頻率比為恒值，而保證電動勢頻率比為恒值，只需要保證電壓頻率比為恒值就可以了。這就是恒壓頻比思想的由來［1，5］。

異步電動機磁動勢公式:

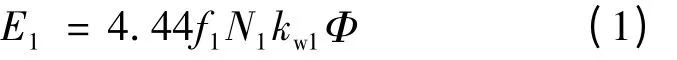
定子電動勢中衡方程:

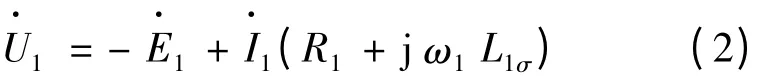
式中:f1為電源頻率;N1為定子每相繞組匝數(shù);kw1為定子繞組的繞組系數(shù);Φ 為氣隙磁通;U1為電源電壓;E1為定子反電勢;R1為定子電阻;ω1=2π f1;L1σ為定子漏電感。

1.2 恒壓頻比控制時的機械特性

采用恒壓頻比控制時，異步電動機機械特性表達式可寫成式(3)，由此繪制的機械特性如圖1 所示，可見，頻率越低，電壓越低，最大電磁轉矩越小，帶載能力越弱，但線性段的特性還是比較硬的［1］。

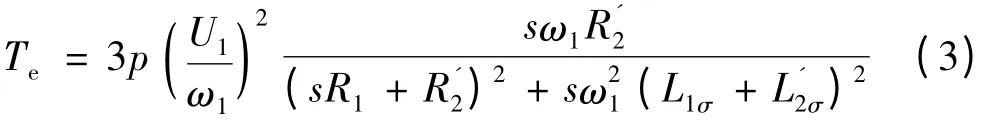
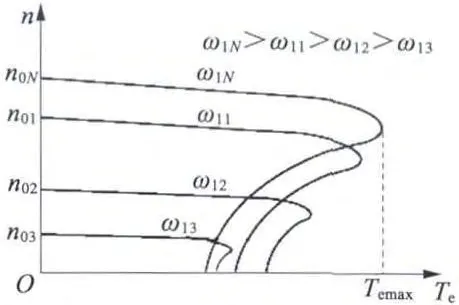
圖1 恒壓頻比控制時的機械特性

1.3 低頻電壓補償思想

為提高系統(tǒng)低頻帶載能力，就要考慮低頻時轉矩減小的原因。低頻時轉矩之所以減小，是因為低頻時電機漏阻抗上的壓降在式(2)中所占比重增大，如果忽略，得到的感應電動勢與實際值間誤差增大，磁通降低得多，電磁轉矩必然減小。所以低頻時需要進行電壓補償。

低頻電壓補償?shù)脑瓌t就是保證磁通為恒定值，因此要保證感應電動勢和頻率比為恒定值，由式(2)可知，定子電壓補償時應補償不同頻率下漏阻抗的壓降。理論上，實時檢測并補償本應最為有效，但又會出現(xiàn)新問題:本來通用變頻器異步電動機變頻調速系統(tǒng)因其簡單而在市場上占有一定的份額，如果需要實時檢測再反饋回來參與控制就失去了它的簡單性;同時由于低頻狀態(tài)不是常態(tài)，也沒有太大必要對此耗費代價，故現(xiàn)有的產品中主要補償?shù)氖遣煌撦d大小情況下電阻上的壓降，對負載的相位考慮較少。由此給出的補償線可提高低頻時的轉矩，如圖2 所示，雖不精確但可滿足一定的負載要求。此時的恒壓頻比控制特性如圖3 中b 線所示，它代表一定負載下的控制特性，如果負載增大，控制特性中低頻時的電壓可再適當增大［2，4－5］。

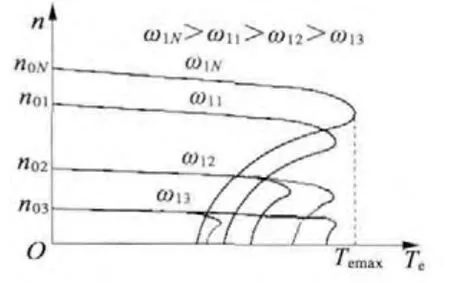
圖2 帶補償?shù)暮銐侯l控制時的機械特性

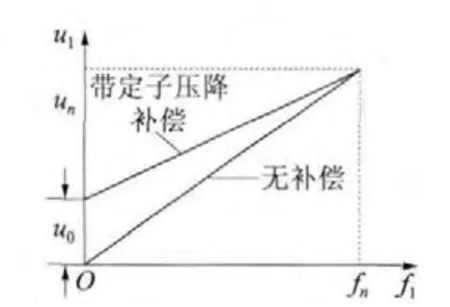
圖3 恒壓頻比控制特性

1.4 低頻電壓補償?shù)挠绊懸蛩?/h3>

在恒壓頻比控制方案中，低頻電壓補償?shù)哪康鼐褪菫榱颂岣呦到y(tǒng)的低頻帶載能力，其原則仍是保持穩(wěn)定時，磁通不變，即為額定磁通，也就是滿足式(1)，即滿足恒電動勢頻率比［1］。

由式(2)，可推出:

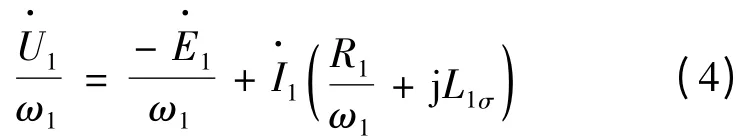
可見，除了定子電阻外，定子電流的相位和定子漏感一定會影響電壓的補償值，進而影響到系統(tǒng)低頻轉矩性能。

同時，低頻時電壓補償也不能太大，如果負載不變，電壓補償過大，將導致勵磁電流增大，磁通增加，鐵心飽和，勵磁電流波形發(fā)生畸變，嚴重時甚至引起變頻器因過電流而跳閘。所以補償要合理，一般情況下都不會進行完全補償，即無論頻率如何，電動機的最大電磁轉矩都不變。

2 定子電流相位對低頻電壓補償規(guī)律的影響

2.1 只考慮負載大小時的低頻電壓補償規(guī)律

這種補償規(guī)律是最常用的，在各種文獻上都可見到，其結果的推導可用一臺基本的電機數(shù)據(jù)給出變化趨勢。

一臺三相異步電動機的基本數(shù)據(jù)［3］:pN=10 kW，UN=380 V，IN=12 A，nN=1 450 r/min，R1=1.375 Ω，L1σ=7.735 mH，R'2=1.04 Ω，L'1σ=14.006 mH，cosφ1N=0.86，η1N=86.6%。

若要將式(3)中的矢量形式直接變成標量表達式，將會非常復雜。雖然可以用相量圖進行處理，但不同頻率下相量圖又會有差別，所以工作量會相當大。有研究人員研究矢量補償，但這種補償因為復雜，實用性很小。我們在現(xiàn)有的常用補償規(guī)律研究思路上，研究電流相位對補償電壓的影響。考慮實際中忽略定子阻抗上的壓降時，定子電壓與感應電動勢相位接近但相反，故在標量化時認為－ E·1與的方向相同，處理時才可直接將矢量上的點去掉變成標量形式。

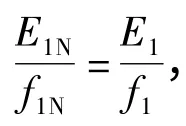
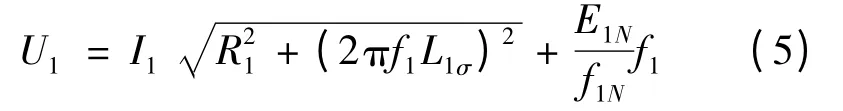
補償規(guī)律如圖4 所示。

考慮到低頻時f1較小，定子漏電抗較小，忽略它，只考慮定子電阻上的壓降，負載大小不同時補償電壓表示:

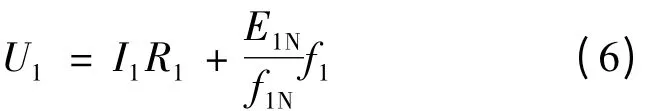
補償規(guī)律如圖5 所示。

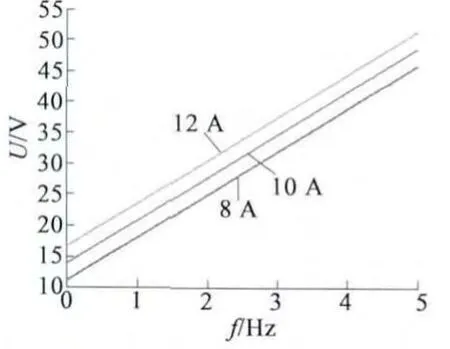
圖4 考慮定子漏磁阻抗和負載大小時定子電壓補償曲線

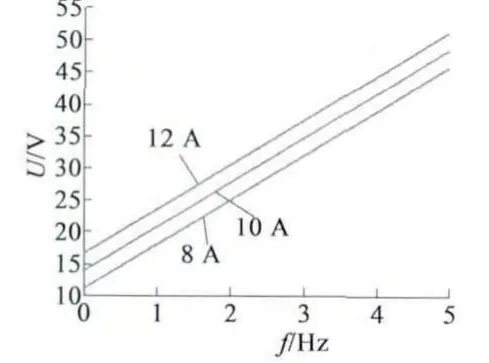
圖5 只考慮定子電阻和負載大小時定子電壓補償曲線

由圖4 和圖5 可以看出，二者變化趨勢接近相同，隨著負載的增大，定子電阻上的壓降越大，補償?shù)碾妷涸礁摺６N情況的微小差別在于，隨著頻率的增加，定子的漏電抗值增大，補償?shù)碾妷郝杂性龃蟆１容^2 Hz 情況下的二者電壓，前者為24.88 V，后者為24.86 V，差別很小，故常用的只考慮定子電阻的壓降而忽略電抗上的壓降對控制精度的影響不大。

2.2 考慮負載相位時的低頻電壓補償規(guī)律

由前面得出，低頻時定子漏電抗對補償電壓影響較小，故分析負載相位對補償電壓影響時忽略之，只考慮電阻壓降的影響。異步電動機為感性負載，設定子電流滯后電壓φ 角度，此時電動機定子電壓、感應電動勢和負載之間的相量圖可如圖6 所示。

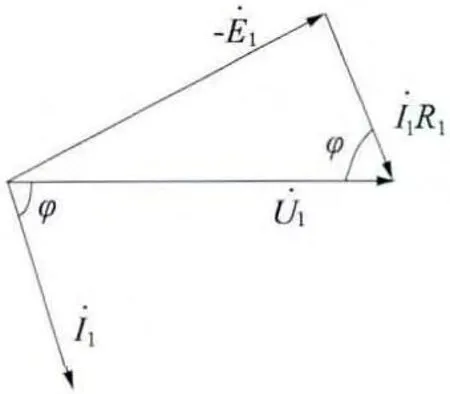
圖6 定子電壓、電流和感應電動勢間的向量圖

由圖6 與余弦定理可推出:

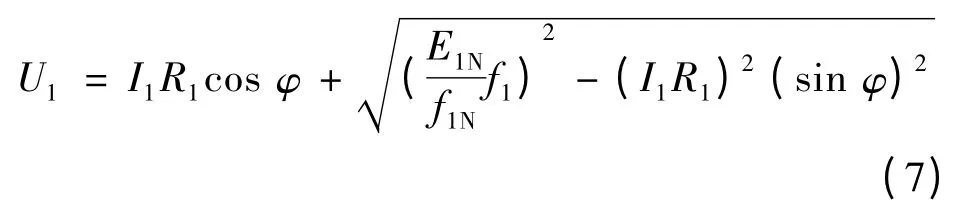
仍以前述電機參數(shù)為例，繪制負載的相位φ 分別為10°，30°，60°，負載電流為11 A 時的電壓補償曲線如圖7 所示。

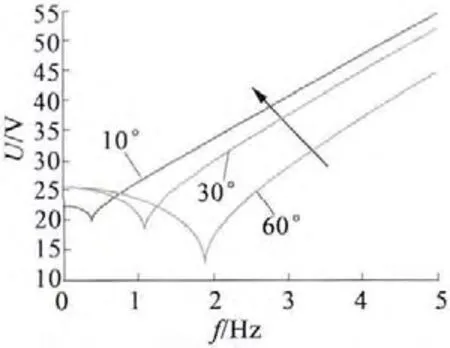
圖7 負載大小不變，考慮負載相位時的定子電壓補償曲線

從圖7 可以看出，隨著負載感性值的減小，補償?shù)碾妷褐禃龃蟆６翌l率很小時，電阻上的壓降比感應電動勢還大，補償電壓隨著負載電流的相位增大要更大一些。

3 結 語

每次遇到低頻電壓補償問題時，都會想到異步電動機的電壓平衡方程式(2)，定子電流的相位對阻抗上的壓降應該也有影響，但相關資料中卻很少有人考慮，于是本文對此進行了研究。本文只是從理論上進行了相關分析，實際意義可能不大。因為電動機帶的是有功的機械負載，負載一定時，影響到負載相位的是電動機的相關參數(shù)，當電動機參數(shù)不變時，同樣負載下同一電動機的定子電流的相位變化不大。

總結一下本文工作，得出如下結論供參考:

(1)考慮給一通用變頻器異步電動機變頻調速系統(tǒng)提供低頻電壓補償曲線時，如果只考慮負載大小，不考慮負載相位時，隨著負載的增大，補償電壓也要相應增大;而且考慮不考慮定子漏電感對補償電壓的影響不大。因此可直接考慮定子電阻上的壓降即可。

(2)考慮定子電流相位時，若負載大小不變，隨著定子電流滯后相位角的增加，補償電壓可適當減小。

［1］ 阮毅，陳伯時.電力拖動自動控制系統(tǒng)［M］. 第2 版:北京:機械工業(yè)出版社，2011.

［2］ 張健，曹建文，張愛玲.異步電機變頻調速系統(tǒng)低頻電壓自動補償?shù)难芯颗c實現(xiàn)［J］.太原理工大學學報，2008，39(5):508－510.

［3］ 唐海源，張曉江.電機及拖動基礎習題解答與學習指導［M］.北京:機械工業(yè)出版社，2006.

［4］ 陳小安，陳文曲.U/f 控制下高速電主軸的低頻電壓補償與負載特性分析［J］.機械工程學報，2011，47(9):132－138.

［5］ 朱高中.電壓補償在變頻調速系統(tǒng)中的應用研究［J］. 工礦自動化，2013，39(3):53－56.