總溫總壓測頭模態振型變化規律研究

陳 釗，付 饒

(中國飛行試驗研究院，陜西 西安 710089)

0 引言

采用測量耙測量航空發動機總溫總壓是發動機定型試飛中的主要測量手段之一［1］，發動機試驗時在相關氣流流通壁面上安裝溫度和壓力測量耙或測頭，如果測量耙或測頭的響應頻率與發動機的振動或氣流激勵頻率相吻合，會產生諧共振，使測量耙或測頭容易損傷甚至斷裂［2］。輕者測量耙或測頭不能正常工作，重者將損傷發動機轉動部件，危及飛機飛行安全。為確保測量耙或測頭工作安全，在設計試驗時除對其進行靜強度校核計算外，還必須進行模態分析計算［3］。

1 理論分析

由于測頭結構模型比較復雜，必須對模型進行簡化后再進行理論分析，將測頭簡化為懸臂梁進行理論分析，懸臂梁結構簡化如圖1所示。

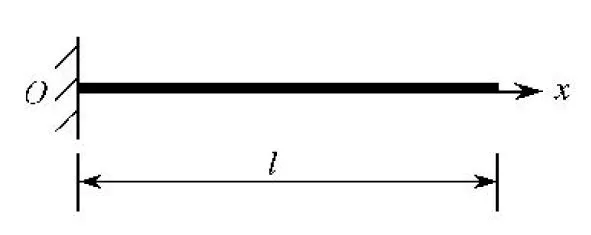
圖1 懸臂梁示意圖

設梁的長度為L，單位長度質量為ρ，抗彎剛度為EI，建立如圖1所示坐標系，水平方向為x方向，垂直方向為y方向，在任意瞬時t，某一微元段的Y向位移可以用y(x，t)表示，根據其受力情況，微元段Y向位移運動方程為:

忽略轉動慣量影響，各力對任一微元體的右截面上任一點的力矩之和應為0，即:

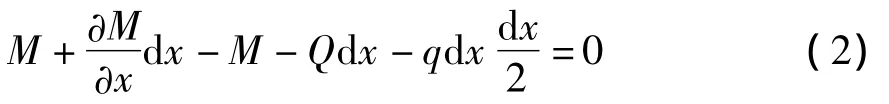
根據材料力學，彎矩與撓度曲線的關系為:

將公式(2)和公式(3)代入公式(1)得:

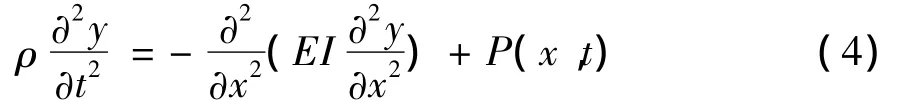
對偏微分方程(4)進行求解，得到表1結果。

表1 懸臂梁前5階特征根

其中對于i≥3的各特征根可足夠準確的取為:

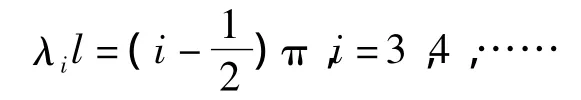
懸臂梁的各階固有頻率相應為［4］:

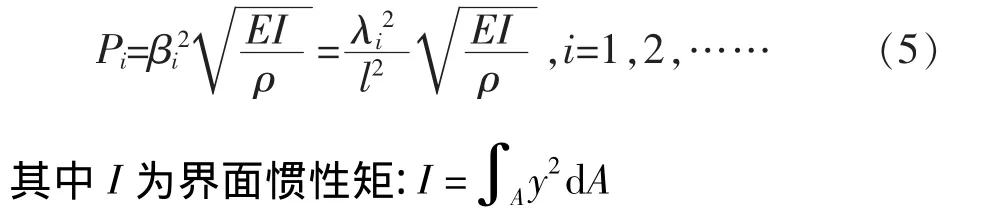
從公式(5)可以看出，對一固定材料的懸臂梁，其固有頻率主要取決于長度和橫截面慣性矩，對于總溫總壓測頭，其結構雖然與懸臂梁相似，但是還是有很大區別，如圖2所示，其各個截面根據長度不同是變化的，而且在孔的側面開有測量孔，這些都會影響到測頭的固有頻率。……