小波分析在圖像降噪中的應用

徐 健，陳士豪

（西安工程大學 電子信息學院，陜西 西安 710048）

圖像是人們通過感知器官獲取信息的主要載體之一。但是在實際的產生、傳輸和存儲的過程中都不可避免的會遭到噪聲等各種因素的影響，而這些因素會給圖像的分割、識別等處理過程帶來不必要的影響。圖像降噪可以在空間域內進行，也可以在變換域內進行。不管怎樣降噪，它們都是以噪聲和信號在頻域上的不同分布規則為依據。一般來說，有用信號是主要分布在低頻區域的，而噪聲則是大多分布在高頻區域的，然而由于圖像的細節也是分布在高頻區域的，所以如何在減少圖像噪聲的同時盡量保留圖像的細節的問題便成為了圖像降噪技術的主要研究目標[1]。

最近幾十年伴隨著小波變換在信號處理中的不斷深入研究，小波分析已經成為信號處理的有力工具，并被引入圖像處理領域處理降噪問題。正是由于其具有良好的時頻局部化特征，可以成功地去除信號中局部高頻化噪聲干擾。利用小波變換的數據壓縮特性，可以有效地消除高斯白噪聲（通常情況下，噪聲都是選用高斯白噪聲）。

1 傳統的降噪方法

傳統的圖像降噪主要有兩大類：一種是基于空間域的處理方法，另一種是基于頻域的處理方法[3]。空域內主要是在原圖像上直接進行數據運算，對像素的灰度值進行處理。變換域算法是對變換后的系數進行相應的處理，然后進行反變換從而達到圖像降噪的目的。傳統的圖像降噪多是在空域實現的。空域圖像降噪算法主要分為線性方法與非線性方法兩大類，線性方法具有比較完備的理論基礎，其中最有代表性的就是均值濾波。接下來就以均值濾波為例進行詳細介紹。

均值濾波的原理是：對于給定的一幅圖像 f（x，y），圖像中的每一個像素點（x，y），降噪后的圖像 g（x，y），降噪后的圖像中的每一個像素的灰度級由包含（x，y）鄰域的幾個像素的灰度級的平均值所決定。也就是說，用某一像素鄰域內各像素的灰度平均值來代替該像素原來的灰度值，所用的公式如下所示：

公式中的 x，y=0，1，2……，N-1；w 是以點（x，y）為中心的鄰域的集合，M是w內坐標的總數。圖像鄰域平均法的處理效果與所用的鄰域半徑有關系，半徑越大，圖像的模糊程度也越大。此外，圖像鄰域平均法算法簡單，計算速度快，但它的主要缺點是在降低噪聲的同時使圖像產生模糊，特別在邊緣和細節處，鄰域越大，模糊越厲害。

從實現難易程度上看，線性平滑濾波器比較容易實現，在信號頻譜和噪聲頻譜具有顯著不同特征時，表現出較好的性能。然而，在實際的圖像處理過程中，線性濾波器也不能完全去除脈沖噪聲。因此在許多應用場合，選用中值濾波來解決這些問題。

2 小波降噪

近年來，小波分析理論得到了非常迅速的發展，由于其具備良好的時頻特性和多分辨率特性，小波分析理論成功在許多領域得到了廣泛的應用，現在小波分析理論已經滲透到自然科學、應用科學、社會科學等領域[2]。小波降噪實際上是尋找從實際信號空間到小波函數空間的最佳映射，從而得到原信號的最佳恢復。小波降噪是一個信號濾波的問題，而且盡管在很大程度上小波降噪可以看成是低通濾波，但是由于在降噪后，還能成功地保留圖像特征，所以在這一點上優于傳統的低通濾波器。由此可見，小波降噪實際上是特征提取和低通濾波功能的綜合，其原理框圖如下：

圖1 小波分解原理圖Fig.1 The principle diagram of the wavelet decomposition

由上圖可知，尋求基于小波變換的降噪噪聲最佳方法的過程，實際上也是尋求最佳的小波變換系數處理方法的過程。

小波分析用于降噪的過程，可以細分為如下幾段：

1）分解過程。首先選擇合適的小波分析和分解層次（記為N），然后對待分析的二維圖像信號X進行N層分解計算。

2）作用閾值過程。對于分解的每一層，選擇一個合適的閾值，并對該層高頻系數進行軟閾值量化處理。在此，閾值選擇規則同前面的信號處理部分。

3）重建過程。根據小波分解后的第N層近似（低頻系數）和經過閾值量化處理后的各層細節（高頻系數），來計算二維信號的小波重構。

根據對小波系數處理方式的不同，常見的降噪方法可以分為3類：模極大值檢測法、小波系數相關降噪法和閾值降噪法。由于閾值降噪法實現簡單，計算量小，因此在實際中有著廣泛的應用[4]。所以，在此小波降噪就以閾值降噪為例詳細介紹。小波閾值降噪方法是一種實現簡單且效果較好的降噪方法。閾值降噪方法的思想很簡單。假設一個疊加了高斯白噪聲的圖像信號為：

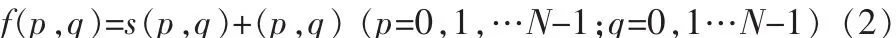
其中，s（p，q）為原始信圖像；n（p，q）為均值為 0，方差為δ2的高斯白噪聲，服從 N（0，δ2）、f（p，q）為含噪聲圖像。小波變換具有很強的數據相關性，它能夠使信號的能量集中在一些大的小波系數中，但是噪聲的能量卻分布在整個小波域內。因此，經過小波分解后，信號的小波系數幅值要大于噪聲的系數幅值。幅值相對比較大的小波系數一般以信號為主，而幅值比較小的系數在很大程度上是噪聲。采用閾值的辦法設置一個合適的閾值對于大于該閾值的小波系數予以保留，小于該閾值的小波系數（主要成分是噪聲）予以剔除，這樣就能使大部分噪聲系數減小至零，從而達到降噪的目的。

圖2 小波閾值降噪原理圖Fig.2 The principle diagram of wavelet threshold de-noising

小波閾值降噪方法的一個關鍵因素是閾值的選取，另一個關鍵因素是閾值的估計[5]。如果閾值太小降噪后的圖像仍然存在噪聲，如果閾值太大，重要圖像特征又將被濾掉，引起偏差。從直觀上講，對給定的小波系數，噪聲越大，閾值就越大。

小波閾值降噪的基本思想是：首先對含有噪聲的信號做小波變換，得到一組小波系數；接著對其進行閾值處理，得到估計系數，使得兩者的差值盡可能小；最后利用小波重構，得到估計信號即為降噪的信號。

閾值處理的方法有兩種：一種是硬閾值法，定義為

硬閾值法得到的小波系數的連續性較差，重構信號可能出現突變或者震蕩現象；如下圖所示。另一種方法是軟閾值法，定義為：

軟閾值法得到的小波系數的連續性好，但是當小波系數比較大時得到處理后的小波系數和實際的小波系數有一定的偏差，會導致重構結果的誤差。如圖3所示。

圖3 兩種閾值方法Fig.3 Two threshold methods

3 改進的算法介紹

設X是大小為原始無噪圖像，是一個在空間平穩、獨立同分布、方差為δ2的零均值高斯白噪聲，Y是一個被噪聲污染的含噪圖像。噪聲滿足一下關系：

小波變換把圖像信號變換到小波域，在小波域中，圖像本身的能量主要分布在低分辨率的尺度系數和一些較大的小波系數上，而噪聲能量仍然均勻散布在低分辨率的尺度系數和所有小波系數上[6]。在變換域，圖像的空間相關性降低，能量更加集中，而噪聲的能量分布情況則不變。根據以上情況我們提出了一種基于小波閾值的混合濾波圖像降噪的方法。其步驟為：

1）對含有噪聲圖像進行小波分解；

2）對小波分解系數進行閾值處理；

3）對處理后的系數重構；

4）對重構圖像進行均值濾波。

4 實驗結果與分析

為說明該方法的有效性，對含有高斯白噪聲的一幅風景的圖像進行降噪處理，其中噪聲方差δ2為10。在降噪實驗中，采用“sym4”小波，因為sym小波有較好的對成性，更適合于圖像處理，減少重構時的相移[7]。有較好的對稱性的小波濾波器既可以使人類的視覺系統對邊緣附近對稱的量化誤差較非對稱誤差更不敏感，又具有線性相位特性。對圖像邊緣作對稱邊界擴展時，重構圖像邊緣部分失真較小，如圖4所示。

圖4 不同算法的圖像降噪比較Fig.4 Comparison of image noise reduction of different algorithms

表1 不同噪聲大小、不同方法降噪后的PSNR結果Tab.1 PSNR results of different sizes and methods for noise reduction

由表1可以看出本算法能夠較好地去除噪聲，且降噪后圖像清晰、明了，有較好的視覺效果，足以說明以閾值降噪為基礎的混合算法的優越性。

5 結束語

小波降噪已經應用于許多理論和領域，其在信號處理過程中的作用使其成為信號處理研究的熱點。文中介紹了傳統降噪方法與小波降噪方法的優缺點，并基于兩類方法的不同特點，提出了一種基于小波閾值的混合濾波圖像降噪[8]的新方法。仿真實驗表明：該算法對圖像降噪保留了較多的細節信息，使降噪后的圖像在主觀視覺效果方面得到了明顯的改善；對含有高斯白噪聲的圖像，可以較為清晰地恢復出原始圖像，從而驗證了該算法的實用價值。

[1]夏良正.數字圖像處理[M].東南大學出版社，1999：89-96.

[2]成禮智，王紅霞，羅永.小波的理論與應用[M]．北京：科學出版社，2004．

［3］盛仲飆．基于Matlab的圖像去噪算法研究［J］．河南科學，2011，29（10）：1218-1220．CHENG Zhong-biao.Image denoising algorithm based on Matlab research[J].Journal of Henan Science，2011，29（10）:1218-1220.

[4]廖福元，黃國石．兩種小波閾值去噪算法的比較研究[J].計算機工程與應用，2004，16：101-103．LIAO Fuyuan，HUANG Guo-shi.Two kinds of comparative study of wavelet threshold denoising algorithm[J].Computer engineering and application，2004:101-103.

[5]潘泉，戴冠中，張洪才．基于閾值決策的子波域去噪方法[J]．電子學報，1998，26（1）：115-117.PAN Quan，DAI Guan-zhong， ZHANG Hong-cai.Decisions based on threshold wavelet domain denoising method[J].Journal of Electronics，1998，26（1）:115-117.

[6]Kenneth R.Castleman著數字圖像處理[M].朱志剛，等譯.數字圖像處理.電子工業出版社，2002．

[7]董長虹.小波分析工具箱原理與應用[M].北京：國防工業出版社，2004.

[8]韓長材，宋顧周，馬繼明，等.科學級CCD相機噪聲標定及特性分析[J].現代應用物理，2014（3）：233-238.HAN Geng-cai，SONG Gu-zhou，MA Ji-ming，et al.Noise calibration and characterization of scientific grade CCD camera[J].Modern Applied Physics，2014（3）：233-238.